Michael Bronstein은 대수적 토폴로지를 활용하여 새로운 그래프 신경망 컴퓨팅 구조를 제안합니다!
이 기사는 Cristian Bodnar 및 Fabrizio Frasca가 공동 집필했으며 C. Bodnar, F. Frasca 등이 2021 ICML "Weisfeiler and Lehman Go Topological: Information Transfer Simple Network" 및 2021 NeurIPS "Weisfeiler and Lehman Go"에 게재했습니다. 셀룰러: CW 네트워크" 》논문은 참고용입니다.
이 글은 미분기하학과 대수적 위상수학의 관점에서 본 그래프 신경망 시리즈에 대한 논의의 일부일 뿐입니다.
그래프는 컴퓨터 네트워크부터 대형 강입자 충돌기의 입자 상호 작용까지 모든 것을 시뮬레이션하는 데 사용할 수 있습니다. 그래프는 불연속적이고 조합적인 특성으로 인해 어디에나 존재하며, 이를 통해 계산하기 쉬우면서도 추상적인 관계를 표현할 수 있습니다. 인기 있는 이유 중 하나는 그래프가 기하학적 구조(예: 노드가 공간에 있는 위치 또는 가장자리가 어떻게 구부러지는지)를 추상화하고 노드가 어떻게 연결되어 있는지에 대한 표현만 남기기 때문입니다.
그래프 이론은 Leonhard Euler가 1741년 저서 "Geometria situs"에서 유명한 Königsberg Seven Bridges 문제에 대한 해결책이 없다는 관찰에서 유래되었습니다.
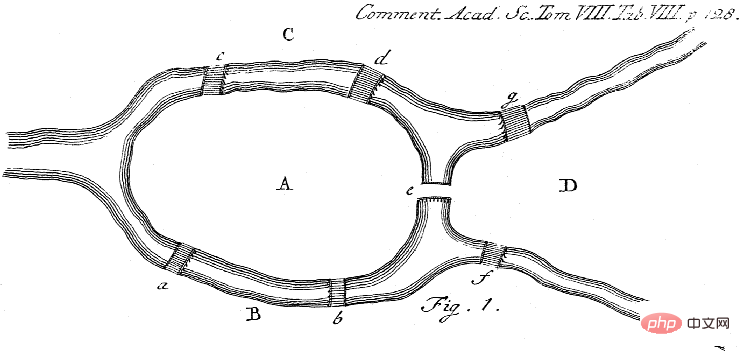
그림: 7개의 다리 문제는 다리를 여러 번 건너지 않고 Königsberg 시에서 원형 도보 경로를 찾는 것입니다. 오일러가 말했듯이, 쾨니히스베르크 시의 정확한 모양은 중요하지 않습니다. 중요한 것은 서로 다른 토지(그래프의 노드)가 어떻게 서로 연결되어 있는지(모서리)입니다. 오일러는 모든 노드가 짝수 차수를 갖는 경우에만 그러한 순환이 존재한다는 것을 보여주었습니다. 또한 원래의 다리 중 5개만이 현대까지 남아 있습니다. 출처: Wikipedia
흥미롭게도 오일러의 발견은 그래프 이론의 시작일 뿐만 아니라 종종 위상수학의 탄생으로 간주되기도 합니다. 그래프와 마찬가지로 위상학자는 특정 모양이나 기하학적 구조와 무관한 공간의 속성에 관심이 있습니다.
이러한 아이디어의 현대적 표현은 1895년 Henri Poincaré의 주요 논문인 "Analytic situs"에 나타났습니다. 그의 작업은 다양체의 조합 설명에 대한 관심을 불러일으켰습니다. 위상 불변량은 이러한 다양체에서 더 쉽게 찾고 계산할 수 있습니다. .
그림: Leonhard Euler(1707-1783) 및 Henri Poincaré(1854-1912)
이러한 결합된 설명은 오늘날 세포 복합체라고 불리며 더 높은 차원의 그래프 일반화로 생각할 수 있습니다.
노드와 모서리로 구성된 그래프와 달리 셀 복합체는 더 높은 차원 구조 또는 "셀"을 포함할 수도 있습니다. 정점은 0-셀, 가장자리는 1-셀, 2D 표면은 2-셀 등입니다. 세포 복합체를 구축하려면 한 세포의 경계를 다른 저차원 세포에 접착하여 층을 이룰 수 있습니다.
특별한 경우, 세포가 단순체(예: 모서리, 삼각형, 사면체 등)로 구성되는 경우 이러한 공간을 단순 복합체라고도 합니다.

캡션: 그래프는 모서리(1셀)를 연결하는 정점 집합으로 볼 수 있습니다. 마찬가지로 단일 세포 복합체와 세포 복합체는 2세포(파란색), 3세포(녹색) 등을 연결한 그래프로 볼 수 있습니다.
1 기계 학습 및 데이터 과학의 토폴로지
우리는 토폴로지가 실용적인 도구가 되기까지 400년을 기다릴 필요가 없다고 믿습니다.
얕은 복합체와 같은 위상 구조는 위상 데이터 분석(TDA)이라는 이름 아래 기계 학습 및 데이터 과학에 사용되어 왔습니다. 이러한 유형의 방법은 둔감하고 잡음에 강한 방식을 측정하려는 시도로 1990년대에 등장했습니다. "데이터의 형태"를 분석합니다.
TDA의 뿌리는 1920년대 후반 가장 활발한 토폴로지 학자 중 한 명인 Leopold Vietnam Oris의 작업으로 거슬러 올라갑니다. 그러나 이러한 기술이 대규모로 적용되기 위해서는 현대 컴퓨팅이 출현할 때까지 기다려야 했습니다.

범례: 점 구름이 주어지면 각 점 주위의 고정 반경의 닫힌 구 사이의 교차점은 단순한 복합체를 생성합니다. 구의 반경을 점진적으로 증가시키면 단순 복합체의 중첩된 시퀀스를 얻을 수 있습니다. 이미지 출처: Bastian Rieck.
TDA의 핵심은 포인트 클라우드에서 위상적 특징을 추출하는 방법인 영구 상동성(PH)입니다. 점 데이터 세트가 주어지면 PH는 단순 복소수의 중첩된 시퀀스를 생성합니다. 여기서 각 복소수는 분석 중인 기본 점 구름의 특정 규모에 해당합니다. 그런 다음 규모가 점차 증가하고 시퀀스의 한 복합체에서 다음 복합체로 전환됨에 따라 나타나고 사라지는 다양한 토폴로지 특징(예: 연결된 구성 요소, 루프 또는 구멍)을 추적합니다.
딥러닝 시대에 지속적 상동성은 이를 통해 역전파를 수행할 수 있으며 이미 확립된 TDA 장치를 딥러닝 프레임워크에 통합할 수 있음이 입증되면서 "제2의 삶"을 갖게 되었습니다.
최근 연구에서는 수행되는 데이터와 계산을 지원하는 보다 풍부한 기본 토폴로지 공간으로서 기하학적 딥 러닝에서 단순화와 셀 복합체의 다양한 용도를 제안합니다.
이 관점을 활용한 초기 작업 중 일부는 단순화된 단지에서 작동하는 컨벌루션 모델과 랜덤 워크 방법을 제안했습니다. 이 글에서처럼 컨벌루션 모델은 세포 복합체에 대한 정보 전달의 간단하고 구체적인 예로 이해될 수 있습니다.
계산은 이러한 공간의 위상학적 구조(즉, 이웃 구조)에 의해 구동되므로 이 방법을 위상학적 정보 전송이라고 부릅니다. 이 프레임워크에서는 아래 그림에 표시된 것처럼 서로 다른 차원의 인접한 장치가 정보를 교환하고 있습니다.
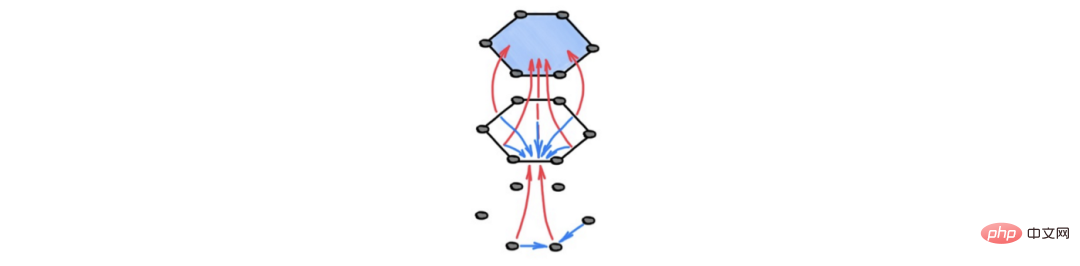
캡션: 위상 정보 전송의 개략도. 파란색 화살표는 상위 계층의 인접한 셀, 즉 동일한 고차원 셀의 경계에 있는 셀 간의 "수평" 정보 전파를 나타냅니다. 빨간색 화살표는 셀이 경계에 있는 낮은 차원 셀로부터 정보를 받는 "수직" 정보 전파를 나타냅니다. 이 계산은 경계 셀의 정보를 더 거친 표현으로 요약하여 (미분 가능한) 앙상블 형식으로 해석될 수 있습니다.
GNN의 그래프 너머
세포 복합체가 제공하는 풍부한 구조에도 불구하고 우리는 그래프가 기계 학습에서 가장 일반적인 토폴로지 개체이며 그래프를 능가하는 데이터 세트가 거의 없다는 점을 무시할 수 없습니다. 그럼에도 불구하고 입력 그래프를 변환하여 이러한 흥미로운 위상 공간을 활용할 수 있습니다.
범주론의 동명의 개념과 유사하게 그래프를 고차원 위상 공간으로 변환하는 것을 "리프팅"이라고 부릅니다. 특정 규칙에 따라 입력 그래프에 고차원 셀을 추가하는 변환입니다. 예를 들어, 그래프의 각 절벽이나 주기에 더 높은 차원의 셀을 부착하여 그래프를 셀 복합체로 승격시킬 수 있습니다. 이를 통해 그래프는 더 많은 구조를 갖고 원래 그래프보다 더 나은 계산 구조를 GNN에 제공할 수 있는 다른 공간으로 대체됩니다. 아래에서는 이 접근 방식의 구체적인 장점에 대해 설명합니다.
캡션: 2차원 폐쇄 원판의 경계를 그래프의 유도된 루프에 붙이면 그래프에서 고차원 세포 복합체를 구성할 수 있습니다.
고차 기능 및 구조
GNN은 일반적으로 노드 중심 보기를 채택하며 가장자리에 있는 데이터는 꼭지점 간 통신을 늘리기 위해 보조 정보로만 간주됩니다. 토폴로지 정보 전송에서 모든 단위는 일류 시민입니다. 치수에 관계없이 이웃 단위와 정보를 교환하여 개발되는 특정 표현이 할당됩니다. 이는 특정 고차 구조와 이들 간의 상호 작용을 명시적으로 모델링하기 위한 방법을 제공합니다. 특히, 이는 대규모 GNN 모델 클래스에서는 고려하지 않는 문제인 입력 그래프의 에지(즉, 1 단위) 기능을 발전시키기 위한 원칙적인 접근 방식을 제공합니다.
고차 상호 작용
다이어그램은 정의상 이진("쌍별")이며 두 개 이상의 개체와 관련된 관계 및 상호 작용을 나타낼 수 없습니다. 이는 고차 상호작용을 특징으로 하는 복잡한 시스템을 모델링할 때 문제가 될 수 있습니다. 예를 들어 화학 반응에서 세 개의 반응물이 동시에 상호작용할 수 있습니다. 셀 복합체에서 이러한 상황은 두 셀(즉, "채워진" 삼각형) 사이의 반응물을 연결하여 인코딩될 수 있습니다. 따라서 모델의 계산 흐름은 고차 상호 작용의 존재에 맞게 조정됩니다.
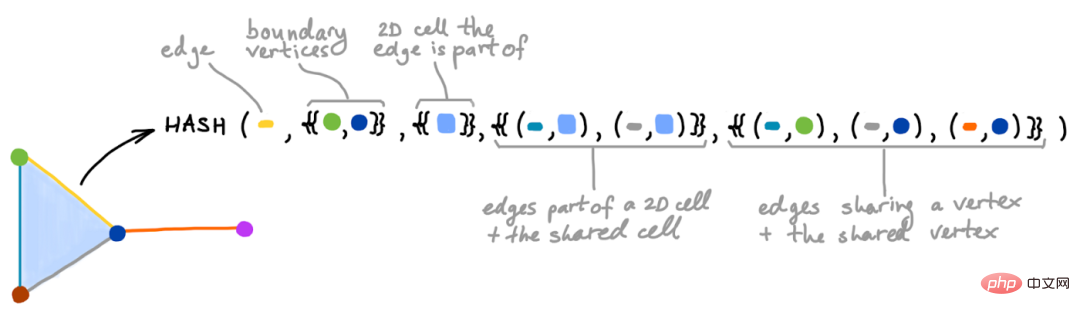
캡션: CWL(Cell Weisfeiler-Lehman) 테스트는 기존 WL 테스트를 세포 모집단으로 확장하며, 알고리즘의 각 단계는 인접한 셀의 색상을 완벽하게 해시합니다(다양한 차원이 있을 수 있음).
표현력
정보 전송 GNN의 표현력은 Weisfeiler-Leman(WL) 그래프 동형성 테스트에 의해 제한됩니다. WL은 매우 단순한 비구조도 삼각형이나 순환과 같은 특정 그래프 하위 구조를 감지할 수 없는 것으로 알려져 있습니다. - 동형 이미지도 구별이 불가능합니다.
이전 논문에 따르면 (논문 주소: https://arxiv.org/abs/2103.03212; https://arxiv.org/abs/2106.12575), WL 테스트(CWL) 버전은 세포 복합체의 동형성을 테스트하는 데 사용될 수 있습니다. 이 새로운 테스트를 위에서 설명한 그래프 리프팅 절차와 일치시키면 WL 테스트보다 더 큰 그래프 클래스를 구분할 수 있음을 알 수 있습니다. 따라서 특정 조건에서 위상 정보 전송 프로세스는 이 테스트의 장점을 계승하고 표준 GNN에 비해 표현 능력을 향상시킵니다. 부적절하고 과도한 스무딩 및 병목 현상
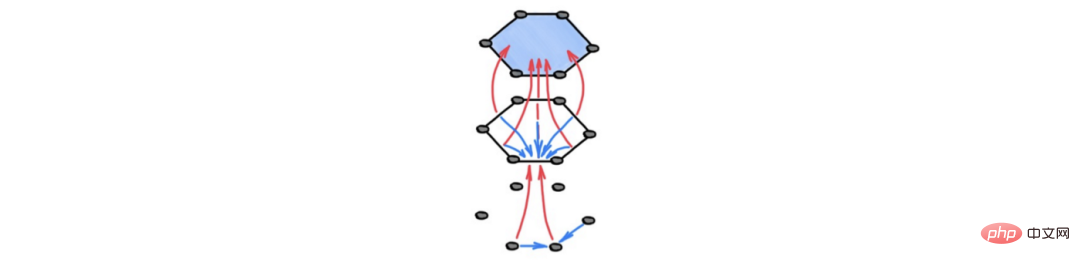
정보 전송을 위한 GNN은 n 홉 떨어져 있는 노드가 통신할 수 있도록 n 레이어가 필요합니다. 몇 개의 레이어만 사용하여 멀리 떨어져 있는 노드가정보를 교환할 수 없는 경우 이러한 현상을 언더리치라고 합니다.
반대로 레이어를 너무 많이 사용하면 지나치게 평활화될 수 있으며 그래프의 구조적 병목 현상으로 인해 정보가 손실될 수 있습니다.고차원 유닛에 의해 유도된 보다 풍부한 동네 구조가 멀리 떨어져 있을 수 있는 노드 사이에 지름길을 만들기 때문에 유닛 단지는 이러한 문제를 완화할 수 있습니다. 따라서 정보에는 일부 계산 단계만 포함하면 유효하게 전파될 수 있습니다.
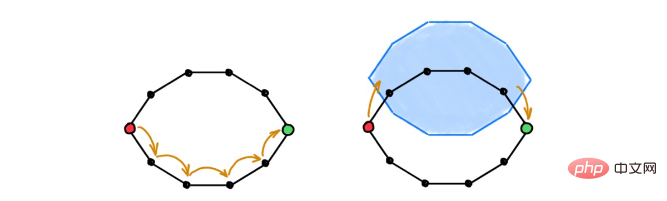
캡션: GNN은 멀리 떨어져 있는 노드가 통신할 수 있도록 많은 레이어가 필요합니다(왼쪽). 고차원 셀은 지름길을 만들어 공간의 기본 토폴로지를 변경합니다(오른쪽). 이를 통해 원격 노드는 여러 메시징 단계에서 정보를 교환할 수 있습니다. Hierarchical Modeling
TopologyInformation정보 전달에 의해 수행되는 계산은 계층적이며, 정보는 저차원 단위에서 고차원 단위로, 그리고 그 반대로 흐르며, 이는 "수직"(및 미분 가능)으로 간주될 수 있습니다. ) 풀 표준 그래프 신경망의 "수평" 풀링 대신 풀링 형태입니다. 이는 GNN 풀링 기반 성능에 해를 끼칠 수 있는 입력 그래프의 세밀한 정보를 무시하지 않고 "압축된" 그래프 영역의 유도적 편향을 유지합니다.
캡션: 위상 정보 전송을 통해 서로 다른 차원의 단위 간에 정보가 계층적으로 존재할 수 있습니다.
도메인 정렬
특정 응용 프로그램은 자연적으로 원자, 결합 및 화학 고리와 같은 세포 복합체의 구조와 일치합니다. 0-셀, 1-셀 및 2-셀로 표시됩니다. 분자의 물리적 구조와 셀의 복잡한 표현 사이의 직접적인 대응으로 인해 위상 정보 전달이 위의 특성을 활용할 수 있습니다. 정보 전달은 분자 특성 예측 작업에서 최첨단 결과를 달성합니다.
좋은 정렬을 보이는 다른 애플리케이션에는 컴퓨터 그래픽 애플리케이션의 개별 다양체(그리드), 소셜 네트워크(파벌이 특히 중요함) 또는 Google 지도와 같은 공간 그래프(거리 사이의 블록이 자연스럽게 나타날 수 있음)가 포함될 수 있습니다. "큐빅" 셀).
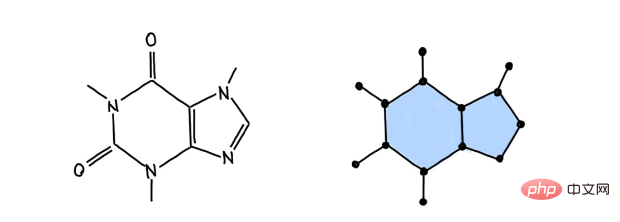
캡션: 커피 인자는 2차원 세포 복합체로 모델링됩니다
2 위상수학과 미분 기하학의 결합
정공 대수 및 방향 등가
대수 위상수학에서는 방향성 단순 복소수를 사용하는 것이 일반적입니다. 여기서 각 단체에 대한 임의의 "방향"이 있습니다. 예를 들어 소스 노드와 대상 노드를 선택하고 각 삼각형의 노드를 순회하는 순서를 선택합니다. 방향이 선택되면 "경계 연산자"를 통해 특정 단체의 경계를 계산하는 등 복잡한 모양에 대해 흥미로운 대수 연산자를 수행할 수 있습니다. 이러한 대수적 연산은 경계가 없지만 다른 것의 경계에 있지 않은 영역인 단순 복합체에서 "구멍"을 찾는 데에도 사용할 수 있습니다. 배후에서 지속적인 상동성은 이러한 계산에 의존하여 토폴로지 특징을 감지합니다.
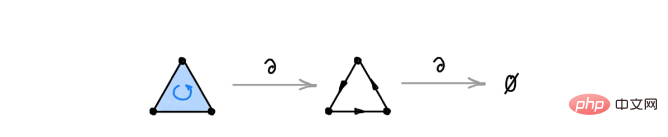
캡션: 2-심플렉스에 적용된 경계 연산자는 삼각형을 생성합니다. 삼각형에 연산자를 다시 적용하면 결과는 0입니다. 삼각형은 경계가 없는 순환이기 때문입니다.
위상 정보 전송은 대수 연산자(예: 경계 연산자)의 (비선형) 일반화로 볼 수 있습니다. 따라서 위상 정보 전달이 유사하게 동작해야 합니다. 즉, 각 레이어의 출력이 입력 복합체의 방향 변화에 "균일하게" 반응하기를 원합니다. 즉, 우리는 레이어가 방향적으로 동일해지기를 원합니다. 우리 연구에서는 적절한 비선형성과정보 전달 함수를 선택하여 위상학적 정보 전달이 이 속성을 어떻게 충족하는지 연구하고, 이는 순전히 컨벌루션 설정에서도 연구됩니다. 위상 공간 구별최초의 알려진 위상 불변 중 하나인 오일러 서명은 원래 플라톤 다면체의 분류에 사용되었으며, 이는 각 차원에 있는 셀 수의 교대 합으로 정의할 수 있습니다. 놀랍게도 두 세포 복합체가 동형인 경우 동일한 공간을 서로 다르게 이산화하더라도 이러한 합은 일관됩니다.
흥미롭게도 위상 정보 전달 모델의 판독 연산은 각 차원 단위에 포함 불변량의 감소를 적용하기 때문에 위상의 불변성을 쉽게 계산할 수 있습니다.따라서 이러한 유형의 모델은 특정 비동형 공간(즉, 다른 오일러 특성을 가짐)을 구조적으로 구별할 수 있습니다. 계산적 관점에서 볼 때 이는 WL 테스트의 일반화로 볼 수 있습니다. 여기서 우리는 두 세포 복합체가 동일한지 여부뿐만 아니라 서로 동형인지 여부를 결정하는 데 관심이 있습니다.
이산 호지 이론은 세포 복합체의 위상학적 특성에 대해 보다 기하학적인 설명을 제공합니다. k-셀과 관련된 특징의 부호가 k-셀의 방향에 따라 달라질 때 이러한 특징은 미분 기하학에서 미분 k-모양의 이산 버전으로 수학적으로 볼 수 있습니다(즉, k-차원 볼륨 요소는 다음과 같습니다. 통합) . Hoch Laplacian이라고 불리는 연산자는 그래픽 라플라시안을 일반화하고 이러한 미분 형태로 작동합니다. 이 라플라시안 연산자를 기반으로 한 확산 PDE는 합성물의 홀과 관련된 신호에 한계 내에서 수렴할 것임을 증명할 수 있습니다. 범례: Hoch Laplace 연산자를 기반으로 한 확산 편미분 방정식은 Laplace 연산자 코어의 초기 미분 형식 투영 한계에 수렴합니다. 이 이미지는 Hoch Laplacian의 0 고유 벡터가 복합체의 구멍 주변에서 어떻게 높은 값을 취하는지 보여줍니다. 최초의 단순 신경망 모델은 실제로 Hoch Laplace의 컨벌루션 모델을 기반으로 했으며 이는 위상적 신호 처리에서 영감을 받았습니다. 최근에는 이 연산자를 기반으로 한 컨벌루션 모델 버전이 계산 대수 토폴로지의 NP 하드 문제를 해결하는 데 사용되었습니다. 최근 논문에서는 무엇보다도 위상학적 정보 전달 방법이 세포 복합체의 구조를 인코딩하는 수정된 그래프에서 정보 전달을 수행하는 GNN에 지나지 않는다고 주장합니다. 이는 정보 전달 계산에 셀 쌍이 포함되는 컨벌루션 모델의 경우에도 마찬가지입니다. 그러나 가장 일반적인 형태에서 정보 정보 기능을 사용하면 고차원 셀이 경계의 하위 차원 셀 간에 전달되는 정보 정보를 변조할 수 있습니다. 일반적으로 그래프의 일반 메시지를 통해 정보를 전송할 수 있습니다. 하나의 모서리는 정확히 두 개의 노드를 연결하고 2셀은 원하는 수의 모서리를 연결할 수 있기 때문입니다. 토폴로지 정보 전달의 다음 단계는 무엇인가요?
첫째, 수년에 걸쳐 GNN에서 개발된 많은 아키텍처(예: 주의 메커니즘)가 이러한 새로운 토폴로지 공간에서 채택될 수 있습니다. 특정 특성. 두 번째로 대수 토폴로지 분야의 더 많은 수학적 개체 및 도구(가장 수학에 정통한 ML 연구자에게도 낯설게 들릴 수 있는 벌집 도르래와 같은 구조 포함)는 그래프 및 기하학적 딥 러닝 커뮤니티에서 채택됩니다. . 이산 호지 이론
위 내용은 Michael Bronstein은 대수적 토폴로지를 활용하여 새로운 그래프 신경망 컴퓨팅 구조를 제안합니다!의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)
 CUDA의 보편적인 행렬 곱셈: 입문부터 숙련까지!
Mar 25, 2024 pm 12:30 PM
CUDA의 보편적인 행렬 곱셈: 입문부터 숙련까지!
Mar 25, 2024 pm 12:30 PM
GEMM(일반 행렬 곱셈)은 많은 응용 프로그램과 알고리즘의 중요한 부분이며 컴퓨터 하드웨어 성능을 평가하는 중요한 지표 중 하나이기도 합니다. GEMM 구현에 대한 심층적인 연구와 최적화는 고성능 컴퓨팅과 소프트웨어와 하드웨어 시스템 간의 관계를 더 잘 이해하는 데 도움이 될 수 있습니다. 컴퓨터 과학에서 GEMM의 효과적인 최적화는 컴퓨팅 속도를 높이고 리소스를 절약할 수 있으며, 이는 컴퓨터 시스템의 전반적인 성능을 향상시키는 데 중요합니다. GEMM의 작동 원리와 최적화 방법에 대한 심층적인 이해는 현대 컴퓨팅 하드웨어의 잠재력을 더 잘 활용하고 다양하고 복잡한 컴퓨팅 작업에 대한 보다 효율적인 솔루션을 제공하는 데 도움이 될 것입니다. GEMM의 성능을 최적화하여
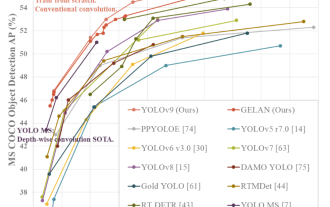 YOLO는 불멸이다! YOLOv9 출시: 성능과 속도 SOTA~
Feb 26, 2024 am 11:31 AM
YOLO는 불멸이다! YOLOv9 출시: 성능과 속도 SOTA~
Feb 26, 2024 am 11:31 AM
오늘날의 딥러닝 방법은 모델의 예측 결과가 실제 상황에 가장 가깝도록 가장 적합한 목적 함수를 설계하는 데 중점을 두고 있습니다. 동시에 예측을 위한 충분한 정보를 얻을 수 있도록 적합한 아키텍처를 설계해야 합니다. 기존 방법은 입력 데이터가 레이어별 특징 추출 및 공간 변환을 거치면 많은 양의 정보가 손실된다는 사실을 무시합니다. 이 글에서는 딥 네트워크를 통해 데이터를 전송할 때 중요한 문제, 즉 정보 병목 현상과 가역 기능을 살펴보겠습니다. 이를 바탕으로 다중 목표를 달성하기 위해 심층 네트워크에서 요구되는 다양한 변화에 대처하기 위해 PGI(Programmable Gradient Information) 개념을 제안합니다. PGI는 목적 함수를 계산하기 위해 대상 작업에 대한 완전한 입력 정보를 제공할 수 있으므로 네트워크 가중치를 업데이트하기 위한 신뢰할 수 있는 기울기 정보를 얻을 수 있습니다. 또한 새로운 경량 네트워크 프레임워크가 설계되었습니다.
 워드 문서에서 덧셈, 뺄셈, 곱셈, 나눗셈을 계산하는 방법
Mar 19, 2024 pm 08:13 PM
워드 문서에서 덧셈, 뺄셈, 곱셈, 나눗셈을 계산하는 방법
Mar 19, 2024 pm 08:13 PM
WORD는 워드를 사용하여 다양한 텍스트를 편집할 수 있는 강력한 워드 프로세서입니다. Excel 표에서는 덧셈, 뺄셈, 승수 계산 방법을 익혔습니다. 따라서 Word 표에서 숫자의 덧셈을 계산해야 한다면, 승수를 빼는 방법은 계산기로만 계산할 수 있나요? 대답은 물론 '아니요'입니다. WORD도 그렇게 할 수 있습니다. 오늘은 Word 문서에서 수식을 사용하여 표의 덧셈, 뺄셈, 곱셈, 나눗셈 등의 기본 연산을 계산하는 방법을 함께 배워보겠습니다. 그럼 오늘은 WORD 문서에서 덧셈, 뺄셈, 곱셈, 나눗셈을 계산하는 방법을 자세히 보여드리겠습니다. 1단계: WORD를 열고 툴바의 [삽입] 아래 [표]를 클릭한 후 드롭다운 메뉴에 표를 삽입합니다.
 Python의 count() 함수를 사용하여 목록의 요소 수를 계산하는 방법
Nov 18, 2023 pm 02:53 PM
Python의 count() 함수를 사용하여 목록의 요소 수를 계산하는 방법
Nov 18, 2023 pm 02:53 PM
Python의 count() 함수를 사용하여 목록의 요소 수를 계산하려면 특정 코드 예제가 필요합니다. 강력하고 배우기 쉬운 프로그래밍 언어인 Python은 다양한 데이터 구조를 처리하기 위한 많은 내장 함수를 제공합니다. 그 중 하나는 목록의 요소 수를 계산하는 데 사용할 수 있는 count() 함수입니다. 이번 글에서는 count() 함수의 사용법을 자세히 설명하고 구체적인 코드 예시를 제공하겠습니다. count() 함수는 Python의 내장 함수로, 특정 값을 계산하는 데 사용됩니다.
 Java에서 부분 문자열의 발생 횟수를 재귀적으로 계산합니다.
Sep 17, 2023 pm 07:49 PM
Java에서 부분 문자열의 발생 횟수를 재귀적으로 계산합니다.
Sep 17, 2023 pm 07:49 PM
두 개의 문자열 str_1과 str_2가 주어졌습니다. 목표는 재귀 프로시저를 사용하여 문자열 str1에서 하위 문자열 str2의 발생 횟수를 계산하는 것입니다. 재귀 함수는 정의 내에서 자신을 호출하는 함수입니다. str1이 "Iknowthatyouknowthatiknow"이고 str2가 "know"인 경우 발생 횟수는 -3입니다. 예를 들어 str1="TPisTPareTPamTP", str2="TP"를 입력하면 Countofoccurrencesofasubstringrecursi가 출력됩니다.
 행렬식을 사용하여 삼각형의 면적을 계산하는 Java 프로그램
Aug 31, 2023 am 10:17 AM
행렬식을 사용하여 삼각형의 면적을 계산하는 Java 프로그램
Aug 31, 2023 am 10:17 AM
소개 행렬식을 이용하여 삼각형의 면적을 계산하는 자바 프로그램은 세 꼭지점의 좌표를 주어 삼각형의 면적을 계산할 수 있는 간결하고 효율적인 프로그램이다. 이 프로그램은 Java에서 기본 산술 및 대수 계산을 사용하는 방법과 Scanner 클래스를 사용하여 사용자 입력을 읽는 방법을 보여주기 때문에 기하학을 배우거나 작업하는 모든 사람에게 유용합니다. 프로그램은 사용자에게 삼각형의 세 점 좌표를 묻는 메시지를 표시하고 이를 읽어 좌표 행렬의 행렬식을 계산하는 데 사용합니다. 행렬식의 절대값을 사용하여 면적이 항상 양수인지 확인한 다음 공식을 사용하여 삼각형의 면적을 계산하여 사용자에게 표시합니다. 이 프로그램은 다양한 형식의 입력을 받아들이거나 추가 계산을 수행하도록 쉽게 수정할 수 있으므로 기하학적 계산을 위한 다용도 도구가 됩니다. 행렬식의 순위
 1.3ms는 1.3ms가 걸립니다! Tsinghua의 최신 오픈 소스 모바일 신경망 아키텍처 RepViT
Mar 11, 2024 pm 12:07 PM
1.3ms는 1.3ms가 걸립니다! Tsinghua의 최신 오픈 소스 모바일 신경망 아키텍처 RepViT
Mar 11, 2024 pm 12:07 PM
논문 주소: https://arxiv.org/abs/2307.09283 코드 주소: https://github.com/THU-MIG/RepViTRepViT는 모바일 ViT 아키텍처에서 잘 작동하며 상당한 이점을 보여줍니다. 다음으로, 본 연구의 기여를 살펴보겠습니다. 기사에서는 경량 ViT가 일반적으로 시각적 작업에서 경량 CNN보다 더 나은 성능을 발휘한다고 언급했는데, 그 이유는 주로 모델이 전역 표현을 학습할 수 있는 MSHA(Multi-Head Self-Attention 모듈) 때문입니다. 그러나 경량 ViT와 경량 CNN 간의 아키텍처 차이점은 완전히 연구되지 않았습니다. 본 연구에서 저자는 경량 ViT를 효과적인
 C#에서 Math.Pow 함수를 사용하여 지정된 숫자의 거듭제곱을 계산하는 방법
Nov 18, 2023 am 11:32 AM
C#에서 Math.Pow 함수를 사용하여 지정된 숫자의 거듭제곱을 계산하는 방법
Nov 18, 2023 am 11:32 AM
C#에는 많은 수학 함수가 포함된 Math 클래스 라이브러리가 있습니다. 여기에는 지정된 숫자의 거듭제곱을 계산하는 데 도움이 되는 거듭제곱을 계산하는 Math.Pow 함수가 포함됩니다. Math.Pow 함수의 사용법은 매우 간단합니다. 밑수와 지수만 지정하면 됩니다. 구문은 다음과 같습니다. Math.Pow(base,expont); 여기서 base는 밑수를 나타내고 지수는 지수를 나타냅니다. 이 함수는 double형 결과, 즉 거듭제곱 계산 결과를 반환합니다. 하자






