딥러닝의 토폴로지 미학: GNN 기초 및 적용

소개: 현실 세계에서는 소셜 네트워크, 전자상거래 쇼핑, 단백질 상호작용 관계 등 많은 데이터가 그래프 형태로 나타나는 경우가 많습니다. 최근 몇 년간 그래프 데이터 분석 및 신경망 기반의 마이닝 방법은 뛰어난 성능으로 폭넓은 주목을 받았으며, 학계의 연구 핫스팟이 되었을 뿐만 아니라 다양한 응용 분야에서 빛을 발하고 있습니다. 이 글은 주로 관련 문헌, 해당 분야 전문가들의 공유, 저자의 피상적인 경험을 결합하여 대략적인 요약과 귀납을 이룬다. 지식의 전달이기는 하지만 개인적인 주관적 판단이 섞여 있기도 하므로 주의하시기 바랍니다. 새해에는 모든 분들이 바라는 일 모두 이루시고, 평안하시고 행복하시길 기원합니다.
1. 그래프 신경망 개발 개요

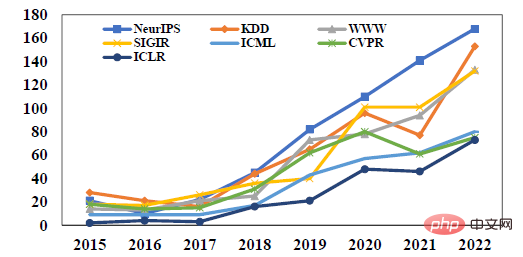
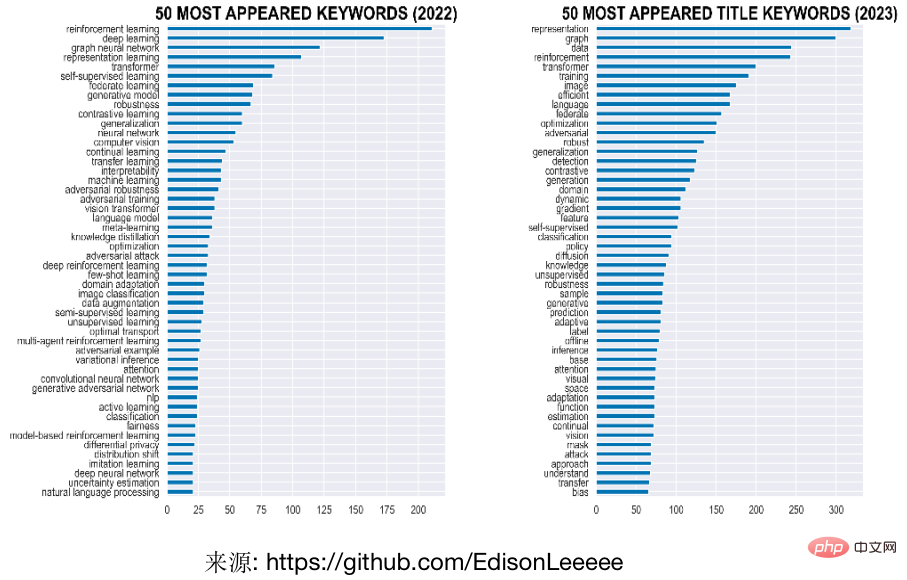
최근 몇 년 동안 모델링을 활용하여 그래프 구조를 분석하는 연구가 점점 더 주목을 받고 있습니다. 그 중 딥러닝 그래프 모델링 방법을 기반으로 한 GNN(Graph Neural Network)은 뛰어난 성능으로 인해 주목을 받고 있습니다. 학계의 연구 핫스팟 중 하나가 됩니다. 예를 들어, 아래 그림에서 볼 수 있듯이 머신러닝 관련 주요 학회에서 그래프 신경망에 관한 논문 수가 계속해서 늘어나고 있습니다. 그래프를 제목이나 키워드로 사용하는 것은 최고의 학회인 ICLR에서 가장 인기 있는 단어 중 하나였습니다. 지난 2년간의 표현 학습. 이 밖에도 그래프 신경망은 올해 여러 학회의 최우수 논문상에도 등장한 바 있다. 일례로 데이터마이닝의 최고 학회인 KDD의 최우수 박사학위 논문 1, 2위는 그래프 관련 젊은 학자 2명에게 돌아갔다. 머신러닝 최고의 연구 논문과 응용 논문은 각각 하이퍼그래프와 연합 그래프 학습에 대한 인과 학습에 관한 것입니다. 한편, 그래프 신경망은 전자상거래 검색, 추천, 온라인 광고, 금융 위험 관리, 교통 예측 및 기타 분야에서도 많은 실용적인 응용 프로그램을 보유하고 있습니다. 주요 기업들도 그래프 학습 관련 플랫폼이나 기능을 구축하기 위해 열심히 노력하고 있습니다.
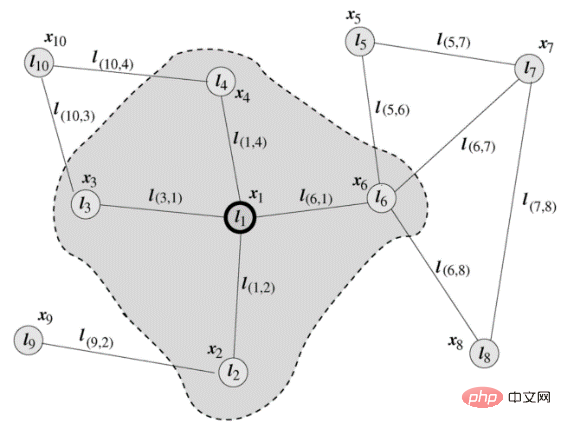
그래프 신경망은 지난 5년 동안 연구의 중심이 되었지만 관련 정의는 2005년 이탈리아 학자 Marco Gori와 Franco Scarselli가 제안했습니다. Scarselli의 논문에 있는 일반적인 다이어그램은 다음과 같습니다. GNN의 초기 단계에서는 주로 RNN을 기본 프레임워크로 사용하고 노드 이웃 정보를 입력하여 노드 상태를 업데이트하고 로컬 전달 함수를 순환 재귀 함수로 정의합니다. 각 노드는 주변 이웃 노드와 연결된 가장자리를 소스 정보로 사용하여 업데이트합니다. 자신의 익스프레스.
LeCun의 학생 Bruna 등은 2014년에 CNN을 그래프에 적용할 것을 제안했습니다. 그들은 컨볼루션 연산자의 영리한 변환을 통해 주파수 영역과 공간 영역 기반 그래프 컨볼루션 네트워크를 기반으로 하는 두 가지 정보 집계 방법을 제안했습니다. 스펙트럼 기반 방법은 그래프 신호 처리 관점에서 필터를 도입하여 그래프 컨벌루션을 정의합니다. 여기서 그래프 컨벌루션 작업은 그래프 신호에서 노이즈를 제거하는 것으로 해석됩니다. 공간 기반 방법은 CNN 패러다임과 더 일치하며 이웃의 특징 정보를 집계하여 그래프 컨볼루션을 나타냅니다. 그 후 몇 년 동안 일부 새로운 모델이 산발적으로 제안되었지만 여전히 상대적으로 틈새 연구 방향이었습니다. 2017년이 되어서야 그래프 모델 삼총사인 GCN, GAT, GraphSage로 대표되는 일련의 연구 작업이 제안되어 그래프 데이터와 컨볼루션 신경망 사이의 계산 장벽이 열리면서 그래프 신경망이 점차 연구 핫스팟으로 메시지 전달 메커니즘(MPNN)을 기반으로 하는 그래프 신경망 모델의 현재 기본 패러다임의 기반을 마련했습니다.
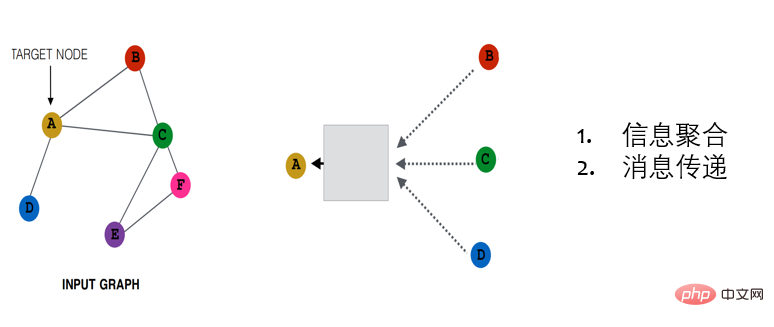
일반적인 MPNN 아키텍처는 여러 전파 계층으로 구성되며, 이웃 특성의 집계 기능을 기반으로 각 노드를 업데이트합니다. 다양한 집계 함수에 따라 MPNN은 다음과 같이 나눌 수 있습니다. 정보 집계(이웃 특성의 선형 조합, 가중치는 GCN과 같은 그래프 구조에만 의존함), 어텐션(선형 조합, 가중치는 그래프 구조에 따라 다름) GAT와 같은 기능) 및 메시지 전달(GraphSAGE와 같은 일반화된 비선형 함수)은 아래 그림의 왼쪽에서 오른쪽으로 표시됩니다.
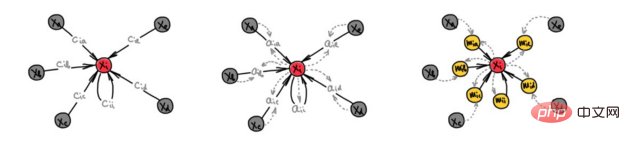
추론의 관점에서는 전달적(예: GCN)과 귀납적(예: GraphSage)으로 나눌 수도 있습니다. 직접 푸시 방법은 각 노드에 대한 고유한 표현을 학습하지만 이 모델의 한계는 업계 대부분의 비즈니스 시나리오에서 그래프의 구조와 노드를 새로 변경할 수 없다는 점입니다. 사용자는 계속해서 사용자 컬렉션에 나타날 것이며 사용자의 관심 관계 컬렉션도 계속해서 성장할 것이며 매일 콘텐츠 플랫폼에 수많은 새로운 기사가 추가될 것입니다. 이러한 시나리오에서 직접 푸시 학습에는 새 노드에 대한 표현을 학습하기 위한 지속적인 재교육이 필요합니다. 귀납적 방법은 노드 이웃 특성의 "집합 함수"를 학습하는 것으로, 이는 새로운 노드의 표현이나 그래프 구조의 변화와 같은 보다 유연한 시나리오에 적용할 수 있으므로 다양한 그래프에 적용할 수 있습니다. 실제 시나리오는 역동적으로 변화합니다.
그래프 신경망 개발 과정에서 그래프 네트워크 계산의 정확성과 확장성 문제를 해결하기 위해 새로운 모델이 세대를 거쳐 끊임없이 제안되고 있습니다. 그래프 데이터를 표현하는 그래프 신경망의 능력은 의심의 여지가 없지만 새로운 모델 설계는 주로 경험적 직관, 경험적 방법 및 실험적 시행착오 방법을 기반으로 합니다. Jure Leskovec 그룹의 2019년 관련 연구 GIN(Graph Isomorphism Networks)은 그래프 동형 검출을 위해 GNN과 고전적인 휴리스틱 알고리즘 Weisfeiler Lehman(WL) 간의 연결을 확립했으며 GNN의 표현 능력의 상한이 1-WL임을 이론적으로 증명했습니다(Jure는 현재 스탠포드대학교 컴퓨터공학부 부교수로 재직하고 있으며, 그가 이끄는 SNAP 연구실은 현재 그래프 네트워크 분야에서 가장 유명한 연구실 중 하나로, 그가 강의하고 있는 CS224W '그래프 머신 러닝(Graph Machine Learning)'은 적극 추천하는 학습이다. 재료). 그러나 WL 알고리즘은 아래 그림의 두 가지 예와 같이 많은 데이터 시나리오에 대해 표현 기능이 매우 제한되어 있습니다. (a)의 CSL(Circular Skip Link) 그래프의 경우 1-WL은 두 그래프의 각 노드를 동일한 색상으로 표시합니다. 즉, 완전히 다른 구조를 가진 두 그래프입니다. 테스트하려면 1-WL을 사용하세요. 우리는 같은 라벨을 얻게 될 것입니다. 두 번째 예는 (b)에 표시된 데칼린 분자입니다. 1-WL은 a와 b를 같은 색으로 염색하고, c와 d를 같은 색으로 염색하므로 연결 예측 작업에서 (a, d)와 ( b, d) 구별할 수 없습니다.
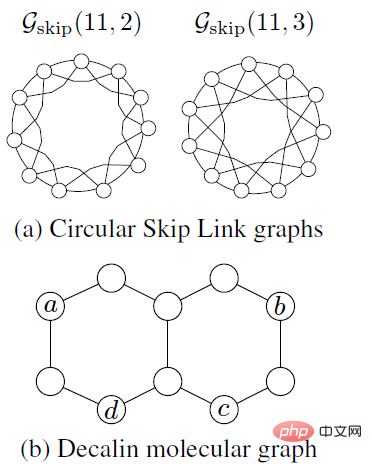
WL-테스트는 삼각형 또는 고리형 구조를 가진 많은 데이터에서 만족스럽지 못한 결과를 보여줍니다. 그러나 생화학과 같은 분야에서는 고리형 구조가 매우 일반적이며 분자의 해당 특성을 결정하므로 그래프의 응용 가능성도 매우 높습니다. 관련 시나리오의 네트워크는 크게 제한됩니다. Micheal Bostein 등은 현재의 그래프 딥러닝 방법의 '노드 중심과 에지 중심' 사고 방식이 큰 한계를 가지고 있다고 제안했습니다. 이를 바탕으로 그래프 학습의 발전과 가능한 새로운 접근 방식을 관점에서 재고할 것을 제안했습니다. 패러다임(Micheal은 현재 옥스퍼드 대학의 DeepMind 인공 지능 교수이자 트위터 그래프 학습 연구 그룹의 수석 과학자이자 기하학적 딥 러닝의 발기인 중 한 명입니다.) 또한 많은 학자들이 미분 기하학, 대수 위상학 및 미분 방정식 분야의 일련의 새로운 도구에 대한 연구를 시작했으며 등변 그래프 신경망, 위상 그래프 신경망, 하위 그래프 신경망 등과 같은 일련의 작업을 제안했습니다. 많은 문제를 해결하여 눈길을 끄는 결과를 얻었습니다. 그래프 신경망의 개발 맥락과 결합하면 아래와 같이 간단하게 요약할 수 있습니다.

2. 복잡한 그래프 모델
이전 섹션에서 언급된 해당 그래프 신경망은 기본적으로 무방향 및 동종 그래프를 기반으로 설정되었습니다. 그러나 현실 세계의 그래프는 복잡한 경우가 많습니다. 연구자들은 방향성 그래프, 이종 그래프, 동적 그래프, 하이퍼그래프, 부호 있는 그래프 및 기타 시나리오에 대한 그래프 신경망 모델을 각각 제안했습니다. 그래프 데이터 형식 및 관련 모델:
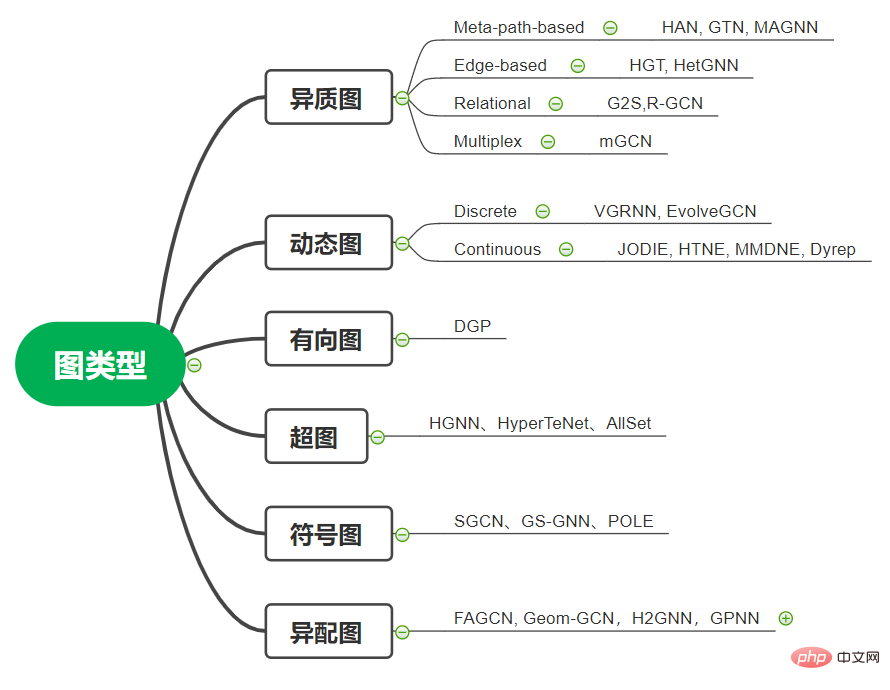
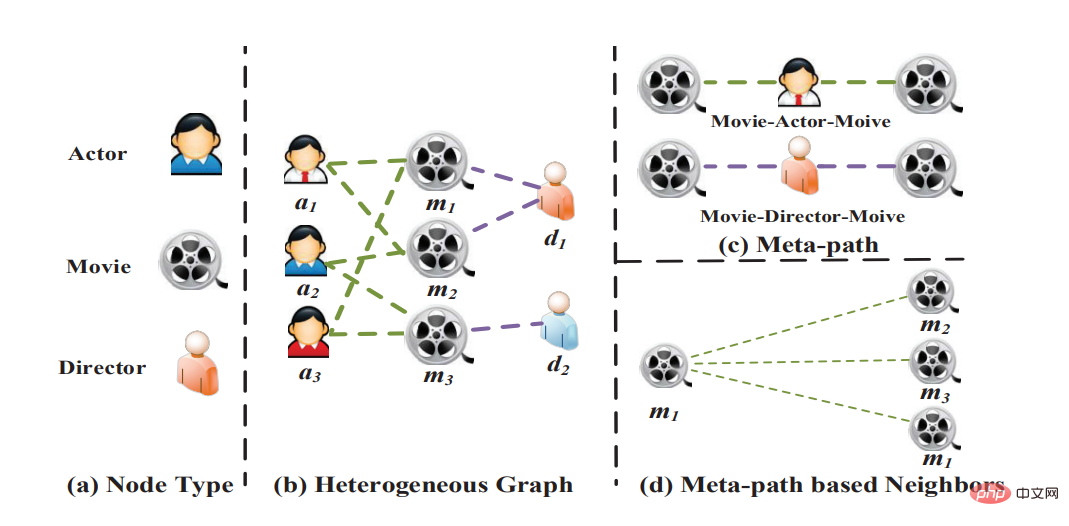
1. 이종 그래프: 이종 그래프는 노드와 가장자리에 여러 범주가 있고 여러 모델이 있음을 의미합니다. 예를 들어 전자상거래 시나리오에서 노드는 제품, 매장, 사용자 등이 될 수 있고 에지 유형은 클릭, 컬렉션, 거래 등이 될 수 있습니다. 구체적으로, 이종 그래프에서 각 노드는 유형 정보를 전달하고, 각 에지도 유형 정보를 전달합니다. 공통 GNN 모델은 해당 이종 정보를 모델링할 수 없습니다. 한편으로는 다양한 유형의 노드의 임베딩 차원을 정렬할 수 없습니다. 반면에 다양한 유형의 노드의 임베딩은 서로 다른 의미 공간에 위치합니다. 이종 그래프에 대해 가장 널리 사용되는 학습 방법은 메타 경로 기반 방법입니다. 메타패스는 경로의 각 위치에서 노드 유형을 지정합니다. 학습 중에 메타 경로는 노드 시퀀스로 인스턴스화되며, 메타 경로 인스턴스의 양쪽 끝에 있는 노드를 연결하여 직접 연결될 수 없는 두 노드의 유사성을 캡처합니다. 이러한 방식으로 이종 그래프를 여러 개의 동형 그래프로 축소할 수 있으며, 이러한 동형 그래프에 그래프 학습 알고리즘을 적용할 수 있습니다. 또한 일부 연구에서는 서로 다른 이웃 노드와 에지에 대해 서로 다른 샘플링 기능과 집계 기능을 사용하는 이종 그래프를 처리하기 위한 에지 기반 방법을 제안했습니다. 대표작으로는 HetGNN, HGT 등이 있습니다. 때때로 관계 그래프를 처리해야 하는 경우도 있습니다. 이러한 그래프의 가장자리에는 카테고리 이외의 정보가 포함되어 있거나 가장자리 카테고리의 수가 너무 많아 메타 경로나 메타 관계 기반 방법을 사용하기 어려울 수 있습니다. 이종 그래프에 관심이 있는 친구들은 북경대학교 이시카와 선생님과 왕샤오 선생님의 일련의 작업을 따라갈 수 있습니다.
2. 동적 그래프: 동적 그래프는 시간이 지남에 따라 노드와 토폴로지 구조가 변화하는 그래프 데이터를 말하며 실제 시나리오에서도 널리 사용됩니다. 예를 들어, 학술 인용 네트워크는 시간이 지남에 따라 계속 확장될 것이고, 사용자와 제품 간의 상호 작용 그래프는 사용자 관심에 따라 변화할 것이며, 교통 네트워크와 교통 흐름은 시간이 지남에 따라 계속 변화할 것입니다. 동적 그래프의 GNN 모델은 주어진 시간에 노드 표현을 생성하는 것을 목표로 합니다. 시간 세분성의 두께에 따라 동적 그래프는 이산 시간 동적 그래프(스냅샷 기반이라고도 함)와 연속 시간 동적 그래프(이벤트 기반)로 나눌 수 있으며 이산 시간 동적 그래프에서는 시간이 여러 시간으로 나뉩니다. 조각(예: 일/시간으로 구분), 각 시간 조각은 정적 그림에 해당합니다. 이산시간 동적 그래프의 GNN 모델은 일반적으로 각 타임 슬라이스에 별도로 GNN 모델을 적용한 다음 RNN을 사용하여 서로 다른 시간의 노드 표현을 집계합니다. 대표적인 작업으로는 DCRNN, STGCN, DGNN, EvolveGCN 등이 있습니다. 연속시간 동적 그래프에서 각 가장자리에는 상호작용 이벤트가 발생하는 순간을 나타내는 타임스탬프가 첨부됩니다. 정적 그래프와 비교하여 연속시간 동적 그래프의 메시지 기능은 주어진 샘플의 타임스탬프와 에지의 타임스탬프에 따라 달라집니다. 또한, 이웃 노드는 시간과 관련이 있어야 합니다. 예를 들어 특정 시간 이후에 나타나는 노드는 이웃 노드에 나타날 수 없습니다. 모델 관점에서 볼 때, 연속 동적 그래프를 모델링하는 데 포인트 프로세스가 자주 사용됩니다. 이웃 생성 시퀀스의 조건부 강도 함수를 최적화하여 시퀀스의 도달률을 생성하는 방법으로 이벤트가 발생하는 특정 순간을 추가로 예측할 수도 있습니다. (예: 네트워크의 특정 링크가 종료되는 시간) 연속 동적 그래프 모델링에 대한 대표적인 작품으로는 JODIE, HTNE, MMDNE, Dyrep 등이 있습니다.
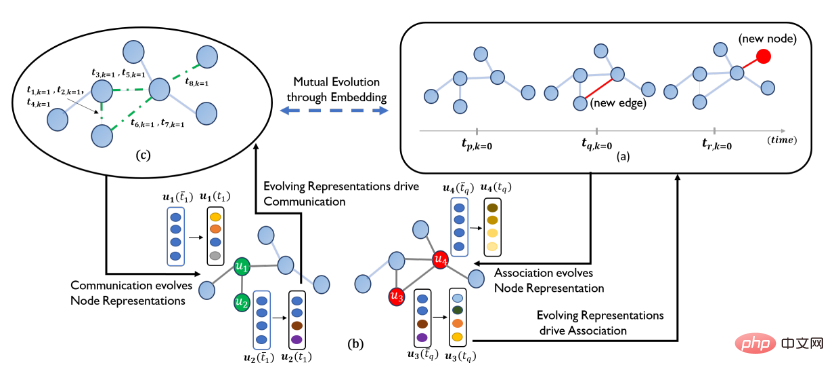
출처: Dyrep
3. 하이퍼그래프: 하이퍼그래프는 넓은 의미의 그래프이며, 그 모서리 중 하나는 모든 정점을 연결할 수 있습니다. 수량. 하이퍼그래프에 대한 연구 초기에는 주로 컴퓨터 비전 시나리오에 대한 응용과 관련이 있었지만 최근에는 그래프 신경망 분야에서도 주목을 받고 있습니다. 그래프의 노드 수는 다양한 유형의 여러 가장자리를 통해 전달될 수 있습니다. 다양한 유형의 간선을 활용하여 그래프를 여러 레이어로 구성할 수 있으며, 각 레이어는 관계 유형을 나타냅니다. 대표작으로는 HGNN, AllSet 등이 있습니다.
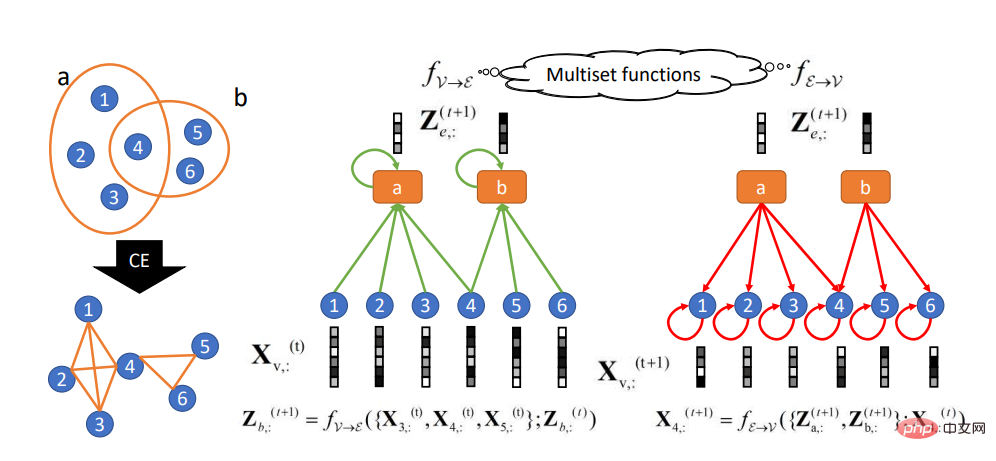
출처: AllSet
4. 방향성 그래프: 방향성 그래프는 노드의 연결 관계가 방향성이 있다는 것을 의미하며 방향성이 있는 가장자리는 종종 방향이 없는 가장자리보다 더 많은 정보를 포함합니다. 예를 들어, 지식 그래프에서 머리 엔터티가 꼬리 엔터티의 상위 클래스인 경우 가장자리의 방향은 이 부분 순서 관계에 대한 정보를 제공합니다. 방향성 그래프 시나리오의 경우 단순히 컨볼루션 연산에서 비대칭 인접 행렬을 사용하는 것 외에도 더 나은 표현을 얻기 위해 가장자리의 두 방향을 별도로 모델링할 수도 있습니다. 대표적인 작품으로는 DGP 등이 있습니다.
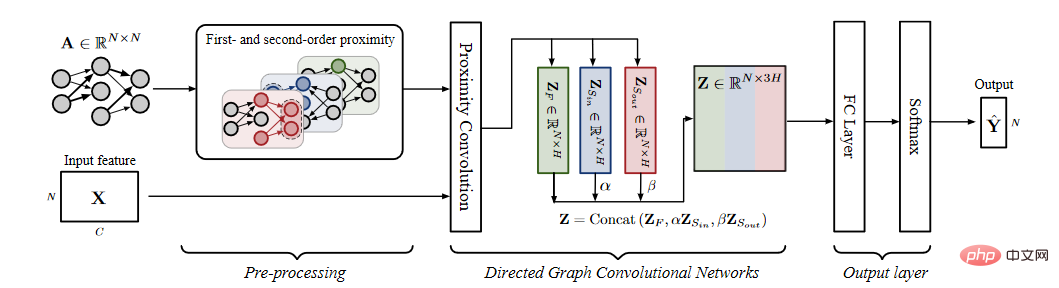
출처: DGP
5. 서명된 그래프: 서명된 그래프는 소셜 네트워크와 같은 정방향 및 역방향 관계를 포함하여 그래프 내 노드 간의 관계를 나타냅니다. 기호 그래프에는 우정, 동의, 지지와 같은 긍정적인 관계뿐만 아니라 적, 불일치, 저항 등과 같은 부정적인 관계도 포함됩니다. 기호 그래프는 일반 그래프에 비해 더 풍부한 노드 상호 작용 관계를 포함합니다. 기호 그래프를 모델링할 때 해결해야 할 주요 문제는 음의 간선을 모델링하는 방법과 두 가지 유형의 간선 정보를 집계하는 방법입니다. SGCN은 균형 이론(친구의 친구는 친구이고 적의 친구는 동일)의 가정을 기반으로 합니다. 적) 해당 평형 경로를 정의하여 해당 모델링을 수행합니다. 또한 대표적인 연구로는 기호 네트워크를 사용한 편파 임베딩 모델 POLE, 이분 기호 그래프 신경망 모델 SBGNN, k-그룹 이론을 기반으로 한 기호 그래프 신경망 GS-GNN 등이 있습니다.
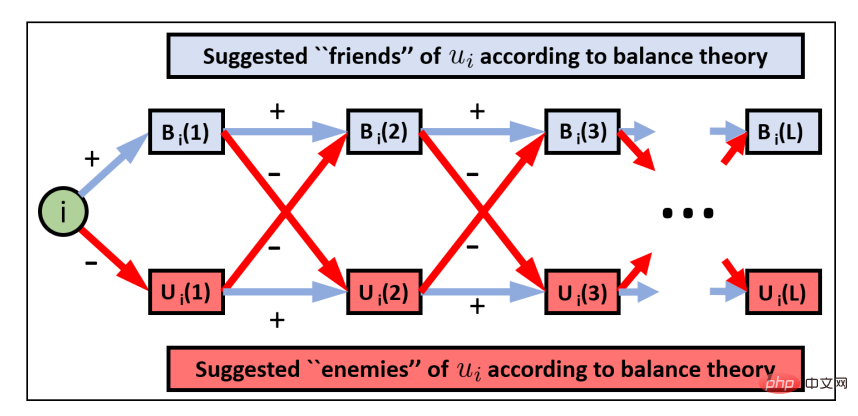
출처: SGCN
6. 불일치 그래프: 위의 다른 유형의 그래프와 정의가 약간 다릅니다. 이종성 그래프(heterophy graph)라고 불리는 것은 그래프에서 이웃 노드의 유사성이 상대적으로 낮은 데이터 유형을 의미합니다. 이형혼에 대응되는 것은 동형혼입니다. 이는 연결된 노드가 일반적으로 동일한 범주에 속하거나 유사한 특성을 가짐을 의미합니다("깃털이 있는 새들이 함께 모인다"). 예를 들어, 친구의 정치적 신념이나 나이가 비슷할 수도 있고, 논문이 같은 연구 분야의 논문을 인용하는 경향이 있을 수도 있습니다. 그러나 실제 네트워크는 높은 동질성 가정을 완전히 준수하지 않습니다. 예를 들어 단백질 분자에서는 다양한 유형의 아미노산이 서로 연결되어 있습니다. 그래프 신경망 집계 및 링크 관계를 통한 특징 전파의 메커니즘은 동종 데이터의 가정을 기반으로 하기 때문에 GNN은 종종 이질성이 높은 데이터에 대해 좋지 않은 결과를 얻습니다. 현재 구조적 정보를 사용해 노드의 이웃을 선택하는 모델인 Geom-GCN, 그래프 신경망의 표현력을 향상시켜 그래프 신경망의 표현력을 향상시키는 H2GNN 등 그래프 신경망을 이종 그래프 시나리오로 일반화하려는 많은 작업이 있었습니다. 메시지 전달 메커니즘, 중앙 노드 상관 재정렬(아래 그림에 표시된 것처럼 서로 다른 색상은 서로 다른 노드 유형을 나타냄)을 기반으로 정보 수집을 위한 포인터 네트워크 GPNN을 구축하고, 고주파 신호와 저주파 신호 처리를 동시에 결합하여 FAGCN, 등.
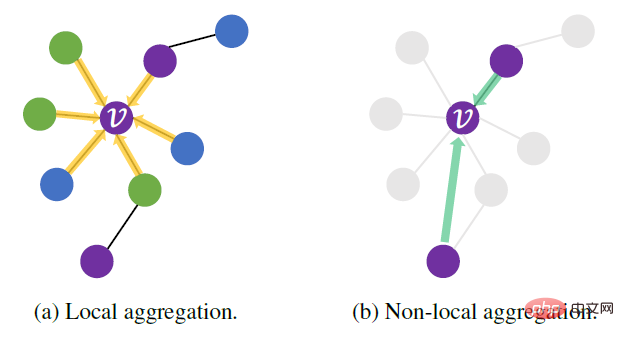
출처: GPNN
3. 그래프 신경망 응용
그래프 신경망은 그래프 구조 데이터의 특성을 더 잘 학습할 수 있으므로 그래프와 관련된 많은 분야에서 폭넓게 응용됩니다. 응용과 탐구. 이 섹션에서는 다운스트림 작업 및 애플리케이션의 관점에서 그에 따라 분류하고 요약합니다.
1. 다운스트림 작업
노드 분류: 노드의 속성에 따라(카테고리 가능) 유형 또는 숫자 유형) , 가장자리 정보, 가장자리 속성(있는 경우), 알려진 노드 예측 레이블, 알 수 없는 레이블이 있는 노드에 대한 범주 예측. 예를 들어, OGB의 ogbn-products 데이터 세트는 방향이 지정되지 않은 제품 구매 네트워크입니다. 노드는 전자 상거래에서 판매되는 제품을 나타냅니다. 두 제품 사이의 가장자리는 해당 제품이 함께 구매되었음을 나타냅니다. 설명에서 Bag-of-Word 특징을 추출한 다음 주성분 분석을 수행하여 차원 축소를 생성합니다. 해당 작업은 상품의 누락된 카테고리 정보를 예측하는 것입니다.
링크 예측: 네트워크에서의 링크 예측은 알려진 네트워크 노드 및 네트워크 가능성 등의 정보를 통해 아직 엣지를 생성하지 않은 네트워크 내 두 노드 간의 링크를 예측하는 방법을 말합니다. 이 예측에는 알려지지 않은 링크에 대한 예측과 향후 링크에 대한 예측이 모두 포함됩니다. 링크 예측은 추천 시스템, 생화학 실험 및 기타 시나리오에서 널리 사용됩니다. 예를 들어 제품 추천에서 사용자와 제품의 이분 그래프에서 사용자가 제품을 구매하면 사용자와 제품 사이에 링크가 있고, 유사한 사용자가 동일한 상품을 가질 수 있으므로 해당 상품에 대한 수요가 있을 것입니다. 따라서 해당 사용자와 상품 사이에 '구매', '클릭' 등의 링크가 발생할 가능성이 있는지 예측하여 타겟화된 방식으로 사용자에게 상품을 추천합니다. , 제품의 구매율을 높일 수 있습니다. 또한, 자연어 처리에서의 지식 그래프 완성, 스마트 교통에서의 교통 예측 등도 링크예측 문제로 모델링할 수 있다.
그래프 분류: 그래프 분류는 실제로 노드 분류와 유사합니다. 핵심은 그래프의 레이블을 예측하는 것입니다. 그래프의 특성(예: 그래프 밀도, 그래프 토폴로지 정보 등)과 알려진 그래프의 레이블을 기반으로 알 수 없는 레이블이 있는 그래프에 대한 카테고리 예측을 만드는 것은 훈련 그래프 신경과 같은 생물정보학 및 화학 정보학에서 찾을 수 있습니다. 단백질 구조를 예측하는 네트워크.
그래프 생성: 그래프 생성의 목표는 새로운 분자 구조 생성을 기반으로 한 생물학적 정보나 자연어 처리 등 관찰된 그래프 집합을 바탕으로 새로운 그래프를 생성하는 것입니다. 의미 그래프 또는 주어진 문장을 기반으로 한 지식 그래프입니다.
2. 적용 분야
따라서 다양한 적용 시나리오를 소개하겠습니다.

추천 시스템: 모바일 인터넷의 발전은 정보 검색의 급속한 발전을 크게 촉진했습니다. 추천 시스템은 가장 중요한 방향으로 널리 주목을 받았습니다. 추천 시스템의 주요 목적은 과거의 상호 작용과 부가 정보로부터 효과적인 사용자 및 항목 표현을 학습하여 사용자가 선호할 가능성이 높은 항목(상품, 음악), 비디오, 영화 등을 추천하는 것입니다. 따라서 추천 효과를 향상시키기 위해 그래프 신경망을 추천 시스템에 적용할 수 있도록 항목과 사용자를 노드로 하는 이분 그래프를 구성하는 것을 고려하는 것이 당연합니다. 핀터레스트는 GraphSAGE를 기반으로 30억 개의 노드와 180억 개의 엣지로 대규모 이미지 추천 시나리오를 지원하는 GCN 기반 최초의 산업 수준 추천 시스템인 핀세이지를 제안했습니다. 실제로 온라인에 접속한 후 핀터레스트의 Shop and Look 제품 조회수가 증가했습니다. 또한 Alibaba, Amazon 및 기타 여러 전자상거래 플랫폼에서는 GNN을 사용하여 해당 추천 알고리즘을 구축합니다.

사용자-항목 상호 작용으로 구성된 이분 그래프 외에도 추천 시스템의 사회적 관계와 지식 그래프 시퀀스의 항목 전달 그래프가 모두 그래프 데이터 형식으로 존재합니다. 한편, 이질성 구조 데이터는 추천 시스템의 전자상거래 시나리오에서도 널리 사용됩니다. 노드는 쿼리, 항목, 상점, 사용자 등이 될 수 있으며 에지 유형은 클릭, 컬렉션, 트랜잭션 등이 될 수 있습니다. 프로젝트, 사용자와 사용자, 사용자와 프로젝트 간의 관계 및 콘텐츠 정보를 활용하고, 멀티 소스 이종 및 멀티 모달 그래프 모델을 기반으로 고품질의 추천 효과도 지속적으로 탐색되고 있습니다. 또한 실제 비즈니스에서 시간에 따른 사용자 행동 변화를 기반으로 한 직렬화된 추천과 새로운 사용자 및 제품 추가로 인한 점진적인 학습도 GNN 모델 개발에 새로운 도전과 기회를 가져왔습니다.
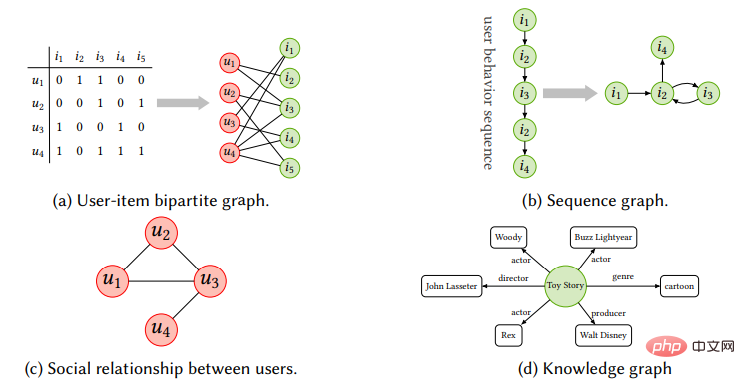
자연어 처리: 자연어 처리의 많은 문제와 시나리오는 연관 관계를 설명하므로 자연스럽게 그래프 데이터 구조로 모델링될 수 있습니다. 첫 번째 직접 적용 시나리오는 지식 그래프(KG)의 완성 및 추론입니다. 예를 들어 Mila의 연구자들은 단일 홉 추론 문제를 NBFNet 기반의 경로 표현 학습 문제로 모델링하여 귀납적 추론을 실현할 것을 제안했습니다. . 그래프 신경망은 심층 신경망을 사용하여 그래프 데이터의 위상 구조 정보와 속성 특징 정보를 통합함으로써 노드 또는 하위 구조에 대한 보다 정교한 특징 표현을 제공하고, 분리 또는 엔드 투 엔드 방식으로 다운스트림과 쉽게 통신할 수 있습니다. 엔터티와 관계의 속성 특성과 구조적 특성을 학습하기 위한 다양한 응용 시나리오의 지식 그래프 요구 사항을 충족합니다.
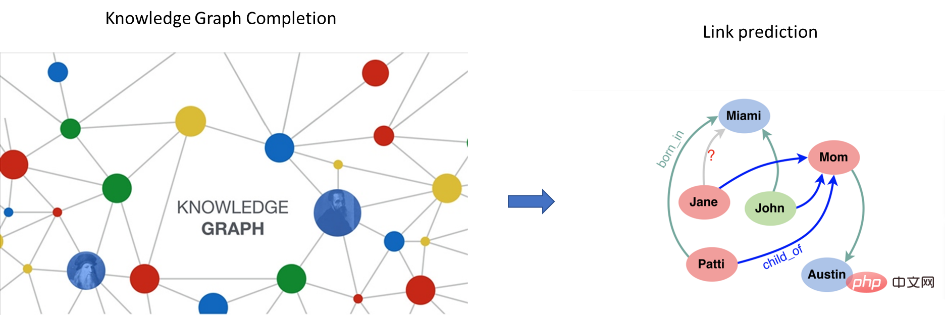
또한 그래프 신경망은 텍스트 분류, 의미 분석, 기계 번역, 지식 그래프 완성, 명명된 엔터티 인식, 기계 분류 등 자연어 처리의 많은 문제에 해당 응용 프로그램이 있습니다. Wu Lingfei 박사의 Graph4NLP 관련 튜토리얼 및 리뷰를 참조하세요.
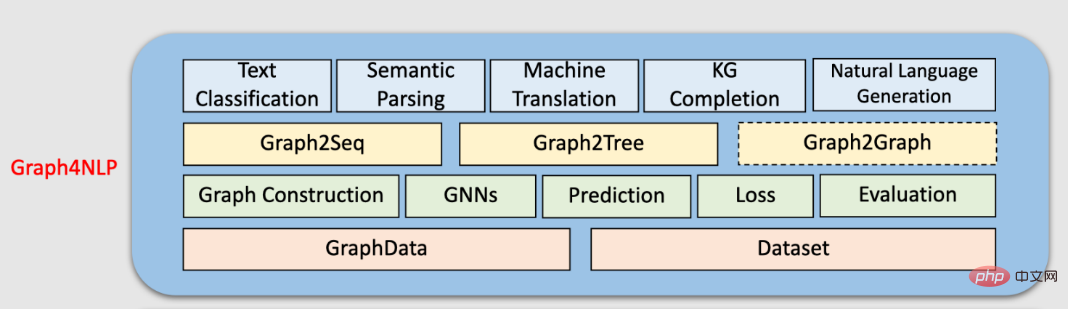
출처: (https://github.com/graph4ai/graph4nlp)
컴퓨터 비전: 컴퓨터 비전은 기계 학습 분야에서 가장 큰 응용 시나리오 중 하나입니다. 추천 시스템 및 자연어 처리 분야에 비해 딥 러닝, 그래프 신경망은 컴퓨터 비전에서 주류가 아닙니다. 그 이유는 GNN의 장점은 관계 모델링 및 학습이며, 컴퓨터 비전의 데이터 형식은 대부분 일반 이미지 데이터이기 때문입니다. CV 시나리오에서 GNN을 사용할 때 핵심은 그래프가 구성되는 방식에 있습니다. 정점과 정점 기능은 무엇입니까? 정점의 연결 관계를 어떻게 정의하나요? 초기 작업은 직관적이고 그래프 구조를 추상화하기 쉬운 일부 장면에 주로 사용됩니다. 예를 들어, 동적 골격에 사용되는 동작 인식 방법 ST-GCN에서는 인체의 자연스러운 골격을 자연스럽게 그래프 구조로 간주하여 공간 그래프를 구성할 수 있습니다. 장면 그래프 생성에서 객체 간의 의미론적 관계는 시각적 장면 뒤에 있는 의미론적 의미를 이해하는 데 도움이 됩니다. 이미지가 주어지면 장면 그래프 생성 모델은 객체를 감지 및 인식하고 객체 쌍 간의 의미론적 관계를 예측합니다. 포인트 클라우드 분류 및 분할에서는 포인트 클라우드를 k-최근접 이웃 그래프 또는 오버레이 그래프로 변환하여 그래프 네트워크를 사용하여 관련 작업을 학습합니다. 최근에는 컴퓨터 비전 분야에서도 그래프 신경망의 적용 방향이 높아지고 있다. 일부 연구자들은 객체 감지와 같은 일반적인 컴퓨터 비전 작업에서 관련 탐색과 시도를 해왔습니다. 예를 들어, Huawei는 그래프 표현을 기반으로 하는 새로운 일반 시각적 아키텍처를 제안했습니다. ViG에서 연구원들은 입력 이미지를 여러 개의 작은 블록으로 나누고 해당 노드 그래프를 구성했습니다. 실험 결과는 행렬이나 그리드에 비해 그래프 구조가 객체 구성 요소를 더 많이 나타낼 수 있음을 보여줍니다. 보다 이상적인 결과를 얻기 위해 그들 사이의 관계를 유연하게 조정합니다.
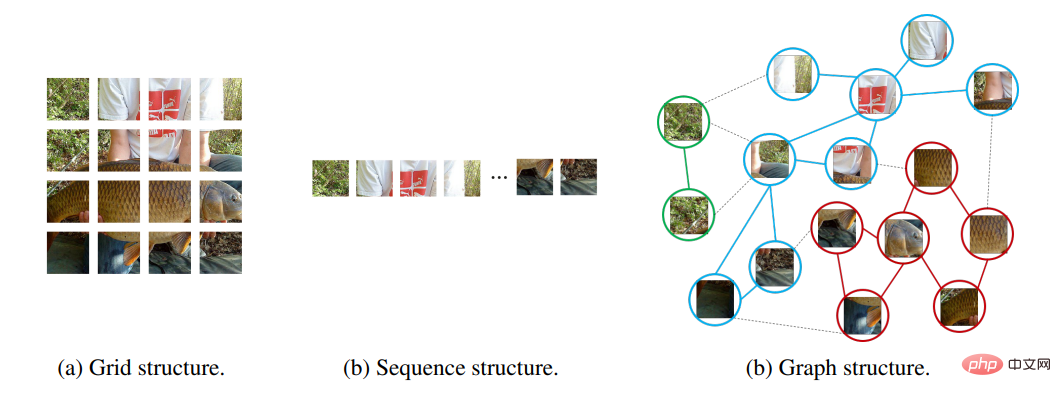
출처: Vision GNN@NeurIPS 2022
스마트 교통: 교통의 스마트 관리는 현대 도시에서 뜨거운 이슈입니다. 교통 네트워크의 교통 속도, 교통량 또는 도로 밀도를 정확하게 예측하는 것은 경로 계획 및 흐름 제어에 중요합니다. 교통 흐름의 매우 비선형적이고 복잡한 특성으로 인해 기존 기계 학습 방법으로는 공간적 및 시간적 종속성을 동시에 학습하는 것이 어렵습니다. 온라인 여행 플랫폼과 물류 서비스의 급속한 발전은 지능형 운송을 위한 풍부한 데이터 시나리오를 제공했습니다. 더 나은 교통 흐름 분석 및 관리를 달성하기 위해 신경망을 사용하여 교통 데이터의 시공간 상관 관계를 자동으로 학습하는 방법이 연구 핫스팟이 되었습니다. 도시 교통(아래 그림 참조)은 자연적으로 불규칙한 그리드 형태로 존재하기 때문에 지능형 교통 관리를 위해 그래프 신경망을 사용하는 것은 매우 자연스러운 탐구입니다.
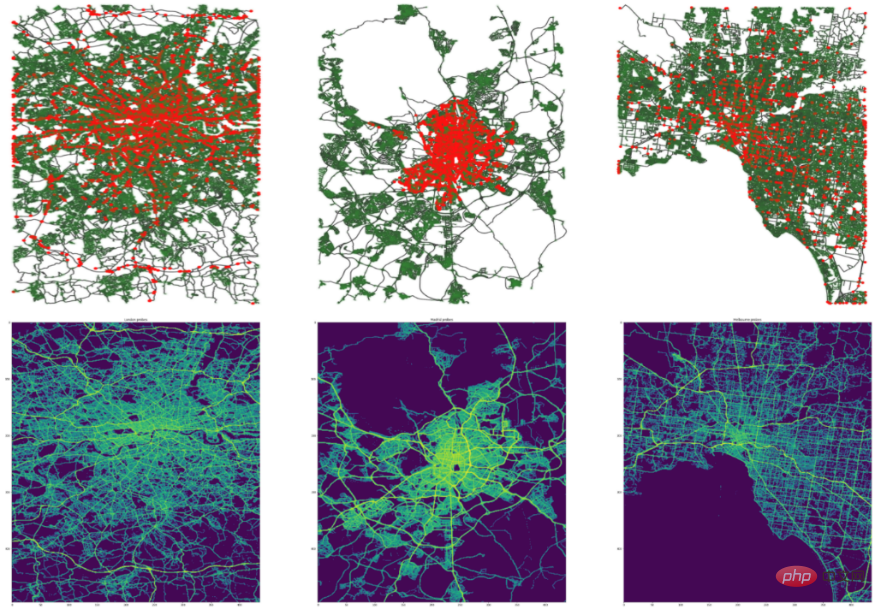
출처: Traffic4Cast@NeurIPS 2022
예를 들어, 고전적인 시공간 네트워크 STGCN은 GCN을 사용하여 각 순간의 교통 흐름 지도에 대한 공간적 특징을 포착합니다. 이 두 작업은 시간 차원에서 컨볼루션을 통해 시간적 특징을 포착합니다. 시공간적 차원 모두에서 기능에 대한 엔드투엔드 학습을 달성합니다. 다중 소스 정보를 사용하여 다양한 관점에서 노드 연관 그래프를 구성하고 정보를 집계하여 보다 정확한 예측 효과를 얻는 해당 작업도 있습니다. 그래프 신경망은 교통 예측 외에도 신호등 관리, 교통 이벤트 감지, 차량 궤적 예측, 도로 혼잡 예측 등 다양한 측면에서 사용됩니다. 최근 몇 년 동안 KDD 및 NeurIPS와 같은 주요 컨퍼런스의 관련 대회에서도 해당 교통 예측 질문이 설정되었으며 우승자 솔루션에는 기본적으로 그래프 신경망이 포함됩니다. 시공간 역학이 동시에 존재하기 때문에 지능형 교통 분야의 관련 응용 요구가 시공간 그래프 신경망 개발의 가장 중요한 동인이라고 해도 과언이 아닙니다.
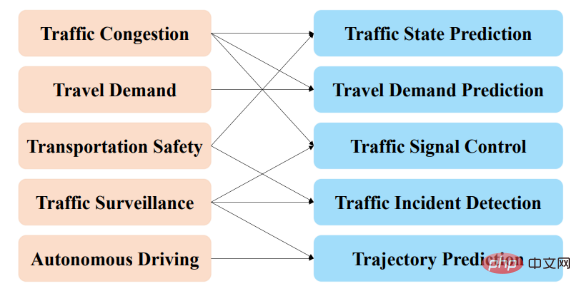
재무 위험 관리: 시장 경제의 발전과 산업의 디지털화 과정에 따라 다수의 전통 기업이 온라인으로 이전하는 가운데, 다양한 새로운 온라인 제품과 서비스도 날로 증가하고 있습니다. 엄청난 양의 데이터와 복잡한 관계로 인해 금융 거래 및 관련 감사에 큰 어려움이 따릅니다. 상장기업의 은행신용관리와 리스크관리는 금융시장의 질서를 유지하는데 중요한 역할을 합니다. Alipay, Paypal 등 신흥 글로벌 결제 관리 시스템이 홍보되면서 이를 보호하는 결제 위험 통제 시스템은 사용자 자금의 보안을 보호하고 카드 도난 및 계정 도난을 방지하며 플랫폼 손실을 줄이는 데 중요한 역할을 합니다. 그러나 기존 알고리즘으로는 관련 정보가 포함된 그래프 네트워크 데이터 분석을 해결하는 데 충분하지 않습니다. 그래프 신경망의 그래프 데이터 처리 기능 덕분에 다양한 금융 위험 제어 시나리오에서 일련의 사례가 등장했습니다. 예를 들어, 거래 과정에서 대출 전후 위험 평가, 가상계좌/사기/사기 탐지 등이 있습니다. 그래프 딥러닝 기술의 적용은 위험 통제 분야에서 효과적이고 필요한 것으로 입증되었지만, 산업 데이터의 프라이버시로 인해 개발 시간이 짧고 전반적인 프로세스가 아직 초기 단계에 있습니다. 기술 혁신은 여전히 해당 기업을 기반으로 하고 있으며 그 중 Ant Financial과 Amazon이 가장 두드러집니다. 예를 들어 Ant Financial에서 제안한 GeniePath 알고리즘은 계정에 대한 2클래스 분류 문제로 정의됩니다. 그래프 컨볼루션을 사용하여 악성 계정을 식별하는 Ant Financial에서 제안한 GEM 알고리즘은 주로 계정 로그인/등록에 사용됩니다. 시나리오. 데이터의 프라이버시와 시나리오의 다양성으로 인해 업계에서는 모델 비교 및 검증을 위한 통일된 표준이 부족합니다. 최근 Xinye Technology와 Zhejiang University는 사기 및 기타 이상 탐지 시나리오 검증을 위한 실제 시나리오의 대규모 데이터를 제공하는 대규모 동적 그래프 데이터 세트 DGraph를 공동으로 출시했습니다. 노드는 Xinye가 서비스를 제공하는 금융 대출 사용자를 나타냅니다. Edge는 긴급 연락 관계를 나타내며, 각 노드에는 민감하지 않은 속성 특성과 사용자가 금융 사기 사용자인지 여부를 나타내는 레이블이 포함되어 있습니다. 데이터 장벽, 금융 위험 제어 시나리오에서 만연한 데이터 불균형, 라벨 획득의 어려움, 모델 해석성에 대한 요구와 같은 문제가 있지만 그래프 신경망 개발에 새로운 사고와 기회도 가져왔습니다.
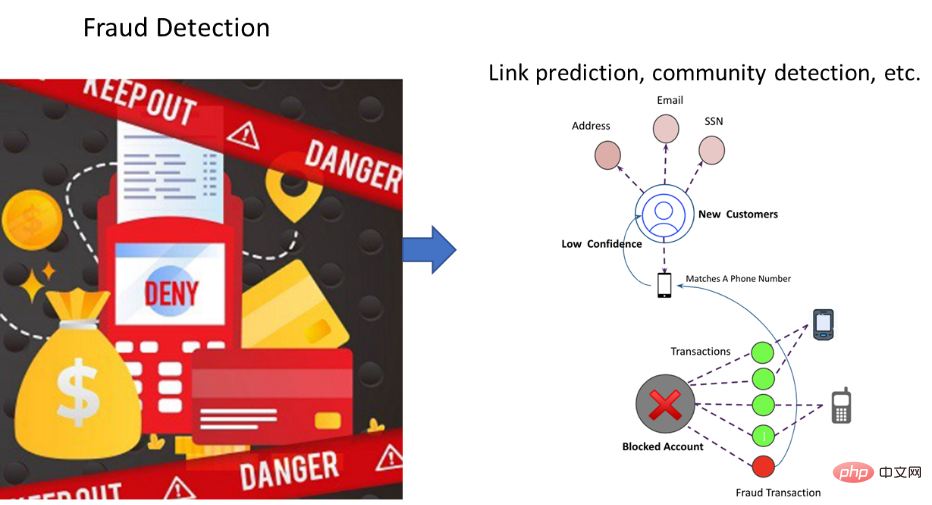
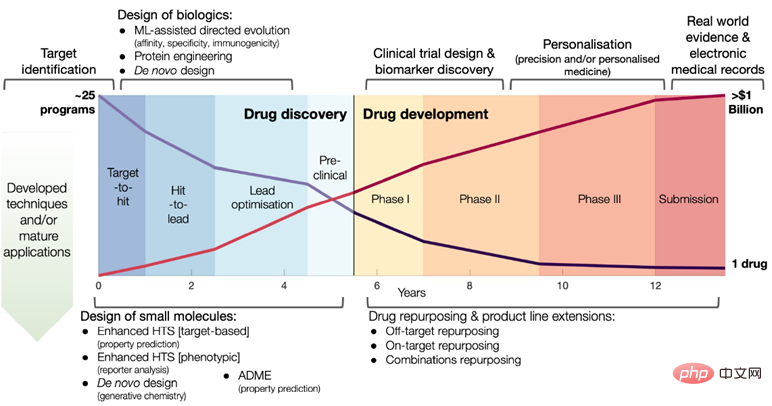
약물 발견: 약물 개발은 초기 약품 설계 및 분자 스크리닝부터 이후 안전성 테스트, 임상 시험 및 신약 연구에 이르기까지 긴 주기, 높은 비용 및 위험이 있는 대규모 프로젝트입니다. 개발 주기는 약 10~15년이 소요되며, 각 의약품의 평균 연구개발 비용은 약 30억 달러에 달합니다. 이 과정에서 약 1/3의 시간과 비용이 신약 발굴 단계에 소요됩니다. 특히 코로나19 등 전염병이 창궐하는 상황에서 어떻게 딥러닝 모델을 효과적으로 활용해 가능성 있고 다양한 후보 분자를 신속하게 발굴하고 신약 개발 과정을 가속화할 수 있을지는 많은 연구자들의 고민과 참여를 불러일으켰다.
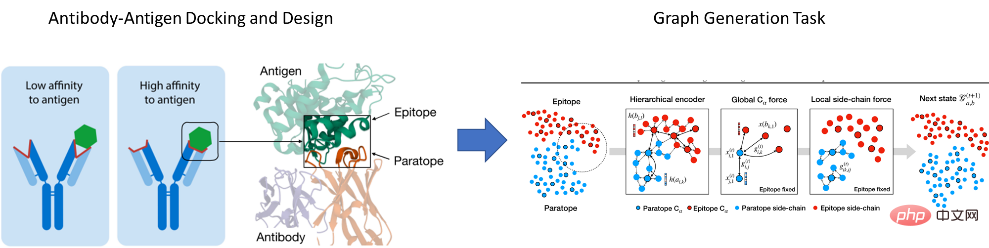
약물 연구 및 개발에 관련된 분자 화합물, 단백질 및 기타 물질은 그래프 구조에 자연스럽게 존재합니다. 분자를 예로 들면, 그래프의 가장자리는 분자 내 원자 간의 결합일 수도 있고 단백질 내 아미노산 잔기 간의 상호 작용일 수도 있습니다. 그리고 더 큰 규모에서 그래프는 단백질, mRNA 또는 대사산물과 같은 더 복잡한 구조 간의 상호 작용을 나타낼 수 있습니다. 세포 네트워크에서 노드는 세포, 종양 및 림프구를 나타낼 수 있으며 가장자리는 이들 사이의 공간적 근접성을 나타냅니다. 따라서 그래프 신경망은 분자 특성 예측, 고처리량 스크리닝, 신약 설계, 단백질 공학 및 약물 재사용 분야에서 광범위한 응용 가능성을 가지고 있습니다. 예를 들어, MIT CSIAL 연구원과 공동 연구자는 그래프 신경망을 사용하여 분자에 항생 특성이 있는지 예측하는 Cell(2020) 연구 결과를 발표했습니다. 올해도 같은 그룹 구성원들은 특정 항원과 일치도가 높은 항체를 설계하기 위해 그래프 생성 방식을 기반으로 항원 기반 조건부 생성 모델을 구축하는 등 일련의 작업을 제안했다. Mila Labs는 약물 발견에 그래프 학습을 적용하는 선구자이기도 하며, 최근 해당 탐색을 기반으로 하는 PyTorch 기반 약물 발견 기계 학습 플랫폼 TorchDrug를 오픈소스화했습니다. 또한, 주요 기술 기업들도 최근 몇 년 동안 AI 제약 분야에서 계획과 탐구를 진행해 이에 상응하는 뛰어난 성과를 거두었습니다. Tencent AI Lab의 'Yunshen' 플랫폼은 업계 최초의 대규모 의약품 AI용 비유통 연구 프레임워크인 DrugOOD를 출시했습니다. , 의약품 연구 개발 산업의 발전을 돕기 위해 제약 화학 시나리오의 유통 변화 문제에 대한 연구를 촉진합니다. Baidu 창립자 Robin Li가 설립한 Baidu Biotechnology는 첨단 AI 기술과 최첨단 생명공학을 결합하여 고유한 표적 발견 및 약물 설계를 만드는 데 전념하고 있습니다.
칩 디자인: 칩은 디지털 시대의 영혼이자 정보 산업의 3대 요소 중 하나입니다. 그래프 구조 데이터는 칩 설계의 여러 단계를 거쳐 실행됩니다. 예를 들어 논리 합성 단계에서는 디지털 회로가 NAND 그래프로 표현됩니다. 엔지니어는 논리 제약 조건에 의해 생성된 회로 넷리스트를 기반으로 상관 관계를 생성합니다. 특정 밀도 및 혼잡 제한 요구 사항에 따라 칩의 레이아웃 및 라우팅을 완료합니다.
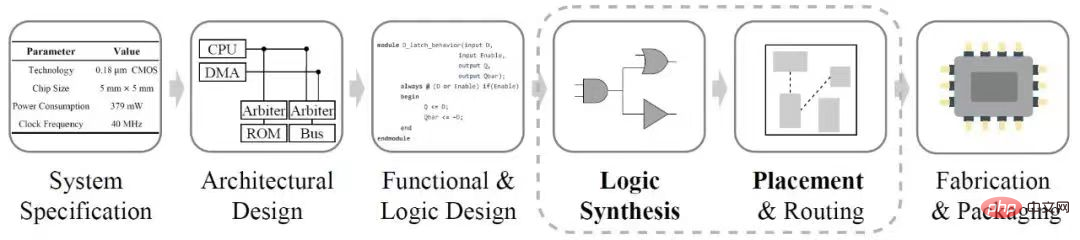
회로 크기와 복잡성이 지속적으로 증가함에 따라 EDA(전자 설계 자동화) 도구의 설계 효율성과 정확성이 중요한 문제가 되었으며, 이로 인해 연구의 관심이 높아지고 있습니다. 연구자들은 딥 러닝을 사용합니다 회로 설계 프로세스를 지원하는 기술입니다. 칩 설계 초기 단계에서 회로 품질과 유용성을 예측할 수 있다면 칩 반복 효율성이 향상되고 설계 비용이 절감될 수 있습니다. 예를 들어, 물리적 설계 단계에서 회로의 혼잡을 예측하면 결함을 감지하고 결함 칩 생성을 방지하는 데 도움이 될 수 있습니다. 이러한 예측이 논리 합성 단계에서 이루어질 수 있다면 칩의 설계 및 생산 주기가 더욱 단축될 수 있습니다. Google과 Stanford University 팀은 Google TPU 칩 블록의 전력 소비, 면적 및 성능 최적화와 같은 강화 학습과 결합하여 하드웨어 설계에 GNN을 성공적으로 사용했습니다. 칩 넷리스트 표현의 다양한 이종 정보를 고려하여 Huawei와 Peking University가 제안한 Circuit GNN은 토폴로지 및 기하학적 정보를 통합하여 맵을 구성하여 셀 및 네트 속성 예측을 위한 다양한 EDA 작업의 성능을 향상시킬 수 있습니다.
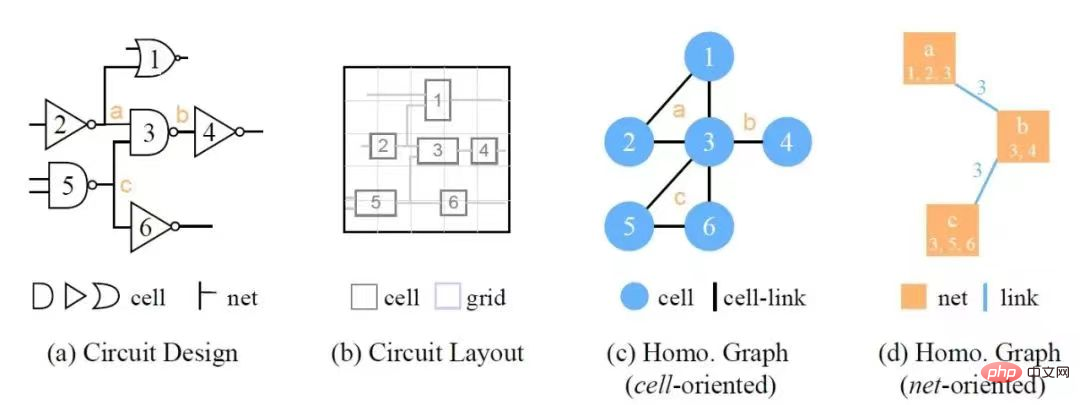
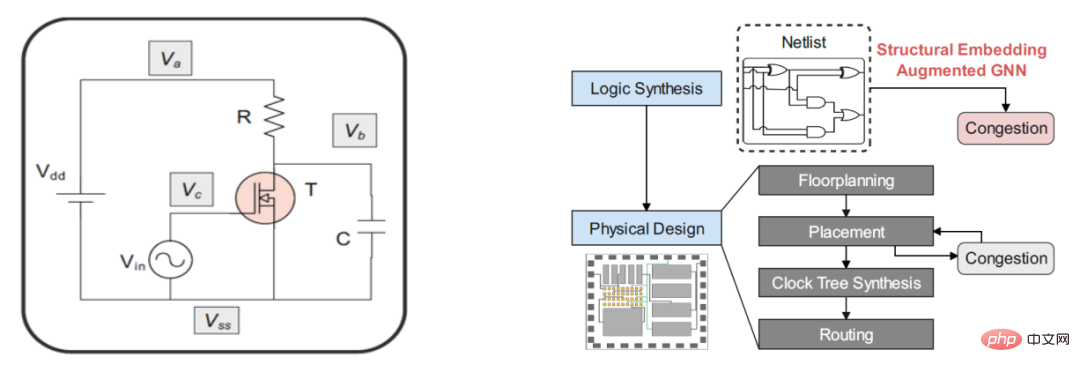
그래프 신경망은 여러 분야 외에도 프로그램 검증, 사회적 영향 예측, 뇌 네트워크, 이벤트 감지, 모델 시뮬레이션, 및 조합 최적화 문제 해결. 과학과 생명의 여러 분야에서 데이터를 그래프 구조로 표현할 수 있음을 알 수 있다. 그래프 신경망은 구조 정보와 그래프 속성 정보를 효과적으로 캡처함으로써 다양한 그래프 작업에서 높은 정확도를 달성했으며 향후 그래프 관련 문제를 해결하는 효과적인 수단이 될 것이라고 믿습니다. 그래프 신경망의 모습입니다.
4. 그래프 신경망의 확장성
이전 콘텐츠에서는 그래프 모델의 몇 가지 기본 패러다임과 해당 응용 시나리오를 소개했는데, 새로운 딥 러닝 아키텍처인 그래프 신경망이 소셜 네트워크에 매우 유용하다는 것을 알 수 있습니다. , 추천 시스템, 생물 의학 발견 및 기타 다양한 분야가 밝게 빛나고 있습니다. 그러나 실제 응용 프로그램에서 그래픽 모델의 확장성과 유용성은 여전히 많은 이론적, 공학적 과제에 직면해 있습니다. 첫 번째는 메모리 제한입니다. 설계 초기에는 GCN의 컨볼루션 작업이 전체 그래프에 대해 수행되었습니다. 즉, 각 레이어의 컨볼루션 작업이 전체 그래프를 통과하게 되므로 실제 애플리케이션에서는 필요한 메모리와 시간 오버헤드가 허용되지 않습니다. 또한 기존 머신러닝 프레임워크에서는 모델의 손실 함수를 개별 샘플의 손실 합계로 분해할 수 있으므로 미니 배치 및 확률론적 최적화를 사용하여 GPU 메모리보다 훨씬 큰 훈련 세트를 처리할 수 있습니다. 그러나 GNN 훈련에서는 샘플이 독립적인 머신러닝의 표준 데이터 세트와 달리 네트워크 데이터의 관계 구조가 샘플 간에 통계적 종속성을 생성합니다. 무작위 샘플링을 통해 직접 Mini-Batch 학습을 수행하면 모델 효과가 크게 감소하는 경우가 많습니다. 그러나 하위 그래프가 전체 그래프의 의미를 유지하고 GNN 교육을 위한 신뢰할 수 있는 기울기를 제공하는지 확인하는 것은 간단한 문제가 아닙니다. 두 번째는 하드웨어 제한입니다. 이미지 데이터 및 텍스트 데이터에 비해 그래프는 본질적으로 희소한 구조이므로 효율적이고 확장 가능한 계산을 위해 희소성을 활용해야 합니다. 그러나 해당 딥러닝 프로세서 및 관련 하드웨어의 현재 설계는 행렬 집약적인 작업을 처리하는 것을 목표로 합니다. 이번 절에서는 주로 그래프 모델의 확장성에 대해 요약합니다. 케임브리지 대학교 박사과정 학생인 Chaitanya K. Joshi의 요약을 보면 관련 작업은 데이터 전처리, 효율적인 모델 아키텍처, 새로운 학습 패러다임, 하드웨어 가속의 네 가지 측면으로 요약될 수 있습니다(아래 그림 참조). .
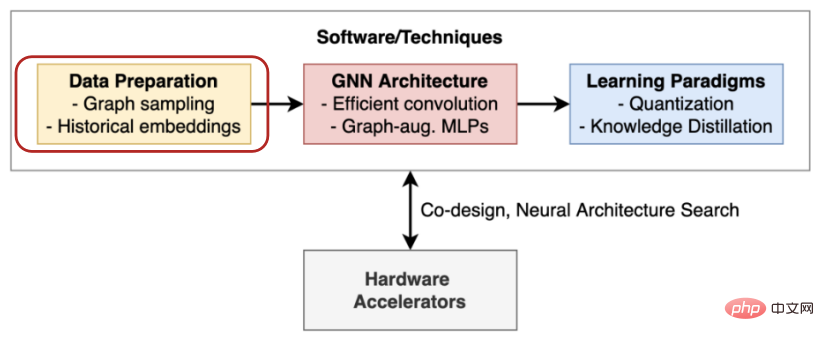
데이터 전처리는 일반적으로 원본 데이터를 샘플링하거나 단순화하여 대규모 그래프 데이터 계산을 구현합니다(아래에서 자세히 설명합니다). 새로운 아키텍처는 특정 작업이나 데이터의 관점에서 새롭고 더 효율적이며 간결한 아키텍처를 제안합니다. 예를 들어 LightGCN은 실행 속도를 높이기 위해 인접한 노드 사이의 내부 제품 부분을 제거합니다. 일부 연구에서는 노드 기능에서 MLP를 실행한 후 레이블 전파 방법을 사용하는 것도 좋은 결과를 얻을 수 있음을 발견했습니다. 또한 지식 증류 또는 양자화 인식 훈련과 같은 일부 경량 학습 패러다임을 통해 GNN의 성능을 향상하고 대기 시간을 줄일 수도 있습니다. 언급할 점은 위에서 언급한 그래프 신경망 훈련 가속화 방법이 서로 분리되어 있다는 점입니다. 이는 실제 시나리오에서 여러 방법을 동시에 사용할 수 있음을 의미합니다.
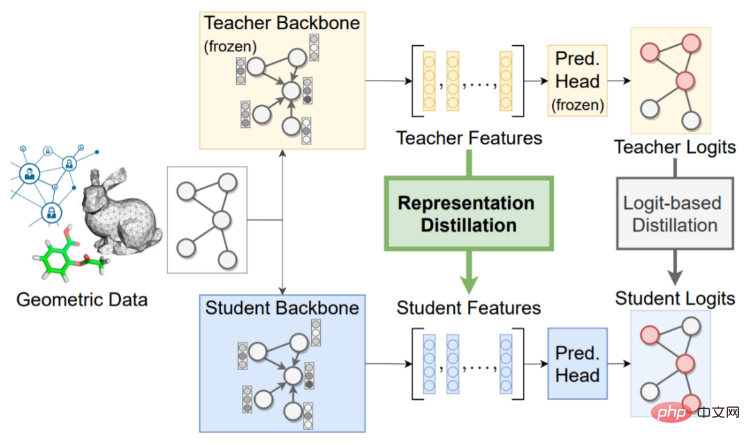
출처: G-CRD@TNNLS
모델 최적화 및 새로운 학습 패러다임에 비해 데이터 전처리는 더 일반적이고 적용 가능한 방법이며 현재도 상대적으로 말하고 있습니다. 여기서는 분석과 소개를 약간 확장하겠습니다. 일반적으로 데이터 전처리 방법은 일부 샘플링 또는 그래프 단순화를 사용하여 메모리 제약 조건을 충족할 수 있도록 원본 이미지의 크기를 줄입니다.
1. 샘플링 기반 데이터 처리
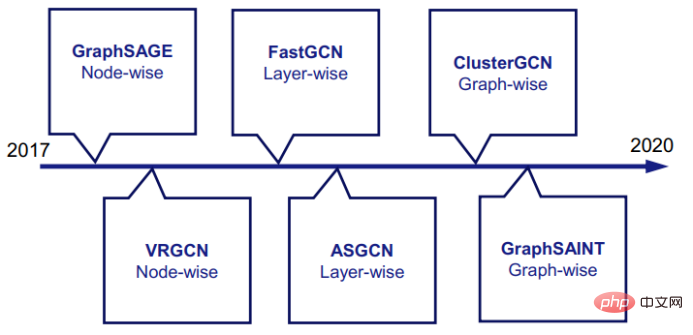
샘플링 기반 방법은 Node-Wise Sampling, Layer-Wise Sampling 및 Graph-Wise Sampling의 세 가지 하위 범주로 나눌 수 있습니다.
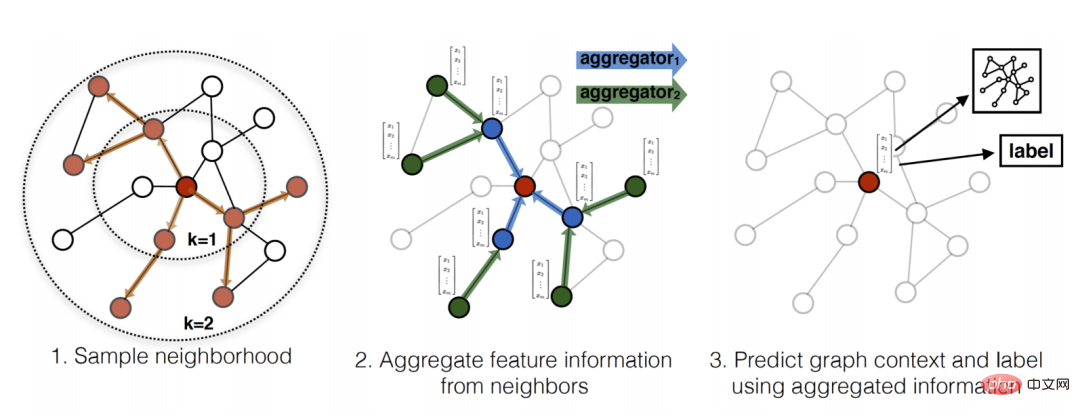
Node-Wise Sampling: GraphSage에서 처음 제안한 방법으로 비교적 일반적이고 효과적이며 가장 널리 사용됩니다. GraphSAGE의 한 레이어는 1-홉 이웃의 정보를 집계합니다. GraphSAGE의 k 레이어를 오버레이하면 k-홉 이웃에 의해 유도된 하위 그래프로 수용 필드가 증가할 수 있으며, 이는 이웃의 속도를 제어할 수 있습니다. 집계 작업을 수행하고 이웃 수를 줄이면 계산량이 줄어듭니다. 그러나 레이어 수가 증가함에 따라 샘플링된 이웃의 수도 기하급수적으로 증가한다는 점에 유의해야 합니다. 이는 결국 k-hop 이웃에 의해 유도된 하위 그래프에 대한 메시지 집계와 동일하며 시간 복잡도는 다음과 같습니다. 실질적이지 않습니다.
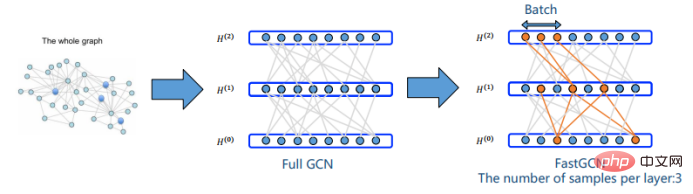
Lay-Wise 샘플링: 은 Fast GCN과 달리 중요도 샘플링 방식인 모든 노드에서 샘플링을 통해 노드의 이웃 샘플링 범위를 직접 제한합니다. 작은 배치에서 GraphSAGE의 각 샘플 노드의 이웃 세트는 독립적인 반면 Fast GCN의 모든 샘플 노드는 동일한 이웃 세트를 공유하므로 계산 복잡성을 선형 수준으로 직접 제어할 수 있습니다. 우리가 처리하고 있는 그래프가 크고 희박하기 때문에 이 방법으로 샘플링된 인접 레이어의 샘플은 전혀 관련이 없어 학습에 실패할 수 있습니다.
Graph-wise Sampling: Neighbor Sampling 방식과 달리 그래프 샘플링 기법은 원본 이미지에서 하위 그래프를 샘플링하는 것입니다. 예를 들어 Cluster GCN은 클러스터링이라는 아이디어를 사용하여 나눕니다. 그래프를 작은 블록으로 나누어 그래프 샘플링을 구현합니다. 그래프 클러스터링 알고리즘(예: METIS)은 유사한 노드를 그룹화하여 클래스 내의 노드 분포가 원래 그래프의 노드 분포에서 벗어나게 합니다. 그래프 샘플링으로 인해 발생하는 문제를 해결하기 위해 Cluster GCN은 여러 범주를 동시에 배치로 추출하여 노드 분포의 균형을 맞추기 위한 훈련에 참여합니다. 그러나 구조 기반 샘플링 방법은 정보 손실이 상대적으로 크고, 대부분의 데이터 결과가 풀배치 GNN에 비해 크기 때문에 각 에포크마다 샘플링해야 하며 시간 오버헤드도 작지 않습니다.
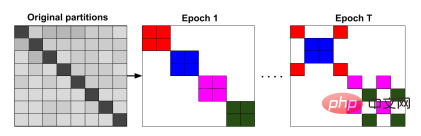
2. 그래프 단순화 기반
샘플링 외에도 일부 그래프 축소 방법(그래프 축소)을 사용하여 후속 이미지의 주요 속성을 유지하면서 원본 이미지의 크기를 줄일 수 있습니다. 처리 및 분석이 가능한 방향. 그래프 단순화에는 주로 그래프 희소화(그래프의 간선 수 감소)와 그래프 조잡화(그래프의 정점 수 감소)가 포함됩니다.

그중 그래프 조대화는 원래 그래프 규모의 단순화를 달성하기 위해 "핀치 포인트"를 통해 일부 하위 그래프를 슈퍼 노드로 집계하는 데 적합한 프레임워크입니다. GNN 가속 훈련을 위해 그래프 조대화를 사용하는 알고리즘은 KDD 2021 작업에서 처음 제안되었습니다. 프로세스는 아래 그림과 같습니다.
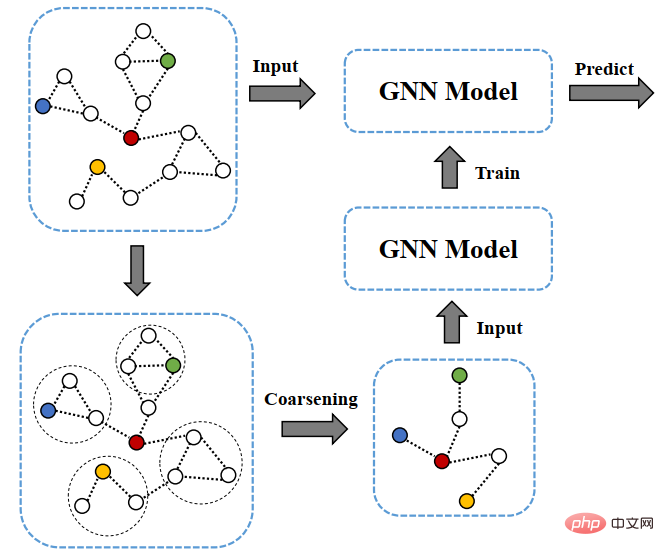
먼저 그래프 조대화 알고리즘(예: 스펙트럼 클러스터링 조대화)을 사용합니다. 원본 이미지를 거칠게 하고, 거칠어진 그래프 G'를 기반으로 모델을 훈련함으로써 그래프 신경망 훈련에 필요한 매개변수를 줄일 수 있을 뿐만 아니라 훈련 시간과 실행 메모리 오버헤드를 줄입니다. 이 방법은 보편적으로 간단하며 선형 훈련 시간과 공간을 갖습니다. 저자의 이론적 분석은 또한 스펙트럼 클러스터링에 의해 거칠어진 그래프에 대한 APPNP 훈련이 원래 그래프에 대한 제한된 APPNP 훈련과 동일하다는 것을 보여줍니다. 그러나 그래프 샘플링 방법과 마찬가지로 그래프 조대화 기반 방법에도 데이터 전처리가 필요하며 시간 오버헤드는 실험 결과 및 조대화 알고리즘 선택과 관련이 있습니다.
마찬가지로 위에서 소개한 샘플링이나 단순화를 기반으로 한 여러 그래프 모델 확장 방법도 서로 분리되어 있어 Cluster GCN + GraphSAGE와 같이 여러 방법을 동시에 함께 사용할 수 있습니다. 본질적으로 k-hop 이웃에 의해 유도된 하위 그래프에 메시지를 집계하는 것은 지수 연산입니다. 원본 이미지를 다운샘플링하는 동안 정보 손실 없이 선형 수준에서 노드 샘플링을 기반으로 하는 알고리즘의 시간 복잡도를 제어하는 것은 어렵습니다. 계산을 위해 전체 이미지를 메모리에 넣을 수 있다면 GCN의 시간 복잡도는 선형이 되지만 전처리 비용은 무시할 수 없기 때문에 좋은 솔루션입니다. 세상에 공짜 점심은 없습니다. 그래프 신경망의 훈련 가속화에는 여전히 정보 손실과 전처리 오버헤드 간의 균형이 필요합니다.
또한 그래프는 본질적으로 희소 객체이므로 디자인 효율성과 확장성에 관해서는 데이터 희소성 관점에서 더 생각해야 합니다. 그러나 최신 GPU는 행렬에 대한 집중적인 작업을 처리하도록 설계되었기 때문에 이는 말처럼 쉽지 않습니다. 희소 행렬을 위한 맞춤형 하드웨어 가속기는 GNN의 적시성과 확장성을 크게 향상시킬 수 있지만 관련 작업은 아직 개발 초기 단계에 있습니다. 또한, 그래프 컴퓨팅을 위한 커뮤니케이션 전략의 설계 역시 최근 많은 관심을 받고 있는 방향이다. 예를 들어, VLDB2022 및 Webconf 2022의 최우수 연구 논문 및 최우수 학생 논문상은 그래프 모델 처리를 가속화하는 시스템 또는 알고리즘에 수여되었습니다. 그중 SANCUS@VLDB2022는 통신량을 줄이고 분산 메커니즘을 사용하여 그래프 신경망의 분산 학습을 가속화하는 것을 목표로 분산 학습 프레임워크(SANCUS) 세트를 제안했습니다. 이 기사에서는 SANCUS의 수렴 속도가 전체 그래프 훈련에 가깝다는 것을 이론적으로 증명했을 뿐만 아니라, 수많은 실제 장면 그래프에 대한 실험을 통해 SANCUS의 훈련 효율성과 정확성을 검증했습니다. PASCA@Webconf2022의 작업은 메시지 전달 프레임워크에서 메시지 집계 작업과 업데이트 작업을 분리하려고 시도하고 분산 시나리오에서 통신 오버헤드를 달성하기 위한 전처리-훈련-후처리의 새로운 패러다임을 정의합니다.
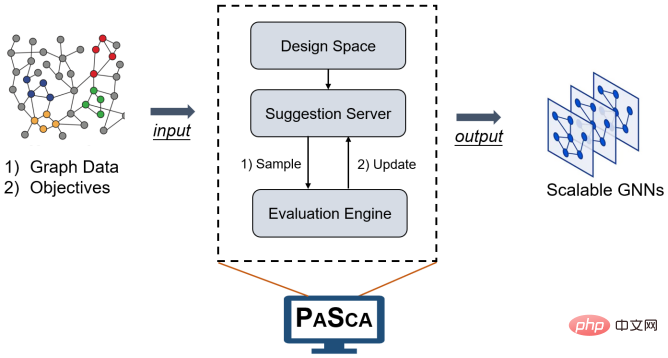
출처: PASCA@Webconf2022
5 그래프 신경망 설계 및 학습 공간
덕분에 컴퓨팅 리소스의 급속한 성장 네트워크 표현 능력을 갖춘 딥러닝은 지식 마이닝을 위한 중요한 도구가 되었습니다. 그래프는 개체와 그 관계를 간결한 형태로 표현하고 자연 과학 및 사회 과학 응용 분야 어디에서나 사용되는 다양하고 강력한 데이터 구조입니다. 그러나 실제 세계의 그래프 데이터는 구조, 내용, 작업이 매우 다양합니다. 한 작업에 대해 가장 우수한 성능을 보이는 GNN 네트워크 및 아키텍처 설계는 다른 작업에는 적합하지 않을 수 있습니다. 주어진 데이터 세트와 예측 작업에 대해 좋은 결과를 갖는 모델을 빠르게 얻는 방법은 연구자나 응용 알고리즘 엔지니어에게 매우 의미가 있습니다. 주어진 데이터 세트와 예측 작업에 어떤 신경망 아키텍처가 효과적인가요? 좋은 GNN 디자인을 자동으로 예측하는 시스템을 구축할 수 있습니까? 이러한 생각을 바탕으로 Jure Leskovec 그룹은 2020년 그래프 신경망 설계 공간에 대한 출판 작업에서 GNN의 설계 공간을 세 가지 수준으로 정의했습니다. 이 작업은 또한 그래프 자동 기계 및 그래프 모델의 후속 마이그레이션을 위한 기초를 제공합니다. 기초.
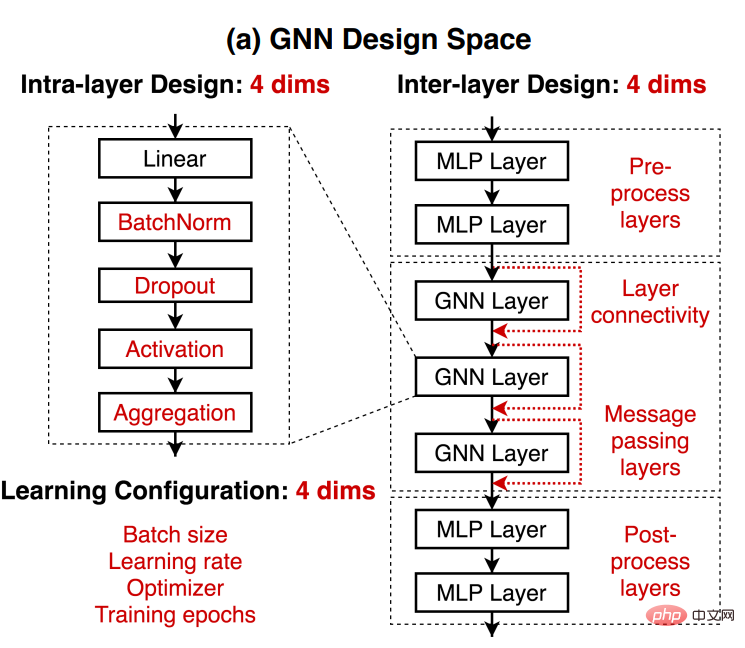
특정 작업과 특정 데이터 세트가 주어지면 먼저 다음을 전달할 수 있습니다.
(1) 레이어 내 디자인: 단일 GNN 레이어의 디자인.
(2) Inter-layer 디자인: GNN 레이어를 연결하는 방법.
(3) 학습 구성: 기계 학습을 위한 매개 변수를 설정하는 방법입니다.
세 가지 방향으로 해당 GNN 디자인 공간을 구성한 다음 모델의 순위를 지정하여 특정 작업에 대한 성능 차이를 정량화함으로써 주어진 데이터에서 최적의 모델 디자인을 이해할 수 있습니다. 또한 새로운 작업과 데이터의 경우 작업 공간에 있는 기존 컬렉션과 새 데이터 세트 간의 유사성을 간단히 계산하여 가장 유사한 작업을 빠르게 식별하고 최적의 모델을 새 데이터로 마이그레이션할 수도 있습니다. 세트. 이러한 방식으로 이전에 한 번도 사용된 적이 없는 데이터 세트에 대해 더 나은 모델을 더 빨리 얻을 수 있습니다. 물론, 그래프에 대한 자동 기계 학습과 그래프 모델의 전달성은 학술 연구와 산업 응용에 있어서 매우 중요한 문제입니다. 지난 2년 동안 관련 탐구와 생각이 많이 있었습니다. 여기서는 다루지 않겠습니다. 그래프의 자동 기계 학습에 대한 더 많은 작업을 보려면 Tsinghua University 교사 Zhu Wenwu의 학술 그룹과 오픈 소스 자동 학습 툴킷 AutoGL 및 네 번째 패러다임 관련 작업에 대한 관련 검토를 참조하시기 바랍니다. 업계.
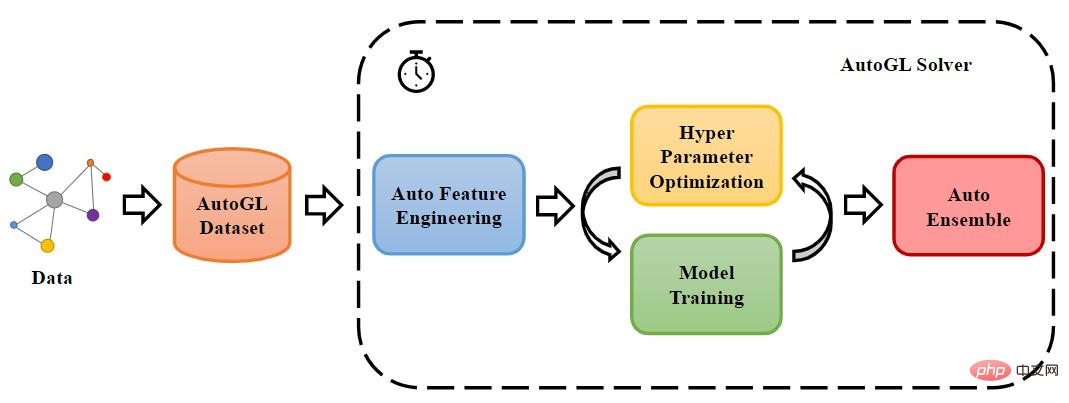
출처: AutoGL
위에서 언급한 모델 설계 공간은 주로 모델 구조 수준에 초점을 맞추고 있지만, 모델의 표현이나 학습 공간이라는 또 다른 매우 중요한 차원이 있는데, 보충제도 매우 유용합니다. 그래프 머신러닝은 그래프 데이터에 대한 표현 학습 방법으로, 원본 데이터를 학습하여 관찰 결과를 예측하는 것이 아니라 데이터의 기본 구조를 학습하여 원본 데이터의 해당 특징 학습이 가능하도록 하는 것이 목표입니다. 다운스트림 작업에서 더 나은 결과를 얻기 위해 더 잘 수행되고 표현됩니다.
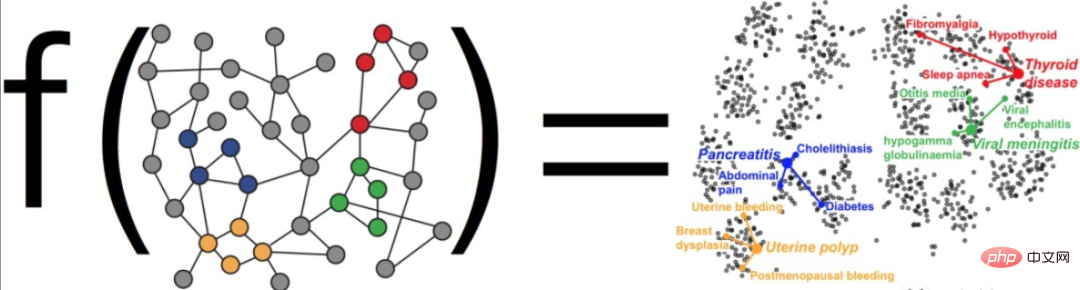
대부분의 표현 학습은 유클리드 공간에서 이루어집니다. 왜냐하면 유클리드 공간은 직관 친화적인 시각적 공간을 자연스럽게 일반화한 동시에 계산 친화적이고 컴퓨팅 이점도 있기 때문입니다. 그러나 우리 모두 알고 있듯이 그래프에는 비유클리드 구조가 있습니다. 예를 들어, 복잡한 네트워크 분야의 연구에 따르면 실제 네트워크 데이터(소셜 네트워크, 상품 네트워크, 통신 네트워크, 질병)에는 척도가 없는 속성이 많이 있는 것으로 나타났습니다. 네트워크, 의미 네트워크 등)(scale-free), 이는 트리형/계층적 구조가 실제로 어디에나 존재한다는 것을 의미합니다. 유클리드 공간을 표현학습의 사전 공간으로 활용하여 해당 모델링을 수행하게 되면 필연적으로 해당 오류(왜곡)가 발생하게 됩니다. 따라서 최근 다양한 곡률 공간을 기반으로 한 표현 학습이 모두의 관심을 끌고 있습니다. 곡률은 공간의 곡률을 측정한 값으로, 곡률이 0에 가까울수록 공간이 더 평평해집니다. SF 소설 '삼체 문제'에서 인간은 공간 곡률의 변화를 이용해 곡률 우주선을 만든다. 아래 그림과 같이 유클리드 공간은 어디에서나 균일하고 평평하며 등방성과 병진 불변성을 가지므로 그리드 데이터 모델링에 적합합니다. 양의 곡률을 갖는 구면 공간 거리 측정은 각도 측정과 동일하며 회전 불변성을 가지므로 링 데이터 또는 조밀하고 균일한 그래프 데이터 구조를 모델링하는 데 적합합니다. 음의 곡률을 갖는 쌍곡선 공간 거리 측정법은 거듭제곱 법칙 분포와 동일하며 척도 없는 네트워크 또는 트리 구조를 모델링하는 데 적합합니다.
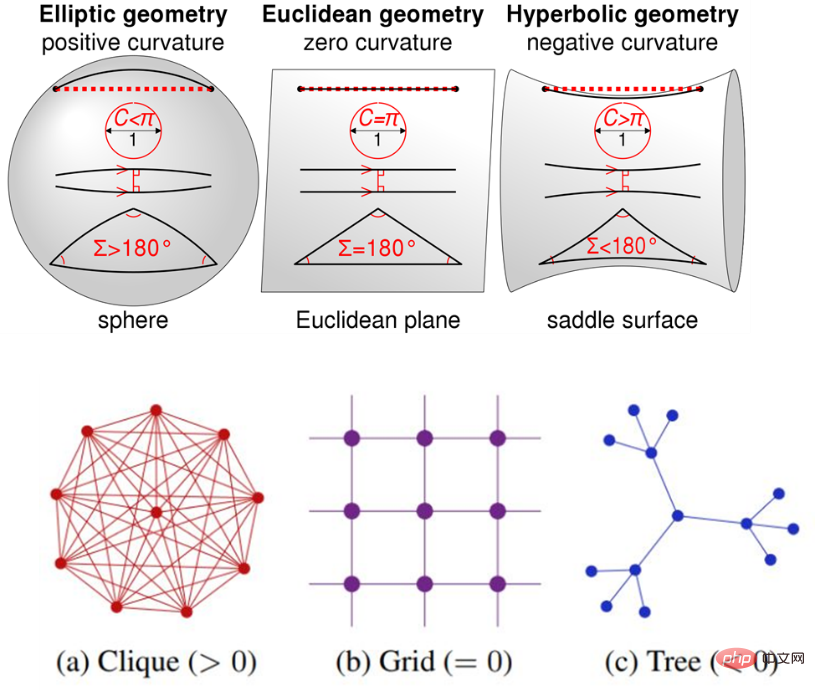
대량의 실제 네트워크 데이터에 존재하는 스케일 프리(scale-free) 특성으로 인해 현실에서는 트리형/계층적 구조가 어디에나 존재한다는 의미입니다. . 그 중 쌍곡선 공간은 전통적인 네트워크 과학 분야에서 트리/계층 구조의 연속적인 표현으로 간주되어 실제 데이터를 모델링하는 데 더 적합합니다. 또한, 유클리드 공간에 비해 쌍곡선 공간의 부피는 반지름에 따라 기하급수적으로 증가하므로 삽입 공간이 더 커집니다. 유클리드 공간과 달리 쌍곡선 공간에는 설명할 수 있는 여러 모델이 있습니다. 푸앵카레 볼을 예로 들어 간단히 소개하겠습니다.
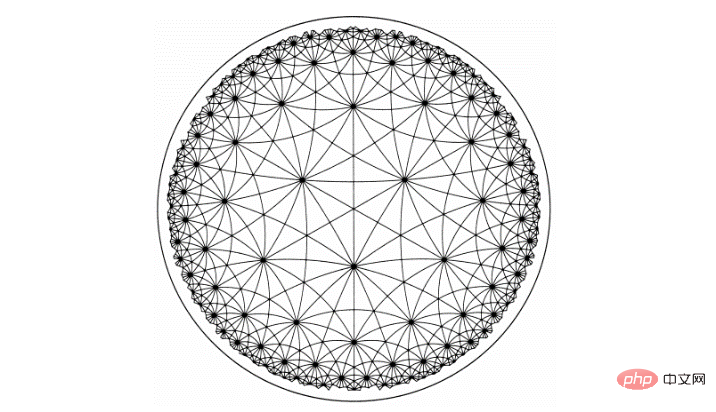
푸앵카레 디스크는 삽입 공간을 단위 구로 제한하는 쌍곡선 모델입니다. 푸앵카레 구의 쌍곡선 모델에서 위의 밝은 삼각형과 어두운 삼각형은 모두 동일한 크기이지만 유클리드 관점에서 보면 가장자리 근처의 삼각형은 상대적으로 작습니다. 다르게 말하면, 유럽의 관점에서 보면 위 원의 중심을 원점으로 하여 반지름이 커질수록 삼각형의 개수가 늘어나는 것을 상상해 볼 수 있습니다
쌍곡선 공간은 "풍선을 부는 것"과 같습니다. 수축된 풍선의 표면에 10억 개의 노드가 있다고 가정합니다. 이는 매우 밀도가 높은 상태입니다. 풍선이 점차 부풀어오르고 커짐에 따라 풍선의 표면은 점점 더 "곡선"이 되고 마디는 더욱 멀어집니다. Alimama의 기술팀은 Taobao 기반 검색 광고 시나리오에 곡률 공간(Curvlearn)을 적용했습니다. 시스템이 완전히 출시된 후 스토리지 소비가 80% 감소하고 사용자 측 요청 매칭 정확도가 15% 증가했습니다. 추천 시스템 외에도 쌍곡선 그래프 모델은 다양한 시나리오에서 우수한 결과를 보여주었습니다. 관련 콘텐츠에 관심이 있는 학생들은 올해 ECML-PKDD에서 쌍곡선 그래프 표현 학습 관련 튜토리얼을 참조할 수도 있습니다(홈페이지 포털: https://hyperbolicgraphlearning.github.io/ ) 또는 WebConf에서 Virginia Tech 및 Amazon과 같은 학자들이 작성한 쌍곡선 신경망 관련 튜토리얼.
6. 그래프 신경망 훈련 시스템, 프레임워크, 벤치마크 플랫폼
그래프 신경망 알고리즘은 심층 신경망의 작업(예: 컨볼루션, 그라디언트 계산)과 반복 그래프 전파를 결합합니다. 각 정점 특징이 계산됩니다. 일련의 심층 신경망과 결합된 이웃 정점의 특징을 활용합니다. 그러나 기존 딥러닝 프레임워크는 그래프 전파 모델을 확장하고 실행할 수 없으므로 그래프 신경망을 효율적으로 훈련하는 기능이 부족합니다. 또한 실제 세계의 그래프 데이터 규모는 엄청나며 정점 간에 복잡한 종속성이 있습니다. 예를 들어 Facebook의 소셜 네트워크 그래프에는 20억 개가 넘는 정점과 1조 개가 넘는 가장자리가 포함되어 있으며 이 크기의 그래프는 100TB를 생성할 수 있습니다. 기존 그래프 알고리즘과 달리 균형 그래프 분할은 파티션 내의 정점 수에 따라 달라질 뿐만 아니라 파티션 내 서로 다른 정점의 다중 순서 이웃 수에도 따라 달라집니다. -레이어 그래프 신경망 모델은 차이가 크고 이러한 파티션 간에 빈번한 데이터 교환이 필요합니다. 분산 훈련의 성능을 보장하기 위해 그래프 데이터를 합리적으로 분할하는 방법은 분산 시스템의 주요 과제입니다. 또한, 그래프 데이터가 매우 희박하여 분산 처리에서 노드 간 액세스가 빈번하게 발생하여 대량의 메시지 전달 오버헤드가 발생합니다. 따라서 그래프의 특수한 속성을 기반으로 시스템 오버헤드를 어떻게 줄이는 것이 시스템 성능 향상을 위한 주요 과제이다. 일꾼이 일을 잘하고 싶다면 먼저 도구를 갈고 닦아야 합니다. 대규모 그래프에 대한 그래프 신경망의 적용과 보다 복잡한 그래프 신경망 구조의 탐색을 지원하기 위해서는 그래프 신경망을 위한 훈련 시스템의 개발이 필요하다. 가장 먼저 언급할 것은 가장 잘 알려진 오픈소스 프레임워크인 PyG(PyTorch 기하학)와 DGL(Deep Graph Library)이다. 전자는 스탠포드 대학과 TU 도르트문트 대학이 공동 개발한 PyTorch 기반 그래프 신경망 라이브러리이고, 많은 GNN을 포함하고 있으며 관련 논문에서 일반적으로 사용되는 데이터 세트를 제공하고 있으며, 후자는 뉴욕대학교와 아마존 연구소가 공동으로 개발한 그래프 학습 프레임워크입니다. 학계와 산업계의 오픈 소스 프레임워크 모두 활발한 커뮤니티 지원을 받고 있습니다.

또한 많은 회사에서는 NeuGraph, EnGN, PSGraph, AliGraph, Roc, AGL, PGL, Galileo와 같이 자체 비즈니스 특성을 기반으로 자체 그래프 신경망 프레임워크 및 데이터베이스를 구축했습니다. , TuGraph, 각도 그래프 등 그 중 알리그래프(AliGraph)는 알리바바컴퓨팅플랫폼(Alibaba Computing Platform)과 DAMO 아카데미 지능형컴퓨팅연구소(DAMO Academy Intelligent Computing Laboratory)가 개발한 샘플링 모델링과 트레이닝을 통합한 그래프 신경망 플랫폼이다. PGL(Paddle Graph Learning)은 Baidu가 개발한 PaddlePaddle을 기반으로 하는 해당 그래프 학습 프레임워크입니다. Angle Graph는 Tencent TEG 데이터 플랫폼에서 출시한 대규모 고성능 그래프 컴퓨팅 플랫폼입니다.
벤치마크 플랫폼에 대해 다시 이야기해 보겠습니다. 딥 머신 러닝의 핵심 연구 또는 응용 분야에서 벤치마크 데이터 세트와 플랫폼은 어떤 유형의 아키텍처, 원리 또는 메커니즘이 보편적이고 실제 작업과 대규모 데이터 세트에 일반화될 수 있는지 식별하고 정량화하는 데 도움이 됩니다. 예를 들어, 신경망 모델의 최신 혁명은 대규모 벤치마크 이미지 데이터 세트인 ImageNet에 의해 촉발되었습니다. 그리드나 시퀀스 데이터에 비해 그래프 데이터 모델의 개발은 아직 상대적으로 자유로운 성장 단계에 있습니다. 첫째, 데이터 세트가 실제 시나리오와 일치하기에는 너무 작은 경우가 많습니다. 즉, 알고리즘을 안정적이고 엄격하게 평가하기가 어렵습니다. 둘째, 알고리즘 평가 방식이 일정하지 않습니다. 기본적으로 각 연구 논문은 자체적인 "훈련 세트/테스트 세트" 데이터 분할 방법과 성능 평가 지표를 사용합니다. 이는 논문과 아키텍처 전반에 걸쳐 성능 비교를 수행하기가 어렵다는 것을 의미합니다. 또한 다양한 연구자들이 데이터 세트를 분할할 때 전통적인 무작위 분할 방법을 사용하는 경우가 많습니다. 그래프 학습 커뮤니티의 일관되지 않은 데이터 및 작업 데이터 분할 방법과 평가 체계 문제를 해결하기 위해 스탠포드 대학교 Jure Leskovec 팀은 그래프 신경망 벤치마크 플랫폼의 기초 작업인 Open Graph Benchmark(OGB)를 2020년에 출시했습니다. .
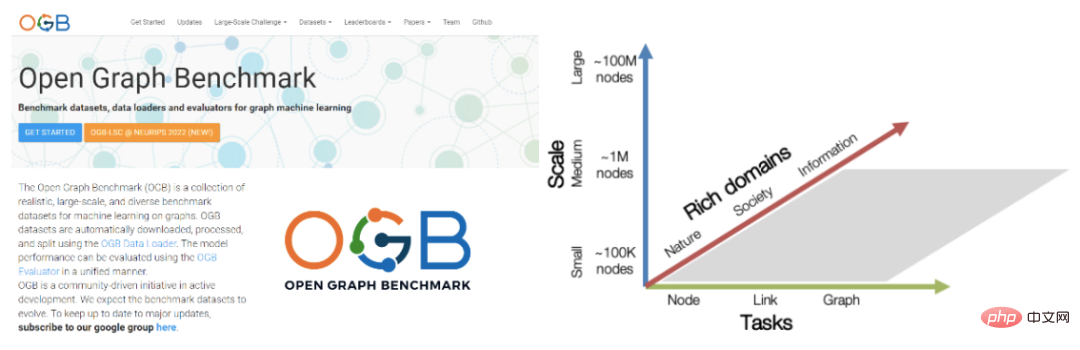
OGB에는 그래프의 주요 작업(노드 분류, 링크 예측, 그래프 분류 등)에 대해 바로 사용할 수 있는 데이터 세트와 공통 코드 라이브러리 및 성능 평가가 포함되어 있습니다. 지표의 구현 코드를 통해 빠른 모델 평가 및 비교가 가능합니다. 또한 OGB에는 모델 성과 순위 보드(리더보드)도 있어 모든 사람이 해당 연구 진행 상황을 빠르게 따라갈 수 있습니다. 또한 2021년 OGB는 KDD CUP과 공동으로 제1회 OGB-LSC(OGB Large-Scale Challenge) 대회를 개최하여 실제 세계의 초대형 그래프 데이터를 제공하여 노드 분류, 에지 예측 및 그래프 학습을 완료했습니다. 그래프 학습 분야는 세 가지 주요 과제로 돌아가서 Microsoft, Deepmind, Facebook, Alibaba, Baidu, ByteDance, Stanford, MIT, Peking University 등을 포함한 많은 최고의 대학 및 기술 기업의 참여를 이끌어냈습니다. 올해 NeurIPS2022 대회 트랙에서는 KDD 컵 경험을 바탕으로 해당 데이터 세트를 업데이트하고 제2회 OGB-LSC 대회를 편성했습니다
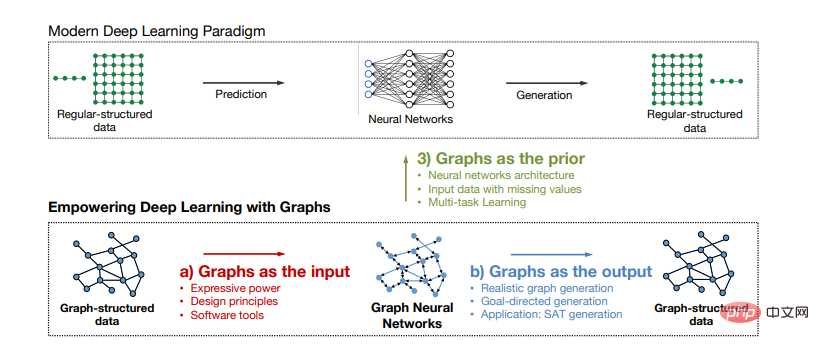
한 분야에 빨리 익숙해지는 좋은 방법 읽기 수준 연구실을 막 졸업한 학생의 박사 학위 논문입니다. SNAP 연구실의 Rex YING과 You Jiaxuan은 아래에서 그래프 학습과 관련된 연구를 시작했을 것입니다. 2016년과 2017년 각각 Jure Leskovec의 지도에 따라 많은 성과가 그래프 학습 개발의 랜드마크가 되었으며 각각의 박사 학위 논문 "Towards Expressive and Scalable Deep Representation Learning for Graphs" 및 "Empowering Deep Learning with Graphs"에 정리되었습니다. ")
. 7. 요약 및 전망
10년 이상의 개발과 최근 다양한 산업 분야의 산업적 응용, 실험실에서의 지속적인 이론 반복을 통해 그래프 신경망이 최선의 선택임이 입증되었습니다. 이론과 실습에서 그래프 구조의 데이터를 처리하는 효과적인 방법과 프레임워크입니다. 보편적이고 간결하며 강력한 데이터 구조인 그래프는 비유클리드 구조 데이터를 마이닝하고 학습하기 위한 그래프 모델의 입력 및 출력으로 사용될 수 있을 뿐만 아니라 유럽 데이터(텍스트 및 텍스트)를 모델링하기 위한 선험적 구조로 사용될 수도 있습니다. 사진). 장기적으로 우리는 그래프 데이터 + 신경망이 신흥 연구 분야에서 기계 학습 연구 및 응용을 위한 표준 데이터 + 모델 패러다임으로 전환되어 더 많은 산업과 시나리오에 힘을 실어줄 것이라고 믿습니다.
(전망을 피할 수 없음) GNN은 최근 몇 년 동안 응용 시나리오의 확장과 실제 동적 변화 및 알려지지 않은 개방 환경으로 인해 많은 분야에서 큰 성공을 거두었지만, 이전 기사에서 언급한 많은 문제와 과제 외에도 더 탐구할 가치가 있는 방향이 여전히 많이 있습니다.
그래프 신경망의 새로운 시나리오와 새로운 패러다임: 실제 세계에서는 행성의 중력부터 분자 상호작용까지 거의 모든 것이 어떤 관계로 연결된 것으로 볼 수 있으며, 그러면 모든 것이 그래프로 간주될 수 있습니다. 소셜 네트워크 분석부터 추천 시스템 및 자연 과학에 이르기까지 다양한 분야에서 그래프 신경망의 관련 응용 탐색과 지능형 교통의 시공간 상호 작용, 금융 위험 제어 시나리오의 다양한 범주와 같은 응용 문제로 인해 발생하는 모델 개발을 살펴보았습니다. 생화학 분야에서는 균형, 분석적 구조 판별 문제 등이 있습니다. 따라서 다양한 장면에서 장면 관련 특징을 어떻게 적응적으로 학습할 것인지가 여전히 중요한 방향입니다. 또한, 현재 GNN은 주로 메시지 전달 패러다임을 기반으로 정보 전송, 정보 집계, 정보 업데이트의 3단계를 사용하여 정보 전송, 집계 및 업데이트를 보다 합리적이고 효율적으로 만드는 방법이 있습니다. 현재 GNN 작업에 더 중요합니다. 반면에 메시지 전달 프레임워크와 분류적 가정으로 인해 발생하는 정보의 과도한 평활화 문제와 정보 병목 현상도 더 복잡한 데이터 및 시나리오에서 그 효과를 제한합니다. 전반적으로 대부분의 GNN은 항상 컴퓨터 비전과 자연어 처리에서 몇 가지 아이디어를 차용하지만 어떻게 차용 규칙을 깨고 그래프 데이터의 귀납적 선호도를 기반으로 보다 강력한 모델을 설계하고 그래프 신경망에 고유한 기능을 주입할 수 있을까요? soul 역시 해당 분야의 연구자들이 계속 고민하고 노력하는 방향이 될 것입니다.
그래프 구조 학습: 그래프 신경망과 기존 신경망의 주요 차이점은 그래프의 구조를 가이드로 사용하고 이웃 정보를 집계하여 노드 표현을 학습한다는 것입니다. 실제로 애플리케이션에는 그래프 구조가 정확하다는 기본 가정이 있습니다. 즉, 그래프의 연결이 실제적이고 신뢰할 수 있다는 것입니다. 예를 들어 소셜 그래프의 가장자리는 진정한 우정을 의미합니다. 그러나 실제로는 그래프의 구조가 그다지 신뢰도가 높지 않고, 시끄러운 연결과 우발적인 연결이 흔히 발생합니다. GNN의 잘못된 그래프 구조와 확산 과정은 노드 표현과 다운스트림 작업(가비지 인, 가비지 아웃)의 성능을 크게 저하시킵니다. 따라서 그래프 구조를 어떻게 더 잘 학습하고, 다양한 데이터 시나리오에서 보다 신뢰할 수 있는 그래프 구조를 구축할 수 있는지가 중요한 방향입니다.
신뢰할 수 있는 그래프 신경망: 정보 전송 메커니즘과 그래프 데이터의 비IID 특성으로 인해 GNN은 적대적 공격에 매우 취약하며 노드 특성 및 그래프 구조에서 적대적 교란에 쉽게 영향을 받습니다. . 예를 들어 사기꾼은 신용도가 높은 특정 사용자와 거래를 생성하여 GNN 기반 사기 탐지를 회피할 수 있습니다. 따라서 보안 위험이 높은 일부 영역에서는 강력한 그래프 신경망의 개발이 매우 필요합니다. 한편, 개인정보 보호에 대한 사회 전반의 관심이 높아지면서 최근 연구에서는 그래프 신경망의 공정성, 데이터 개인정보 보호에 대한 관심도 뜨겁다. 예를 들어, 2022년 알리바바 DAMO 아카데미의 그래프 데이터 연합 학습 오픈소스 플랫폼인 FederatedScope-GNN도 올해 KDD 2022에서 최우수 응용 논문상을 수상했습니다. 또한 모델 내 암시적 데이터를 보호한다는 목적(그래프 언러닝)을 달성하기 위해 훈련된 그래프 모델이 특정 데이터 훈련 효과/특정 매개변수를 잊어버리게 만드는 방법도 논의할 가치가 있는 방향입니다.
해석 가능성: 딥 러닝 모델은 많은 작업에서 기존 방법이 따라올 수 없는 성능을 달성했지만 모델의 복잡성으로 인해 해석 가능성이 제한되는 경우가 많습니다. 그러나 생물정보학, 건강, 금융 위험 제어 등 많은 고감도 분야에서 계산 모델을 평가하고 기본 메커니즘을 더 잘 이해할 때 해석 가능성이 중요합니다. 따라서 최근에는 해석 가능하거나 복잡한 관계를 더 잘 시각화할 수 있는 모델/아키텍처를 설계하는 것이 더 많은 관심을 끌고 있습니다. 기존 작업은 주로 텍스트와 이미지의 해석 가능성에 대한 방법을 언급합니다. 예를 들어 그라데이션 변경이나 입력 섭동을 기반으로 하는 방법(예: GNNExplainer)입니다. 최근 일부 연구자들은 불변 학습을 기반으로 그래프 신경망의 본질적인 설명 가능성을 더 잘 도출하고 그래프 모델의 설명 가능성에 대한 통찰력을 제공하기 위해 인과 선별 방법을 사용하여 설명 가능성 측정 프레임워크를 탐색하려고 시도했습니다.
분포 외 일반화: 일반적인 학습 문제는 훈련 세트에 대한 모델 훈련을 완료한 다음, 테스트 데이터 분포가 훈련과 크게 다른 경우 모델이 새로운 테스트 세트에 대한 결과를 제공해야 하는 것입니다. 분포, 모델의 일반화 오류를 제어하기가 어렵습니다. 대부분의 최신 그래프 신경망(GNN) 방법은 학습 그래프와 테스트 그래프 사이의 알 수 없는 편차를 고려하지 않으므로 OOD(Out-of-Distribution) 그래프에서 GNN의 일반화 성능이 저하됩니다. 그러나 실제로는 많은 시나리오에서 모델이 개방적이고 동적인 환경과 상호 작용해야 합니다. 학습 단계에서 모델은 추천 시스템의 새로운 사용자/항목, 새로운 항목과 같이 향후 알려지지 않은 분포의 새로운 엔터티 또는 샘플을 고려해야 합니다. 온라인 광고 시스템의 제품 등 플랫폼의 사용자 초상화/행동 특성, 동적 네트워크의 새로운 노드 또는 에지 관계 등 따라서 제한된 관찰 데이터를 어떻게 활용하여 알려지지 않았거나 제한된 데이터가 있는 새로운 환경에 일반화할 수 있는 안정적인 GNN 모델을 학습하는지도 중요한 연구 방향입니다.
그래프 데이터 사전 훈련 및 일반 모델: 사전 훈련 패러다임은 컴퓨터 비전 및 자연어 처리 분야에서 혁신적인 성공을 거두었으며 많은 작업에서 강력한 기능을 입증했습니다. GNN에는 이미 상대적으로 성숙한 모델과 성공적인 응용 프로그램이 있지만, 작업이 변경되거나 레이블이 충분하지 않은 경우 결과가 만족스럽지 못한 경우가 많으므로 대량의 레이블이 지정된 데이터를 사용하는 딥 러닝에만 국한됩니다. 따라서 자연스럽게 그래프 데이터 시나리오의 일반 모델에 대한 모든 사람의 탐색과 사고를 촉발합니다. 사전 훈련의 핵심은 풍부한 훈련 데이터, 전달 가능한 지식, 강력한 백본 모델 및 효과적인 훈련 방법에 있습니다. 컴퓨터 비전 및 자연어 처리의 명확한 의미 정보와 비교할 때 다양한 그래프 데이터 구조가 매우 다양하기 때문에 그래프의 어떤 지식을 전달할 수 있는지는 여전히 상대적으로 열려 있는 질문입니다. 또한 심층적이고 일반적인 GNN 모델이 연구되었지만 아직 혁명적인 개선을 가져오지 못했습니다. 다행스럽게도 그래프 머신러닝 커뮤니티에서는 대규모 그래프 데이터가 축적되어 있고 그래프 재구성과 같은 자가 지도 학습 방법을 개발했습니다. 심층적인 GNN, 보다 표현력이 뛰어난 GNN, 그래프 자체 감독의 새로운 패러다임에 대한 후속 연구를 통해 강력한 다양성을 갖춘 보편적인 모델이 결국 실현될 것으로 믿어집니다.
소프트웨어 및 하드웨어 협업: 그래프 학습의 응용 및 연구 개발이 발전함에 따라 GNN은 확실히 PyTorch, TensorFlow, Mindpsore 등과 같은 표준 프레임워크 및 플랫폼에 더욱 깊이 통합될 것입니다. 그래프 모델의 확장성을 더욱 향상시키기 위해 보다 하드웨어 친화적인 알고리즘 프레임워크와 소프트웨어로 조정되는 하드웨어 가속 솔루션이 일반적인 추세입니다. 그래프 신경망 애플리케이션을 위한 전용 가속 구조가 천천히 등장하고 있지만 그래프 신경망을 위한 컴퓨팅 하드웨어 장치 및 온칩 스토리지 계층 구조와 컴퓨팅 및 메모리 액세스 동작을 최적화하는 전용 칩을 사용자 정의하는 것은 어느 정도 성공을 거두었지만 이러한 기술은 아직 초기 단계에 있습니다. 거대한 도전에 직면하고 이에 따라 많은 기회를 제공합니다.
위 내용은 딥러닝의 토폴로지 미학: GNN 기초 및 적용의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7532
7532
 15
15
 1379
1379
 52
52
 82
82
 11
11
 55
55
 19
19
 21
21
 79
79
 Python에서 BERT를 사용한 감정 분석 방법 및 단계
Jan 22, 2024 pm 04:24 PM
Python에서 BERT를 사용한 감정 분석 방법 및 단계
Jan 22, 2024 pm 04:24 PM
BERT는 Google이 2018년에 제안한 사전 훈련된 딥러닝 언어 모델입니다. 전체 이름은 BidirectionEncoderRepresentationsfromTransformers이며 Transformer 아키텍처를 기반으로 하며 양방향 인코딩의 특성을 가지고 있습니다. 기존 단방향 코딩 모델과 비교하여 BERT는 텍스트를 처리할 때 상황 정보를 동시에 고려할 수 있으므로 자연어 처리 작업에서 잘 수행됩니다. 양방향성을 통해 BERT는 문장의 의미 관계를 더 잘 이해할 수 있어 모델의 표현 능력이 향상됩니다. 사전 훈련 및 미세 조정 방법을 통해 BERT는 감정 분석, 이름 지정 등 다양한 자연어 처리 작업에 사용될 수 있습니다.
 일반적으로 사용되는 AI 활성화 함수 분석: Sigmoid, Tanh, ReLU 및 Softmax의 딥러닝 실습
Dec 28, 2023 pm 11:35 PM
일반적으로 사용되는 AI 활성화 함수 분석: Sigmoid, Tanh, ReLU 및 Softmax의 딥러닝 실습
Dec 28, 2023 pm 11:35 PM
활성화 기능은 딥 러닝에서 중요한 역할을 하며 신경망에 비선형 특성을 도입하여 네트워크가 복잡한 입력-출력 관계를 더 잘 학습하고 시뮬레이션할 수 있도록 합니다. 활성화 함수의 올바른 선택과 사용은 신경망의 성능과 훈련 결과에 중요한 영향을 미칩니다. 이 기사에서는 일반적으로 사용되는 네 가지 활성화 함수인 Sigmoid, Tanh, ReLU 및 Softmax를 소개부터 시작하여 사용 시나리오, 장점, 단점과 최적화 솔루션은 활성화 기능에 대한 포괄적인 이해를 제공하기 위해 논의됩니다. 1. 시그모이드 함수 시그모이드 함수 공식 소개: 시그모이드 함수는 실수를 0과 1 사이에 매핑할 수 있는 일반적으로 사용되는 비선형 함수입니다. 통일하기 위해 자주 사용됩니다.
 잠재 공간 임베딩: 설명 및 시연
Jan 22, 2024 pm 05:30 PM
잠재 공간 임베딩: 설명 및 시연
Jan 22, 2024 pm 05:30 PM
잠재 공간 임베딩(LatentSpaceEmbedding)은 고차원 데이터를 저차원 공간에 매핑하는 프로세스입니다. 기계 학습 및 딥 러닝 분야에서 잠재 공간 임베딩은 일반적으로 고차원 입력 데이터를 저차원 벡터 표현 세트로 매핑하는 신경망 모델입니다. 이 벡터 세트를 "잠재 벡터" 또는 "잠재 벡터"라고 합니다. 인코딩". 잠재 공간 임베딩의 목적은 데이터의 중요한 특징을 포착하고 이를 보다 간결하고 이해하기 쉬운 형식으로 표현하는 것입니다. 잠재 공간 임베딩을 통해 저차원 공간에서 데이터를 시각화, 분류, 클러스터링하는 등의 작업을 수행하여 데이터를 더 잘 이해하고 활용할 수 있습니다. 잠재 공간 임베딩은 이미지 생성, 특징 추출, 차원 축소 등과 같은 다양한 분야에서 폭넓게 응용됩니다. 잠재공간 임베딩이 핵심
 ORB-SLAM3를 넘어! SL-SLAM: 저조도, 심한 흔들림, 약한 텍스처 장면을 모두 처리합니다.
May 30, 2024 am 09:35 AM
ORB-SLAM3를 넘어! SL-SLAM: 저조도, 심한 흔들림, 약한 텍스처 장면을 모두 처리합니다.
May 30, 2024 am 09:35 AM
이전에 작성했던 오늘은 딥 러닝 기술이 복잡한 환경에서 비전 기반 SLAM(동시 위치 파악 및 매핑)의 성능을 향상할 수 있는 방법에 대해 논의합니다. 심층 특징 추출과 깊이 일치 방법을 결합하여 저조도 조건, 동적 조명, 질감이 약한 영역 및 심한 지터와 같은 까다로운 시나리오에서 적응을 향상하도록 설계된 다목적 하이브리드 시각적 SLAM 시스템을 소개합니다. 우리 시스템은 확장 단안, 스테레오, 단안 관성 및 스테레오 관성 구성을 포함한 여러 모드를 지원합니다. 또한 시각적 SLAM을 딥러닝 방법과 결합하여 다른 연구에 영감을 주는 방법도 분석합니다. 공개 데이터 세트 및 자체 샘플링 데이터에 대한 광범위한 실험을 통해 위치 정확도 및 추적 견고성 측면에서 SL-SLAM의 우수성을 입증합니다.
 하나의 기사로 이해하기: AI, 머신러닝, 딥러닝 간의 연결과 차이점
Mar 02, 2024 am 11:19 AM
하나의 기사로 이해하기: AI, 머신러닝, 딥러닝 간의 연결과 차이점
Mar 02, 2024 am 11:19 AM
오늘날 급속한 기술 변화의 물결 속에서 인공지능(AI), 머신러닝(ML), 딥러닝(DL)은 정보기술의 새로운 물결을 이끄는 밝은 별과도 같습니다. 이 세 단어는 다양한 최첨단 토론과 실제 적용에 자주 등장하지만, 이 분야를 처음 접하는 많은 탐험가들에게는 그 구체적인 의미와 내부 연관성이 여전히 수수께끼에 싸여 있을 수 있습니다. 그럼 먼저 이 사진을 보시죠. 딥러닝, 머신러닝, 인공지능 사이에는 밀접한 상관관계와 진보적인 관계가 있음을 알 수 있습니다. 딥러닝은 머신러닝의 특정 분야이며, 머신러닝은
 기초부터 실습까지 Elasticsearch 벡터 검색의 개발 이력을 검토해보세요.
Oct 23, 2023 pm 05:17 PM
기초부터 실습까지 Elasticsearch 벡터 검색의 개발 이력을 검토해보세요.
Oct 23, 2023 pm 05:17 PM
1. 소개 벡터 검색은 현대 검색 및 추천 시스템의 핵심 구성 요소가 되었습니다. 복잡한 객체(예: 텍스트, 이미지, 사운드)를 수치 벡터로 변환하고 다차원 공간에서 유사성 검색을 수행하여 효율적인 쿼리 매칭 및 추천을 가능하게 합니다. 기초부터 실습까지 Elasticsearch의 개발 이력을 살펴보세요. 벡터 검색_elasticsearch 유명한 오픈 소스 검색 엔진으로서 Elasticsearch의 벡터 검색 분야 개발은 항상 많은 관심을 받아왔습니다. 본 글에서는 각 단계의 특징과 진행 상황을 중심으로 Elasticsearch 벡터 검색의 개발 역사를 검토해 보겠습니다. 기록을 가이드로 삼아 모든 사람이 전체 범위의 Elasticsearch 벡터 검색을 설정하는 것이 편리합니다.
 매우 강하다! 딥러닝 알고리즘 상위 10개!
Mar 15, 2024 pm 03:46 PM
매우 강하다! 딥러닝 알고리즘 상위 10개!
Mar 15, 2024 pm 03:46 PM
2006년 딥러닝이라는 개념이 제안된 지 거의 20년이 지났습니다. 딥러닝은 인공지능 분야의 혁명으로 많은 영향력 있는 알고리즘을 탄생시켰습니다. 그렇다면 딥러닝을 위한 상위 10가지 알고리즘은 무엇이라고 생각하시나요? 다음은 제가 생각하는 딥 러닝을 위한 최고의 알고리즘입니다. 이들은 모두 혁신, 애플리케이션 가치 및 영향력 측면에서 중요한 위치를 차지하고 있습니다. 1. 심층 신경망(DNN) 배경: 다층 퍼셉트론이라고도 불리는 심층 신경망(DNN)은 가장 일반적인 딥 러닝 알고리즘으로 처음 발명되었을 때 최근까지 컴퓨팅 성능 병목 현상으로 인해 의문을 제기했습니다. 20년, 컴퓨팅 파워, 데이터의 폭발적인 증가로 돌파구가 찾아왔습니다. DNN은 여러 개의 숨겨진 레이어를 포함하는 신경망 모델입니다. 이 모델에서 각 레이어는 입력을 다음 레이어로 전달하고
 단백질과 모든 살아있는 분자의 상호 작용과 구조를 이전보다 훨씬 더 정확하게 예측하는 AlphaFold 3 출시
Jul 16, 2024 am 12:08 AM
단백질과 모든 살아있는 분자의 상호 작용과 구조를 이전보다 훨씬 더 정확하게 예측하는 AlphaFold 3 출시
Jul 16, 2024 am 12:08 AM
Editor | Radish Skin 2021년 강력한 AlphaFold2가 출시된 이후 과학자들은 단백질 구조 예측 모델을 사용하여 세포 내 다양한 단백질 구조를 매핑하고 약물을 발견하며 알려진 모든 단백질 상호 작용에 대한 "우주 지도"를 그려 왔습니다. 방금 Google DeepMind는 단백질, 핵산, 소분자, 이온 및 변형된 잔기를 포함한 복합체에 대한 결합 구조 예측을 수행할 수 있는 AlphaFold3 모델을 출시했습니다. AlphaFold3의 정확도는 과거의 많은 전용 도구(단백질-리간드 상호작용, 단백질-핵산 상호작용, 항체-항원 예측)에 비해 크게 향상되었습니다. 이는 단일 통합 딥러닝 프레임워크 내에서 다음을 달성할 수 있음을 보여줍니다.




