Wanzi 분석을 활용한 자율주행 특징점 기반의 GPS 기술
자율 주행에서는 인식, 위치 지정, 계획 및 의사 결정, 제어가 4가지 기본 시스템 모듈입니다. 현재의 알고리즘으로는 절대지능을 달성할 수 없기 때문에 안전한 자율주행을 구현하기 위해서는 모듈 성능과 견고성을 향상시키기 위해 여전히 많은 양의 사전 지식이 필요합니다. 그 중 고정밀 지도는 도로와 주변 환경에 대한 사전 지식을 통합한 것입니다. 지도를 기반으로 한 정확한 위치 파악은 운전 상황을 판단하는 중요한 기반이며 이후의 인식 및 계획 결정에 강력한 지원을 제공합니다.
현재 위치 확인에 사용되는 주요 데이터 소스에는 GPS, 라이더, 비전, 밀리미터파 레이더가 포함됩니다. 비전의 경우 현재 업계에서 충분히 신뢰할 수 있는 측위 솔루션이 인정되지 않음에도 불구하고 이 분야에 대한 탐구는 멈추지 않았습니다. 주된 이유는 다음과 같습니다.
안전은 무인 운전 시스템의 가장 중요한 지표이므로 구현이 이루어집니다. 대부분의 기능 중 하나는 다중 소스 데이터와 다양한 알고리즘 결과를 결합하는 것입니다. 예를 들어, 널리 사용되는 솔루션인 GPS RTK는 위성 상태, 기상 조건, 데이터 링크 전송 상태에 쉽게 영향을 받으며 터널, 실내, 인구 밀집 지역에서는 사용할 수 없습니다. . 또한 LiDAR는 계산량이 적고 깊이 정보를 제공하며 조명의 영향을 받지 않는다는 장점이 있지만 정보가 희박하고 비용이 여전히 비싸며 대량의 차량을 조립할 수 있는 능력이 아직 없습니다. 이에 비해 카메라가 제공하는 시각적 정보는 조명과 날씨의 영향을 받지만 비용이 저렴하고 콘텐츠가 풍부하며 현재 운전 보조 솔루션의 주요 데이터 소스이며 지도 위치 파악에도 큰 잠재력을 가지고 있습니다.
주류 시각적 위치 확인 알고리즘의 핵심 아이디어는 동일하므로, 이 글에서는 실제로 가장 일반적으로 사용되는 특징점 기반 전역 위치 확인 알고리즘을 일련의 중요한 알고리즘 프레임워크 구성 요소의 관점에서 소개합니다. 지도 좌표계 위치를 지정합니다. 이 기사에서는 학생들에게 위치 결정 알고리즘에 대한 거시적 소개를 제공하기 위해 관련된 최적화 및 기하학적 제약 공식 도출을 생략했습니다. 관련 문헌 및 서적을 참조하십시오.
특징점의 전역 포지셔닝 알고리즘을 기반으로
시각적 전역 포지셔닝이란 현재 영상을 기준으로 지도 좌표계에서 카메라의 6자유도(DoF) 포즈(Pose)를 찾는 것을 말하며, is, (x, y, z) 좌표와 세 개의 좌표축을 중심으로 한 각도 편향(요, 피치, 롤)입니다. 현재는 크게 3차원 구조 기반 방법, 2차원 이미지 기반 방법, 시퀀스 이미지 기반 방법, 딥러닝 기반 방법으로 분류할 수 있다. 그 중 딥러닝을 기반으로 한 방법은 end-to-end 방법이고, 다른 multi-stage(Multi-stage) 비-end-to-end 방법은 프로세스가 다르지만, 알고리즘 아이디어는 대부분 그림 1과 같습니다. 표현:

그림 1: 쿼리 이미지를 기반으로 2D-3D 변환 행렬을 계산하고 카메라 포즈를 해결합니다.
구축된 지도를 기반으로 역사상 가장 유사한 지도 하위 집합과 일치 (이미지/포인트 클라우드/특징점), 일치된 지도 하위 집합에서 제공되는 실제 역사적 포즈 값과 특징점 좌표 실제 값을 기반으로 포인트 쌍 간의 변환 행렬을 계산하고 현재 카메라 포즈를 해결합니다.
그래서 핵심에는 이미지 설명, 매핑 쿼리, 기능 일치, 포즈 계산의 네 가지 측면이 포함됩니다. 이는 기술 수준의 거시적 분류일 뿐이며, 실제 알고리즘 프레임워크가 반드시 이 순서대로 실행되는 것은 아니며, 학자들은 주로 연구에서 이러한 기술을 개선하는 데 중점을 둡니다. 전반적으로 특징점을 기반으로 한 이미지 설명은 기본적으로 성숙하고 발전이 덜되었습니다. 포즈 계산은 기하학적 제약을 기반으로 하는 최적화 문제이므로 방법이 상대적으로 고정되어 있습니다. 대조적으로 쿼리 매핑 및 기능 일치에는 향상된 기술이 많이 있습니다. 데이터 소스에 따라 매핑 쿼리 및 일치는 2D-2D, 2D-3D 또는 3D-3D일 수 있습니다. 2D 이미지는 카메라로 얻고, 3D 포인트 클라우드는 깊이를 제공하는 쌍안경 카메라나 RGB-D 카메라로 생성할 수 있습니다.
특징점 추출
2D 이미지 자체는 밝기와 색상으로 구성된 매트릭스로 보는 각도, 조명, 색상 변화 등에 매우 민감하여 직접 사용하기가 매우 어렵습니다. 따라서 일반적으로 관련 계산에는 대표점이 사용됩니다. 사람들은 그러한 점이 회전, 이동, 크기 조정, 조명 불변성 등의 이점을 갖기를 바랍니다. 이러한 점을 키포인트와 설명자를 포함하여 이미지의 특징점이라고 합니다. 핵심 포인트는 특징점의 위치를 표현하는 반면 설명자는 특징점의 시각적 특성을 주로 벡터 형식으로 설명합니다. 일반적으로 설명자는 주로 특정 패턴의 핵심 포인트 주변의 회색조/색상 그라데이션 변화를 계산합니다. 강력한 디스크립터를 위해서는 동일한 특징점의 디스크립터의 거리(Distance)가 다른 이미지의 다른 상황에서 더 작아야 합니다.
설명어는 일반적으로 손으로 만든 기능입니다. 일반적인 설명에는 HOG(Histogram of Oriented Gradients)[1], SIFT(Scale-invariant Feature Transform)[2], SURF(Speeded up Robust Feature)[3], AKAZE(Accelerated KAZE)[4] 등이 포함됩니다.
실시간 요구 사항을 충족하기 위해 LBP(Local Binary Pattern)[5], BRIEF(Binary Robust Independent Elementary Feature), ORB(Oriented)와 같이 계산 속도가 더 빠른 일부 바이너리 패턴 설명자가 설계되었습니다. FAST 및 회전된 BRIEF)[6], BRISK(Binary Robust Invariant Scalable Key-Point)[7], FREAK(Fast Retina 키포인트)[8] 등
딥 러닝이 대중화되기 전에는 이러한 손으로 만든 기능이 전체 컴퓨팅 비전 산업을 주도해 왔으며 오늘날까지도 이러한 기능은 레이블이 지정된 데이터가 부족하고 제약 조건이 많은 시나리오에서 여전히 널리 사용됩니다. 다음은 일반적으로 사용되는 두 가지 설명에 대한 간략한 소개입니다.
SIFT
SIFT 디스크립터는 CV 세계에서 가장 영향력 있는 기술 중 하나로 간주될 수 있습니다. 핵심점 검출 관점에서 다중 스케일 공간의 극한점을 핵심점으로 검출하기 위해 DoG(Difference of Gaussian) 방법이 주로 사용됩니다. Babaud et al.은 가우스 평활화가 사용될 수 있는 유일한 다중 규모 공간 평활화 필터 커널임을 입증하여 관련 방법에 대한 충분한 이론적 지원을 제공했습니다.
그런 방법으로 왜 특징 핵심 포인트를 찾을 수 있을까요?
가우시안 커널은 블러를 통해 이미지를 다양한 스케일 공간으로 스케일링할 수 있고, 다양한 스케일 공간에서 작은 그라데이션 변화로 부드러운 영역의 값을 조정할 수 있기 때문입니다. 간격이 더 작습니다. 반대로 가장자리, 점, 모서리, 질감 등의 영역에서는 차이가 더 큽니다. 이와 같이 인접한 스케일의 이미지 간의 차이를 만들어 최종적으로 다중 스케일 공간의 극점을 계산할 수 있습니다. 그러나 서로 다른 이미지 세부 사항은 본질적으로 서로 다른 규모입니다. 예를 들어, 인물 사진에서 얼굴은 약간 흐릿해진 후 한 조각으로 스무딩될 수 있지만 프레임 모서리는 로컬 "극단 값"을 반영하기 위해 더 큰 규모의 스무딩이 필요할 수 있습니다.
따라서 그림 2와 같이 먼저 이미지 피라미드를 사용하여 이미지를 그룹화(Octave)하고 각 그룹마다 서로 다른 스케일의 가우시안 커널을 사용하여 일련의 레이어를 구성합니다. 이 방법은 단순히 더 많은 가우스 커널을 사용하는 것보다 낫고 더 많은 특징점을 감지할 수 있습니다. SIFT가 핵심 포인트 탐지를 위해 DoG를 사용하더라도 다른 탐지 방법도 가능하며 SIFT 설명자 설정에 영향을 미치지 않는다는 점에 유의해야 합니다.
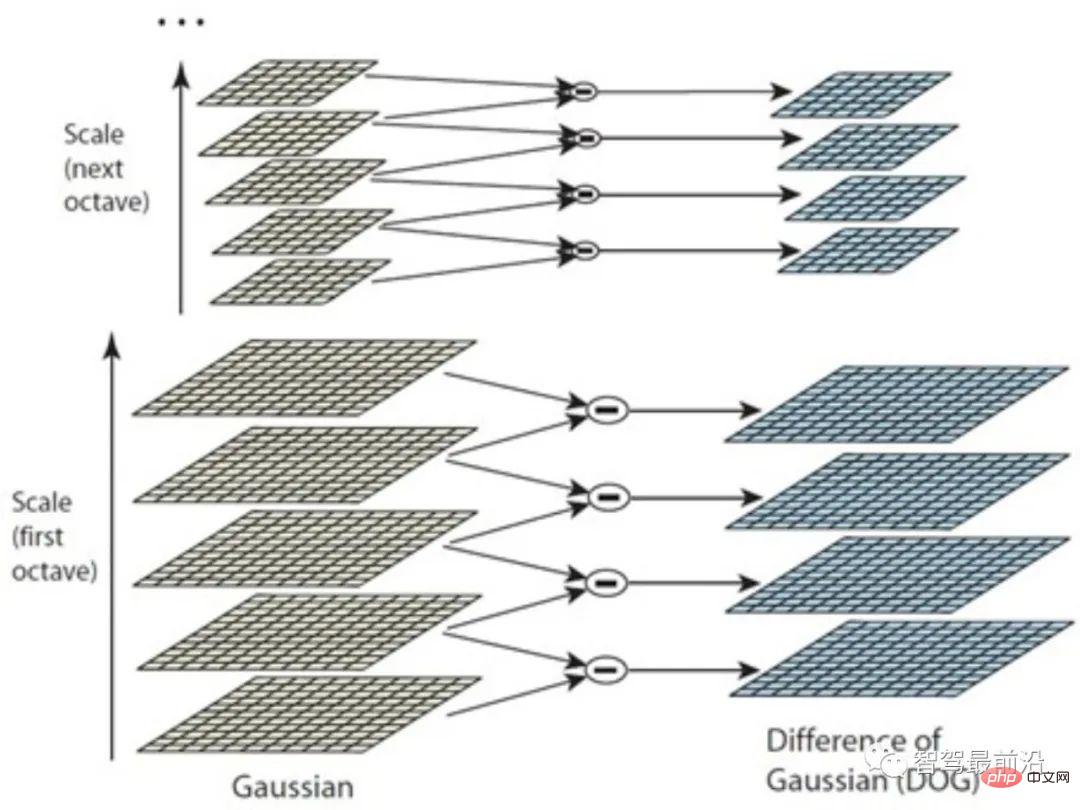
그림 2: 가우스 차이 방법
SIFT 특징점 설명자는 HOG의 간단한 통계 버전으로 이해될 수 있습니다. 그림 3과 같이 검출된 키포인트를 중심으로 주변의 16×16 영역을 선택하고 해당 영역을 4개의 4×4 패치로 재구성한다. 각 블록에 대해 8개 빈 히스토그램을 사용하여 그라데이션을 계산합니다. 그라데이션 방향에 따라 해당 블록이 속하는 빈이 결정되고, 그라데이션 모듈에 따라 값의 크기가 결정됩니다. 스케일 일관성을 보장하려면 그래디언트 크기를 정규화해야 합니다. 회전 불변성을 보장하기 위해 16×16 영역의 모든 기울기를 기준으로 주 방향을 계산하고 모든 기울기를 주 방향에 따라 회전시킵니다. 결과는 4 × 4 × 8 128차원 벡터입니다.
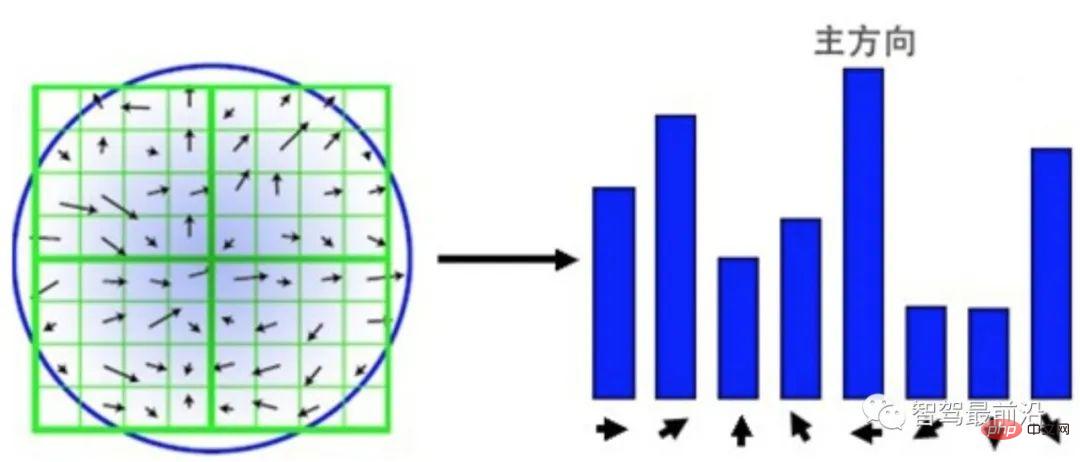
그림 3: 그래디언트 차단 통계를 기반으로 한 SIFT 설명자
이진 설명자
SIFT가 제안된 이후 SURF, AKAZE 등 일부 개선된 알고리즘이 제작되었지만 2019년 현재에도 일부 시나리오에서는 알고리즘의 실시간 요구 사항을 보장하기가 여전히 어렵습니다. 예를 들어, 휴대용 장치는 일반적으로 컴퓨팅 성능이 제한되어 있습니다. 자율 주행에서는 여러 컴퓨팅 집약적 모듈을 통해 CPU와 GPU 리소스를 동시에 예약해야 합니다. 따라서 효율성은 알고리즘의 실용성을 검토하는 중요한 지표입니다.
효율성을 높이기 위해 학자들은 일부 바이너리 설명자를 제안했습니다. 일반적으로 이러한 방법은 특징 핵심 포인트를 중심으로 포인트 샘플링을 수행합니다. 그런 다음 한 쌍의 점의 계조 크기를 비교하고 그 결과를 0/1로 표현하여 N차원 이진 설명 벡터를 형성하고 특징점의 이진 패턴을 형성합니다. 다양한 바이너리 설명자 간의 가장 큰 차이점은 주로 다양한 기능 샘플링 모드와 포인트 쌍 선택 방법에 있습니다.
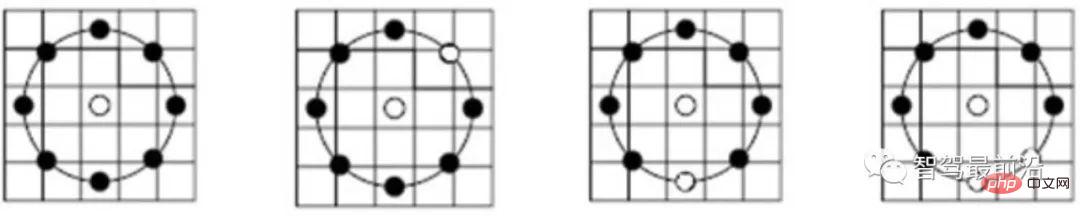
그림 4: LBP 설명자 서브 샘플링 모드
그림 4에서 볼 수 있듯이 LBP 설명자는 핵심 포인트 주변의 순환 샘플링을 채택하고 이를 중앙 핵심 포인트의 회색조와 비교합니다. . 회색조 비교 결과는 링에 표시되며 검은색 점은 0이고 흰색 점은 1입니다. LBP는 가장 간단한 형태의 바이너리 디스크립터인 반면, ORB는 BRIEF 기능을 개선하여 현재 일반적으로 사용되는 바이너리 디스크립터입니다. 그림 5와 같이 포인트 쌍을 선택할 때 ORB는 단순히 중심점을 사용하는 것과 달리 지역적 세부 사항을보다 포괄적으로 설명하기 위해 무작위 방법을 사용합니다. 그러나 포인트 쌍 간의 상관 관계는 상대적으로 크기 때문에 설명자의 식별력이 감소합니다. ORB는 이 문제를 해결하기 위해 탐욕스럽고 철저한 방법을 직접 사용하고 상관 관계가 낮은 임의의 포인트 쌍을 찾습니다.
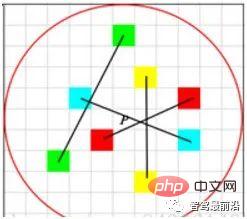
그림 5: ORB 디스크립터 포인트 쌍 선택 모드
위 바이너리 디스크립터의 샘플링 방법 및 포인트 쌍 선택 방법은 사람들의 일반적인 직관에 부합하는 반면, BRISK 및 FREAK와 같은 디스크립터는 스케일 정보가 내장된 보다 규칙적인 바이너리 패턴 구성 방법을 제안합니다. 예를 들어, FREAK 설명자는 인간 눈의 시각적 샘플링 패턴을 모방합니다. 그림 6에서 볼 수 있듯이 각 샘플링 포인트의 값은 빨간색 원 안의 평균 회색 값이며 파란색 선은 포인트 쌍 선택 계획을 나타냅니다.
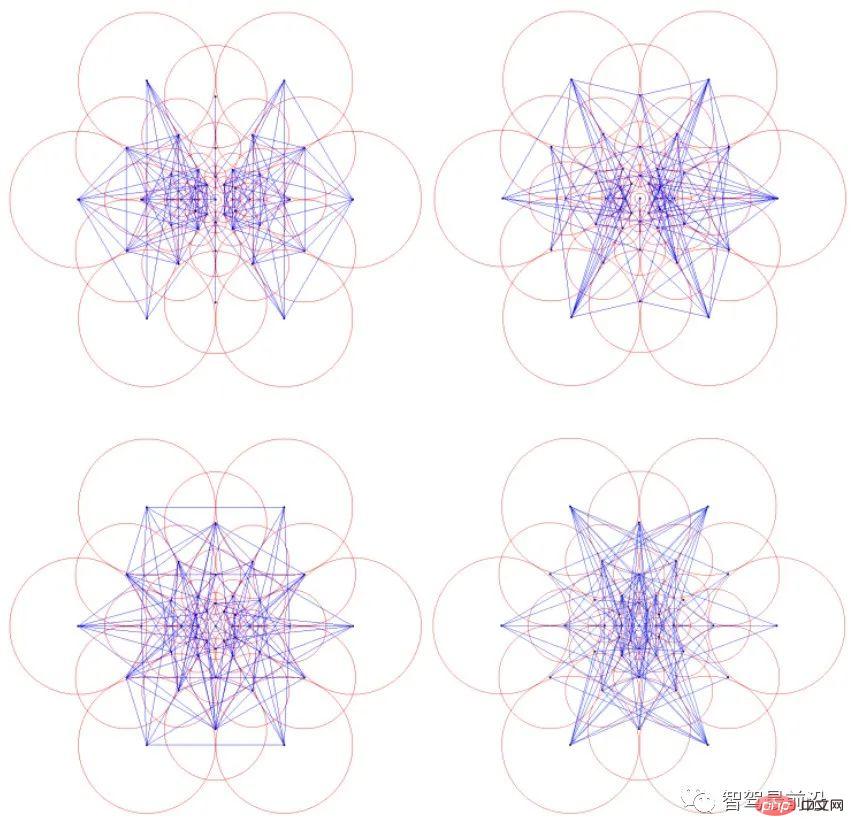
그림 6: FREAK 설명자 샘플링, 포인트 쌍 선택 모델
이진 설명자의 높은 효율성은 주로 세 가지 측면에서 반영됩니다.
(1) 이진 설명자는 특징 설명으로 이진 벡터를 사용하며 특정 그라데이션을 계산하지 않고 점 쌍의 크기만 비교하면 됩니다.
(2) 두 디스크립터 간의 비교에는 계산이 더 빠르고 최적화가 더 쉬운 해밍 거리(Hamming distance)를 사용할 수 있습니다.
(3) 각 이진 벡터는 십진수에 해당하므로 SIFT처럼 히스토그램을 사용하여 표시할 필요 없이 그 자체로도 패턴을 나타냅니다.
이진 설명자는 일반적으로 SIFT 제품군 설명자만큼 차별적이지는 않지만 특정 시나리오에서는 병렬 프로그래밍과 결합하면 유사한 판별 기능을 보장하면서 효율성이 수십 또는 수백 배 더 높아질 수 있습니다.
데이터베이스 생성 및 쿼리
데이터베이스는 맵 + 인덱스의 통합으로 이해될 수 있습니다. 맵은 순수 2D 이미지, 3D 포인트 클라우드 맵 또는 2D 이미지와 3D 포인트 클라우드의 조합으로 구성될 수 있습니다. 3차원 포인트 클라우드 맵 생성은 주로 3차원 재구성 방법인 SfM(Structure from Motion)을 사용하여 시계열 2차원 영상에서 3차원 정보를 추론합니다. 쌍안 RGB-D 카메라가 심도를 제공한다면 보다 정확한 3D 포인트 정보를 얻을 수 있습니다. 또한 키프레임과 같은 일부 선택 전략도 포함되어 있습니다. 구체적인 방법은 이 기사의 범위를 벗어납니다. 관심 있는 학생들은 스스로 관련 정보를 확인할 수 있습니다. 데이터베이스의 역할은 다음과 같습니다.
입력 관측 이미지의 경우 데이터베이스를 통해 매핑 기록(이미지/포인트 클라우드/특징 포인트)을 쿼리하여 가장 가능성이 높은 지도 하위 집합(이미지/포인트 클라우드)을 얻습니다. 현재 영상/특징점에서 관찰된 것), 지도를 관찰 정보와 일치시키고 변환 행렬을 계산하여 관찰 카메라의 자세를 구합니다.
색인은 이 프로세스의 속도를 높이는 열쇠입니다. 데이터베이스 자체는 거대한 경향이 있습니다. 베이징 조양시 조이시티 2층에 있는 메이투안 파우치 로봇의 시범 운영을 예로 들어보자. 3대의 심도 카메라가 설치된 이후에도 거의 8만 장의 900×600 사진이 사용됐다. 측위의 실시간 특성을 고려할 때 80,000개의 이미지에 대한 쿼리를 매번 하나씩 비교하는 것은 불가능하므로 전체 알고리즘의 속도를 높이려면 인덱싱 기술을 사용해야 합니다. 이 기술은 SLAM의 루프백 테스트, 이미지 검색 및 비전의 위치 인식과 많이 중복됩니다. 아래에서는 일반적인 방법만 소개합니다.
이미지에는 VLAD(로컬 집계 설명자의 벡터) 인코딩과 같이 먼저 특징점을 인코딩해야 하는 여러 특징점이 있으며, 로컬 설명자는 이미지의 전역 설명을 형성하는 데 사용됩니다. 그런 다음 kd-tree와 같은 인덱스를 사용하여 이미지 수준 쿼리를 수행합니다. 물론 계층적 단어백 모델(Bag-of-words, BoW) + 순방향 인덱스 + 역방향 인덱스 방식 등 인코딩과 인덱싱을 동시에 수행할 수도 있습니다.
VLAD 인코딩
VLAD(Vector of Locally Aggregated Descriptors)[10]은 그림 7과 같이 로컬 디스크립터들을 집합하고 누적을 통해 디스크립션을 계산하여 형성된 코드북(Codebook)이다. 서브워드와 코드워드(Word) 사이는 전역 인코딩을 위한 간단한 방법입니다. 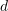 차원 설명자
차원 설명자  는
는 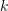 코드워드의 코드북을 통해 인코딩되어
코드워드의 코드북을 통해 인코딩되어 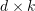 차원 설명 벡터를 형성합니다. 벡터의 값은 설명자와
차원 설명 벡터를 형성합니다. 벡터의 값은 설명자와 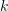 번째 코드워드의 차이입니다.
번째 코드워드의 차이입니다. 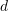 차원. 그런 다음
차원. 그런 다음 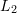 정규화가 수행되어 최종 VLAD 벡터를 형성합니다.
정규화가 수행되어 최종 VLAD 벡터를 형성합니다.
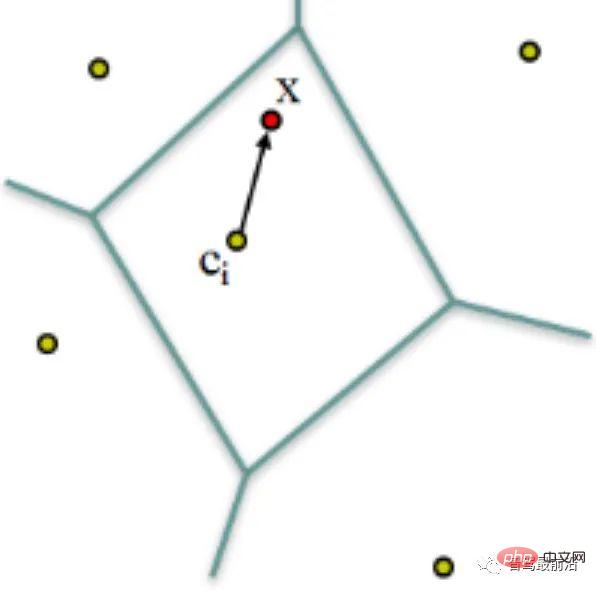
그림 7: VLAD는 설명자와 코드 워드
DenseVLAD[11] 및 NetVLAD[12] 사이의 거리로 인코딩됩니다. Torii 등은 DenseSIFT가 쿼리, 매칭 모두에서 표준 SIFT보다 성능이 우수하다는 것을 입증했습니다. DenseVLAD는 2픽셀 간격의 격자형 샘플링 패턴으로 4가지 스케일에서 SIFT 포인트를 추출합니다. 전역적으로 2,500만 개의 설명자를 무작위로 샘플링하고 k-평균 알고리즘을 사용하여 128개 코드워드의 코드북을 생성합니다. VLAD 벡터는 정규화 후 PCA(주성분 분석)를 사용하여 차원적으로 감소되어 최종 4096차원 DenseVLAD 벡터를 형성합니다. 그림 8에서 볼 수 있듯이 DenseSIFT를 사용하여 매칭한 후 내부 점(녹색)의 수가 더 많습니다.

그림 8: DenseSIFT 및 표준 SIFT 특징점, 일치 후 내부 점(녹색) 비교
NetVLAD는 VLAD 인코딩의 식별성을 높이기 위해 VLAD에 감독 정보를 추가합니다. 그림 9에서 볼 수 있듯이 두 설명자 red와 green은 서로 일치해서는 안 되는 두 그림에서 나온다고 가정합니다. 둘 다 더 큰 반경에 있고 VLAD 중심(×)으로부터 비슷한 거리에 있기 때문에 L2 정규화 후에는 인코딩된 값이 매우 유사합니다. 빨간색과 녹색 설명자에 해당하는 그림이 일치하지 않는다는 감시 정보를 추가한 후 NetVLAD에서 생성된 중심점(★)은 두 설명자를 더 잘 구별하고 인코딩된 거리(반경) 차이를 늘릴 수 있습니다. [ 13, 14] 코딩과 그에 따른 디자인 아이디어는 컴퓨터 비전의 발전에 결정적인 역할을 하기 때문에 여기서는 소개하지 않겠습니다. 이 기사에서는 일반적인 BoW 인코딩 및 인덱싱 통합 모델을 소개하기 위해 2D 이미지 데이터베이스와 일치하는 2D 쿼리 이미지를 예로 사용합니다. 그림 10에 도시된 바와 같이, 데이터 세트의 모든 설명어에 대해 계층적 방법을 사용하여 사전(Vocabulary)을 생성하고, 트리 구조에 따라 공간을 구분하고 각 계층을 k-평균 클러스터링으로 계산합니다. 최종 리프 노드는 코드 단어와 동일합니다(그림 10에는 9개의 코드 단어가 있습니다).
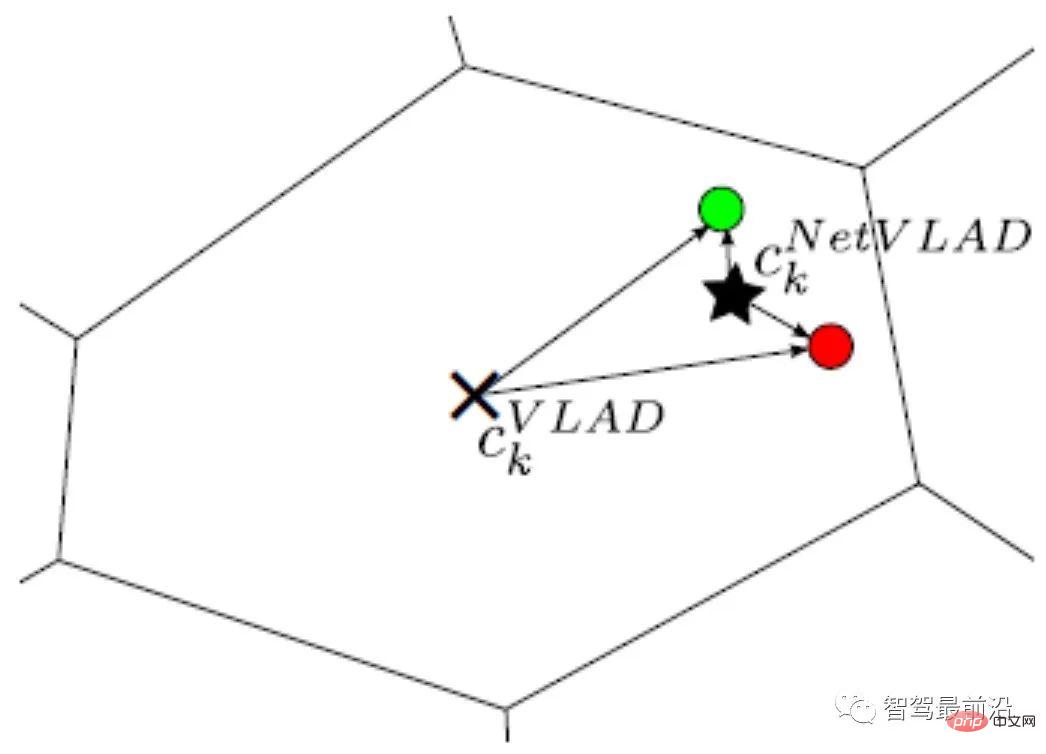
그림 10: 순방향 인덱스와 역방향 인덱스가 있는 계층적 BoW 모델 트리 구성 프로세스는 실제로 원본 이미지를 인코딩하는 프로세스입니다. 그러나 인코딩 자체는 검색 속도를 높이지는 않지만 VLAD와 유사하게 데이터베이스의 이미지와 하나씩 비교해야 합니다. 따라서 여기서는 인코딩된 벡터를 비교할 필요가 없는 역 인덱스(Inverse index)를 설계합니다. 그 원리는 그림 11과 같다. 쿼리 이미지(Query image)의 경우, 추출된 디스크립터는 BoW에 입력되고 결국 코드워드 리프 노드(Visual word) k에 속하게 된다. 각 코드 단어는 인덱스에 해당하며 데이터베이스 의
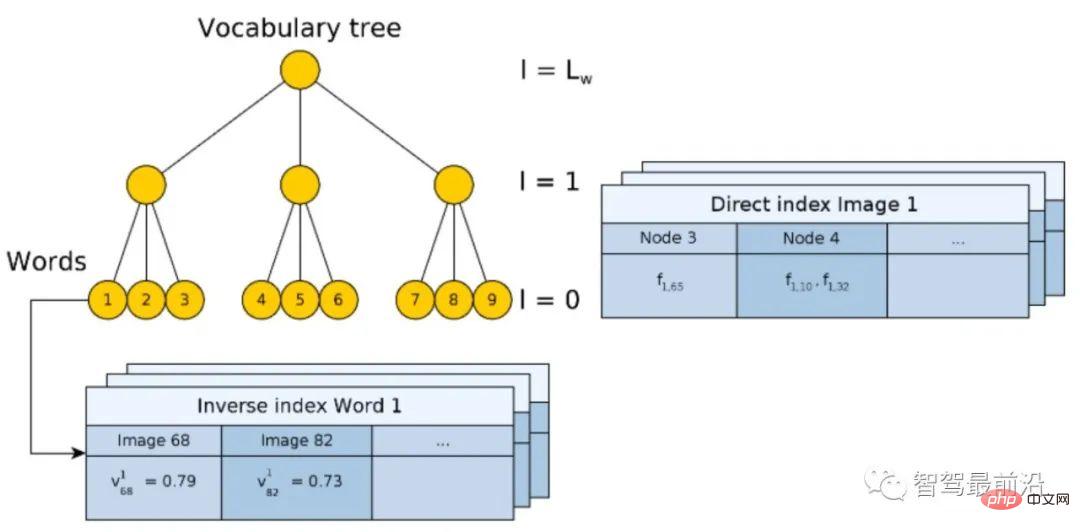 번째 그림에 대한 코드 단어
번째 그림에 대한 코드 단어
의 가중치를 기록합니다(그림 10). 여기서 가중치는 TF-IDF(용어 빈도-역 문서 빈도)를 사용하여 계산됩니다. 즉, 단어 가 특정 이미지
에 자주 나타나고 다른 이미지에서는 빈도가 낮다면 이 단어는 이미지 식별성이 더 좋고 가중치 값이 더 높습니다 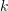 . 마지막으로 투표 메커니즘을 통해 일치하는 이미지가 선택됩니다. 역방향 인덱스는 반드시 트리 구조의 BoW에 구축되는 것은 아니며, 단지 빠른 쿼리 방법을 제공할 뿐이라는 점을 기억하는 것도 중요합니다.
. 마지막으로 투표 메커니즘을 통해 일치하는 이미지가 선택됩니다. 역방향 인덱스는 반드시 트리 구조의 BoW에 구축되는 것은 아니며, 단지 빠른 쿼리 방법을 제공할 뿐이라는 점을 기억하는 것도 중요합니다. 
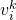
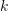 그림 11: 역색인 + 투표 메커니즘을 통해 이미지 직접 쿼리
그림 11: 역색인 + 투표 메커니즘을 통해 이미지 직접 쿼리 
Direct Index의 주요 기능은 BoW를 구성할 때 데이터베이스 이미지의 특징점이 어떤 노드에 속하는지 기록하는 것입니다. 이렇게 하면 이미지를 쿼리할 때 특징점을 계산할 필요가 없으며, 색인 추출 특징점을 직접 사용할 수 있습니다.
3D 포인트 클라우드 쿼리
2D 이미지 쿼리에서는 먼저 의미 수준에서 이미지를 쿼리하므로 특징점의 공간 범위를 이미지를 통해 제한할 수 있습니다. 3D 포인트 클라우드 쿼리에는 이러한 제약이 없기 때문에 어려움이 많습니다. 공간 연속성을 고려해야 하는 경우, 쿼리된 모든 지점이 관측 가능한 범위 내에 있는지 여부 등 여기서는 Sattler가 TPAMI 2016[15]에서 발표한 방법만 소개합니다. 수년간의 개선을 거쳐 이 방법 프레임워크는 비교적 간단하고 완전합니다. 사전 인코딩 검색 단계는 이전 섹션의 내용과 겹치므로 여기서는 활성 검색과 가시성 필터링이라는 두 가지 메커니즘만 소개합니다.
Active Search는 주로 일치하는 3D 점을 공간에서 최대한 가깝게 만들고 기하학적 의미를 갖는 것입니다. 그림 12에 도시된 바와 같이, 빨간색 점은 일련의 인코딩 및 정제 과정(빨간색 선)을 통해 포인트 클라우드의 한 점과 일치됩니다. 제안된 우선순위 프레임워크에 따르면 포인트 클라우드에서 확률이 가장 높은 3D 포인트를 찾고, 쿼리 이미지의 해당 2D 포인트와 역방향(파란색 선)이 일치합니다.

그림 12: 능동 검색 일치하는 지점을 카메라에서 최대한 관찰할 수 있도록 하기 위해(위치 지정은 감독되지 않으며 일치하는 지점이 올바른지 알 수 없습니다). 여기서 채택한 방법은 SfM을 사용하여 3차원 포인트 클라우드 맵을 생성할 때 이분 가시성 그래프를 생성하는 것입니다. 그림 13(왼쪽)과 같이 두 대의 카메라로 동시에 한 지점을 관찰할 수 있으면 위상학적 관계가 성립됩니다. 그림 13(가운데)에서 파란색 점은 일치하는 점이며 관찰 관점에서 충돌합니다. 기존 토폴로지를 기반으로 그래프 클러스터링을 수행하면 그림 13(오른쪽)과 같이 카메라가 두 그룹으로 그룹화됩니다. 이러한 방식으로 새로운 그래프 토폴로지 관계가 생성될 수 있습니다. 그런 다음 각 하위 그래프 간의 중첩을 판단하여 보이지 않을 가능성이 높은 지점을 필터링합니다.
양안 카메라와 RGB-D 카메라는 깊이를 얻을 수 있고 2D 이미지를 쿼리하면 제한된 범위 내에서 3D 특징점 좌표를 얻을 수도 있지만 현재의 기술적 한계로 인해 실내 재료가 복잡하고 실외가 크다는 점에 유의해야 합니다. 규모가 큰 장면에서는 깊이가 신뢰할 수 없습니다. 따라서 2차원 이미지 포인트와 3차원 포인트 클라우드 맵의 매칭은 여전히 중요한 방법이다. 
특징점 매칭특징점 매칭 프로세스는 데이터베이스 쿼리에서 적응적으로 완료될 수 있으며, 이는 3D 구조 기반 쿼리에서 더 일반적입니다. 쿼리 후에 매칭을 별도로 수행할 수도 있는데, 이는 2D 이미지 기반 쿼리에서 더 일반적입니다. 특징 매칭의 목적은 포즈 계산을 달성하기 위한 후속 변환 행렬 계산을 위한 매칭 포인트 쌍을 제공하는 것입니다.
Classic RANSAC
Random Sample Consensus Algorithm(RANSAC)[16]은 고전적인 데이터 필터링 및 매개변수 피팅 알고리즘입니다. 데이터(인라이어)의 분포가 특정 수학적 모델을 따른다고 가정하고 반복적인 계산을 통해 아웃라이어와 노이즈 포인트를 제거하는 동시에 확률 측면에서 가장 좋은 모델 매개변수를 얻습니다. 전역 위치 지정에서 내부 점은 올바른 일치를 나타내고 외부 점은 잘못된 일치를 나타내며 매개변수 모델은 일치된 점 쌍의 공간 변환 행렬을 나타냅니다. 그림 14에서 볼 수 있듯이 RANSAC 알고리즘으로 최적화한 후 매칭이 더 합리적입니다. RANSAC이 찾을 것으로 예상하는 일치 부분 집합은 두 가지 지표를 충족해야 합니다. 즉, 내부 점 재투영 오류는 가능한 한 작고, 내부 점의 수는 최대한 큽니다. 따라서 기본 과정은 다음과 같습니다.
① 초기 부분 집합을 샘플링합니다.
② 변환 행렬을 계산합니다.
③ 변환 행렬에 따라 일치점의 재투영 오차를 계산합니다.
IV 큰 오류가 있는 점 제거
⑤ ① - ④를 반복하여 지수에 가장 잘 맞는 일치 솔루션을 유지합니다.

그림 14: (상) 원본 특징 매칭, (하) RANSAC 알고리즘에 의해 최적화된 매칭
그 중 초기 후보 매칭은 디스크립터 간의 거리를 기준으로 생성되지만 재투영되는 오류는 다음과 같습니다. 핵심 포인트의 공간적 위치에만 관련되며 설명자 자체와는 아무 관련이 없습니다. 구체적인 투영 행렬 방법은 "2.4 포즈 계산"을 참조하십시오. RANSAC 알고리즘은 원래 일치 오류 및 매개변수 선택의 영향을 받는다는 점을 지적해야 합니다. 이는 알고리즘이 합리적일 만큼 충분히 높은 확률을 보장할 수 있을 뿐이지만 반드시 최적의 결과를 얻을 수는 없습니다. 알고리즘 매개변수에는 주로 임계값과 반복 횟수가 포함됩니다. RANSAC이 신뢰할 수 있는 모델을 얻을 확률은 반복 횟수에 정비례하고, 얻은 일치 횟수는 임계값에 반비례합니다. 따라서 실제 사용 시 더 나은 결과를 얻으려면 다양한 매개변수 설정을 반복적으로 시도해야 할 수도 있습니다.
학자들은 고전적인 RANSAC 알고리즘을 많이 개선했습니다. 그림 15에서 볼 수 있듯이 거의 모든 RANSAC 개선 사항을 포괄하는 범용 RANSAC 아키텍처를 형성하는 글로벌 RANSAC(Universal-RANSAC)[17]의 구조 다이어그램이 제안되었습니다. 사전 필터링, 최소 하위 집합 샘플링, 최소 하위 집합에서 신뢰할 수 있는 모델 생성, 매개변수 검증, 모델 개선 등이 있습니다.
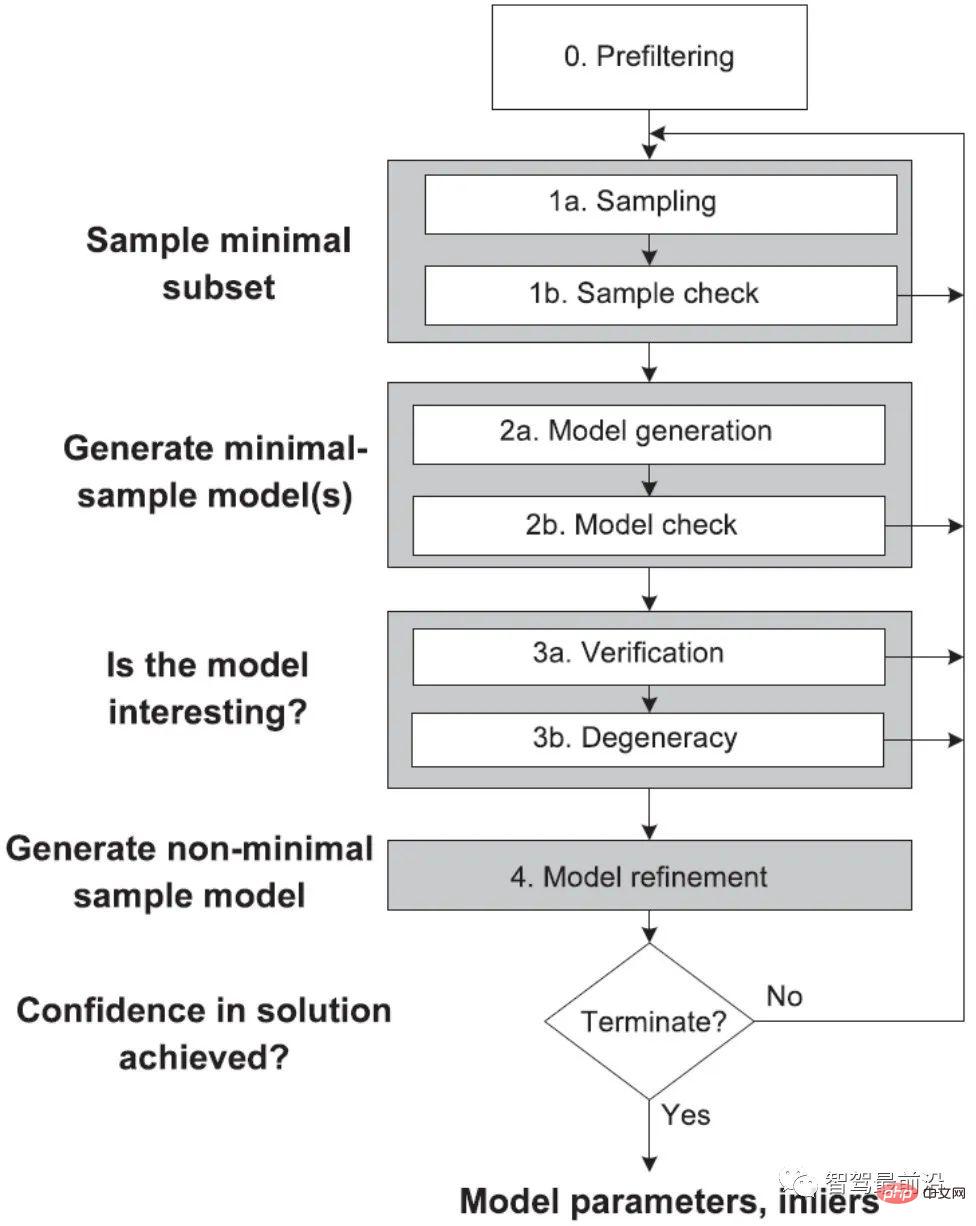
그림 15: Universal-RANSAC 일반 알고리즘 프레임워크
미분 가능한 RANSAC
수동 설명자가 위치 지정 분야에서 여전히 높은 성능을 보여주기 때문에 일부 학자들은 깊은 기존 방법을 완전히 대체하기 위해 엔드투엔드 포즈 추정 모델을 직접 사용하는 대신 알고리즘 프레임워크의 특정 부분을 대체하는 방법을 학습합니다. DSAC(Differentiable RANSAC)[18]는 결정론적 가설 선택을 확률론적 가설 선택으로 대체하여 RANSAC 프로세스가 도출될 수 있도록 하는 것을 목표로 합니다. 이 프로세스는 그림 16에 표시되며, 여기서 "Scoring" 단계는 여전히 재투영 오류를 사용합니다. 지표의 차이점은 특징점이 아닌 전체 이미지를 기준으로 오차가 발생하고, 기존 특징점 매칭을 선별하는 과정을 카메라 포즈 가설 h를 확률로 직접 선별하는 과정으로 대체한다는 점이다. 현재 방법에는 상대적으로 큰 제한이 있지만 DSAC는 현재 비지도 위치 확인 알고리즘 프레임워크에 사전 지식을 추가하는 방법에 대한 실행 가능한 아이디어를 제공합니다. 

그림 16: 차동 RANSAC 알고리즘 프레임워크
자세 계산
획득된 올바른 일치점 쌍을 위해 해당 변환 행렬은 기하학적 제약 조건을 통해 계산되어야 합니다( 변환 행렬) . 데이터베이스 내의 포인트 좌표와 샘플링 당시의 카메라 포즈를 알고 있으므로 해당 포인트의 변환 행렬을 맵 포인트와 일치시켜 현재 카메라 포즈를 얻을 수 있습니다. 여기에는 몇 가지 기본 기호가 정의되어 있습니다. 카메라의 내부 매개변수는  이고, 변환 순간의 동질적 형태
이고, 변환 순간의 동질적 형태  는 다음과 같습니다.
는 다음과 같습니다.

그 중 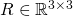 은 회전 행렬이고
은 회전 행렬이고 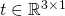 은 변환 행렬입니다. .
은 변환 행렬입니다. .
2.4.1 2D-2D 변환 행렬 계산
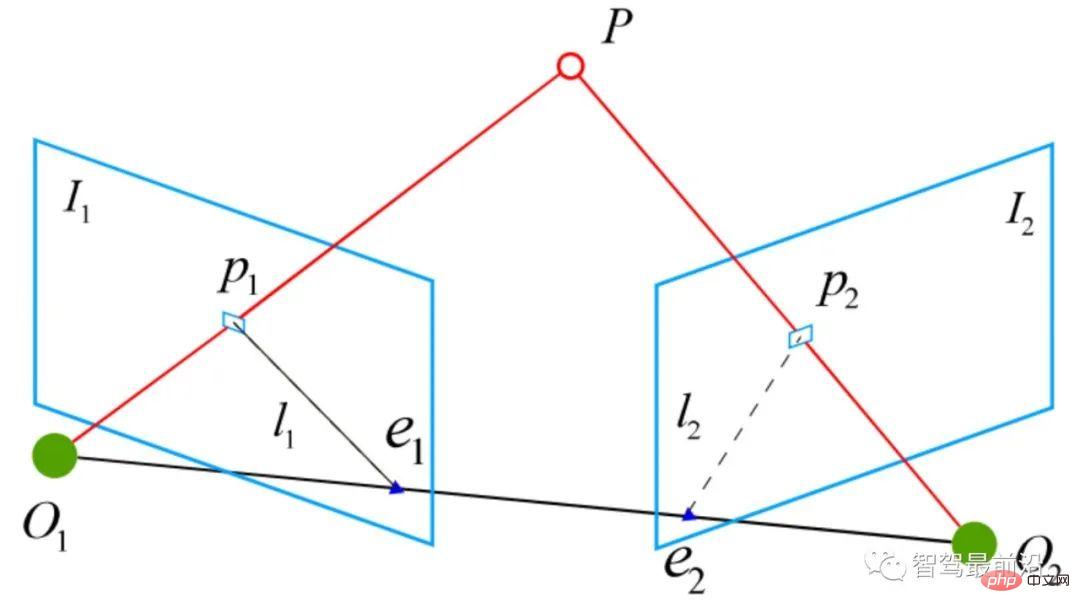
그림 17: 2D-2D 변환 행렬 계산의 에피폴라 기하학
두 개의 2차원 이미지에서 일치하는 특징점의 경우 ( 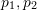 ), 정규화된 평면의 좌표는 (
), 정규화된 평면의 좌표는 (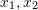 )이며 해당 변환 행렬은 에피폴라 제약 조건을 통해 계산되어야 합니다. 그림 17에서 볼 수 있듯이, 그 기하학적 의미는
)이며 해당 변환 행렬은 에피폴라 제약 조건을 통해 계산되어야 합니다. 그림 17에서 볼 수 있듯이, 그 기하학적 의미는 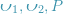 이 3개의 동일 평면이라는 것입니다. 이 표면을 극면이라고도 하고,
이 3개의 동일 평면이라는 것입니다. 이 표면을 극면이라고도 하고, 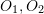 을 기준선,
을 기준선, 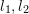 을 극선이라고 합니다. 에피폴라 제약 조건에는 다음과 같이 정의되는 평행 이동과 회전이 모두 포함됩니다.
을 극선이라고 합니다. 에피폴라 제약 조건에는 다음과 같이 정의되는 평행 이동과 회전이 모두 포함됩니다.

여기서 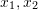 은 정규화된 평면에서
은 정규화된 평면에서 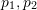 의 좌표이고 ∧는 외부 곱 연산자입니다. 공식의 중간 부분을 기본 행렬
의 좌표이고 ∧는 외부 곱 연산자입니다. 공식의 중간 부분을 기본 행렬 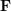 과 필수 행렬
과 필수 행렬 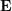 으로 계산하면 다음과 같습니다.
으로 계산하면 다음과 같습니다.

필수 행렬 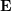 에는 스케일 정보가 없으므로 E에 0이 아닌 상수를 곱한 후에도 에피폴라 제약 조건은 여전히 유지됩니다.
에는 스케일 정보가 없으므로 E에 0이 아닌 상수를 곱한 후에도 에피폴라 제약 조건은 여전히 유지됩니다. 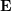 는 고전적인 8점 알고리즘(8점 알고리즘)으로 풀 수 있고 분해되어
는 고전적인 8점 알고리즘(8점 알고리즘)으로 풀 수 있고 분해되어 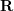 ,
, 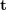 을 얻을 수 있습니다. 따라서 2D-2D 변환 행렬 해법 방법에는 두 가지 단점이 있음을 알 수 있다. 첫째, 단안시에는 규모의 불확실성이 있고, 초기화 시
을 얻을 수 있습니다. 따라서 2D-2D 변환 행렬 해법 방법에는 두 가지 단점이 있음을 알 수 있다. 첫째, 단안시에는 규모의 불확실성이 있고, 초기화 시 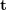 에 의해 규모 정보를 제공해야 한다. 이에 따라 단안 초기화는 순수한 회전일 수 없으며 충분한 수준의 변환이 있어야 합니다. 그렇지 않으면
에 의해 규모 정보를 제공해야 한다. 이에 따라 단안 초기화는 순수한 회전일 수 없으며 충분한 수준의 변환이 있어야 합니다. 그렇지 않으면 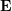 가 0이 됩니다.
가 0이 됩니다.
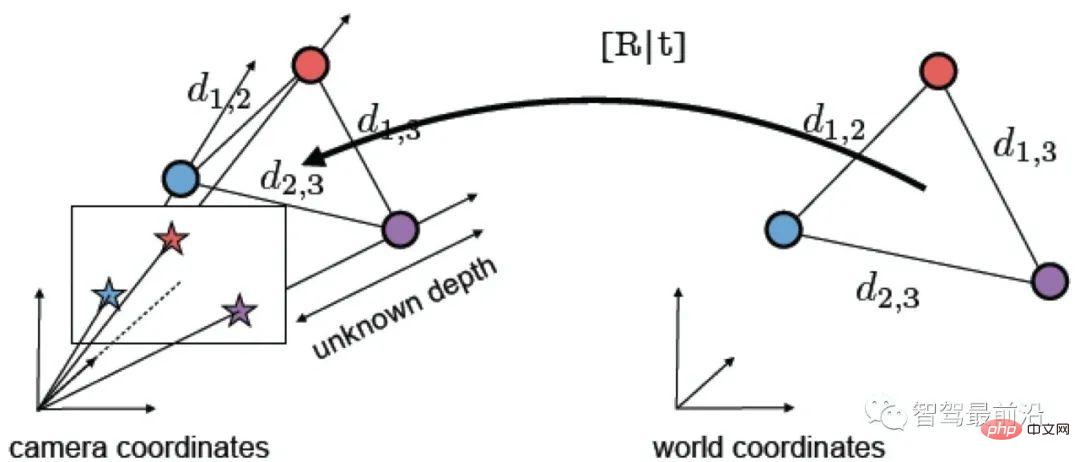
2.4.2 2D-3D 변환 행렬 계산
2D-3D 매칭은 포즈 추정에서 중요한 방법입니다. 일반적으로 PnP 방식을 사용하는데, 즉 2D-3D 매칭점을 알고 변환 행렬을 풀어 카메라 포즈를 구하는 방식이다. 3D 포인트 P(X, Y, Z)를 카메라 이미징 평면( )에 투영합니다.
)에 투영합니다. 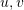
 여기서
여기서
은 스케일이고  입니다. 이 방정식의 해는 선형 방정식 문제로 축소될 수 있으며 각 기능은 두 가지 선형 제약 조건을 제공할 수 있습니다.
입니다. 이 방정식의 해는 선형 방정식 문제로 축소될 수 있으며 각 기능은 두 가지 선형 제약 조건을 제공할 수 있습니다. 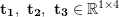
 이 방법으로 최소 6쌍의 일치점을 풀 수 있으며, 일치 항목이 6보다 크면 사용할 수 있습니다. SVD와 같은 방법은 최소 제곱을 구성하여 해결됩니다. P3P 방법은 그림 18과 같이 삼각형의 유사성 특성을 이용하여 더 많은 제약 조건을 추가하고 문제를 해결하기 위해 3쌍의 점만 필요로 하는 PnP 방법의 특별한 솔루션이라고 볼 수 있습니다. 다른 해결 방법으로는 DLT(Direct Linear Transformation), EPnP(Efficient PnP) 방법, UPnP(Uncalibrated PnP) 등이 있습니다. 위의 선형 최적화 방법과 비교하여 BA(BlubleAdjustment)와 같은 비선형 최적화 방법도 널리 사용됩니다. BA 방법은 시각적 SLAM의 일종의 "일률적"입니다. 동시에 여러 변수를 최적화할 수 있으므로 관심 있는 학생들은 로컬 오류로 인한 시스템 불안정성을 어느 정도 완화할 수 있습니다. 더 깊이 있는 이해를 위한 관련 정보.
이 방법으로 최소 6쌍의 일치점을 풀 수 있으며, 일치 항목이 6보다 크면 사용할 수 있습니다. SVD와 같은 방법은 최소 제곱을 구성하여 해결됩니다. P3P 방법은 그림 18과 같이 삼각형의 유사성 특성을 이용하여 더 많은 제약 조건을 추가하고 문제를 해결하기 위해 3쌍의 점만 필요로 하는 PnP 방법의 특별한 솔루션이라고 볼 수 있습니다. 다른 해결 방법으로는 DLT(Direct Linear Transformation), EPnP(Efficient PnP) 방법, UPnP(Uncalibrated PnP) 등이 있습니다. 위의 선형 최적화 방법과 비교하여 BA(BlubleAdjustment)와 같은 비선형 최적화 방법도 널리 사용됩니다. BA 방법은 시각적 SLAM의 일종의 "일률적"입니다. 동시에 여러 변수를 최적화할 수 있으므로 관심 있는 학생들은 로컬 오류로 인한 시스템 불안정성을 어느 정도 완화할 수 있습니다. 더 깊이 있는 이해를 위한 관련 정보.
3D-3D 변환 행렬 계산
3D 점 간의 변환 행렬은 ICP(반복적 최근점) 알고리즘을 사용하여 풀 수 있습니다. 점 쌍 일치( 또는 비선형 최적화 방법인 번들 조정 기반 거짓말 대수를 사용하여 을 해결할 수 있습니다. 여기서 ICP 문제는 고유한 해결책과 무한한 해결책이 있음이 입증되었습니다. 따라서 고유한 솔루션이 있는 경우 최적화 함수는 볼록 함수와 동일하며 최소값은 어떤 종류의 초기화를 채택하더라도 이 고유한 솔루션을 얻을 수 있습니다. 이것이 ICP 방식의 가장 큰 장점 중 하나입니다. 이 글에서는 이미지 설명, 매핑 쿼리, 특징 매칭, 포즈 계산의 네 가지 측면에서 특징점 기반 포즈 추정 알고리즘을 소개합니다. 전통적인 시각적 전역 위치 확인 방법은 여전히 실제 응용 분야에서 첫 번째 선택이지만, 전통적인 방법은 특징점이 올바르게 정의되고, 올바르게 추출되고, 올바르게 일치되고, 올바르게 관찰된다는 전제를 기반으로 합니다. 그 자체가 엄청난 도전이다. 둘째, 전통적인 방법은 end-to-end가 아닌 다단계 프레임워크이기 때문에 각 링크와 링크 간의 상호 작용에는 수많은 매개변수 조정이 필요하며, 각 링크의 기술은 별도의 연구 방향으로 사용될 수 있습니다. 실제 적용에서는 특정 시나리오에 해당하는 많은 트릭을 추가해야 하므로 엔지니어링이 더욱 복잡해집니다. 그리고 end-to-end 방식에 대한 사람들의 기대로 인해 PoseNet, VLocNet, HourglassNet 등과 같은 네트워크가 생겨나 벤치마크에서 좋은 결과를 얻었습니다. 저자는 현재의 end-to-end 방법에는 여전히 많은 문제가 있다고 생각합니다. 주된 문제는 손실 함수에 기하학적 제약이 부족하고, 맵을 구성할 때 포즈의 6자유도 공간이 연속적이지 않다는 것입니다. 입력 공간과의 좋은 매핑을 형성하기 어렵고 해당 위치 회귀, 미세 조정 메커니즘 등이 부족합니다. 비선형 공간에 대한 가장 강력한 모델링 도구로서 향후 포지셔닝 분야에서 딥러닝이 더욱 많이 등장할 것이라는 점은 부인할 수 없습니다. 시각적 위치 지정 자체로 돌아가 보겠습니다. 비전의 가장 중요한 장점은 저렴한 비용, 풍부한 의미 체계, 사용 시나리오에 대한 제한이 거의 없기 때문입니다. 따라서 비전에 초점을 맞추고 다른 저가형 센서를 보완한 위치결정 융합 솔루션도 앞으로 중요한 화두가 될 것이다. 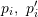 ) 결과가 정확하다고 가정하면 얻은 변환 행렬은 재투영 오류
) 결과가 정확하다고 가정하면 얻은 변환 행렬은 재투영 오류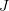 를 최소화해야 합니다. SVD를 사용하여 최소 제곱 문제를 해결할 수 있습니다:
를 최소화해야 합니다. SVD를 사용하여 최소 제곱 문제를 해결할 수 있습니다: 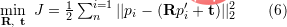
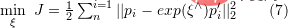
 은 카메라 포즈를 나타냅니다. 여기서 최적화 목표는 2D-3D 매칭의 번들 조정 목표와 유사하지만 원본 이미지의 2D 포인트가 카메라 이미징 평면에서 쌍안경을 통해 이동되었기 때문에 카메라 내부 매개변수를 고려할 필요가 없습니다
은 카메라 포즈를 나타냅니다. 여기서 최적화 목표는 2D-3D 매칭의 번들 조정 목표와 유사하지만 원본 이미지의 2D 포인트가 카메라 이미징 평면에서 쌍안경을 통해 이동되었기 때문에 카메라 내부 매개변수를 고려할 필요가 없습니다  카메라 또는 RGB-D 깊이 카메라를 3D 세계에 투영합니다.
카메라 또는 RGB-D 깊이 카메라를 3D 세계에 투영합니다.
위 내용은 Wanzi 분석을 활용한 자율주행 특징점 기반의 GPS 기술의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7338
7338
 9
9
 1627
1627
 14
14
 1352
1352
 46
46
 1265
1265
 25
25
 1210
1210
 29
29
 자율주행 분야에서 Gaussian Splatting이 인기를 끌면서 NeRF가 폐기되기 시작한 이유는 무엇입니까?
Jan 17, 2024 pm 02:57 PM
자율주행 분야에서 Gaussian Splatting이 인기를 끌면서 NeRF가 폐기되기 시작한 이유는 무엇입니까?
Jan 17, 2024 pm 02:57 PM
위에 작성됨 및 저자의 개인적인 이해 3DGS(3차원 가우스플래팅)는 최근 몇 년간 명시적 방사선장 및 컴퓨터 그래픽 분야에서 등장한 혁신적인 기술입니다. 이 혁신적인 방법은 수백만 개의 3D 가우스를 사용하는 것이 특징이며, 이는 주로 암시적 좌표 기반 모델을 사용하여 공간 좌표를 픽셀 값에 매핑하는 NeRF(Neural Radiation Field) 방법과 매우 다릅니다. 명시적인 장면 표현과 미분 가능한 렌더링 알고리즘을 갖춘 3DGS는 실시간 렌더링 기능을 보장할 뿐만 아니라 전례 없는 수준의 제어 및 장면 편집 기능을 제공합니다. 이는 3DGS를 차세대 3D 재구성 및 표현을 위한 잠재적인 게임 체인저로 자리매김합니다. 이를 위해 우리는 처음으로 3DGS 분야의 최신 개발 및 관심사에 대한 체계적인 개요를 제공합니다.
 자율주행 시나리오에서 롱테일 문제를 해결하는 방법은 무엇입니까?
Jun 02, 2024 pm 02:44 PM
자율주행 시나리오에서 롱테일 문제를 해결하는 방법은 무엇입니까?
Jun 02, 2024 pm 02:44 PM
어제 인터뷰 도중 롱테일 관련 질문을 해본 적이 있느냐는 질문을 받아서 간략하게 요약해볼까 생각했습니다. 자율주행의 롱테일 문제는 자율주행차의 엣지 케이스, 즉 발생 확률이 낮은 가능한 시나리오를 말한다. 인지된 롱테일 문제는 현재 단일 차량 지능형 자율주행차의 운영 설계 영역을 제한하는 주요 이유 중 하나입니다. 자율주행의 기본 아키텍처와 대부분의 기술적인 문제는 해결되었으며, 나머지 5%의 롱테일 문제는 점차 자율주행 발전을 제한하는 핵심이 되었습니다. 이러한 문제에는 다양한 단편적인 시나리오, 극단적인 상황, 예측할 수 없는 인간 행동이 포함됩니다. 자율 주행에서 엣지 시나리오의 "롱테일"은 자율주행차(AV)의 엣지 케이스를 의미하며 발생 확률이 낮은 가능한 시나리오입니다. 이런 희귀한 사건
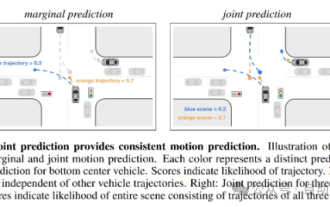 자율주행과 궤도예측에 관한 글은 이 글이면 충분합니다!
Feb 28, 2024 pm 07:20 PM
자율주행과 궤도예측에 관한 글은 이 글이면 충분합니다!
Feb 28, 2024 pm 07:20 PM
자율주행 궤적 예측은 차량의 주행 과정에서 발생하는 다양한 데이터를 분석하여 차량의 향후 주행 궤적을 예측하는 것을 의미합니다. 자율주행의 핵심 모듈인 궤도 예측의 품질은 후속 계획 제어에 매우 중요합니다. 궤적 예측 작업은 풍부한 기술 스택을 보유하고 있으며 자율 주행 동적/정적 인식, 고정밀 지도, 차선, 신경망 아키텍처(CNN&GNN&Transformer) 기술 등에 대한 익숙함이 필요합니다. 시작하기가 매우 어렵습니다! 많은 팬들은 가능한 한 빨리 궤도 예측을 시작하여 함정을 피하기를 희망합니다. 오늘은 궤도 예측을 위한 몇 가지 일반적인 문제와 입문 학습 방법을 살펴보겠습니다. 관련 지식 입문 1. 미리보기 논문이 순서대로 되어 있나요? A: 먼저 설문조사를 보세요, p
 카메라 또는 LiDAR를 선택하시겠습니까? 강력한 3D 객체 감지 달성에 대한 최근 검토
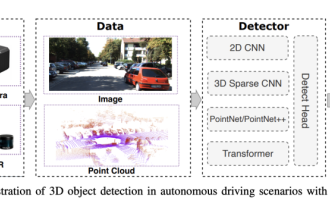
Jan 26, 2024 am 11:18 AM
카메라 또는 LiDAR를 선택하시겠습니까? 강력한 3D 객체 감지 달성에 대한 최근 검토
Jan 26, 2024 am 11:18 AM
0. 전면 작성&& 자율주행 시스템은 다양한 센서(예: 카메라, 라이더, 레이더 등)를 사용하여 주변 환경을 인식하고 알고리즘과 모델을 사용하는 고급 인식, 의사결정 및 제어 기술에 의존한다는 개인적인 이해 실시간 분석과 의사결정을 위해 이를 통해 차량은 도로 표지판을 인식하고, 다른 차량을 감지 및 추적하며, 보행자 행동을 예측하는 등 복잡한 교통 환경에 안전하게 작동하고 적응할 수 있게 되므로 현재 널리 주목받고 있으며 미래 교통의 중요한 발전 분야로 간주됩니다. . 하나. 하지만 자율주행을 어렵게 만드는 것은 자동차가 주변에서 일어나는 일을 어떻게 이해할 수 있는지 알아내는 것입니다. 이를 위해서는 자율주행 시스템의 3차원 객체 감지 알고리즘이 주변 환경의 객체의 위치를 포함하여 정확하게 인지하고 묘사할 수 있어야 하며,
 Stable Diffusion 3 논문이 드디어 공개되고, 아키텍처의 세부 사항이 공개되어 Sora를 재현하는 데 도움이 될까요?
Mar 06, 2024 pm 05:34 PM
Stable Diffusion 3 논문이 드디어 공개되고, 아키텍처의 세부 사항이 공개되어 Sora를 재현하는 데 도움이 될까요?
Mar 06, 2024 pm 05:34 PM
StableDiffusion3의 논문이 드디어 나왔습니다! 이 모델은 2주 전에 출시되었으며 Sora와 동일한 DiT(DiffusionTransformer) 아키텍처를 사용합니다. 출시되자마자 큰 화제를 불러일으켰습니다. 이전 버전과 비교하여 StableDiffusion3에서 생성된 이미지의 품질이 크게 향상되었습니다. 이제 다중 테마 프롬프트를 지원하고 텍스트 쓰기 효과도 향상되었으며 더 이상 잘못된 문자가 표시되지 않습니다. StabilityAI는 StableDiffusion3이 800M에서 8B 범위의 매개변수 크기를 가진 일련의 모델임을 지적했습니다. 이 매개변수 범위는 모델이 많은 휴대용 장치에서 직접 실행될 수 있어 AI 사용이 크게 줄어든다는 것을 의미합니다.
 SIMPL: 자율 주행을 위한 간단하고 효율적인 다중 에이전트 동작 예측 벤치마크
Feb 20, 2024 am 11:48 AM
SIMPL: 자율 주행을 위한 간단하고 효율적인 다중 에이전트 동작 예측 벤치마크
Feb 20, 2024 am 11:48 AM
원제목: SIMPL: ASimpleandEfficientMulti-agentMotionPredictionBaselineforAutonomousDriving 논문 링크: https://arxiv.org/pdf/2402.02519.pdf 코드 링크: https://github.com/HKUST-Aerial-Robotics/SIMPL 저자 단위: Hong Kong University of Science 및 기술 DJI 논문 아이디어: 이 논문은 자율주행차를 위한 간단하고 효율적인 모션 예측 기준선(SIMPL)을 제안합니다. 기존 에이전트 센트와 비교
 nuScenes의 최신 SOTA | SparseAD: Sparse 쿼리는 효율적인 엔드투엔드 자율주행을 지원합니다!
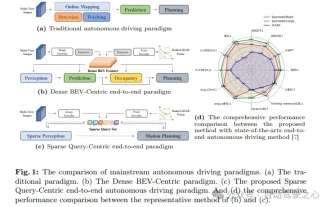
Apr 17, 2024 pm 06:22 PM
nuScenes의 최신 SOTA | SparseAD: Sparse 쿼리는 효율적인 엔드투엔드 자율주행을 지원합니다!
Apr 17, 2024 pm 06:22 PM
전면 및 시작점 작성 엔드 투 엔드 패러다임은 통합 프레임워크를 사용하여 자율 주행 시스템에서 멀티 태스킹을 달성합니다. 이 패러다임의 단순성과 명확성에도 불구하고 하위 작업에 대한 엔드투엔드 자율 주행 방법의 성능은 여전히 단일 작업 방법보다 훨씬 뒤떨어져 있습니다. 동시에 이전 엔드투엔드 방법에서 널리 사용된 조밀한 조감도(BEV) 기능으로 인해 더 많은 양식이나 작업으로 확장하기가 어렵습니다. 여기서는 희소 검색 중심의 엔드 투 엔드 자율 주행 패러다임(SparseAD)이 제안됩니다. 여기서 희소 검색은 밀집된 BEV 표현 없이 공간, 시간 및 작업을 포함한 전체 운전 시나리오를 완전히 나타냅니다. 특히 통합 스파스 아키텍처는 탐지, 추적, 온라인 매핑을 포함한 작업 인식을 위해 설계되었습니다. 게다가 무겁다.
 엔드투엔드(End-to-End)와 차세대 자율주행 시스템, 그리고 엔드투엔드 자율주행에 대한 몇 가지 오해에 대해 이야기해볼까요?
Apr 15, 2024 pm 04:13 PM
엔드투엔드(End-to-End)와 차세대 자율주행 시스템, 그리고 엔드투엔드 자율주행에 대한 몇 가지 오해에 대해 이야기해볼까요?
Apr 15, 2024 pm 04:13 PM
지난 달에는 몇 가지 잘 알려진 이유로 업계의 다양한 교사 및 급우들과 매우 집중적인 교류를 가졌습니다. 교환에서 피할 수 없는 주제는 자연스럽게 엔드투엔드와 인기 있는 Tesla FSDV12입니다. 저는 이 기회를 빌어 여러분의 참고와 토론을 위해 지금 이 순간 제 생각과 의견을 정리하고 싶습니다. End-to-End 자율주행 시스템을 어떻게 정의하고, End-to-End 해결을 위해 어떤 문제가 예상되나요? 가장 전통적인 정의에 따르면, 엔드 투 엔드 시스템은 센서로부터 원시 정보를 입력하고 작업과 관련된 변수를 직접 출력하는 시스템을 의미합니다. 예를 들어 이미지 인식에서 CNN은 기존의 특징 추출 + 분류기 방식에 비해 end-to-end 방식으로 호출할 수 있습니다. 자율주행 작업에서는 다양한 센서(카메라/LiDAR)로부터 데이터를 입력받아




