애니메이션 제작 효율이 80% UP! 이 AI 소프트웨어는 원클릭으로 고정밀 비디오 모션 캡처를 실현합니다.
AIGC에 새로운 마법이 생겼어요!
애니메이터의 손K가 필요하지 않으며, 습관 캡처나 빛 캡처도 필요하지 않습니다. 동영상만 제공하면 이 AI 모션 캡처 소프트웨어가 자동으로 동작을 출력합니다. 단 몇 분만에 가상인간의 애니메이션이 완성됩니다.

팔다리의 대형 프레임 움직임뿐만 아니라 손의 디테일까지 정확하게 포착할 수 있습니다.
단일 보기 비디오 외에도 다중 보기 비디오도 지원할 수 있습니다. 단안 인식만 지원하는 다른 모션 캡처 소프트웨어에 비해 이 소프트웨어는 더 높은 모션 캡처 품질을 제공할 수 있습니다.

동시에 소프트웨어는 인식된 인체 핵심 포인트, 부드러움, 발자국 세부 정보 등의 편집 및 수정도 지원합니다. 일반 플레이어의 관심 경험부터 하드코어 플레이어의 전문적인 요구까지 모든 것을 만족시킬 수 있습니다.
이것은 NetEase Interactive Entertainment AI Lab에서 수년 동안 개발한 AIxPose 비디오 모션 캡처 소프트웨어로, 전문적인 아트 피드백을 기반으로 지속적으로 반복적으로 최적화되고 로우 키입니다. 해당 소프트웨어는 수십 시간이 넘는 영상 리소스를 처리했으며 게임 플롯 애니메이션, 인기 댄스 애니메이션 및 기타 리소스 제작 과정에 사용된 것으로 알려졌다. 1분짜리 댄스 애니메이션을 손으로 제작하려면 20일 이상이 소요될 수 있지만, AIxPose 지원으로 제작하는 데는 3일밖에 걸리지 않으며, 전체 과정이 80% 이상 단축된다는 것이 실제 프로젝트를 통해 검증되었습니다.
최근 NetEase Interactive Entertainment AI Lab에서는 이 소프트웨어의 개발 경험과 모션 캡처 분야의 관련 연구 성과를 집대성하여 작성한 논문 "Learning Analytical Posterior Probability for Human Mesh Recovery"를 출판했습니다. CVPR 2023의 컴퓨터 비전 승인.

- 홈페이지 주소: https://netease-gameai.github.io/ProPose/
- 논문 주소: https://netease-gameai.github.io/ProPose/static /assets/CVPR2023_ProPose.pdf
본 논문은 단일 이미지, 다중 센서 융합 등 다양한 설정에서 정확한 3차원 이미지를 얻을 수 있는 사후 확률 기반 비디오 모션 캡처 기술 ProPose를 혁신적으로 제안합니다. 견적. 기술적 정확도는 사전 분석을 사용한 기준 확률적 방법보다 19% 더 높으며, 공개 데이터 세트 3DPW, Human3.6M 및 AGORA에서 과거 방법보다 성능이 뛰어납니다. 또한 다중 센서 융합 작업의 경우 이 기술은 새로운 센서 도입으로 인해 신경망의 백본을 수정하지 않고도 기본 모델보다 더 높은 정확도를 달성할 수도 있습니다.
기술적 배경
본 연구의 과제는 RGB 이미지로부터 HMR(Human Mesh Recovery)을 예측하는 것입니다. 기존 방법은 직접 방법과 간접 방법의 두 가지 범주로 요약할 수 있습니다. 직접 방법은 신경망을 사용하여 인간 관절의 엔드투엔드 회전 표현(예: 축 각도, 회전 행렬, 6D 벡터 등)을 회귀하는 반면, 간접 방법은 먼저 일부 중간 표현(예: 3차원 표현)을 예측합니다. 차원의 핵심 포인트, 세분화 등)을 수행한 후 이러한 중간체를 통과하여 관절 회전이 획득되었음을 나타냅니다.
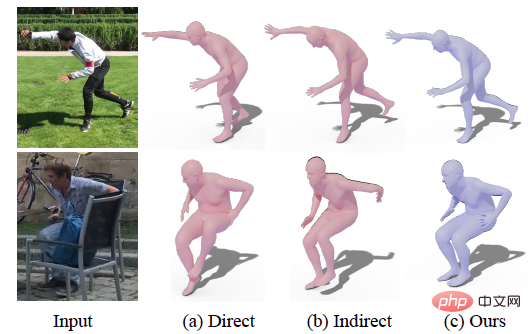
그러나 두 가지 방법 모두 몇 가지 문제가 있습니다. 직접 방법의 경우 이러한 유형의 방법은 네트워크가 회전과 같은 추상 표현을 직접 학습해야 하기 때문에 핵심 사항 및 분할 학습에 비해 회전 학습이 상대적으로 어렵기 때문에 네트워크에서 출력되는 결과가 이미지와 일치하기 어려운 경우가 있습니다. 아래 그림(a)의 첫 번째 행에 있는 오른발과 같은 일부 큰 동작은 뒤로 완전히 뻗을 수 없습니다. 대조적으로, 간접 방법은 일반적으로 더 높은 정확도를 생성하지만 이러한 유형의 방법의 성능은 중간 표현의 정확성에 크게 의존합니다. 중간 표현이 노이즈로 인해 오류를 생성하는 경우 최종 회전이 매우 명확해지기 쉽습니다. 아래 (b)의 두 번째 줄 왼쪽에 표시된 대로 오류가 발생합니다.
앞서 언급한 결정론적 방법 외에도 특정 확률 분포를 학습하여 인간 자세의 불확실성을 모델링함으로써 소음을 고려하고 시스템 견고성을 향상시키는 몇 가지 방법도 있습니다. 현재 주요 확률 모델링 방법에는 다변량 가우스 분포, 정규화된 흐름, 신경망 암시적 모델링 등이 포함되지만 non-SO(3)에 대한 이러한 확률 분포는 관절 회전의 불확실성을 실제로 반영할 수 없습니다. 예를 들어, 불확실성이 큰 경우 SO(3)에 대한 가우스 분포의 로컬 선형성 가정이 유지되지 않습니다. 최근 연구에서는 행렬 Fisher 분포의 매개변수를 학습하기 위해 네트워크를 직접 사용했습니다. 이는 SO(3)에 대한 분포이지만 이 방법의 학습 방법은 직접 방법과 유사하며 수렴 성능은 수렴 성능을 비교할 수 없습니다. 기존 간접 방식.
높은 정확성과 견고성을 모두 고려하고 확률적 방법의 성능을 향상시키기 위해 ProPose는 관절 회전의 분석적 사후 확률을 도출합니다. 이는 다양한 관찰 변수로 인한 높은 정확성의 이점을 누릴 수 있을 뿐만 아니라 불확실성을 측정하고 노이즈가 알고리즘에 미치는 영향을 최대한 줄입니다. 아래 그림과 같이 입력 영상에 대해 ProPose는 출력 확률 분포를 통해 다양한 방향의 관절 회전의 불확실성을 어느 정도 측정할 수 있습니다. 왼팔이 위아래로 흔들리는 정도, 왼쪽 종아리의 거리 정도 등.
기술적 구현
인체 모델링
이 연구의 목표는 뼈 방향과 같은 일부 관찰된 변수의 조건에서 관절 회전 R의 후방을 찾는 것입니다. d 등) 확률 p(R|d,⋯).
구체적으로 인체의 관절 회전은 SO(3)에 위치하고, 부모 관절을 기준으로 한 자식 관절의 단위 뼈 방향은 S^2에 위치하므로 확률을 기반으로 할 수 있습니다. 이 두 다양체에 대한 분포를 분석합니다.
먼저, SO(3)에 대한 행렬 Fisher 분포 MF(⋅)는 다음 공식 F∈R^(3×3)과 같이 관절 회전 R의 사전 분포로 사용될 수 있습니다. 는 이 분포의 매개변수이고, c(F)는 정규화 상수이고, tr은 행렬의 자취를 나타냅니다.
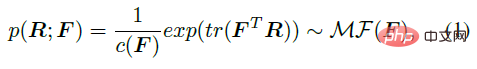
다음 수식에서 볼 수 있듯이 F는 평균 M과 SVD 분해를 통해 분포 집계 정도를 나타내는 집계 항 K에 대해 직접 풀 수 있습니다. 그 중 Δ=diag(1,1,|UV|)는 대각 직교행렬로, M의 행렬식을 1로 하여 특수 직교군에 속할 수 있도록 하기 위해 사용된다.
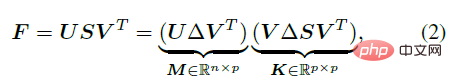
둘째, 관절 회전을 통해 뼈의 방향을 계산할 수 있다는 점을 고려하면 관절 회전 R은 은닉 변수로, 뼈 방향 d는 관찰 변수로 간주할 수 있습니다. 주어진 R, S^ 2의 단위 방향 d는 von Mises-Fisher 분포를 따릅니다.
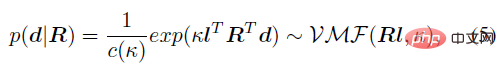
여기서, κ∈R과 d∈S^2는 각각 분포의 집합항과 평균입니다. , l 은 기준 자세(예: T-pose의 단위 뼈 방향은 이론적으로 Rl=d를 만족합니다. 즉, 기준 뼈 방향은 관절 회전을 통해 현재 뼈 방향으로 전달됩니다.
베이지안 이론을 사용하여 사전 분포 p(R) 및 우도 함수 p(d|R)가 주어지면 뼈 방향을 조건으로 하는 관절 회전의 사후 확률 p(R|d)를 계산할 수 있습니다. 분석 형식 의 .
위의 사후 확률은 인간 골격의 방향만을 관찰량으로 고려한 것입니다. 마찬가지로 다른 방향의 관찰량 d_i 또는 회전 관찰량 D_j(IMU와 같은 다른 센서에 의해 생성될 수 있음)로 확장될 수도 있습니다. 등), 다음과 같이 구해집니다. 분석적 사후 확률의 일반적인 형태: 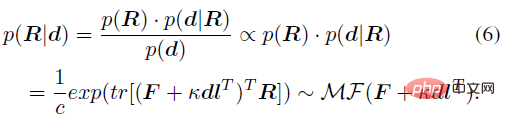
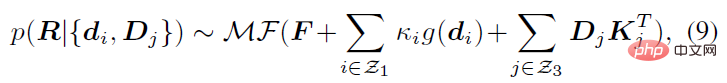
여기서 κ_i와 K_j는 집계 용어입니다. g(⋅)는 방향 관찰을 회전 추정으로 변환할 수 있는 IK 형식의 매핑입니다. g(d_i)=dl^T와 같은 가장 간단한 형식을 취할 수 있습니다. Z_1과 Z_3은 각각 방향 관측 및 회전 관측 세트를 나타냅니다.
특성
이 섹션에서는 사후 확률 분포가 사전 확률 분포보다 집계 수준이 더 높다는 점을 추가로 설명합니다.
앞 섹션에서는 새로운 매개변수 F'를 특징으로 하는 인간 관절 회전의 사후 확률에 대한 분석 형식을 소개했습니다. 사후 매개변수 F^'는 다른 관점에서 이해될 수 있습니다. 즉, F^'는 F와 동일한 평균 항 M과 새로운 집계 항 K^'의 곱입니다.
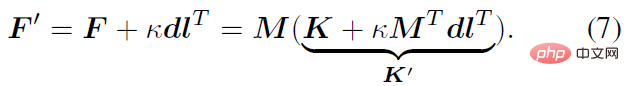
여기서 M^T dl^ T=ll^T 는 랭크 1 실수대칭행렬이고, K 도 실수대칭행렬, 즉 사후집합항 K' 도 실수대칭행렬이다. 행렬해석에서 실수대칭행렬에 대한 시차정리(staggered theorem)에 따르면 K'의 고유값 λ_i'와 K의 고유값 λ_i는 다음과 같은 부등식 관계를 갖는다는 것을 얻을 수 있다.
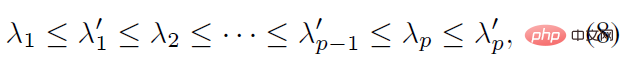
집계항의 고유값은 분포와 동일합니다. 매개변수의 특이값은 분포의 신뢰도를 반영할 수 있습니다. 따라서 우도항이 0이 아닌 경우 사후 추정치가 더 크다는 결론을 내릴 수 있습니다. 이전 추정치보다 집중되어 우도 함수 선호 모드로 빠르게 수렴할 수 있으므로 더 쉽게 학습할 수 있습니다.
선험적 확률법 외에 또 다른 주요 벤치마킹 방법은 역운동학(IK)을 사용하여 뼈 방향을 통해 직접 회전을 계산하는 것입니다. 다음 그림은 사후 확률법과 결정론적 방법의 차이를 직관적으로 보여줍니다. IK 방법 사이의 대비.
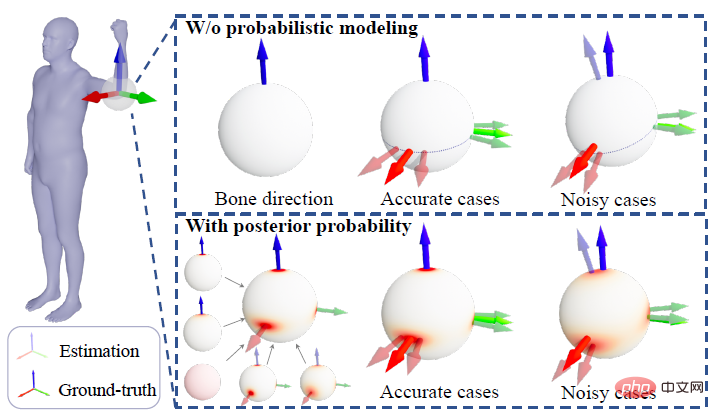
위 사진은 사람의 팔꿈치 관절을 예로 든 것입니다. 실제 3차원 좌표축은 실제 값을 나타내고, 투명한 3차원 좌표축은 추정값을 나타냅니다. 첫 번째 선은 결정론적 IK 방법을 나타냅니다. 이 유형의 모델링 방법은 뼈 방향을 나타내는 벡터입니다. 뼈 방향이 정확하게 추정되면 나머지 1 자유도(비틀림)는 원으로 축소될 수 있습니다. 그림 공의 점선 원) 뼈 방향이 부정확하게 추정되면 가능한 모든 추정치가 실제 값에서 벗어나게 됩니다. 두 번째 선은 다양한 유형의 모델을 융합한 본 연구의 사후 확률 모델을 나타냅니다. 구의 빨간색 영역은 뼈 방향 추정에 오류가 있더라도 특정 회전의 확률을 나타냅니다. , 이 방법은 선험적 또는 기타 관찰을 통해 뼈 방향의 노이즈를 최대한 완화할 수 있기 때문에 이를 실제 값으로 되돌릴 수 있습니다.
네트워크 프레임워크 다이어그램 및 손실 함수
앞서 설명한 이론과 도출을 바탕으로 아래 그림과 같은 프레임워크 다이어그램을 직접 구성할 수 있습니다. 다중 분기 네트워크는 단일 이미지에서 사전 분포 매개변수 F, 3차원 키 포인트 J(뼈 방향 d가 계산되는 기준) 및 모양 매개변수 β를 추정하는 데 사용됩니다. Bayes' rule을 통해 사후 확률을 계산하고, 최종적으로 사후 분포로부터 자세 추정을 구하여 휴먼 메쉬를 출력할 수 있다.
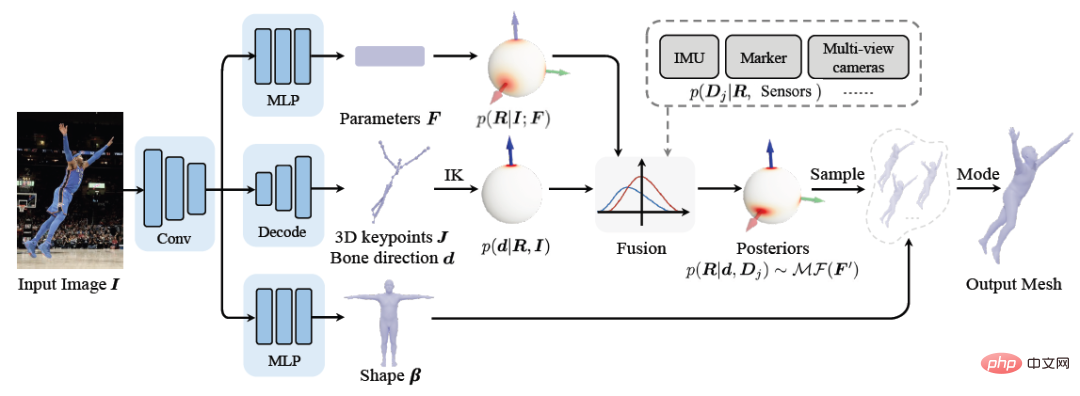
손실 함수의 선택은 비교적 간단하며 다음 네 가지 제약 조건의 가중 합입니다. 여기서 L_J는 키 포인트 제약 조건을 나타내고, L_β는 모양 매개 변수 제약 조건을 나타내고, L_θ는 행렬의 자세 매개 변수 제약 조건을 나타냅니다. form이고 L_s는 샘플링 후 포즈 제약 조건의 분포를 나타냅니다. 분포에 대한 제약과 관련하여 정규화 매개변수의 수치적 안정성이 고려되므로 여기서는 MAP를 직접 사용하지 않습니다. 샘플링 전략에 관해서는 이전 작업과 유사하게 행렬 Fisher 분포를 쿼터니언 형식의 등가 Bingham 분포로 변환한 다음 거부 샘플링을 통해 얻습니다. 여기서 거부 샘플링에 권장되는 분포는 각도 중심 가우스 분포를 채택합니다.
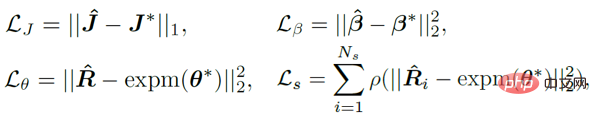
실험 결과
실험 부분에서는 Human3.6M, 3DPW, AGORA, TotalCapture의 공개 데이터 세트를 대상으로 기존 방법과 정량적 비교를 진행했습니다. 본 연구의 방법은 이전의 많은 방법을 능가한다는 것을 알 수 있다. 오른쪽 아래 표의 마지막 회색 행 두 개는 같은 시기의 작품으로, 목록의 완성도를 높이기 위해 여기에 나열합니다.
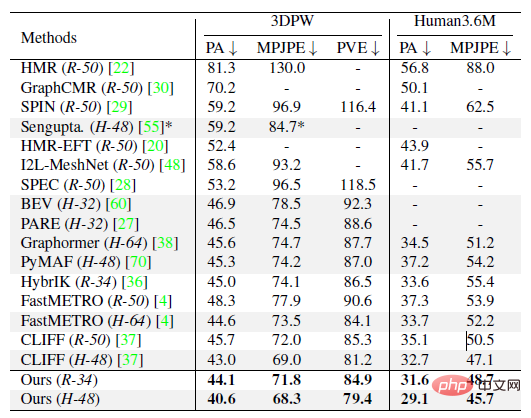
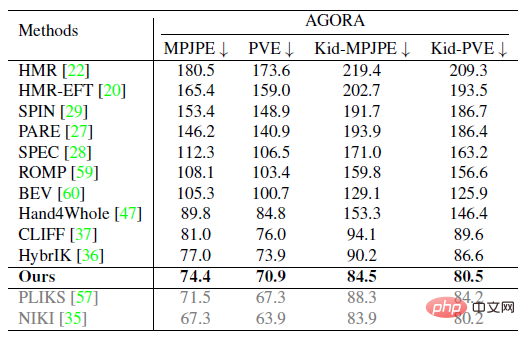
다음 그림은 기존 SOTA 방법인 HybrIK, PARE, CLIFF와 질적 비교를 보여줍니다. 일부 교합 상황에서는 ProPose가 더 나은 결과를 얻을 수 있음을 알 수 있습니다.

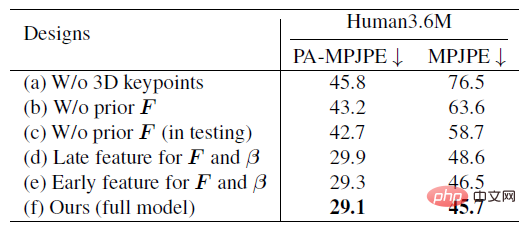
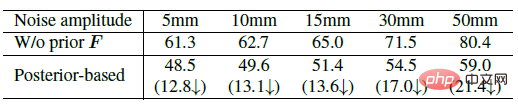
아래 표는 ProPose의 정확성과 견고성을 주로 보여주는 일련의 절제 실험을 보여줍니다. 벤치마크 방법에는 3차원 키 포인트를 사용하지 않음, 사전 확률을 사용하지 않음, 테스트 중 사전 확률을 사용하지 않음, 백본 네트워크의 다른 위치에서 특징을 선택하는 등이 포함됩니다. 아래 왼쪽 표는 제안된 사후 확률 분포가 더 높다는 것을 완전히 검증합니다. 정확성. 아래 오른쪽 표는 사후 방법과 결정론적 IK 방법의 노이즈에 대한 견고성을 비교한 것입니다. 사후 방법이 노이즈 간섭에 더 큰 저항력을 갖고 있음을 알 수 있습니다.
본 연구에서는 위의 HMR 작업 외에도 다중 센서 융합 작업도 평가했습니다. 단일 뷰 및 IMUs 융합의 효과는 다음과 같습니다.
위 내용은 애니메이션 제작 효율이 80% UP! 이 AI 소프트웨어는 원클릭으로 고정밀 비디오 모션 캡처를 실현합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7448
7448
 15
15
 1374
1374
 52
52
 76
76
 11
11
 40
40
 19
19
 14
14
 6
6
 vue.js의 객체로 문자열을 변환하는 데 어떤 방법이 사용됩니까?
Apr 07, 2025 pm 09:39 PM
vue.js의 객체로 문자열을 변환하는 데 어떤 방법이 사용됩니까?
Apr 07, 2025 pm 09:39 PM
표준 JSON 문자열의 경우 vue.js의 객체로 문자열을 변환 할 때 JSON.PARSE ()가 선호됩니다. 비표준 JSON 문자열의 경우, 정규 표현식을 사용하여 문자열을 처리하고 형식 또는 디코딩 된 URL 인코딩에 따라 방법을 줄일 수 있습니다. 문자열 형식에 따라 적절한 방법을 선택하고 버그를 피하기 위해 보안 및 인코딩 문제에주의를 기울이십시오.
 vue.js 문자열 유형 배열을 객체 배열로 변환하는 방법은 무엇입니까?
Apr 07, 2025 pm 09:36 PM
vue.js 문자열 유형 배열을 객체 배열로 변환하는 방법은 무엇입니까?
Apr 07, 2025 pm 09:36 PM
요약 : vue.js 문자열 배열을 객체 배열로 변환하는 다음 방법이 있습니다. 기본 메소드 : 정기적 인 형식의 데이터에 맞게 맵 함수를 사용하십시오. 고급 게임 플레이 : 정규 표현식을 사용하면 복잡한 형식을 처리 할 수 있지만 신중하게 작성하고 고려해야합니다. 성능 최적화 : 많은 양의 데이터를 고려하면 비동기 작업 또는 효율적인 데이터 처리 라이브러리를 사용할 수 있습니다. 모범 사례 : 명확한 코드 스타일, 의미있는 변수 이름과 주석을 사용하여 코드를 간결하게 유지하십시오.
 Vue Axios의 시간 초과를 설정하는 방법
Apr 07, 2025 pm 10:03 PM
Vue Axios의 시간 초과를 설정하는 방법
Apr 07, 2025 pm 10:03 PM
vue axios의 타임 아웃을 설정하려면 axios 인스턴스를 생성하고 시간 초과 옵션을 지정할 수 있습니다. 글로벌 설정에서 : vue.prototype. $ axios = axios.create ({timeout : 5000}); 단일 요청 : this. $ axios.get ( '/api/user', {timeout : 100000}).
 Laravel 's geospatial : 대화식지도의 최적화 및 많은 양의 데이터
Apr 08, 2025 pm 12:24 PM
Laravel 's geospatial : 대화식지도의 최적화 및 많은 양의 데이터
Apr 08, 2025 pm 12:24 PM
7 백만 레코드를 효율적으로 처리하고 지리 공간 기술로 대화식지도를 만듭니다. 이 기사는 Laravel과 MySQL을 사용하여 7 백만 개 이상의 레코드를 효율적으로 처리하고 대화식지도 시각화로 변환하는 방법을 살펴 봅니다. 초기 챌린지 프로젝트 요구 사항 : MySQL 데이터베이스에서 7 백만 레코드를 사용하여 귀중한 통찰력을 추출합니다. 많은 사람들이 먼저 프로그래밍 언어를 고려하지만 데이터베이스 자체를 무시합니다. 요구 사항을 충족시킬 수 있습니까? 데이터 마이그레이션 또는 구조 조정이 필요합니까? MySQL이 큰 데이터로드를 견딜 수 있습니까? 예비 분석 : 주요 필터 및 속성을 식별해야합니다. 분석 후, 몇 가지 속성만이 솔루션과 관련이 있음이 밝혀졌습니다. 필터의 타당성을 확인하고 검색을 최적화하기위한 제한 사항을 설정했습니다. 도시를 기반으로 한지도 검색
 원격 선임 백엔드 엔지니어 (플랫폼)에는 원이 필요합니다
Apr 08, 2025 pm 12:27 PM
원격 선임 백엔드 엔지니어 (플랫폼)에는 원이 필요합니다
Apr 08, 2025 pm 12:27 PM
원격 선임 백엔드 엔지니어 구직 회사 : 원 위치 : 원격 사무실 직무 유형 : 전임 급여 : $ 130,000- $ 140,000 직무 설명 전체 소프트웨어 개발 라이프 사이클을 다루는 Circle Mobile 애플리케이션 및 공개 API 관련 기능의 연구 및 개발에 참여합니다. 주요 책임은 독립적으로 Rubyonrails를 기반으로 개발 작업을 완료하고 React/Redux/Relay 프론트 엔드 팀과 협력합니다. 웹 애플리케이션의 핵심 기능 및 개선을 구축하고 기능 설계 프로세스 전반에 걸쳐 설계자 및 리더십과 긴밀히 협력하십시오. 긍정적 인 개발 프로세스를 촉진하고 반복 속도를 우선시하십시오. 6 년 이상의 복잡한 웹 애플리케이션 백엔드가 필요합니다.
 MySQL을 해결하는 방법을 시작할 수 없습니다
Apr 08, 2025 pm 02:21 PM
MySQL을 해결하는 방법을 시작할 수 없습니다
Apr 08, 2025 pm 02:21 PM
MySQL 시작이 실패하는 데는 여러 가지 이유가 있으며 오류 로그를 확인하여 진단 할 수 있습니다. 일반적인 원인에는 포트 충돌 (포트 점유 체크 및 구성 수정), 권한 문제 (서비스 실행 사용자 권한 실행), 구성 파일 오류 (파라미터 설정 확인), 데이터 디렉토리 손상 (데이터 복원 또는 테이블 공간 재건), IBDATA 테이블 공간 문제 (IBDATA1 파일 확인), 플러그로드 (확인 오류 로그)가 포함됩니다. 문제를 해결할 때 오류 로그를 기반으로 문제를 분석하고 문제의 근본 원인을 찾고 문제를 방지하고 해결하기 위해 정기적으로 데이터를 백업하는 습관을 개발해야합니다.
 설치 후 MySQL을 사용하는 방법
Apr 08, 2025 am 11:48 AM
설치 후 MySQL을 사용하는 방법
Apr 08, 2025 am 11:48 AM
이 기사는 MySQL 데이터베이스의 작동을 소개합니다. 먼저 MySQLworkBench 또는 명령 줄 클라이언트와 같은 MySQL 클라이언트를 설치해야합니다. 1. MySQL-Uroot-P 명령을 사용하여 서버에 연결하고 루트 계정 암호로 로그인하십시오. 2. CreateABase를 사용하여 데이터베이스를 작성하고 데이터베이스를 선택하십시오. 3. CreateTable을 사용하여 테이블을 만들고 필드 및 데이터 유형을 정의하십시오. 4. InsertInto를 사용하여 데이터를 삽입하고 데이터를 쿼리하고 업데이트를 통해 데이터를 업데이트하고 DELETE를 통해 데이터를 삭제하십시오. 이러한 단계를 마스터하고 일반적인 문제를 처리하는 법을 배우고 데이터베이스 성능을 최적화하면 MySQL을 효율적으로 사용할 수 있습니다.
 MySQL 설치 후 데이터베이스 성능을 최적화하는 방법
Apr 08, 2025 am 11:36 AM
MySQL 설치 후 데이터베이스 성능을 최적화하는 방법
Apr 08, 2025 am 11:36 AM
MySQL 성능 최적화는 설치 구성, 인덱싱 및 쿼리 최적화, 모니터링 및 튜닝의 세 가지 측면에서 시작해야합니다. 1. 설치 후 innodb_buffer_pool_size 매개 변수와 같은 서버 구성에 따라 my.cnf 파일을 조정해야합니다. 2. 과도한 인덱스를 피하기 위해 적절한 색인을 작성하고 Execution 명령을 사용하여 실행 계획을 분석하는 것과 같은 쿼리 문을 최적화합니다. 3. MySQL의 자체 모니터링 도구 (showprocesslist, showstatus)를 사용하여 데이터베이스 건강을 모니터링하고 정기적으로 백업 및 데이터베이스를 구성하십시오. 이러한 단계를 지속적으로 최적화함으로써 MySQL 데이터베이스의 성능을 향상시킬 수 있습니다.




