머신러닝 기반의 수치적 거리: 공간 내 점 사이의 거리

이 글은 위챗 공개 계정 '정보화 시대에 살기'에서 재인쇄되었습니다. 이 기사를 재인쇄하려면 Living in the Information Age 공개 계정에 문의하세요.

머신러닝에서는 두 샘플 간의 유사성과 카테고리 정보를 평가할 수 있도록 두 샘플의 차이를 판단하는 방법이 기본 개념입니다. 이러한 유사성을 판단하는 척도는 특징 공간에서 두 샘플 사이의 거리입니다.

다양한 데이터 특성에 따라 다양한 측정 방법이 있습니다. 일반적으로 두 데이터 샘플 x, y에 대해 함수 d(x, y)를 정의합니다. 두 샘플 사이의 거리로 정의되면 d(x, y)는 다음 기본 속성을 충족해야 합니다.

비음수: d(x,y)>=0

• 동일성: d(x,y)=0 ⇔ x=y
• 대칭: d(x,y)=d(y, x)
• 삼각형 불평등: d(x, y)
• 일반적으로 일반적인 거리 측정에는 다음이 포함됩니다: 공간 내 점의 거리, 문자열 거리에는 네 가지 유형이 있습니다. 세트, 변수/개념 분포 사이의 거리.

오늘은 먼저 우주에서 가장 흔히 사용되는 점의 거리를 소개하겠습니다.

공간 내 점 사이의 거리는 다음과 같은 유형이 있습니다.

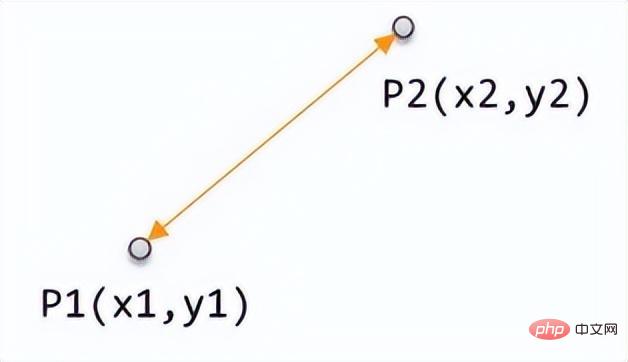
1. 유클리드 거리

두 점 사이의 거리가 사람들에게 가장 친숙한 거리임은 의심의 여지가 없습니다. 사이의 거리. 중학교 수학을 공부한 학생들은 모두 2차원 공간에서 데카르트 좌표계의 두 점 사이의 거리를 계산하는 방법을 알고 있습니다. 계산 공식은 다음과 같습니다.

N차원 공간으로 확장된 유클리드. distance is :

2. Manhattan Distance

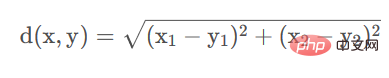
Manhattan Distance는 택시 거리라고도 불리며, 수평 및 수직 블록이 많은 뉴욕 맨해튼에서 유래되었습니다. 택시 운전사가 한 지점에서 다른 지점으로 걸어가려고 할 때 직선 거리를 계산하는 것은 쓸모가 없습니다. 택시가 건물 위로 날아갈 수 없기 때문입니다. 따라서 이 거리는 일반적으로 두 지점의 동서 거리와 남북 거리를 각각 빼고 더하여 계산됩니다. 이것이 택시가 실제로 이동해야 하는 거리입니다.

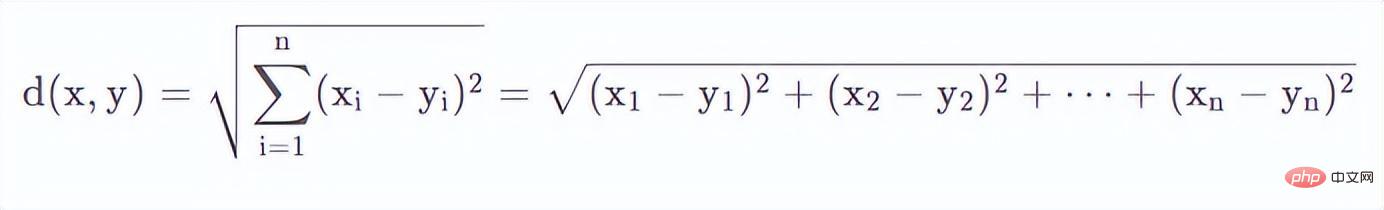
사진에 표시된 것처럼 빨간색 선과 노란색 선은 서로 다른 두 경로의 맨해튼 거리입니다. 수학적으로 2차원 공간에서 맨해튼 거리를 계산하는 방법은 다음과 같습니다.

3. 체비쇼프 거리(Chebyshev Distance)

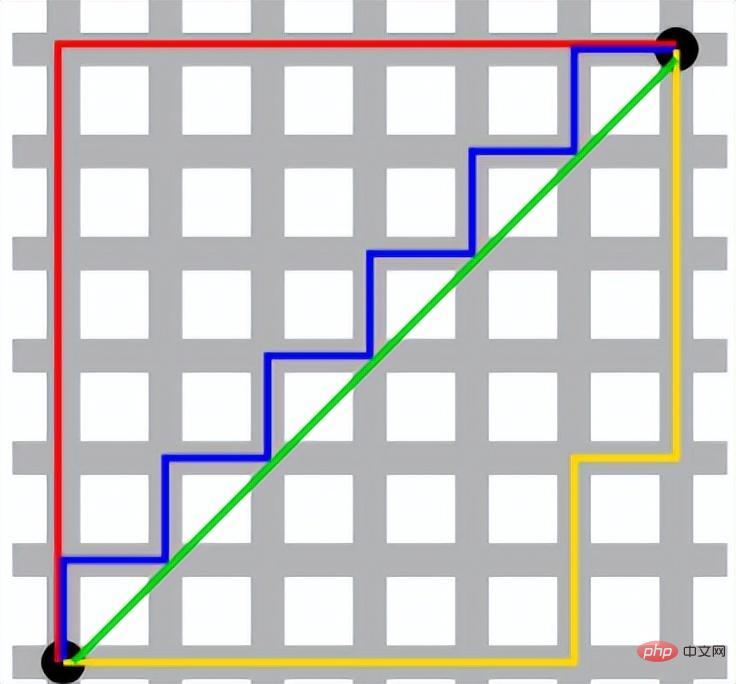
체비셰프 거리는 두 점 사이의 각 좌표의 수치 차이로 정의됩니다. .최대값.

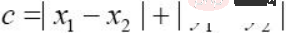
가장 직관적인 예는 체스의 왕입니다. 왜냐하면 옆으로, 직선으로, 대각선으로 움직일 수 있지만 한 번에 한 칸만 움직일 수 있기 때문에 체비쇼프 거리는 그가 다른 칸으로 이동해야 할 때입니다. 그리드에 필요한 최소 거리.

4. 민코프스키 거리

민코프스키 거리 자체는 특별한 거리가 아니고, 여러 거리(맨해튼 거리, 유클리드 거리, 체비셰프 거리)의 조합을 하나의 공식으로 합친 것입니다.

두 개의 n차원 변수에 대해 Min의 거리는 다음과 같이 정의됩니다.

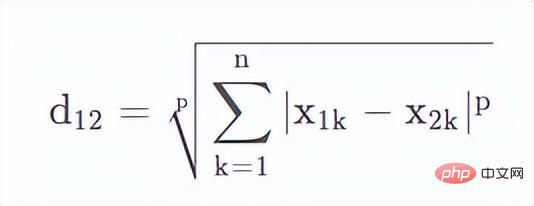
p=1이면

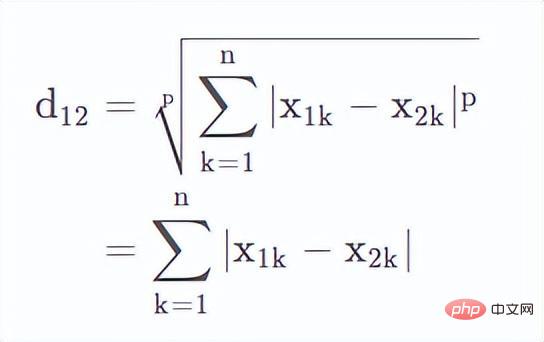
이 현재 맨해튼 거리임을 알 수 있습니다.

p=2일 때

이 이때의 유클리드 거리임을 알 수 있습니다.

p=π일 때

이 체비쇼프 거리임을 알 수 있습니다.

5. 표준화된 유클리드 거리

유클리드 거리는 두 점 사이의 직선 거리를 측정할 수 있지만 경우에 따라 다른 단위의 영향을 받을 수도 있습니다. 예를 들어, 동시에 5mm의 키 차이와 5kg의 체중 차이가 있다면, 인식은 전혀 다를 수 있습니다. 세 가지 모델을 클러스터링하려는 경우 해당 속성은 다음과 같습니다.

A: 65000000mg(예: 65kg), 1.74m

B: 60000000mg(예: 60kg), 1.70m

C: 65000000mg( 즉, 65kg), 1.40미터

우리가 일반적으로 이해하는 바에 따르면 A와 B는 더 나은 수치를 지닌 모델이므로 동일한 카테고리로 분류되어야 합니다. 그러나 실제로 위의 단위로 계산해 보면 A와 B의 차이보다 A와 C의 차이가 더 큰 것을 알 수 있다. 그 이유는 속성의 서로 다른 측정 단위로 인해 과도한 수치 차이가 발생하기 때문입니다. 동일한 데이터가 다른 장치로 변경된 경우.

A: 65kg, 174cm

B: 60kg, 170cm

C: 65kg, 140cm

그러면 우리가 생각한 결과인 A와 B를 같은 카테고리로 분류하게 됩니다. 따라서 측정 단위의 차이로 인한 이러한 차이를 방지하기 위해 표준화된 유클리드 거리를 도입해야 합니다. 이 거리 계산에서 각 구성 요소는 평균과 분산이 동일한 구간으로 정규화됩니다.

샘플 세트 X의 평균(평균)이 m이고 표준 편차(표준 편차)가 s라고 가정하면 값의 "표준화 변수" - 구성 요소의 평균) / 표준 편차 요소. 간단한 유도 후에 두 n차원 벡터 간의 표준화된 유클리드 거리 공식을 얻을 수 있습니다.

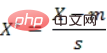
분산의 역수를 가중치로 간주하면 이 공식은 가중 유클리드 거리(Weighted Euclidean Distance)로 간주될 수 있습니다. 유클리드 거리). 이 작업을 통해 서로 다른 중량 단위 간의 차이를 효과적으로 제거합니다.

6. 랜스 거리(Lance and Williams Distance)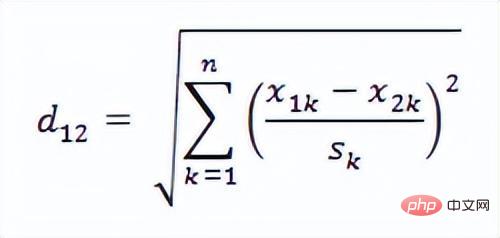

랜스 거리(Lance distance)는 캔버라 거리(Canberra distance)라고도 불리며,

민의 거리와 다양한 지표의 차이를 극복한 무차원 지표입니다. 큰 특이값에 민감하지 않으므로 스케줄링 편향이 있는 데이터에 특히 적합합니다. 그러나 이 거리는 변수 간의 상관관계도 고려하지 않습니다. 따라서 변수 간의 상관관계를 고려해야 한다면 여전히 Mahalanobis 거리가 필요합니다.

7. 마할라노비스 거리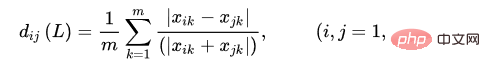

값을 정규화하면 문제가 없나요? 아마도. 예를 들어 1차원 예에서 두 개의 클래스가 있는 경우 한 클래스의 평균은 0, 분산은 0.1이고 다른 클래스의 평균은 5, 분산 5입니다. 그렇다면 값이 2인 점이 어느 카테고리에 속해야 할까요? 우리는 그것이 두 번째 범주임에 틀림없다고 직관적으로 생각합니다. 왜냐하면 첫 번째 범주는 분명히 수치적으로 2에 도달할 가능성이 없기 때문입니다. 그러나 실제로 거리를 두고 계산하면 숫자 2가 첫 번째 범주에 속해야 합니다.

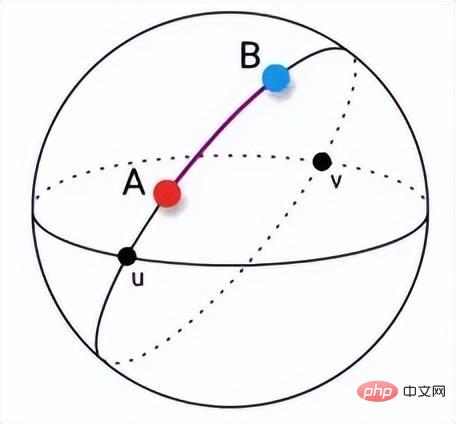
따라서 작은 차이가 있는 차원에서는 작은 차이도 이상값이 될 수 있습니다. 예를 들어, 아래 그림에서 A와 B는 원점으로부터 같은 거리에 있지만 전체 표본이 가로축을 따라 분포되어 있기 때문에 B점은 표본 내의 한 점이 될 가능성이 높고 A점은 더 가깝습니다. 이상치일 가능성이 높습니다.

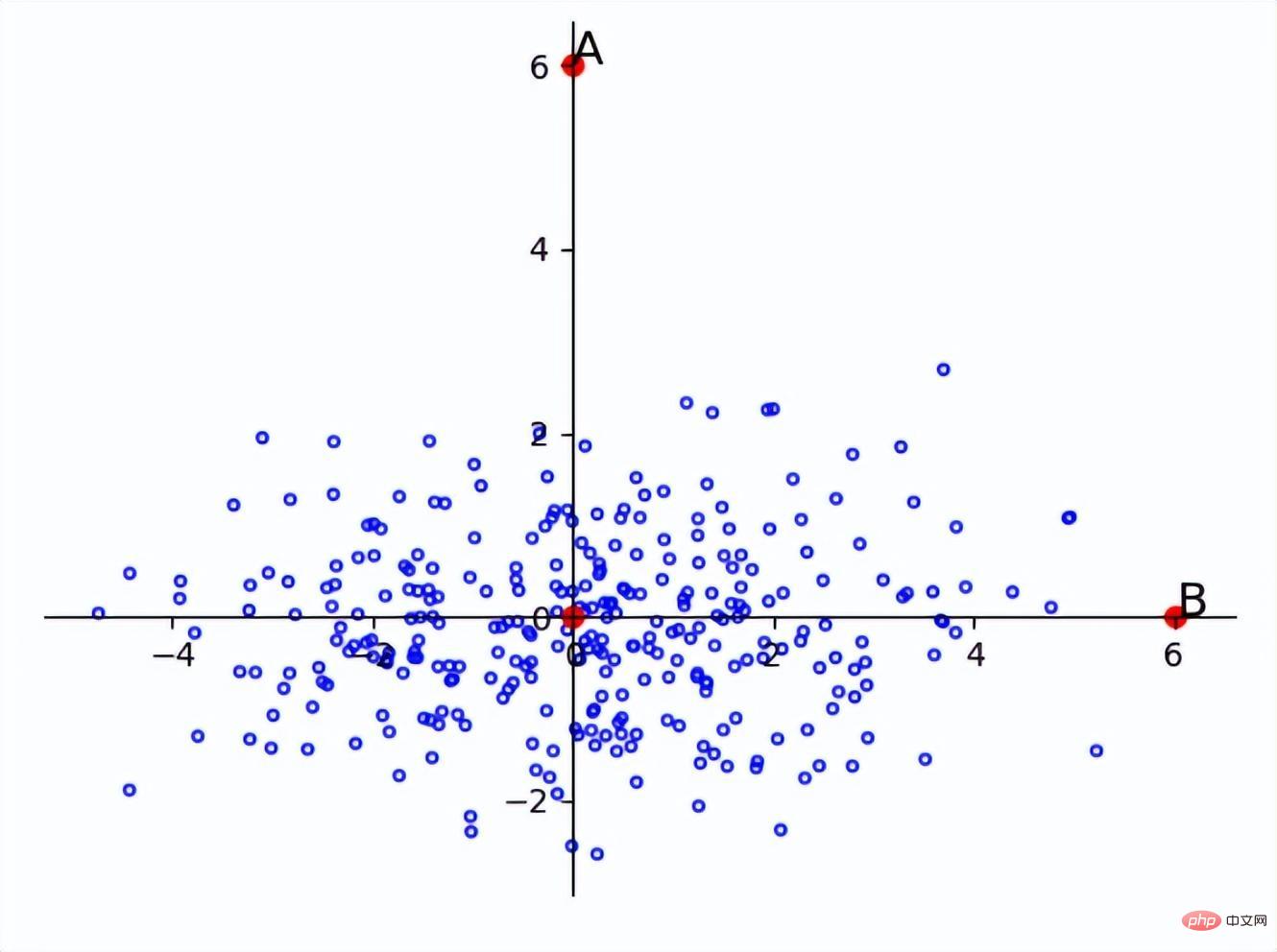
차원이 독립적이지 않고 동일하게 분포된 경우에도 문제가 발생합니다. 예를 들어 아래 그림에서 점 A와 점 B는 원점으로부터의 거리와 같지만 주요 분포는 유사합니다. f(x) =x이므로 A는 이상치에 더 가깝습니다.

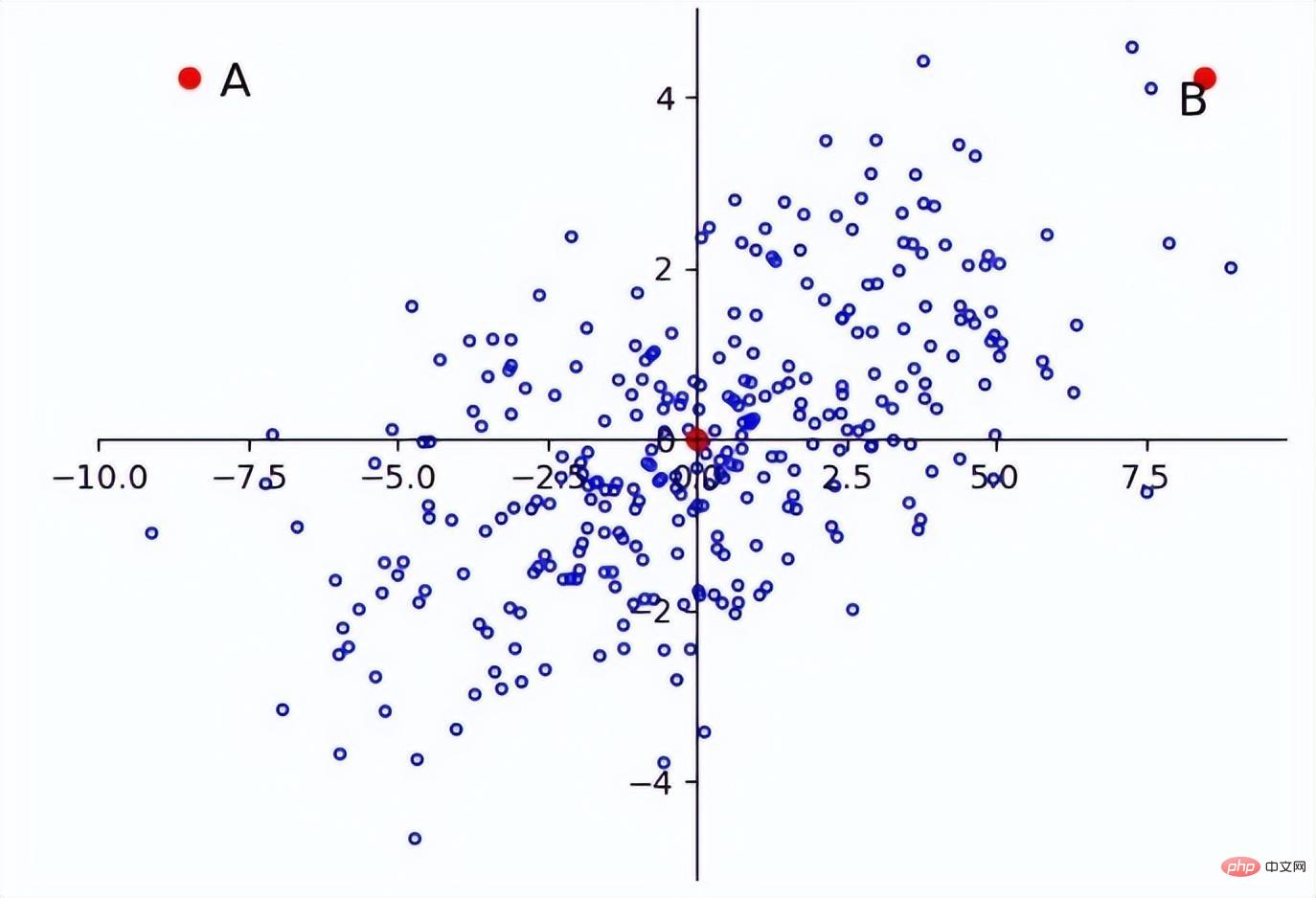
이 경우 표준화된 유클리드 거리에도 문제가 있으므로 마할라노비스 거리를 도입해야 함을 알 수 있습니다.

마할라노비스 거리는 주성분에 따라 변수를 회전시켜 차원을 서로 독립적으로 만든 다음 표준화하여 차원을 균등하게 분포시킵니다. 주성분은 고유벡터의 방향이므로 고유벡터의 방향에 따라 회전한 다음 고유값 시간을 조정하면 됩니다. 예를 들어 위 이미지를 변환하면 다음과 같은 결과를 얻게 됩니다.

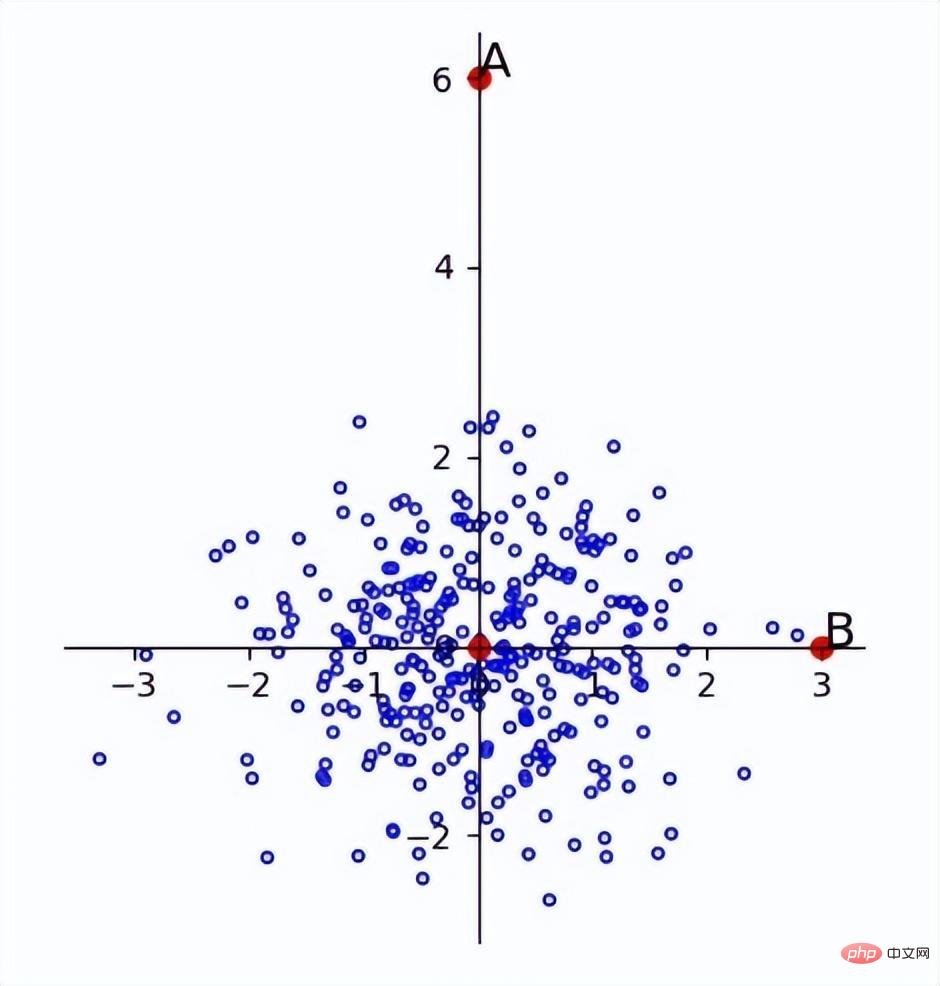
이상값이 성공적으로 분리된 것을 확인할 수 있습니다.

마할라노비스 거리는 인도 수학자 마할라노비스가 제안한 것으로 데이터의 공분산 거리를 나타냅니다. 두 개의 알려지지 않은 샘플 세트의 유사성을 계산하는 효율적인 방법입니다.

평균

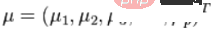
및 공분산 행렬 Σ를 갖는 다변량 벡터

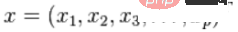
의 경우 Mahalanobis 거리(단일 데이터 포인트의 Mahalanobis 거리)는 다음과 같습니다.

For 동일한 분포를 따르고 공분산 행렬이 Σ인 두 확률 변수 X와 Y 간의 차이 정도, 데이터 점 x, y 사이의 Mahalanobis 거리는 다음과 같습니다.

공분산 행렬이 항등 행렬을 사용하면 Mahalanobis 거리가 유클리드 거리로 단순화됩니다. 공분산 행렬이 대각 행렬인 경우 Mahalanobis 거리는 표준화된 유클리드 거리가 됩니다.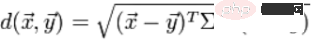

8. 코사인 거리(Cosine Distance)

이름에서 알 수 있듯이 코사인 거리는 거리나 길이가 아닌 두 벡터의 방향 차이를 측정하는 데 사용할 수 있습니다. 코사인 값이 0이면 두 벡터는 직교하고 끼인각은 90도입니다. 각도가 작을수록 코사인 값이 1에 가까워지고 방향이 더 일관됩니다. N차원 공간에서 코사인 거리는 다음과 같습니다.

코사인 거리는 삼각형 부등식을 만족하지 않는다는 점을 지적할 가치가 있습니다.

9. 측지선 거리

측지선 거리는 원래 구 표면 사이의 최단 거리를 의미합니다. 특징 공간이 평면인 경우 측지선 거리는 유클리드 거리입니다. 비유클리드 기하학에서 구의 두 점 사이의 가장 짧은 선은 두 점을 연결하는 큰 호입니다. 구의 삼각형과 다각형의 측면도 이러한 큰 호로 구성됩니다.

10. Bray Curtis 거리

Bray Curtis 거리는 식물학, 생태학, 환경 과학에서 주로 사용되며, 표본 간의 차이를 계산하는 데 사용될 수 있습니다. 공식은 다음과 같습니다.

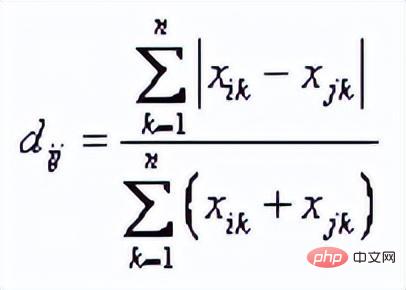
값은 [0, 1] 사이에 있습니다. 두 벡터 좌표가 모두 0이면 값은 의미가 없습니다.

위 내용은 머신러닝 기반의 수치적 거리: 공간 내 점 사이의 거리의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!