11가지 일반적인 분류 특징 인코딩 기술

기계 학습 알고리즘은 숫자 입력만 허용하므로 범주형 특성을 발견하면 범주형 특성을 인코딩합니다. 이 문서에서는 11가지 일반적인 범주형 변수 인코딩 방법을 요약합니다.

1. ONE HOT ENCODING

가장 널리 사용되고 일반적으로 사용되는 인코딩 방법은 One Hot Enoding입니다. n개의 관측값과 d개의 개별 값을 갖는 단일 변수는 n개의 관측값을 갖는 d개의 이진 변수로 변환되며, 각 이진 변수는 비트(0, 1)로 식별됩니다.

예:

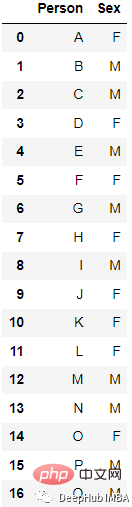
인코딩 후

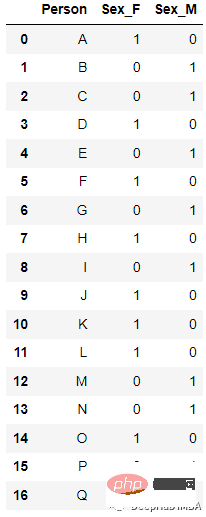
가장 간단한 구현은 pandas의 get_dummies

new_df=pd.get_dummies(columns=[‘Sex’], data=df)

2, 라벨 인코딩을 사용하는 것입니다.

고유하게 식별되는 정수를 범주형 데이터 변수에 할당합니다. 이 방법은 매우 간단하지만 순서가 지정되지 않은 데이터를 나타내는 범주형 변수에 문제를 일으킬 수 있습니다. 예를 들어, 값이 높은 태그는 값이 낮은 태그보다 우선순위가 더 높을 수 있습니다.

예를 들어 위 데이터에서 인코딩 후 다음과 같은 결과를 얻었습니다.

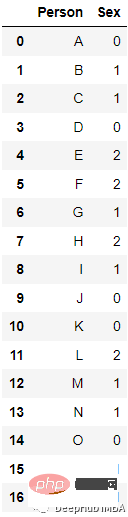
sklearn의 LabelEncoder는 직접 변환할 수 있습니다.

from sklearn.preprocessing import LabelEncoder
 le=LabelEncoder()
 df[‘Sex’]=le.fit_transform(df[‘Sex’])

3. Label Binarizer

LabelBinarizer는 다음에서 레이블 매트릭스를 생성하는 데 사용되는 도구입니다. 다중 카테고리 목록 목록을 입력 세트의 고유 값과 정확히 동일한 수의 열을 갖는 행렬로 변환하는 유틸리티 클래스입니다.

예를 들어, 이 데이터는

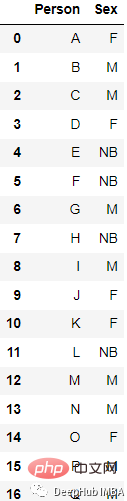
변환된 결과는

from sklearn.preprocessing import LabelBinarizer
 lb = LabelBinarizer()
 new_df[‘Sex’]=lb.fit_transform(df[‘Sex’])

4입니다. 인코딩을 하나만 남겨두면 대상 범주형 특성 변수에 대해 동일한 값을 갖는 모든 레코드가 됩니다. 평균을 구하여 목표 변수의 평균을 결정합니다. 인코딩 알고리즘은 훈련 데이터세트와 테스트 데이터세트 간에 약간 다릅니다. 분류 대상으로 고려되는 특징 레코드는 훈련 데이터 세트에서 제외되기 때문에 "Leave One Out"이라고 합니다.

특정 범주형 변수의 구체적인 값을 코딩하는 방법은 다음과 같습니다.

ci = (Σj != i tj / (n — 1 + R)) x (1 + εi) where
 ci = encoded value for ith record
 tj = target variable value for jth record
 n = number of records with the same categorical variable value
 R = regularization factor
 εi = zero mean random variable with normal distribution N(0, s)

예를 들어 다음 데이터는 다음과 같습니다.

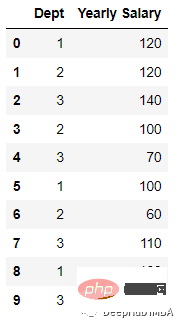인코딩 후:

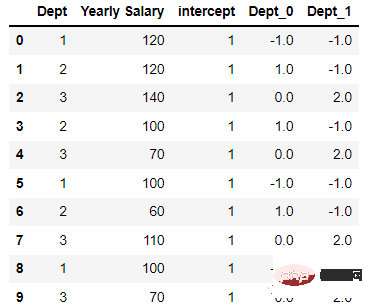
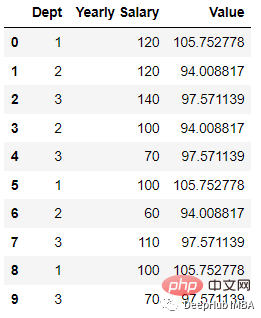이 인코딩 프로세스를 보여주기 위해 데이터 세트

import pandas as pd;
 data = [[‘1’, 120], [‘2’, 120], [‘3’, 140],
 [‘2’, 100], [‘3’, 70], [‘1’, 100],[‘2’, 60],
 [‘3’, 110], [‘1’, 100],[‘3’, 70] ]
 df = pd.DataFrame(data, columns = [‘Dept’,’Yearly Salary’])

를 만든 다음 이를 인코딩합니다.

import category_encoders as ce
 tenc=ce.TargetEncoder()
 df_dep=tenc.fit_transform(df[‘Dept’],df[‘Yearly Salary’])
 df_dep=df_dep.rename({‘Dept’:’Value’}, axis=1)
 df_new = df.join(df_dep)

이 방법으로 우리는 다음을 얻습니다. 위의 결과.

5. 해싱

해시 함수를 사용하면 문자열이 고유한 해시 값으로 변환됩니다. 메모리를 거의 사용하지 않고 더 많은 범주형 데이터를 처리할 수 있기 때문입니다. 기능 해싱은 기계 학습에서 희박한 고차원 기능을 관리하는 효과적인 방법입니다. 온라인 학습 시나리오에 적합하며 빠르고 간단하며 효율적이고 빠른 특성을 가지고 있습니다.

예를 들어 다음 데이터는

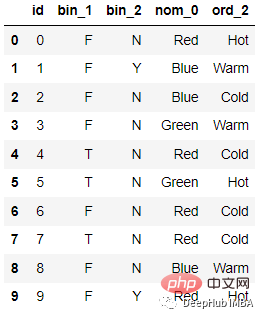인코딩 후

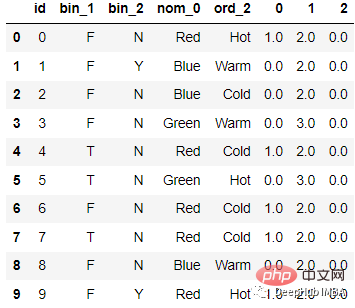코드는 다음과 같습니다.

from sklearn.feature_extraction import FeatureHasher
 # n_features contains the number of bits you want in your hash value.
 h = FeatureHasher(n_features = 3, input_type =’string’)
 # transforming the column after fitting
 hashed_Feature = h.fit_transform(df[‘nom_0’])
 hashed_Feature = hashed_Feature.toarray()
 df = pd.concat([df, pd.DataFrame(hashed_Feature)], axis = 1)
 df.head(10)

6. Weight of Evidence Encoding

(WoE) 개발의 주요 목표는 금융 산업의 신용 및 대출 불이행 위험을 평가하기 위한 예측 모델. 증거가 이론을 지지하거나 반박하는 정도는 증거의 가중치(WOE)에 따라 달라집니다.

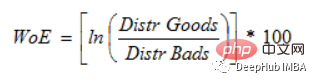P(Goods) / P(Bads) = 1이면 WoE는 0입니다. 이 그룹의 결과가 무작위인 경우 P(나쁨) > P(좋음)이면 승산비는 1이고 증거의 가중치(WoE)는 0입니다. 그룹에서 P(Goods) > P(bad)인 경우 WoE는 0보다 큽니다.

因为Logit转换只是概率的对数，或ln(P(Goods)/P(bad))，所以WoE非常适合于逻辑回归。当在逻辑回归中使用wo编码的预测因子时，预测因子被处理成与编码到相同的尺度，这样可以直接比较线性逻辑回归方程中的变量。

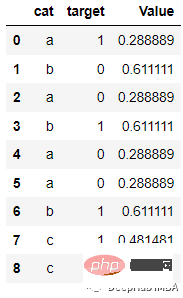
例如下面的数据

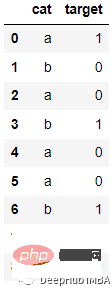
会被编码为：

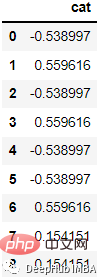
代码如下：

from category_encoders import WOEEncoder
 df = pd.DataFrame({‘cat’: [‘a’, ‘b’, ‘a’, ‘b’, ‘a’, ‘a’, ‘b’, ‘c’, ‘c’], ‘target’: [1, 0, 0, 1, 0, 0, 1, 1, 0]})
 woe = WOEEncoder(cols=[‘cat’], random_state=42)
 X = df[‘cat’]
 y = df.target
 encoded_df = woe.fit_transform(X, y)

7、Helmert Encoding

Helmert Encoding将一个级别的因变量的平均值与该编码中所有先前水平的因变量的平均值进行比较。

反向 Helmert 编码是类别编码器中变体的另一个名称。它将因变量的特定水平平均值与其所有先前水平的水平的平均值进行比较。

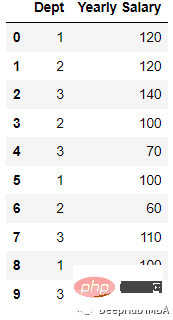
会被编码为

代码如下：

import category_encoders as ce
 encoder=ce.HelmertEncoder(cols=’Dept’)
 new_df=encoder.fit_transform(df[‘Dept’])
 new_hdf=pd.concat([df,new_df], axis=1)
 new_hdf

8、Cat Boost Encoding

是CatBoost编码器试图解决的是目标泄漏问题，除了目标编码外，还使用了一个排序概念。它的工作原理与时间序列数据验证类似。当前特征的目标概率仅从它之前的行(观测值)计算，这意味着目标统计值依赖于观测历史。

TargetCount:某个类别特性的目标值的总和(到当前为止)。

Prior:它的值是恒定的，用(数据集中的观察总数(即行))/(整个数据集中的目标值之和)表示。

featucalculate:到目前为止已经看到的、具有与此相同值的分类特征的总数。

编码后的结果如下：

代码：

import category_encoders
 category_encoders.cat_boost.CatBoostEncoder(verbose=0,
 cols=None, drop_invariant=False, return_df=True,
 handle_unknown=’value’, handle_missing=’value’,
 random_state=None, sigma=None, a=1)
 
 target = df[[‘target’]]
 train = df.drop(‘target’, axis = 1)
 
 # Define catboost encoder
 cbe_encoder = ce.cat_boost.CatBoostEncoder()
 
 # Fit encoder and transform the features
 cbe_encoder.fit(train, target)
 train_cbe = cbe_encoder.transform(train)

9、James Stein Encoding

James-Stein 为特征值提供以下加权平均值：

• 观察到的特征值的平均目标值。
• 平均期望值（与特征值无关）。

James-Stein 编码器将平均值缩小到全局的平均值。该编码器是基于目标的。但是James-Stein 估计器有缺点：它只支持正态分布。

它只能在给定正态分布的情况下定义（实时情况并非如此）。为了防止这种情况，我们可以使用 beta 分布或使用对数-比值比转换二元目标，就像在 WOE 编码器中所做的那样（默认使用它，因为它很简单）。

10、M Estimator Encoding:

Target Encoder的一个更直接的变体是M Estimator Encoding。它只包含一个超参数m，它代表正则化幂。m值越大收缩越强。建议m的取值范围为1 ~ 100。

11、 Sum Encoder

Sum Encoder将类别列的特定级别的因变量(目标)的平均值与目标的总体平均值进行比较。在线性回归(LR)的模型中，Sum Encoder和ONE HOT ENCODING都是常用的方法。两种模型对LR系数的解释是不同的，Sum Encoder模型的截距代表了总体平均值(在所有条件下)，而系数很容易被理解为主要效应。在OHE模型中，截距代表基线条件的平均值，系数代表简单效应(一个特定条件与基线之间的差)。

最后，在编码中我们用到了一个非常好用的Python包 “category-encoders”它还提供了其他的编码方法，如果你对他感兴趣，请查看它的官方文档：

http://contrib.scikit-learn.org/category_encoders/

위 내용은 11가지 일반적인 분류 특징 인코딩 기술의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!