
파트 01
●이미지 임베딩이란 무엇인가요 ●
그래프 임베딩은 그래프 구조의 매핑입니다. 데이터는 저차원 밀집 벡터의 처리이며, 동시에 원본 그래프에서 유사한 토폴로지 구조나 가까운 속성을 가진 노드도 벡터 공간에서 위치가 가깝기 때문에 그래프가 다음과 같은 문제를 잘 해결할 수 있습니다. 구조화된 데이터는 머신러닝 알고리즘에 효율적으로 입력하기 어렵습니다.
그래프의 표현과 저장에 있어서 가장 쉽게 생각할 수 있는 방법은 인접행렬(Adjacency Matrix)을 이용하는 것입니다. 그래프의 각 노드에 번호를 매겨  행렬을 구성합니다. 여기서
행렬을 구성합니다. 여기서 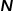 은 그래프의 노드 수를 나타냅니다. 그래프의 두 노드가 간선으로 연결되어 있는지 여부에 따라 인접 행렬의 해당 위치 값이 결정됩니다. 이 표현 방법은 매우 이해하기 쉽고 직관적이지만 매우 비효율적입니다. 실제 시나리오의 그래프에는 수천 개 이상의 노드가 포함될 수 있고 대부분의 노드는 가장자리로 연결되지 않으므로 결과 인접 행렬이 매우 희박해집니다. 그래프를 표현하고 저장하기 위해 인접 행렬을 사용하려면 높은 계산 비용과 공간 비용이 필요한 반면, 그래프 임베딩 알고리즘은 그래프 분석 문제를 효율적으로 해결할 수 있습니다.
은 그래프의 노드 수를 나타냅니다. 그래프의 두 노드가 간선으로 연결되어 있는지 여부에 따라 인접 행렬의 해당 위치 값이 결정됩니다. 이 표현 방법은 매우 이해하기 쉽고 직관적이지만 매우 비효율적입니다. 실제 시나리오의 그래프에는 수천 개 이상의 노드가 포함될 수 있고 대부분의 노드는 가장자리로 연결되지 않으므로 결과 인접 행렬이 매우 희박해집니다. 그래프를 표현하고 저장하기 위해 인접 행렬을 사용하려면 높은 계산 비용과 공간 비용이 필요한 반면, 그래프 임베딩 알고리즘은 그래프 분석 문제를 효율적으로 해결할 수 있습니다.
파트 02
● 기본 개념 ●
콘셉트 1 사진 :
그래프는 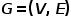 로 표시됩니다. 여기서
로 표시됩니다. 여기서 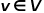 은 노드를 나타내고
은 노드를 나타내고 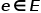 는 가장자리를 나타냅니다.
는 가장자리를 나타냅니다. 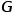 은 노드 유형 매핑 기능
은 노드 유형 매핑 기능 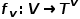 및 가장자리 유형 매핑 기능
및 가장자리 유형 매핑 기능 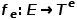 과 연결됩니다.
과 연결됩니다. 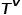 은 노드 유형의 집합을 나타내고,
은 노드 유형의 집합을 나타내고, 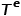 은 에지 유형의 집합을 나타냅니다.
은 에지 유형의 집합을 나타냅니다.
개념 2 동형 그래프:
그래프 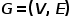 , 여기서
, 여기서 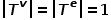 . 즉, 모든 노드는 하나의 유형에 속하고 모든 에지는 하나의 유형에 속합니다. 예를 들어 소셜 네트워크의 사용자 관심 관계 그래프에는 하나의 노드 유형인 사용자와 하나의 에지 유형인 주의 관계만 있습니다.
. 즉, 모든 노드는 하나의 유형에 속하고 모든 에지는 하나의 유형에 속합니다. 예를 들어 소셜 네트워크의 사용자 관심 관계 그래프에는 하나의 노드 유형인 사용자와 하나의 에지 유형인 주의 관계만 있습니다.
개념 3 이종 그래프:
그래프 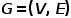 , 여기서
, 여기서 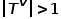 또는
또는 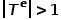 . 즉, 하나 이상의 노드 유형 또는 에지 유형이 있습니다. 예를 들어 학술 네트워크의 그래프 구조에는 논문, 저자 및 컨퍼런스와 같은 여러 노드 유형이 있습니다. 저자와 논문, 논문과 학회 간의 출판 관계, 논문 간의 인용 관계 등.
. 즉, 하나 이상의 노드 유형 또는 에지 유형이 있습니다. 예를 들어 학술 네트워크의 그래프 구조에는 논문, 저자 및 컨퍼런스와 같은 여러 노드 유형이 있습니다. 저자와 논문, 논문과 학회 간의 출판 관계, 논문 간의 인용 관계 등.
개념 4 1차 유사성:
두 노드를 연결하는 간선의 가중치가 클수록 두 노드 사이의 1차 유사도도 더 커집니다. 노드 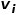 와 노드
와 노드 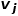 사이의 1차 유사성은
사이의 1차 유사성은 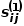 로 표현됩니다. 여기서
로 표현됩니다. 여기서 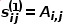 이 있습니다. 노드입니다
이 있습니다. 노드입니다 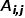 및 노드
및 노드 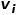 사이의 가장자리
사이의 가장자리 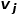 의 무게입니다.
의 무게입니다.  개념 5 2차 유사성:
개념 5 2차 유사성:
인접한 두 노드의 네트워크 구조가 유사할수록 두 노드 간의 2차 유사성은 더 커집니다. 2차 유사성
과 노드 그림 1 2차 유사성의 도식 개념 6 그래프 임베딩: 입력 그래프와 사전 정의된 임베딩 차원이 주어지면 그래프 임베딩이 효율적입니다. 가능한 한 그래프 속성을 유지하면서 그래프를 차원 공간으로 변환합니다. 그래프를 표현하기 위해 차원 벡터 또는 파트 03 ● 그래프 임베딩 알고리즘 분류 ● 지난 수십 년 동안 , 연구자들은 소셜 네트워크, 통신 네트워크 및 기타 시나리오에 상당한 영향을 미치는 것으로 입증된 많은 우수한 알고리즘을 제안했습니다. 업계에서는 일반적으로 이러한 그래프 임베딩 알고리즘을 출력 세분성 차이에 따라 다음 세 가지 범주로 나눕니다. 차원 공간 그래프의 각 노드를 나타내는 "유사한" 노드의 임베딩 벡터 표현도 유사합니다. 그래프의 노드를 분석한 후 노드 분류 또는 노드 클러스터링과 같은 작업을 수행해야 하는 경우 일반적으로 노드 임베딩이 선택됩니다. (2) Edge Embedding 은 벡터를 사용하여 저차원 공간에서 그래프의 각 모서리를 나타냅니다. 에지는 노드 쌍으로 구성되며 일반적으로 노드 쌍 관계를 나타냅니다. 엣지 임베딩은 그래프의 엣지를 분석하고 지식 그래프 관계 예측이나 링크 예측 등의 작업을 수행해야 하는 경우에 적합합니다. (3) 그래프 임베딩 벡터를 사용하여 저차원 공간, 일반적으로 분자나 단백질과 같은 작은 그래프에서 전체 그래프를 나타냅니다. 그래프를 벡터로 표현하면 서로 다른 그래프 간의 유사성을 쉽게 계산할 수 있어 그래프 분류 문제가 해결됩니다. 다양한 작업 요구 사항에 따라 선택되는 그래프 임베딩 알고리즘이 결정됩니다. 공간상의 이유로 여기에서는 비교적 자세한 학습을 위해 노드 임베딩의 DeepWalk 알고리즘과 Node2Vec 알고리즘을 발췌했습니다. 파트 04 ● ● 분야의 word2vec 아이디어에서 영감을 얻었습니다. 자연어 처리, Perozzi 등은 그래프에서 노드 표현 벡터를 학습하기 위한 모델을 구축하고 노드 간의 동시 발생 관계를 코퍼스 알고리즘의 단어 간의 동시 발생 관계로 유추하기 위해 DeepWalk를 제안했습니다. 그래프 내 노드들의 이웃 노드 시퀀스는 랜덤 워크(Random Walk)를 통해 수집되는데, 이는 노드 컨텍스트 코퍼스와 동일하며, 이를 통해 그래프 내 노드 간 동시 발생 관계 추출 문제를 해결할 수 있습니다. 노드 시퀀스의 길이와 시작점을 미리 설정합니다. 랜덤 워크 전략은 이웃 노드 중에서 다음 워킹 노드를 결정하는 방법을 안내합니다. 이 단계를 반복하여 조건을 충족하는 시퀀스를 얻습니다. 그림. 2. 쇼. 그림 2 랜덤 워크의 개략도 word2vec 알고리즘의 단어는 그래프 노드의 잠재 특징 표현을 추가로 학습하기 위해 DeepWalk 알고리즘은 그래프의 노드를 확률 계산도 word2vec 알고리즘의 스킵 그램 모델을 참조해야 합니다. 그림 3에서 볼 수 있듯이 스킵 그램 모델에는 두 개의 키 행렬이 포함되어 있습니다. 하나는 중심 단어 벡터 행렬 랜덤 워크 과정에서는 샘플링 시퀀스에서 노드 간의 순차적 관계를 고려하지 않으므로 노드 간의 근접 관계를 더 잘 반영하고 계산 비용을 줄일 수 있습니다. 그림 3 스킵 그램 모델 다이어그램 2. Node2Vec 알고리즘 DeepWalk 알고리즘을 기반으로 연구원 Grover A와 Leskovec J가 Node2Vec 알고리즘을 제안했습니다. Node2Vec 알고리즘은 DeepWalk 알고리즘에서 랜덤 워크를 통해 노드 시퀀스를 생성하는 프로세스를 최적화합니다. 이는 매개변수 여기서 그림 4 Node2Vec 랜덤 워크 전략의 개략도 Node2Vec의 랜덤 워크 전략은 그림 4와 같이 두 가지 매개변수를 기반으로 제어됩니다. 노드 v가 edge 일 때 노드 (2) (3) 정보기술의 급속한 발전으로 네트워크 환경은 점점 더 복잡해지고 있으며, 그 중에서도 APT 공격의 발생률이 높아 기업이 주의해야 할 보안 문제입니다. 실제로 APT 공격이 발생하는 기본 환경인 네트워크는 그 자체로 컴퓨터와 기타 요소들로 구성된 네트워크 구조이다. 공격 감지 문제를 노드, 에지 또는 그래프의 하위 그래프 분류 작업으로 분류합니다. 그래프 임베딩은 훌륭한 연구 공간이 있는 풍부한 문제입니다. 모델 훈련 효율성을 개선하고, 모델 구성 방법을 혁신하고, 그래프 임베딩 아이디어를 더 많은 생산 사례에 적용하는 방법은 더 나은 솔루션을 찾기 위해 더 많은 연구가 필요합니다. 참고자료 [1]Xu M. 그래프 삽입 방법 및 응용 이해[J] SIAM Review, 2021, 63(4): 825-853. [2] Cai H, Zheng V W, Chang K C C. 그래프 임베딩에 대한 종합 조사: 문제, 기술 및 응용[J]. IEEE Transactions on Knowledge and Data Engineering, 2018, 30(9): 1616-1637 . [3]Goyal P, Ferrara E. 그래프 임베딩 기술, 애플리케이션 및 성능: 설문조사[J], Knowledge-Based Systems, 2018, 151: 78-94.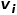 은
은 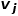 과 의
과 의 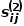 동네입니다.
동네입니다. 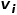 의 동네
의 동네 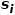 의 유사점. 그림 1과 같이 노드 f와 노드 g를 연결하는 간선이 있으므로 노드 f와 노드 g는 1차 유사합니다. 노드 e와 노드 g를 연결하는 간선은 없지만 4개의 동일한 이웃 노드가 있으므로 노드 e와 노드 g는 2차 유사합니다.
의 유사점. 그림 1과 같이 노드 f와 노드 g를 연결하는 간선이 있으므로 노드 f와 노드 g는 1차 유사합니다. 노드 e와 노드 g를 연결하는 간선은 없지만 4개의 동일한 이웃 노드가 있으므로 노드 e와 노드 g는 2차 유사합니다. 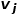
 차원 벡터 세트를 사용하여 그래프 속성의 보존 정도를 정량화하기 위해 1차 유사성 또는 고차 유사성에 의존합니다. 각 벡터는 그래프의 일부 임베딩을 나타냅니다. 노드 또는 가장자리와 같은 그래프.
차원 벡터 세트를 사용하여 그래프 속성의 보존 정도를 정량화하기 위해 1차 유사성 또는 고차 유사성에 의존합니다. 각 벡터는 그래프의 일부 임베딩을 나타냅니다. 노드 또는 가장자리와 같은 그래프. 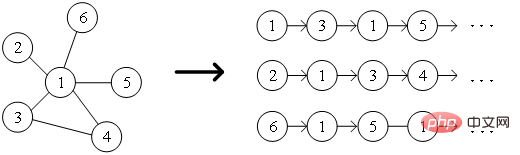
 의 노드에 해당하고, 단어 시퀀스는 다음에서 얻은 노드 시퀀스에 해당합니다. Random Walk, A Random Walk
의 노드에 해당하고, 단어 시퀀스는 다음에서 얻은 노드 시퀀스에 해당합니다. Random Walk, A Random Walk 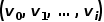 에 대해 공식에 표시된 대로 최적화 목적 함수를 정의합니다.
에 대해 공식에 표시된 대로 최적화 목적 함수를 정의합니다. 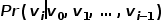
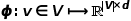 차원 벡터에 매핑하는 매핑 기능
차원 벡터에 매핑하는 매핑 기능 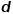 을 도입합니다. , 그러면 문제는 다음 공식의 확률을 추정하기 위해 변환됩니다.
을 도입합니다. , 그러면 문제는 다음 공식의 확률을 추정하기 위해 변환됩니다. 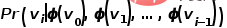
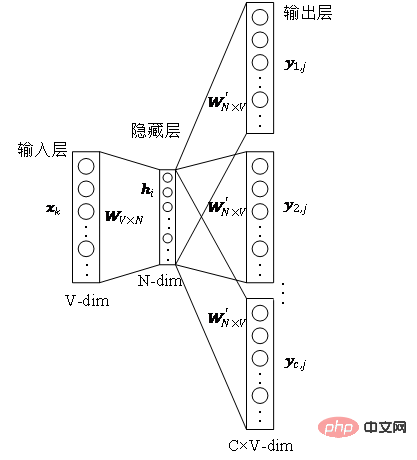
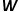 이고 다른 하나는 배경 단어 벡터 행렬
이고 다른 하나는 배경 단어 벡터 행렬  입니다. 가중치 행렬은 각각 단어와 연관된 단어 벡터를 서로 다른 역할로 나타냅니다. 스킵그램(Skip-gram)은 단어 문맥을 예측하는 모델이다. 코퍼스로부터 단어 간의 관계를 먼저 학습한 후, 이 관계를 이용하여 특정 단어의 문맥, 즉 단어의 벡터 표현을 표현한다. 즉, 동일한 순서에서 두 단어가 동시에 나타나는 빈도가 높을수록 두 단어의 벡터 표현이 더 유사합니다. 이 아이디어를 그래프에 적용하고 공식에 표시된 대로 최적화 목적 함수를 정의합니다.
입니다. 가중치 행렬은 각각 단어와 연관된 단어 벡터를 서로 다른 역할로 나타냅니다. 스킵그램(Skip-gram)은 단어 문맥을 예측하는 모델이다. 코퍼스로부터 단어 간의 관계를 먼저 학습한 후, 이 관계를 이용하여 특정 단어의 문맥, 즉 단어의 벡터 표현을 표현한다. 즉, 동일한 순서에서 두 단어가 동시에 나타나는 빈도가 높을수록 두 단어의 벡터 표현이 더 유사합니다. 이 아이디어를 그래프에 적용하고 공식에 표시된 대로 최적화 목적 함수를 정의합니다. 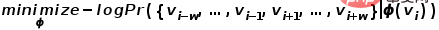
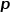 및 매개변수
및 매개변수 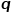 를 정의하여 각 랜덤 워크가 너비 우선 샘플링인지 깊이 우선 샘플링인지 안내합니다. 샘플링하므로 적응성이 높습니다. 현재 노드
를 정의하여 각 랜덤 워크가 너비 우선 샘플링인지 깊이 우선 샘플링인지 안내합니다. 샘플링하므로 적응성이 높습니다. 현재 노드 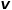 를 방문했다고 가정하면 다음 노드
를 방문했다고 가정하면 다음 노드 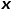 를 방문할 확률은 수식과 같습니다.
를 방문할 확률은 수식과 같습니다. 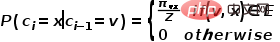
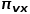 는 노드
는 노드 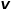 에서 노드
에서 노드 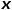 로의 전환 확률을 나타내고
로의 전환 확률을 나타내고 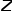 은 정규화 상수를 나타냅니다.
은 정규화 상수를 나타냅니다. 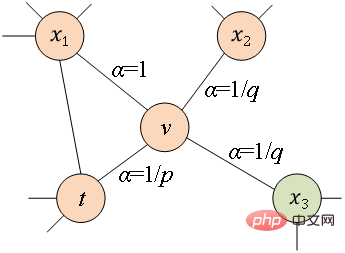
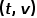 를 통해 도달했다고 가정하고 다음 단계는 노드 오른쪽을 방문하는 것입니다. 즉, 그래프가 비가중 그래프인 경우
를 통해 도달했다고 가정하고 다음 단계는 노드 오른쪽을 방문하는 것입니다. 즉, 그래프가 비가중 그래프인 경우 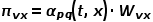 이 노드의 전환 확률을 직접 결정합니다. 그래프가 가중치 그래프인 경우
이 노드의 전환 확률을 직접 결정합니다. 그래프가 가중치 그래프인 경우 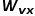 과 간선 가중치
과 간선 가중치 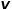 의 곱이 노드의 최종 전환 확률을 결정합니다.
의 곱이 노드의 최종 전환 확률을 결정합니다. 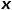 은 다음 공식에 따라 계산할 수 있습니다. 여기서
은 다음 공식에 따라 계산할 수 있습니다. 여기서 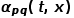 은 노드
은 노드 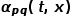 과 노드
과 노드 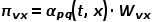 사이의 최단 경로 거리입니다.
사이의 최단 경로 거리입니다. 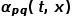 방황 샘플이
방황 샘플이 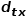 노드에서
노드에서 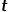 노드로 이동하고 다음 홉 노드를 선택해야 하는 경우 다음 세 가지 상황이 발생합니다.
노드로 이동하고 다음 홉 노드를 선택해야 하는 경우 다음 세 가지 상황이 발생합니다. 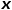 (1)
(1) 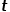 을 반환합니다.
을 반환합니다. 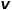
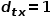 인 경우 노드
인 경우 노드 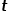 과 노드
과 노드 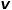 의 공통 인접 노드(예: node
의 공통 인접 노드(예: node 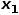 )를 선택합니다.
)를 선택합니다. 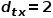 일 때, 노드
일 때, 노드 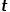 와 같이 노드
와 같이 노드 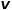 와 관련이 없는 노드
와 관련이 없는 노드 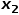 의 인접 노드를 선택합니다.
의 인접 노드를 선택합니다. 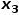 또는
또는 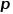 즉,
즉, 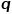 매개변수는 이전 홉 노드로 돌아올 확률을 제어하고,
매개변수는 이전 홉 노드로 돌아올 확률을 제어하고, 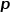 매개변수는 로컬 구조 정보를 탐색할지 전역 구조 정보를 탐색할지 여부를 더 많이 제어합니다. 네트워크의 DeepWalk
매개변수는 로컬 구조 정보를 탐색할지 전역 구조 정보를 탐색할지 여부를 더 많이 제어합니다. 네트워크의 DeepWalk 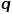 및
및
위 내용은 그래프 임베딩 알고리즘에 대한 간략한 논의의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!