스탠포드와 버클리의 새로운 연구가 구글의 '양자 우위'를 무너뜨렸습니다! 이론적으로는 아름답지만 실제로는 쓸모가 없습니다.
양자우월주의, 이 용어가 나온지 거의 4년이 되었습니다.
2019년 Google 물리학자들은 53큐비트 머신으로 양자 헤게모니를 성공적으로 달성했다고 발표했는데, 이는 중요한 상징적 이정표였습니다.
네이처에 발표된 논문에서는 양자 시스템이 계산을 완료하는 데 고작 200초밖에 걸리지 않았는데, 당시 가장 강력한 슈퍼컴퓨터인 서밋을 사용해 동일한 계산을 수행하는 데 약 1만년이 걸렸다고 명시했습니다.

양자우월이란 무엇인가요?
소위 "양자 우월" 또는 "양자 우위"(이하 "양자 우월")는 양자 컴퓨터가 완료할 수 있는 작업이 실현 가능한 기존 알고리즘의 범위를 벗어남을 의미합니다.
이러한 작업이 가장 발전된 전통적인 슈퍼컴퓨터에 배치되더라도 긴 계산 시간(종종 수천 년)으로 인해 알고리즘의 실질적인 중요성이 상실됩니다.
흥미롭게도 구글의 2019년 결과에서는 양자 헤게모니가 달성됐다고만 기술했을 뿐, 양자컴퓨터가 클래식 컴퓨터를 능가한 구체적인 사례는 설명하지 않았다.
현재 양자컴퓨터는 양자컴퓨팅의 성능과 안정성을 누적하고 훼손할 수 있는 오류로 인해 어려움을 겪고 있기 때문에 대답하기 어려운 질문입니다.
사실 양자 헤게모니 실현 분야에 비해 과학자들이 더 알고 싶어하는 것은 양자 컴퓨터가 점점 더 커지면서 기존 알고리즘이 따라잡을 수 있을지에 대한 또 다른 질문입니다.

텍사스 대학교 오스틴 캠퍼스의 컴퓨터 과학자 Scott Aaronson은 "우리는 결국 양자 측면이 완전히 거리를 두고 이 경쟁을 완전히 끝내기를 희망합니다."라고 말했습니다.
대부분의 연구자들은 , 대답은 부정적입니다.
즉, 언젠가는 기존 알고리즘이 양자 컴퓨팅의 속도를 완전히 따라갈 수 없게 되지만, 이를 정확하고 종합적으로 증명하지 못했습니다. 이러한 추론을 확실하게 증명하는 한 가지 방법은 양자 컴퓨팅이 기존 컴퓨팅보다 "지속적인 이점"을 얻을 수 있는 조건을 찾는 것입니다.
이제 이 질문에는 예비적인 답이 있는 것 같습니다.
시간 절약: 양자 컴퓨팅은 오류 수정을 계속할 수 없으면 이러한 오류는 이상적인 "양자 헤게모니"를 깨뜨리게 됩니다.” 양자 알고리즘을 따라가는 알고리즘.

최근 Arxiv에 게재된 사전 인쇄 논문에서 하버드 대학, 캘리포니아 대학, 버클리 대학, 이스라엘 히브리 대학의 공동 팀은 이 결론을 확인하기 위한 큰 진전을 이루었습니다.
그들은 표적 오류 수정이 무작위 회로 샘플링에서 내구성 있는 양자 우위를 위한 필수 조건임을 입증했으며, 이는 몇 년 전 Google의 연구 결론을 뒷받침합니다. 현재의 양자 오류 수정 수준에서는 양자 우위가 실제로 존재하지 않습니다.
더 이상 양자 우월성을 위한 "골든 존"은 없습니다
연구원들은 이 결론을 증명하기 위해 오류가 존재할 때 무작위 회로 샘플링 실험을 시뮬레이션할 수 있는 고전적인 알고리즘을 개발했습니다.
큐비트 배열로 시작하고 "양자 게이트"라는 작업을 사용하여 이러한 큐비트를 무작위로 조작합니다. 일부 양자 게이트는 큐비트 쌍을 얽히게 합니다. 즉, 큐비트는 개별적으로 설명할 수 없는 양자 상태를 공유합니다.
다층 회로에 이러한 양자 게이트를 반복적으로 설정하면 큐비트가 더 복잡한 얽힌 상태로 들어갈 수 있습니다.
이 양자 상태를 이해하기 위해 연구원들은 어레이의 모든 큐비트를 측정했습니다. 이 동작으로 인해 모든 큐비트의 집합적인 양자 상태가 일반 비트의 임의 문자열, 즉 0과 1로 축소됩니다.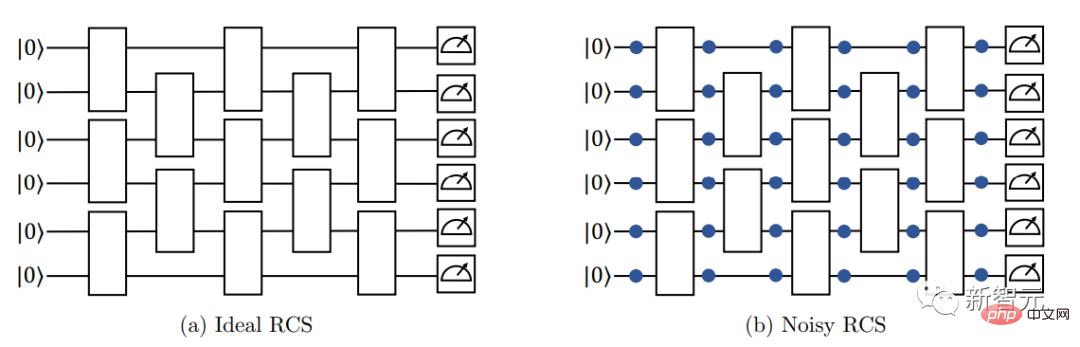
배열의 큐비트 수에 따라 가능한 결과의 수가 빠르게 증가합니다. Google의 2019년 실험에서는 53큐비트에 거의 10조 개의 결과가 포함되었습니다.
게다가 이 방법은 결과의 확률 분포 맵을 구축하기 위해 무작위 회로에서 여러 번 반복 측정해야 합니다.
양자 우월성에 대한 질문은 얽힘을 사용하지 않는 고전적인 알고리즘으로 이러한 확률 분포를 모방하는 것이 어렵거나 심지어 불가능합니까?
2019년 Google 연구원들은 오류가 발생하지 않는 오류 없는 양자 회로에서는 이 목표가 어렵다는 것을 증명했습니다. 오류 없이 고전적인 알고리즘을 사용하여 무작위 회로 샘플링 실험을 시뮬레이션하는 것은 실제로 어렵습니다.
계산 복잡도의 관점에서 볼 때, 큐비트 수가 증가하면 기존 분류 알고리즘의 계산 복잡도는 기하급수적으로 증가하는 반면, 양자 알고리즘의 계산 복잡도는 다항식으로 증가합니다.
n이 충분히 커지면 n에서 지수 함수인 알고리즘은 n에서 다항식인 알고리즘보다 훨씬 뒤떨어집니다.
이것이 고전 컴퓨터에서는 어렵지만 양자 컴퓨터에서는 쉬운 문제를 이야기할 때 언급하는 차이점입니다. 최고의 클래식 알고리즘은 기하급수적인 시간이 걸리는 반면, 양자 컴퓨터는 다항식 시간에 문제를 해결할 수 있습니다.
그러나 2019년 논문은 불완전한 양자 게이트로 인한 오류의 영향을 고려하지 않았으며, 연구 결론은 실제로 오류 수정 없이 무작위 회로 샘플링이 여전히 양자 헤게모니를 달성할 수 있는지에 대한 공백을 남겼습니다.
실제로 양자 얽힘에서 발생하는 누적 오류를 고려하면 기존 알고리즘으로 무작위 회로 샘플링 실험을 시뮬레이션하는 어려움이 크게 줄어들 것입니다. 그리고 기존 알고리즘 시뮬레이션의 계산 복잡성이 양자 알고리즘과 동일한 다항식 수준으로 감소되면 양자 헤게모니는 더 이상 존재하지 않습니다.
이 새로운 논문은 회로 깊이가 일정하게 유지된다고 가정할 때(예: 매우 얕은 3개 층) 큐비트 수가 증가함에 따라 양자 얽힘이 너무 많지 않고 출력이 여전히 고전적으로 시뮬레이션될 수 있음을 보여줍니다.
반면, 증가하는 큐비트 수를 따라가기 위해 회로 깊이를 늘리면 양자 게이트 오류의 누적 효과로 인해 얽힘으로 인한 복잡성이 희석되고 시뮬레이션하기가 더 쉬워집니다. 고전적인 알고리즘으로 출력합니다.
둘 사이에는 '골든 존'이 있습니다. 즉, 양자 헤게모니가 계속해서 생존할 수 있는 창, 즉 기존 알고리즘 시뮬레이션이 양자 얽힘을 따라잡을 수 없는 범위입니다.
본 논문이 출판되기 전에는 큐비트 수가 증가하더라도 큐비트 수가 특정 중간 범위에 도달하면 양자 우위가 여전히 존재했습니다.
이 회로 깊이에서는 양자 알고리즘 오류로 인해 출력이 꾸준히 저하되더라도 모든 단계에서 기존 알고리즘을 시뮬레이션하기가 어렵습니다.
이 새로운 논문은 이 "골든 존"을 거의 제거했습니다.
이 논문은 무작위 회로 샘플링을 시뮬레이션하기 위한 고전적인 알고리즘을 도출하고 그 실행 시간이 지수 함수가 아니라 해당 양자 실험을 실행하는 데 필요한 시간의
다항 함수임을 증명합니다. 이 결과는 고전적 무작위 회로 샘플링 방식의 속도와 양자 방식의 속도 사이에 밀접한 이론적 연관성을 확립합니다. 즉, 이론적으로 달성된 양자 헤게모니가 실제로는 거의 존재하지 않음을 선언합니다.
내가 "거의"라고 말하는 이유는 새로운 알고리즘의 기본 가정이 일부 얕은 회로에서는 유효하지 않아 알 수 없는 "작은 간격"을 남기기 때문입니다.
그러나 이러한 격차에서 양자 우위를 달성할 희망을 품고 있는 연구자는 여전히 거의 없습니다. 심지어 시카고 대학의 컴퓨터 과학자이자 2019년 구글 논문의 저자 중 한 명인 빌 페퍼먼(Bill Fefferman)도 "가능성은 매우 희박하다고 생각합니다"라고 말했습니다.
계산 복잡도 이론의 엄격한 기준에 따르면 무작위 회로 샘플링은 더 이상 양자 우월성을 생성하지 않는다고 말할 수 있습니다.
또한 이러한 결론에 직면하여 모든 연구자들은 양자 오류 수정이 양자 컴퓨팅의 장기적인 성공에 얼마나 중요한지에 동의합니다. Fefferman은 "결국 우리는 양자 오류 수정이 해결책이라는 것을 발견했습니다."라고 말했습니다.
위 내용은 스탠포드와 버클리의 새로운 연구가 구글의 '양자 우위'를 무너뜨렸습니다! 이론적으로는 아름답지만 실제로는 쓸모가 없습니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7552
7552
 15
15
 1382
1382
 52
52
 83
83
 11
11
 59
59
 19
19
 22
22
 95
95
 모델, 데이터 및 프레임워크에 대한 심층 분석: 효율적인 대규모 언어 모델에 대한 철저한 54페이지 검토
Jan 14, 2024 pm 07:48 PM
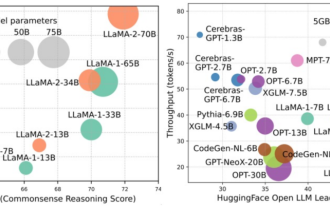
모델, 데이터 및 프레임워크에 대한 심층 분석: 효율적인 대규모 언어 모델에 대한 철저한 54페이지 검토
Jan 14, 2024 pm 07:48 PM
대규모 언어 모델(LLM)은 자연어 이해, 언어 생성, 복잡한 추론을 비롯한 여러 중요한 작업에서 강력한 기능을 입증했으며 사회에 지대한 영향을 미쳤습니다. 그러나 이러한 뛰어난 기능을 사용하려면 상당한 교육 리소스(왼쪽 참조)와 긴 추론 시간(오른쪽 참조)이 필요합니다. 따라서 연구자들은 효율성 문제를 해결하기 위한 효과적인 기술적 수단을 개발해야 합니다. 또한 그림의 오른쪽에서 볼 수 있듯이 Mistral-7B와 같은 일부 효율적인 LLM(LanguageModel)이 LLM의 설계 및 배포에 성공적으로 사용되었습니다. 이러한 효율적인 LLM은 LLaMA1-33B와 유사한 정확도를 유지하면서 추론 메모리를 크게 줄일 수 있습니다.
 Nvidia의 차세대 GPU, H100을 깨다 공개! 2024년에 공개된 최초의 3nm 멀티칩 모듈 디자인
Sep 30, 2023 pm 12:49 PM
Nvidia의 차세대 GPU, H100을 깨다 공개! 2024년에 공개된 최초의 3nm 멀티칩 모듈 디자인
Sep 30, 2023 pm 12:49 PM
3nm 공정, H100을 능가하는 성능! 최근 외신 디지타임스는 엔비디아가 차세대 GPU인 B100(코드명 '블랙웰')을 인공지능(AI)과 고성능컴퓨팅(HPC) 애플리케이션용 제품으로 개발 중이라는 소식을 전했다. B100은 TSMC의 3nm 공정 공정과 더욱 복잡한 MCM(멀티 칩 모듈) 설계를 사용하며 2024년 4분기에 출시될 예정입니다. 인공지능 GPU 시장의 80% 이상을 독점하고 있는 엔비디아의 경우, B100을 이용해 철이 뜨거울 때 공격할 수 있고, 이번 AI 배치 물결에서 AMD, 인텔 등 도전자들을 더욱 공격할 수 있다. NVIDIA 추정에 따르면, 2027년까지 이 분야의 출력 가치는 대략적으로 도달할 것으로 예상됩니다.
 확산 + 초해상도 모델의 강력한 조합, Google 이미지 생성기의 기술 Imagen
Apr 10, 2023 am 10:21 AM
확산 + 초해상도 모델의 강력한 조합, Google 이미지 생성기의 기술 Imagen
Apr 10, 2023 am 10:21 AM
최근에는 다중모달 학습이 많은 주목을 받고 있는데, 특히 텍스트-이미지 합성과 이미지-텍스트 대조 학습이라는 두 가지 방향에서 더욱 그렇습니다. OpenAI에서 출시한 텍스트 이미지 모델 DALL・E 및 DALL-E 2, NVIDIA의 GauGAN 및 GauGAN2와 같은 일부 AI 모델은 창의적인 이미지 생성 및 편집에 적용되어 광범위한 대중의 관심을 끌었습니다. 이에 뒤처지지 않기 위해 Google은 5월 말 자체 텍스트-이미지 모델 Imagen을 출시했는데, 이는 캡션 조건부 이미지 생성의 범위를 더욱 확장하는 것으로 보입니다. 장면에 대한 설명만 주어지면 Imagen은 고품질, 고해상도를 생성할 수 있습니다.
 다중 모드 대형 모델에 대한 가장 포괄적인 리뷰가 여기에 있습니다! 마이크로소프트 연구원 7명 적극 협력, 5개 주요 주제, 119페이지 분량의 문서
Sep 25, 2023 pm 04:49 PM
다중 모드 대형 모델에 대한 가장 포괄적인 리뷰가 여기에 있습니다! 마이크로소프트 연구원 7명 적극 협력, 5개 주요 주제, 119페이지 분량의 문서
Sep 25, 2023 pm 04:49 PM
다중 모드 대형 모델에 대한 가장 포괄적인 리뷰가 여기에 있습니다! Microsoft의 중국 연구원 7명이 집필한 이 책은 119페이지로 구성되어 있습니다. 이는 이미 완성되어 현재까지 선두에 있는 두 가지 유형의 다중 모드 대형 모델 연구 방향에서 시작하여 시각적 이해와 시각적 생성이라는 5가지 구체적인 연구 주제를 포괄적으로 요약합니다. 통합 시각적 모델 LLM이 지원하는 다중 모드 대형 모델 다중 모드 에이전트는 현상에 초점을 맞춥니다. 다중 모드 기본 모델은 전문화된 모델에서 범용 모델로 이동했습니다. Ps. 그래서 저자는 논문 서두에 도라에몽의 이미지를 직접 그렸습니다. 이 리뷰(보고서)를 누가 읽어야 합니까? Microsoft의 원래 말로: 전문 연구원이든 학생이든 다중 모달 기본 모델의 기본 지식과 최신 진행 상황을 배우는 데 관심이 있는 한 이 콘텐츠는 함께 모이는 데 매우 적합합니다.
 새로운 연구는 한계를 극복하는 데 있어 신경망을 능가하는 양자 몬테카를로의 잠재력을 밝혔으며, Nature 하위 이슈에서는 최신 진행 상황을 자세히 설명합니다.
Apr 24, 2023 pm 09:16 PM
새로운 연구는 한계를 극복하는 데 있어 신경망을 능가하는 양자 몬테카를로의 잠재력을 밝혔으며, Nature 하위 이슈에서는 최신 진행 상황을 자세히 설명합니다.
Apr 24, 2023 pm 09:16 PM
4개월 후, ByteDance Research와 북경 대학교 물리학과 Chen Ji 연구 그룹의 또 다른 공동 작업이 최고의 국제 저널 Nature Communications에 게재되었습니다: "Towards the ground state of Molecular via 확산 몬테 카를로 신경망"이라는 논문 신경망과 확산 몬테카를로 방법을 결합하여 양자 화학에서 신경망 방법의 적용을 크게 향상시켰으며 관련 작업에 대한 계산 정확도, 효율성 및 시스템 규모가 최신 SOTA가 되었습니다. 논문 링크: https://www.nature.com
 SD 커뮤니티의 I2V 어댑터: 구성이 필요하지 않으며 플러그 앤 플레이, Tusheng 비디오 플러그인과 완벽하게 호환됩니다.
Jan 15, 2024 pm 07:48 PM
SD 커뮤니티의 I2V 어댑터: 구성이 필요하지 않으며 플러그 앤 플레이, Tusheng 비디오 플러그인과 완벽하게 호환됩니다.
Jan 15, 2024 pm 07:48 PM
이미지-비디오 생성(I2V) 작업은 정적 이미지를 동적 비디오로 변환하는 것을 목표로 하는 컴퓨터 비전 분야의 과제입니다. 이 작업의 어려움은 이미지 콘텐츠의 신뢰성과 시각적 일관성을 유지하면서 단일 이미지에서 시간 차원의 동적 정보를 추출하고 생성하는 것입니다. 기존 I2V 방법에는 이 목표를 달성하기 위해 복잡한 모델 아키텍처와 많은 양의 교육 데이터가 필요한 경우가 많습니다. 최근 Kuaishou가 주도한 새로운 연구 결과 "I2V-Adapter: AGeneralImage-to-VideoAdapter for VideoDiffusionModels"가 발표되었습니다. 본 연구에서는 혁신적인 이미지-비디오 변환 방법을 소개하고 경량 어댑터 모듈을 제안합니다.
 VPR 2024 만점 시험지! Meta는 EfficientSAM을 제안합니다: 모든 것을 빠르게 분할하세요!
Mar 02, 2024 am 10:10 AM
VPR 2024 만점 시험지! Meta는 EfficientSAM을 제안합니다: 모든 것을 빠르게 분할하세요!
Mar 02, 2024 am 10:10 AM
EfficientSAM의 이 작업은 CVPR2024에 5/5/5점 만점으로 포함되었습니다! 작가는 그 결과를 아래 사진처럼 소셜미디어에 공유했습니다. 르쿤 튜링상 수상자도 이 작품을 강력 추천했습니다! 최근 연구에서 Meta 연구진은 SAM을 사용한 SAMI(Mask Image Pre-training)라는 새로운 개선된 방법을 제안했습니다. 이 방법은 MAE 사전 훈련 기술과 SAM 모델을 결합하여 고품질 사전 훈련된 ViT 인코더를 달성합니다. SAMI를 통해 연구자들은 모델의 성능과 효율성을 개선하고 비전 작업을 위한 더 나은 솔루션을 제공하려고 노력합니다. 이 방법의 제안은 컴퓨터 비전 및 딥 러닝 분야를 더욱 탐구하고 개발할 수 있는 새로운 아이디어와 기회를 제공합니다. 서로 다른 것을 결합하여
 2022 볼츠만상 발표: Hopfield Network 창립자가 수상
Aug 13, 2023 pm 08:49 PM
2022 볼츠만상 발표: Hopfield Network 창립자가 수상
Aug 13, 2023 pm 08:49 PM
2022년 볼츠만상을 수상한 두 명의 과학자가 발표되었습니다. 이 상은 IUPAP 통계물리학위원회(C3)가 통계물리학 분야에서 뛰어난 업적을 이룬 연구자를 표창하기 위해 제정한 것입니다. 우승자는 이전에 볼츠만상이나 노벨상을 수상한 적이 없는 과학자여야 합니다. 이 상은 1975년에 시작되었으며 통계 물리학의 창시자인 루트비히 볼츠만(Ludwig Boltzmann)을 기념하기 위해 3년마다 수여됩니다. 수상 이유: 자기 조직화의 정확한 해결을 포함하여 통계 물리학 분야에 대한 Deepak Dharistheoriginalstatement의 선구적인 공헌을 인정하여 수여됩니다. 중요 모델, 인터페이스 성장, 장애




