Python을 사용하여 RSA 암호화 및 암호 해독 구현

어제 [1] Python을 사용하여 RSA 알고리즘을 구현하는 방법을 보여주는 영어 기사를 봤습니다. RSA에 익숙하지 않은 친구도 이 기사를 읽을 수 있습니다. RSA가 무엇인지, RSA의 수학적 원리를 설명하고 간단한 예를 들어 설명하는 RSA 알고리즘 이해는 Quanzhihu에서 RSA를 이해하는 가장 쉬운 기사라고 할 수 있습니다(독자의 의견에서 나온 것입니다).

영어로 제공된 코드를 실행해보니 중국어를 암호화할 수 없는 것을 발견하여 중국어 암호화 및 복호화를 지원하도록 암호화 및 복호화 기능을 수정했습니다. 오늘 기사에서는 Python을 사용하여 RSA 암호화 및 암호 해독 프로세스를 구현하는 방법을 공유하여 RSA에 대한 직관적인 이해를 돕기 위해 코드의 무작위 소수 생성 알고리즘도 학습할 가치가 있습니다.

0. 효과 시연

먼저 효과를 살펴보겠습니다.

원문: "두더지가 있습니다, 거래를 종료하세요"

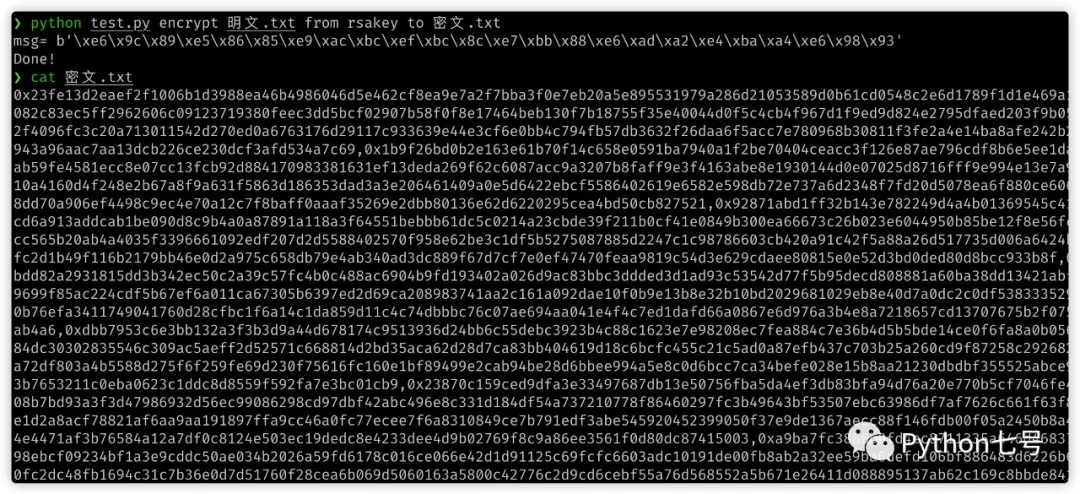
암호문은 전혀 해독되지 않습니다:

복호화 후:

전체 코드 공개 계정 "Python Seven" "rsa"라고 응답했습니다.

1. 키 쌍 생성

아이디어:

1) p와 q가 클수록 더 안전한 두 소수(소수)를 찾습니다.

p = genprime(1024)
q = genprime(1024)

genprime( ) 함수 구현 과정에 대해서는 이야기하지 않겠습니다.

2) 곱 n = p * q를 계산하고 오일러 함수 lamda_n을 계산합니다.

n = p * q
lambda_n = (p - 1) * (q - 1)

3) 1 < e < 람다_n이고 e와 람다_n이 상대적으로 소수인 경우 정수 e를 무작위로 선택합니다. 예를 들어 35537을 선택하는 경우 35537은 16비트만 포함하고 Lambda_n보다 작아야 합니다. < e < lambda_n，且 e 与 lambda_n 互质。比如选择 35537，35537 只有 16 位，必然小于 lambda_n。

e = 35537

4) e*d를lambda_n으로 나눈 나머지가 1이 되도록 정수 d를 찾아 키 쌍을 반환합니다.

d = eucalg(e, lambda_n)[0]
if d < 0: d += lambda_n
return (d, n), (e, n)

eucalg 함수 구현에 대해서는 나중에 논의하겠습니다.

이때 키 쌍 생성 기능은 다음과 같습니다.

def create_keys():
 p = genprime(1024)
 q = genprime(1024)
 n = p * q
 lambda_n = (p - 1) * (q - 1)
 e = 35537
 d = eucalg(e, lambda_n)[0]
 if d < 0: d += lambda_n
 return (d, n), (e, n)

2. 암호화 및 복호화 구현

암호화 및 복호화 과정은 동일하며 공개키 암호화, 개인키 복호화, 그 반대의 경우 개인키 키 암호화, 공개 키 복호화로 전자를 암호화, 후자를 서명이라고 합니다.

구체적인 함수 구현은 다음과 같습니다:

def encrypt_data(data,key):
e_data = []
for d in data:
 e = modpow(d, key[0], key[1]) 
 e_data.append(e)
return e_data

## 加密和解密的逻辑完全一样
decrypt_data = encrypt_data

여기서는 modpow 함수가 사용되며, 이는 공식 b^e % n = r을 계산하는 데 사용됩니다.

• 암호화 과정이라면 b는 평문, (n,e)는 공개키, r은 암호문이다.
• 복호화 프로세스라면 b는 암호문, (n, d)는 개인 키, r은 유명한 텍스트입니다.

modpow는 다음과 같이 정의됩니다.

def modpow(b, e, n):
 # find length of e in bits
 tst = 1
 siz = 0
 while e >= tst:
tst <<= 1
siz += 1
 siz -= 1
 # calculate the result
 r = 1
 for i in range(siz, -1, -1):
r = (r * r) % n
if (e >> i) & 1: r = (r * b) % n
 return r

3. 난수 생성 함수

알고리즘에서 수학의 중요성을 보여주는 행렬 곱셈과 피보나치 수열을 사용하는 난수 생성 함수입니다.

# matrix multiplication
def sqmatrixmul(m1, m2, w, mod):
 mr = [[0 for j in range(w)] for i in range(w)]
 for i in range(w):
for j in range(w):
 for k in range(w):
mr[i][j] = (mr[i][j] + m1[i][k] * m2[k][j]) % mod
 return mr

# fibonacci calculator
def fib(x, mod):
 if x < 3: return 1
 x -= 2
 # find length of e in bits
 tst = 1
 siz = 0
 while x >= tst:
tst <<= 1
siz += 1
 siz -= 1
 # calculate the matrix
 fm = [
# function matrix
[0, 1],
[1, 1]
 ]
 rm = [
# result matrix
# (identity)
[1, 0],
[0, 1]
 ]
 for i in range(siz, -1, -1):
rm = sqmatrixmul(rm, rm, 2, mod)
if (x >> i) & 1:
 rm = sqmatrixmul(rm, fm, 2, mod)

 # second row of resulting vector is result
 return (rm[1][0] + rm[1][1]) % mod

def genprime(siz):
 while True:
num = (1 << (siz - 1)) + secrets.randbits(siz - 1) - 10;
# num must be 3 or 7 (mod 10)
num -= num % 10
num += 3 # 3 (mod 10)
# heuristic test
if modpow(2, num - 1, num) == 1 and fib(num + 1, num) == 0:
 return num
num += 5 # 7 (mod 10)
# heuristic test
if modpow(2, num - 1, num) == 1 and fib(num + 1, num) == 0:
 return num

4. eucalg 함수 구현

함수의 본질은 다음 두 변수의 선형 방정식에 대한 해를 찾는 것입니다.

e * x - lambda_n * y =1

특정 코드:

def eucalg(a, b):
 # make a the bigger one and b the lesser one
 swapped = False
 if a < b:
a, b = b, a
swapped = True
 # ca and cb store current a and b in form of
 # coefficients with initial a and b
 # a' = ca[0] * a + ca[1] * b
 # b' = cb[0] * a + cb[1] * b
 ca = (1, 0)
 cb = (0, 1)
 while b != 0:
# k denotes how many times number b
# can be substracted from a
k = a // b
# swap a and b so b is always the lesser one
a, b, ca, cb = b, a-b*k, cb, (ca[0]-k*cb[0], ca[1]-k*cb[1])
 if swapped:
return (ca[1], ca[0])
 else:
return ca

5.Test

test.py 스크립트 사용 방법 :

1), 키 생성

python test.py make-keys rsakey

공개 키는 rsakey.pub에 저장되고, 개인 키는 rsakey.priv에 저장됩니다.

2), 파일 내용을 암호화합니다.

파일에 일반 텍스트가 있는 경우 .txt:

python test.py encrypt 明文.txt from rsakey to 密文.txt

는 ciphertext .txt를 생성합니다.

3. 파일 내용을 해독합니다

ciphertext.txt 파일이 있는 경우:

python test.py decrypt 密文.txt as rsakey to 解密后.txt

는 해독된 .txt를 생성합니다

최종 단어

이 문서에서는 간단한 내용을 공유합니다. RSA 알고리즘을 이해하는 데 도움이 될 수 있는 Python의 RSA 알고리즘 구현.

위 내용은 Python을 사용하여 RSA 암호화 및 암호 해독 구현의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!