튜링 머신: 컴퓨터가 없다면 어떻게 컴퓨팅에 관해 이야기할 수 있을까요?
1950년 10월, "기계는 생각할 수 있다"라는 제목의 논문이 출판되었습니다. 본 논문에서는 통신 장치를 통해 피험자에게 무작위로 질문을 하고, 테스터에게 질문함으로써 피험자(실제 사람과 기계)와 분리되는 무서운 테스트를 제안한다. 대화하고 있는 사람은 실제 사람이거나 기계였습니다.
여러 테스트를 거친 후 기계가 각 참가자의 평균 30% 이상의 오판을 만들 수 있다면 기계는 테스트를 통과했으며 인간 지능을 갖춘 것으로 간주됩니다.
이때 사람들은 로봇이 인간 지능을 가질 수 있다는 것을 처음 깨달았습니다. 이 테스트는 수백만 명의 SF 애호가들이 이야기하는 튜링 테스트입니다. 이 기사는 저자 Alan Turing에게 "인공지능의 아버지"라는 칭호를 주기도 했습니다.
인공지능으로 가는 길, 혹은 컴퓨터 발전 역사의 기원은 튜링이 24세 때 발표한 논문이다. 이 논문에서 그는 "계산 가능성"에 대해 엄격한 수학적 정의를 내리고 유명한 "튜링 머신" 아이디어를 제안했습니다. 튜링 기계는 특정 기계가 아니라 상상할 수 있는 모든 계산 기능을 계산하는 데 사용할 수 있는 매우 간단하지만 매우 강력한 컴퓨팅 장치를 만들 수 있는 정신 모델입니다.
튜링이 튜링 기계를 발명했기 때문에 때때로 누군가 튀어나와 튜링이 실제로 "컴퓨터를 발명했다"고 주장합니다. 그러나 Turing 기계는 실제 컴퓨팅 기계와 동일한 방식으로 설계되지 않았습니다. 튜링 기계는 기계의 추상 모델도 아닙니다. (튜링의 발언에서 알 수 있듯이) 튜링 기계는 테이블 위의 종이에 글을 쓰는 사람의 모델이라는 것이 밝혀졌습니다. 그렇다면 튜링은 왜 튜링 기계를 발명했으며, 튜링 기계는 우리를 어디로 이끌까요?
1 Turing의 논문 "On Computable Numbers"
이 질문에 답하는 가장 좋은 방법은 교과서를 옆으로 치워두고 논문을 펼치는 것입니다. 오늘날 1936년 간행물을 빌리는 데에는 대출 카드를 작성하거나 사서가 도서관에서 그것을 가져올 때까지 한 시간을 기다릴 필요가 없으며 손에 몰트 위스키 한 잔을 들고 집에서 Google에 쉽게 액세스할 수 있습니다. 우리가 찾고 있는 튜링 논문은 다음과 같습니다:

논문 주소: https://www.cs.virginia.edu/~robins/Turing_Paper_1936.pdf
에 일부 오류가 있습니다. 논문이지만 결점이 장점을 덮지는 않습니다. Joel David Hamkins가 말했듯이 Turing은 계산 가능한 실수를 계산 가능한 소수 확장이 있는 숫자로 정의했는데, 이는 실제로 작동하지 않지만 수정하는 것은 어렵지 않습니다.
Turing은 "계산 가능한 숫자와 "결정 문제"에서의 적용"이라는 제목으로 이 문서를 작성하려는 의도를 설명했습니다. "Entscheidungsproblem(결정 문제)"은 주어진 문제를 결정하는 효과적인 기술이 있는지 묻습니다. 1차 논리 공식은 유효합니다. 즉, 모든 해석이 참입니다.
튜링은 자신의 생각을 다음과 같이 확장했습니다.
실수를 계산하는 사람을 제한된 수만 만족시킬 수 있는 기계에 비교할 수 있습니다. 조건의 수 q1, q2,... qR.... 이 기계를 통과하는 긴 "종이 테이프"가 있고, 종이 테이프는 한 번에 한 조각씩 여러 부분으로 나누어지며, 우리는 이를 정사각형이라고 부릅니다. 각 사각형에는 "기호"가 포함될 수 있습니다. 작성된 기호 중 일부는 계산되는 실수의 10진수 순서를 형성하는 반면, 다른 기호는 단지 "기억 보조 도구"일 뿐입니다. 대략적인 메모는 지울 수 있습니다. 종이 위를 미끄러지며 그 기호로 뭔가를 하는 이 연산에는 수치 계산에 사용되는 연산이 모두 포함됩니다.
...
"계산 가능한 숫자"는 단순히 십진수로 표현되는 실수입니다. 내 정의에 따르면, 숫자가 소수 형태를 가지고 있다면, 그 표현이 기계로 기록될 수 있다면 그 숫자는 나중에 정의되고 증명됩니다. 이런 종류의 기사에서 독자들은 기사에 설명된 일부 메커니즘을 구현하는 방법에 대한 논의를 보고 싶어합니다. Turing의 제목과 기사에서 볼 수 있듯이 Turing은 주로 실제 계산에 관심이 있습니다. 소수점 이하 무한한 자리까지의 숫자. 이 문서에는 다른 많은 중요한 기여가 있습니다. 이 논문을 쓴 후 Turing은 이론 컴퓨팅 과학 분야의 문을 열었습니다. 이제 예리하고 생생하게 설계된 만능 튜링 기계가 생겼습니다. 수십 년 전 케임브리지 대학교에서 Ken Moody 박사는 Universal Minsky 키젠을 작성했습니다:
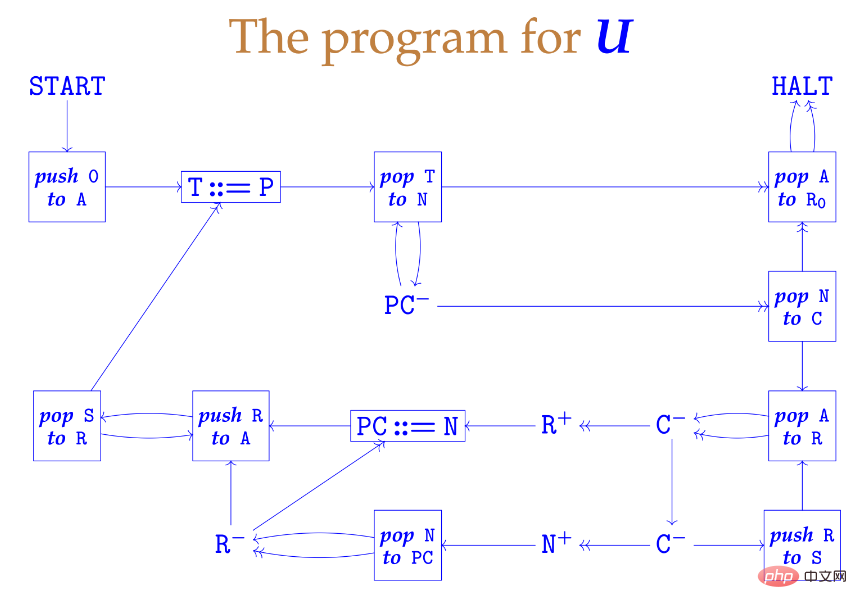
링크: http://www.igblan.free-online.co.uk/igblan/ca/minsky. html 이러한 기계에는 제한된 수의 레지스터가 있으며 각 레지스터에는 임의로 큰 음수가 아닌 정수를 저장할 수 있습니다. 여기에는 세 가지 다른 유형의 레이블이 지정된 명령어로 구성된 유한한 프로그램이 있습니다. 레지스터 증가 Moody는 N과 사이의 표준 전단사를 사용하여 정수 목록을 단일 정수로 압축합니다. 그는 스택을 밀어 올리고 내리는 등의 작업을 수행하는 작은 레지스터 머신의 작은 라이브러리를 작성하고 실제 프로세서의 가져오기-실행 주기를 연상시키는 디자인을 만들었습니다. 전체 프로세스는 다음 슬라이드에서 볼 수 있습니다. 아래 사진은 기계 자체입니다. 놀랍게도 이 기계의 구조는 너무 간단합니다! 3 정지 문제 Maurice Wilkes: 엔지니어는 저장 프로그램의 개념을 삼위일체와 유사한 중요한 이론으로 간주하고 이렇게 말할 것입니다. "이것은 절대적으로 일류이며 이렇게 해야 합니다. " 그 논문의 아이디어와 내가 말한 것 사이에는 실질적인 차이가 없습니다. 그는 그 논문을 출판하게 된 것은 행운이었습니다. 즉, Alonzo Church는 다른 방법을 사용해도 동일한 결과를 얻었습니다. 기사 주소: https://cacm.acm.org/magazines/2009/9/38898-an-interview-with-maurice-wilkes/fulltext
주의해야 할 점 , 인터뷰 당시 모리스 윌크스(Maurice Wilkes)는 96세였으며, 유명한 컴퓨터 선구자이자 EDSAC(전자 지연 저장 자동 계산기)의 아버지였습니다. 그의 이상한 대답에서 우리는 튜링의 높은 지위에 대한 질투를 엿볼 수 있다. 이 둘은 분명히 사이가 좋지 않습니다! 우리는 또한 이론에 대한 Maurice Wilkes의 경멸을 봅니다. 기계를 숫자로 인코딩하는 것은 저장된 프로그램 컴퓨터에서 예상되었지만 Turing의 작업은 순수한 수학이었고 공학적 중요성이 없었습니다. 튜링은 실제 컴퓨터 공학에 관심이 많았지만 실제 프로젝트에 참여하려는 그의 많은 시도는 좌절되었습니다. Church에 대한 그런 발언은 어떻게 평가하시나요? Turing과 Church는 프린스턴에 있었습니다
솔직히 이 문서는 읽기 어렵지만 거기까지 갈 수 있습니다. 그 상황. 이 기사에서는 람다 미적분학의 정의, 재귀 함수의 정의(Kleene/Gödel 의미) 및 람다 미적분학 판단 결과에서 패러다임의 존재 및 동등성에 대한 몇 가지 확실한 질문을 제공합니다. Church와 Craney는 람다 정의 함수와 재귀 함수 간의 동등성을 입증했으며, Turing이 프린스턴에 있는 동안 람다 정의 함수와 Turing 계산 가능 함수 간의 동등성도 입증되었으므로 Church-Turing 논문을 얻습니다. 효과적으로 계산할 수 있는 함수는 정확히 수학적 등가 클래스에 있는 함수라는 사실을 나타냅니다. 6 교회-튜링 논제가 맞나요? Ackermann 함수의 현대적인 형태는 다음과 같습니다: 기사 링크: https://lawrencecpaulson.github.io/2022/02/09/Ackermann-example.html f(n)=A(n,n)을 정의하면 짝수 f(4)를 계산할 것으로 기대할 수 없습니다. g(n)=A(4,n)은 원시 재귀이지만 계산이 거의 불가능합니다. 1930년대까지는 디지털 컴퓨터가 없었지만 효율적인 계산 가능성의 개념은 수학자들에게 잘 알려져 있었습니다. 타당도의 개념은 그리스 기하학의 직선 구조와 나침반 구조에서 오랫동안 등장해 왔습니다. 타당도는 결정 문제와 힐베르트의 열 번째 문제에서도 필수적인 부분입니다. 괴델의 재귀 함수와 처치의 람다 미적분학에 비해 튜링 개념의 천재성은 그것이 분명히 정확하다는 것입니다. 괴델 자신도 자신의 재귀 함수가 계산 개념을 포착했는지 확신하지 못했고, 처치의 생각이 맞는지도 알 수 없습니다. 튜링의 생각만이 단순하고 자연스러웠다. Turing의 아이디어는 다른 모델과 동등하다는 것이 입증되었으며 모든 모델에 대한 합리적인 설명을 제공합니다. 그는 1937년 논문 "계산 가능성 및 람다 정의 가능성"에서 이 사실을 지적했습니다. 이 글은 저자가 제안한 계산 가능한 함수와 Church의 λ 정의 함수와 Elbron과 Gödel이 제안하고 Klenny가 개발한 일반 재귀 함수가 동일함을 증명하는 것을 목표로 합니다. 이러한 동일한 함수는 모든 X 정의 함수가 계산 가능하며 모든 계산 가능한 함수가 일반적으로 재귀적임을 증명합니다. Turing은 "computable"이라고 썼지만 우리는 "Turing computable"이라고 써야 합니다.
2 튜링 기계의 목적은 책상에서 일하는 사무원을 시뮬레이션하는 것이고, 튜링 기계의 작동은 사무원의 작동과 동일하므로 기계에 기반한 주어진 변환 규칙 목록에 따라 이 작업 또는 저 작업을 수행합니다. 상태 및 테이프 기호 - 이러한 일상적인 작업을 수행하려면 튜링 기계가 분명히 필요합니다. 튜링의 논문은 건설의 세부 사항에 대해 약간 개략적이었지만 아무도 신경 쓰지 않는 것 같았습니다.


정지 문제는 확실히 결정할 수 없습니다. 그렇지 않으면 페르마의 마지막 정리와 같은 많은 수학적 추측을 해결하기 어려울 것입니다. x, y, z, n>2(예:
)를 검색하고 종료되는지 묻는 프로그램을 작성하세요. 그러나 정지의 불확실성은 엄격하게 표현되고 입증되어야 합니다. 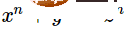 일반적인 믿음과는 달리 Turing의 논문은 정지 문제를 논의하지 않았지만 그가 "순환성"이라고 부르는 정지 문제와 관련된 특성을 논의했습니다. 튜링 기계는 "제한된 수의 첫 번째 기호(즉, 0과 1)만 쓴다"면 순환 기계입니다. 순환성이 중요한 이유는 튜링이 실수를 무한한 이진 문자열로 근사하는 것을 특히 좋아했기 때문이라고 생각합니다. 물리학자 크리스토퍼 스트레이치(Christopher Strachey)는 1965년 컴퓨터 저널에 보낸 편지에서 튜링이 정지 문제의 결정 불가능성에 대한 증거를 말했다고 주장했습니다.
일반적인 믿음과는 달리 Turing의 논문은 정지 문제를 논의하지 않았지만 그가 "순환성"이라고 부르는 정지 문제와 관련된 특성을 논의했습니다. 튜링 기계는 "제한된 수의 첫 번째 기호(즉, 0과 1)만 쓴다"면 순환 기계입니다. 순환성이 중요한 이유는 튜링이 실수를 무한한 이진 문자열로 근사하는 것을 특히 좋아했기 때문이라고 생각합니다. 물리학자 크리스토퍼 스트레이치(Christopher Strachey)는 1965년 컴퓨터 저널에 보낸 편지에서 튜링이 정지 문제의 결정 불가능성에 대한 증거를 말했다고 주장했습니다. 4 결정 문제에 관한 튜링의 1936년 논문의 중요성은 무엇입니까?
문서 링크: https://www.jstor.org/stable/2371045?origin=crossref

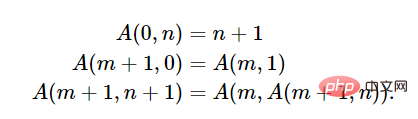
위 내용은 튜링 머신: 컴퓨터가 없다면 어떻게 컴퓨팅에 관해 이야기할 수 있을까요?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7569
7569
 15
15
 1386
1386
 52
52
 87
87
 11
11
 61
61
 19
19
 28
28
 107
107
 CUDA의 보편적인 행렬 곱셈: 입문부터 숙련까지!
Mar 25, 2024 pm 12:30 PM
CUDA의 보편적인 행렬 곱셈: 입문부터 숙련까지!
Mar 25, 2024 pm 12:30 PM
GEMM(일반 행렬 곱셈)은 많은 응용 프로그램과 알고리즘의 중요한 부분이며 컴퓨터 하드웨어 성능을 평가하는 중요한 지표 중 하나이기도 합니다. GEMM 구현에 대한 심층적인 연구와 최적화는 고성능 컴퓨팅과 소프트웨어와 하드웨어 시스템 간의 관계를 더 잘 이해하는 데 도움이 될 수 있습니다. 컴퓨터 과학에서 GEMM의 효과적인 최적화는 컴퓨팅 속도를 높이고 리소스를 절약할 수 있으며, 이는 컴퓨터 시스템의 전반적인 성능을 향상시키는 데 중요합니다. GEMM의 작동 원리와 최적화 방법에 대한 심층적인 이해는 현대 컴퓨팅 하드웨어의 잠재력을 더 잘 활용하고 다양하고 복잡한 컴퓨팅 작업에 대한 보다 효율적인 솔루션을 제공하는 데 도움이 될 것입니다. GEMM의 성능을 최적화하여
 워드 문서에서 덧셈, 뺄셈, 곱셈, 나눗셈을 계산하는 방법
Mar 19, 2024 pm 08:13 PM
워드 문서에서 덧셈, 뺄셈, 곱셈, 나눗셈을 계산하는 방법
Mar 19, 2024 pm 08:13 PM
WORD는 워드를 사용하여 다양한 텍스트를 편집할 수 있는 강력한 워드 프로세서입니다. Excel 표에서는 덧셈, 뺄셈, 승수 계산 방법을 익혔습니다. 따라서 Word 표에서 숫자의 덧셈을 계산해야 한다면, 승수를 빼는 방법은 계산기로만 계산할 수 있나요? 대답은 물론 '아니요'입니다. WORD도 그렇게 할 수 있습니다. 오늘은 Word 문서에서 수식을 사용하여 표의 덧셈, 뺄셈, 곱셈, 나눗셈 등의 기본 연산을 계산하는 방법을 함께 배워보겠습니다. 그럼 오늘은 WORD 문서에서 덧셈, 뺄셈, 곱셈, 나눗셈을 계산하는 방법을 자세히 보여드리겠습니다. 1단계: WORD를 열고 툴바의 [삽입] 아래 [표]를 클릭한 후 드롭다운 메뉴에 표를 삽입합니다.
 Python의 count() 함수를 사용하여 목록의 요소 수를 계산하는 방법
Nov 18, 2023 pm 02:53 PM
Python의 count() 함수를 사용하여 목록의 요소 수를 계산하는 방법
Nov 18, 2023 pm 02:53 PM
Python의 count() 함수를 사용하여 목록의 요소 수를 계산하려면 특정 코드 예제가 필요합니다. 강력하고 배우기 쉬운 프로그래밍 언어인 Python은 다양한 데이터 구조를 처리하기 위한 많은 내장 함수를 제공합니다. 그 중 하나는 목록의 요소 수를 계산하는 데 사용할 수 있는 count() 함수입니다. 이번 글에서는 count() 함수의 사용법을 자세히 설명하고 구체적인 코드 예시를 제공하겠습니다. count() 함수는 Python의 내장 함수로, 특정 값을 계산하는 데 사용됩니다.
 행렬식을 사용하여 삼각형의 면적을 계산하는 Java 프로그램
Aug 31, 2023 am 10:17 AM
행렬식을 사용하여 삼각형의 면적을 계산하는 Java 프로그램
Aug 31, 2023 am 10:17 AM
소개 행렬식을 이용하여 삼각형의 면적을 계산하는 자바 프로그램은 세 꼭지점의 좌표를 주어 삼각형의 면적을 계산할 수 있는 간결하고 효율적인 프로그램이다. 이 프로그램은 Java에서 기본 산술 및 대수 계산을 사용하는 방법과 Scanner 클래스를 사용하여 사용자 입력을 읽는 방법을 보여주기 때문에 기하학을 배우거나 작업하는 모든 사람에게 유용합니다. 프로그램은 사용자에게 삼각형의 세 점 좌표를 묻는 메시지를 표시하고 이를 읽어 좌표 행렬의 행렬식을 계산하는 데 사용합니다. 행렬식의 절대값을 사용하여 면적이 항상 양수인지 확인한 다음 공식을 사용하여 삼각형의 면적을 계산하여 사용자에게 표시합니다. 이 프로그램은 다양한 형식의 입력을 받아들이거나 추가 계산을 수행하도록 쉽게 수정할 수 있으므로 기하학적 계산을 위한 다용도 도구가 됩니다. 행렬식의 순위
 Java에서 부분 문자열의 발생 횟수를 재귀적으로 계산합니다.
Sep 17, 2023 pm 07:49 PM
Java에서 부분 문자열의 발생 횟수를 재귀적으로 계산합니다.
Sep 17, 2023 pm 07:49 PM
두 개의 문자열 str_1과 str_2가 주어졌습니다. 목표는 재귀 프로시저를 사용하여 문자열 str1에서 하위 문자열 str2의 발생 횟수를 계산하는 것입니다. 재귀 함수는 정의 내에서 자신을 호출하는 함수입니다. str1이 "Iknowthatyouknowthatiknow"이고 str2가 "know"인 경우 발생 횟수는 -3입니다. 예를 들어 str1="TPisTPareTPamTP", str2="TP"를 입력하면 Countofoccurrencesofasubstringrecursi가 출력됩니다.
 C#에서 Math.Pow 함수를 사용하여 지정된 숫자의 거듭제곱을 계산하는 방법
Nov 18, 2023 am 11:32 AM
C#에서 Math.Pow 함수를 사용하여 지정된 숫자의 거듭제곱을 계산하는 방법
Nov 18, 2023 am 11:32 AM
C#에는 많은 수학 함수가 포함된 Math 클래스 라이브러리가 있습니다. 여기에는 지정된 숫자의 거듭제곱을 계산하는 데 도움이 되는 거듭제곱을 계산하는 Math.Pow 함수가 포함됩니다. Math.Pow 함수의 사용법은 매우 간단합니다. 밑수와 지수만 지정하면 됩니다. 구문은 다음과 같습니다. Math.Pow(base,expont); 여기서 base는 밑수를 나타내고 지수는 지수를 나타냅니다. 이 함수는 double형 결과, 즉 거듭제곱 계산 결과를 반환합니다. 하자
 행렬의 오른쪽 대각선 요소의 합을 계산하는 Python 프로그램
Aug 19, 2023 am 11:29 AM
행렬의 오른쪽 대각선 요소의 합을 계산하는 Python 프로그램
Aug 19, 2023 am 11:29 AM
널리 사용되는 범용 프로그래밍 언어는 Python입니다. 데스크톱 애플리케이션, 웹 개발, 기계 학습 등 다양한 산업에서 사용됩니다. 다행스럽게도 Python에는 초보자에게 적합한 간단하고 이해하기 쉬운 구문이 있습니다. 이 기사에서는 Python을 사용하여 행렬의 오른쪽 대각선의 합을 계산합니다. 매트릭스란 무엇입니까? 수학에서는 직사각형 배열이나 행렬을 사용하여 수학적 대상이나 그 속성을 설명합니다. 이는 행과 열로 배열된 숫자, 기호 또는 표현식을 포함하는 직사각형 배열 또는 테이블입니다. 예를 들어 -234512367574 따라서 3행 4열의 행렬이며 3*4 행렬로 표현됩니다. 이제 행렬에는 두 개의 대각선, 즉 주 대각선과 보조 대각선이 있습니다.
 총점과 백분율을 계산하는 Java 프로그램 예
Sep 11, 2023 pm 06:01 PM
총점과 백분율을 계산하는 Java 프로그램 예
Sep 11, 2023 pm 06:01 PM
Java 프로그램을 사용하여 총점과 백분율을 계산하는 방법을 보여 드리겠습니다. 총점은 사용 가능한 모든 점수의 합을 의미하며, 백분율은 계산된 점수를 총점으로 나누고 결과 숫자 100을 곱한 것을 의미합니다. Percent_of_marks=(obtained_marks/total_marks)×100 예제 1 총점과 백분율을 계산하는 방법을 보여주는 Java 프로그램입니다. //Totalmarks 및 Percentages가 어떻게 계산되는지 시연하는 JavaProgramimportjava.io.*;publicclassTotalMarks_




