양자 알고리즘은 새로운 종류의 문제를 해결합니다!

1994년에 한 수학자 한 사람이 일반 클래식 컴퓨터가 할 수 없는 일을 양자 컴퓨터로 수행하는 방법을 알아냈습니다. 이 작업은 원칙적으로 양자 역학의 규칙을 기반으로 하는 기계가 많은 수를 주요 요소로 효율적으로 분해할 수 있음을 보여줍니다. 이는 오늘날 인터넷 보안의 기본 요소 대부분을 구성하는 기존 컴퓨터에서는 매우 어려운 작업입니다.

그것과 함께 낙관주의의 물결이 옵니다. 아마도 연구자들은 우리가 수많은 다양한 문제를 해결할 수 있는 양자 알고리즘을 발명할 수 있을 것이라고 믿습니다.

하지만 진전이 멈췄습니다. Carnegie Mellon University의 Ryan O'Donnell은 "이것은 다소 실망스럽습니다"라고 말했습니다. "사람들은 '이건 훌륭합니다. 우리가 다른 모든 종류의 놀라운 알고리즘을 얻게 될 것이라고 확신합니다.'라고 말할 것입니다. 그렇지 않습니다." 과학자들은 NP라는 표준 세트에서 단일하고 좁은 문제 클래스에 대해서만 상당한 속도 향상을 발견했습니다. 이는 인수분해와 같은 효율적이고 검증 가능한 솔루션이 있음을 의미합니다.

지난 3년 동안 이런 일이 있었습니다. 그러다가 4월에 연구자들은 양자 컴퓨터가 기존 컴퓨터보다 더 빠르게 해결할 수 있는 완전히 새로운 종류의 문제를 발명했습니다. 여기에는 지저분한 출력만을 기반으로 복잡한 수학적 프로세스의 입력을 계산하는 작업이 포함됩니다. 이 문제가 단독으로 발생하는지 아니면 다른 많은 문제 중 첫 번째 문제인지는 아직 결정되지 않았습니다.

MIT의 컴퓨터 과학자인 Vinod Vaikuntanathan은 "많은 사람들이 세상에 또 무엇이 있을지 생각하고 있습니다."라고 말합니다. 양자 컴퓨터가 더 잘하는 것이 무엇인지 이해하기 위해 수학적 모델을 연구하여 이를 표현합니다. 일반적으로 그들은 오라클이라는 이상적인 컴퓨터와 쌍을 이루는 양자 또는 고전 컴퓨터 모델을 상상합니다. 오라클은 입력을 받아 미리 결정된 출력을 출력하는 간단한 수학 함수 또는 컴퓨터 프로그램과 같습니다.

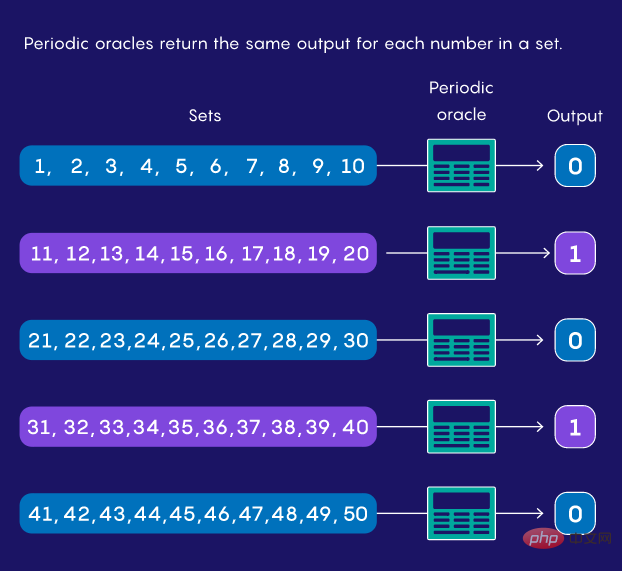
입력이 임의의 범위(예: 12~67) 내에 있으면 "yes"를 출력하고 그렇지 않으면 "no"를 출력하는 임의의 동작이 있을 수 있습니다. 또는 주기적일 수 있으므로 1~10 사이의 입력은 "예"를 반환하고, 11~20은 "아니요"를 반환하고, 21~30은 다시 "예"를 반환하는 식으로 계속됩니다.

주기적인 예언 중 하나가 있지만 그 기간을 모른다고 가정해 보세요. 당신이 할 수 있는 일은 숫자를 입력하고 출력 내용을 확인하는 것뿐입니다. 이러한 제약 하에서 컴퓨터는 얼마나 빨리 주기를 찾을 수 있습니까? 1993년 당시 몬트리올 대학교의 다니엘 사이먼(Daniel Simon)은 양자 알고리즘이 어떤 기존 알고리즘보다 밀접하게 관련된 문제에 대한 답을 더 빠르게 계산할 수 있음을 발견했습니다.

이 결과를 통해 Simon은 양자 컴퓨터가 중요한 이점을 갖는 첫 번째 징후 중 하나를 식별할 수 있습니다. 그러나 그가 주요 학회에 논문을 제출했을 때 거절당했습니다. 그러나 그 논문은 당시 뉴저지의 벨 연구소에서 일하고 있던 컨퍼런스 프로그램 위원회의 하급 위원인 피터 쇼어(Peter Shor)의 관심을 불러일으켰습니다.

Shor는 계속해서 Simon의 알고리즘을 조정하여 오라클의 기간을 계산할 수 있다는 사실을 발견했습니다. 그런 다음 그는 주기적인 예언처럼 동작하는 방정식, 즉 주기적인 인수분해를 설명하는 방정식을 풀기 위해 알고리즘을 다시 조정할 수 있다는 것을 깨달았습니다.

Shor의 결과는 역사적이었습니다. 그가 발견한 양자 알고리즘은 거대한 숫자를 구성 소인수로 빠르게 줄일 수 있는데, 이는 알려진 기존 알고리즘으로는 할 수 없는 일입니다. 이후 몇 년 동안 연구자들은 다른 효율적인 양자 알고리즘을 발견했습니다. Shor의 알고리즘과 같은 일부는 지수적 이점을 제공하기까지 했지만 비주기적 NP 문제에 대해서는 어느 누구도 상당한 양자 이점을 증명할 수 없었습니다.

진행이 부족하여 오스틴에 있는 텍사스 대학의 Scott Aaronson과 라트비아 대학의 Andris Ambainis라는 두 명의 컴퓨터 과학자가 관찰을 했습니다. 양자 이점의 증명은 항상 주기성과 같은 일부 비무작위 구조를 사용한 예측에 의존하는 것 같습니다. 2009년에는 무작위 또는 구조화되지 않은 NP 문제에 대해 속도가 크게 향상되지 않을 것이라고 추측했으며 누구도 예외를 찾을 수 없었습니다.

그들의 추측은 양자 컴퓨터의 성능을 제한합니다. 그러나 특정 유형의 구조화되지 않은 NP 문제(예 또는 아니요 답변이 있는 문제)의 경우 속도가 크게 향상되지 않는다고 말할 뿐입니다. 문제가 소위 검색 문제라고 하는 보다 구체적이고 정량적인 답을 찾는 것과 관련된 경우에는 이 추측이 적용되지 않습니다.

이를 염두에 두고 NTT 사회 정보학 연구소의 Takashi Yamakawa 연구원과 NTT Research 및 Princeton University의 Mark Zhandry 연구원은 2005년 Oded Regev가 제기한 특정 검색 문제를 실험하기로 결정했습니다.

풍향계 세트가 모두 같은 방향을 향하고 있다고 상상해 보세요. 그들 각각에게 신중한 힘을 주고 돌풍이 그들의 방향에 영향을 미치게 하십시오. Regev는 최종 방향을 기반으로 원래 가리킨 위치를 확인하려고 합니다. 이와 같은 문제는 추력과 바람이 원래 방향에서 무작위 오류 소스로 작용하기 때문에 "오류 학습"으로 알려지게 되었습니다. 고전 알고리즘과 양자 알고리즘 모두 해결하기 어렵다는 증거가 있습니다.

Yamakawa와 Zhandry가 설정을 조정했습니다. 그들은 이러한 시작의 힘을 수정하여 더 예측 가능하게 만들었습니다. 그들은 또한 무작위 오라클에 의해 바람을 결정하도록 만들었기 때문에 어떤 경우에는 훨씬 더 무작위이지만 다른 경우에는 완전히 휴면 상태입니다.

이러한 수정을 통해 연구원들은 양자 알고리즘이 초기 방향을 효과적으로 찾을 수 있음을 발견했습니다. 그들은 또한 모든 기존 알고리즘이 지수 요인에 의해 속도가 느려져야 함을 증명했습니다. Shor와 마찬가지로 그들은 알고리즘을 적용하여 문제의 현실적인 버전을 해결하고 예측을 실제 수학 방정식으로 대체했습니다.

컴퓨터 과학자들은 여전히 ​​이 문제를 이해하고 해결하려고 노력하고 있습니다. Vaikuntanathan은 이를 데이터 압축을 수행할 때 발생하는 다른 상황과 비교했습니다. 즉, 정보가 압축되면 두 비트가 실수로 같은 위치에 압착되어 덮어쓰게 될 수 있습니다. 이러한 충돌을 피하기 위해 사전에 이러한 충돌을 예측하는 문제에는 몇 가지 유사점이 있습니다. 그는 "이것은 기본적으로 이런 문제 종류입니다. 아마도 이러한 문제는 양자적으로 해결될 수 있을 것입니다."라고 말했습니다. "아마도 오늘날의 초기 버전의 양자 컴퓨터에서도 새로운 문제와 같은 구조화되지 않은 문제도 해결될 수 있기를 바랍니다." 해결하여 테스트할 수 있는 방법을 제공합니다. 구조화되지 않은 문제는 이미 무작위이기 때문에 프로그래밍하는 데 더 적은 리소스가 필요하거나 노이즈에 덜 민감할 수 있다는 아이디어였습니다. 그러나 지금까지 이 새로운 문제는 기존 양자 컴퓨터가 해결하기에는 너무 발전된 것으로 보입니다. Aaronson은 "이것은 이상한 문제입니다. 나는 그것을 정의할 생각은 하지 않았지만 돌이켜보면 NP 기반 문제에 대한 중요한 양자적 이점의 몇 가지 예를 가지고 있습니다"라고 말했습니다. 양자 세계의 다른 많은 문제들이 거의 해결 불가능한 문제에서 해결 가능한 문제로 바뀔까요? 이제 그렇게 생각하는 데에는 더 많은 이유가 있습니다. O'Donnell은 "이것은 양자 컴퓨터가 어떤 문제를 잘 해결하는지에 대한 우리의 견해를 어느 정도 변화시킵니다."라고 말했습니다.

위 내용은 양자 알고리즘은 새로운 종류의 문제를 해결합니다!의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!