사용자 정의 클래스를 사용하여 Java에서 배열을 캡슐화하여 데이터 작업을 구현하는 방법

기본적인 데이터 저장 구조로는 어레이가 널리 사용됩니다. 배열은 연속적인 메모리 공간을 사용하여 고정 길이와 동일한 데이터 유형을 저장하는 데이터 구조입니다. 데이터 구조는 언어 독립적입니다. 여기서 Java는 배열 관련 작업을 수행하는 데 사용됩니다. 배열 인덱스는 0부터 시작합니다.

1 배열 초기화

데이터를 생성하는 방법에는 두 가지가 있습니다. 하나는 고정된 길이의 데이터를 선언한 후 배열에 값을 할당하는 것이고, 다른 하나는 직접 값을 할당하는 것입니다.

유형 1:

数据类型[] 数组名称 = new 数据类型[长度];

여기에서 [] 표시는 배열을 선언합니다. 이 []는 데이터 유형 뒤에 배치될 수도 있으며 배열 명사 뒤에 배치할 수도 있습니다. 길이가 2인 long 유형의 배열을 선언하고 값을 할당하면: 2的long类型的数组，并赋值：

long[] arr = new long[2];
arr[0] = 1;
arr[1] = 2;

第二种：

数据类型[] 数组名称 = {元素1,元素2, ...};

这样在数组初始化的时候直接给数组赋值，数组的长度由元素的个数决定。

二 自定义类封装数组实现数据操作

public class MyArray {

    // 自定义数组    private long[] arr;
    // 有效数据长度    private int element;

    public MyArray(){
        arr = new long[9];
    }

    public MyArray(int maxsize){
        arr = new long[maxsize];
    }
    /**
     * 显示数组元素
     */    public void display(){
        System.out.print("[");
        for (int i = 0; i < element; i++) {
            System.out.print(arr[i]+" ");
        }
        System.out.print("]");
    }
}

2.1 添加元素

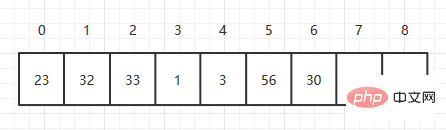
数组是用连续的内存空间来存储数据的，则每次添加的时候会往当前数组的最后一个元素上添加元素，一次就可以加上元素，所以它的复杂度为O(1)，假如定义一个长度为9数组，数组中已经有两个元素，则添加第三个元素如下：

public void add(long value){
    arr[element] = value;
    element++;
}

2.2 根据值查询元素位置

这种查找方式也叫做线性查找，就是根据传入的值循环去遍历元素，来获取对应的位置，理论上平均查询一个元素需要花费N/2次，所以它的复杂度为O(N)。

public int find(long value){
    int i;
    for (i = 0; i < element; i++) {
        if(value == arr[i]){
            break;
        }
    }
    if(i == element){
        return -1;
    }else {
        return i;
    }
}

2.3 根据索引查询元素

根据索引来查找元素，也就是获取对应位置的元素，其复杂度为O(1)。

public long get(int index){
    if(index >= element || index < 0){
        throw new ArrayIndexOutOfBoundsException();
    }else {
        return arr[index];
    }
}

2.4 根据索引删除元素

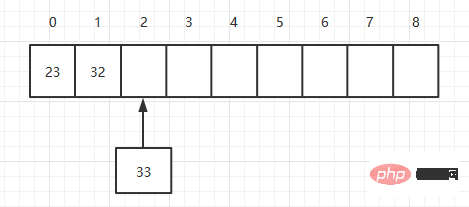
删除对应索引的元素后，我们需要将所有改索引后面的元素，向前移动一位。假如我要删除索引为2的元素，如下：

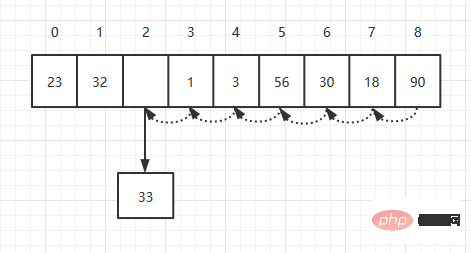
理论上平均删除一个元素，我们需要移动N/2次，所以它的时间复杂度也为O(N)。

public void delete(int index){
    if(index >= element || index < 0){
        throw new ArrayIndexOutOfBoundsException();
    }else {
        for (int i = index; i < element; i++) {
            arr[index] = arr[index+1];
        }
        element --;
    }
}

2.5 修改元素

修改某个位置的元素，直接根据索引就一次就可以修改对应的元素，所以它的时间复杂度为O(1)。

public void change(int index,long newValue){
    if(index >= element || index < 0){
        throw new ArrayIndexOutOfBoundsException();
    }else {
        arr[index] = newValue;
    }
}

三 有序数组

有序数组是数组的一种特殊类型，有序数组中的元素按照某种顺序进行排列。

3.1 添加元素

在添加元素的时候，将元素按顺序添加到某个位置。如下，在一个数组中添加一个33的元素。

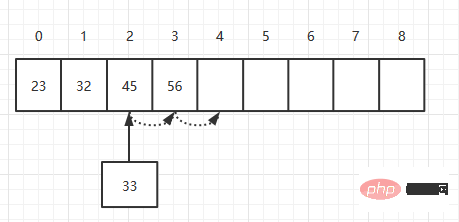
首先，将索引为3的元素移动到索引为4的位置，然后将索引为2的元素移动到索引为3的位置，最后将33添加到索引为2的位置。理论上插入一个元素需要移动元素的个数为N/2个，所以它的时间复杂度为O(N)。

public void add(long value){
    int i;
    for (i = 0; i < element; i++) {
        if(arr[i]>value){
            break;
        }
    }

    for (int j = element; j > i; j--){
        arr[j] = arr[j-1];
    }
    arr[i] = value;
    element++;
}

3.2 二分法根据元素查询索引

在无序数组中，使用线性法进行查找相关元素，线性法即按索引按个查找。有序数组可以使用二分法来查找元素，二分法是指将一个数组从中间分成两个，判断元素位于哪个数组中，然后重复这样的操作。

假如有8

public int search(long value){
    // 中间值    int middle = 0;
    // 最小值    int low = 0;
    // 最大值    int pow = element;
    while (true){
        middle = (low + pow) / 2;
        if(arr[middle] == value){
            return middle;
        }else if (low > pow){
            return -1;
        }else{
            if(arr[middle] > value){
                pow = middle - 1;
            }else{
                low = middle + 1;
            }
        }
    }
}

두 번째 종류

:

rrreee

이렇게 하면 배열이 초기화되면 배열 할당이 직접 주어지며 배열의 길이는 요소 수에 따라 결정됩니다. 두 개의 사용자 정의 클래스가 배열을 캡슐화하여 데이터 작업을 구현합니다.rrreeerrreee2.2 값에 따른 요소 위치 쿼리이 검색 방법이라고도 합니다. 선형 검색은 들어오는 값에 따라 요소를 반복하여 해당 위치를 얻는 것입니다. 이론적으로 요소를 쿼리하는 데 평균 N/2번이 걸리므로 복잡도는 O(N)입니다. 2.3 인덱스 기반 요소 쿼리 인덱스 기반 요소 찾기, 즉 해당 위치의 요소를 가져오는 방식으로 복잡도는 O(1)입니다. rrreee2.4 인덱스를 기준으로 요소 삭제 인덱스에 해당하는 요소를 삭제한 후 인덱스 뒤의 모든 요소를 ​​한 위치 앞으로 이동해야 합니다. 인덱스 2가 있는 요소를 삭제하려면 다음과 같이 하세요. 이론적으로 평균 요소를 삭제하려면 N/2번 이동해야 하므로 시간 복잡도도 O(N)입니다. 2.5 요소 수정 특정 위치의 요소를 수정하고 해당 요소를 인덱스에 따라 직접 한 번 수정하므로 시간 복잡도는 O(1)입니다. rrreee3개의 순서 배열순서 배열은 배열의 특별한 유형입니다. 순서 배열의 요소는 특정 순서로 배열됩니다. 3.1 요소 추가요소 추가 시 특정 위치에 순서대로 요소를 추가하세요. 다음과 같이 33 요소를 배열에 추가합니다. 먼저 인덱스 3인 요소를 인덱스 4인 위치로 이동하고, 그런 다음 인덱스 2의 요소를 인덱스 3의 위치로 이동하고 마지막으로 인덱스 2의 위치에 33을 추가합니다. 이론적으로 요소를 삽입하려면 N/2개의 요소를 이동해야 하므로 시간 복잡도는 O(N)입니다. rrreee3.2 요소를 기준으로 인덱스를 쿼리하는 이분법순서가 지정되지 않은 배열에서 관련 요소를 찾는 선형 방법은 인덱스를 기준으로 하나씩 검색하는 것입니다. 정렬된 배열은 이분법(dichotomy) 방법을 사용하여 요소를 찾을 수 있습니다. 이분법이란 배열을 가운데에서 두 개로 나누고 해당 요소가 어떤 배열에 있는지 확인한 다음 이 작업을 반복하는 것을 의미합니다. 8 요소가 있는 배열이 있다고 가정합니다. 배열의 내용은 0-7의 순서대로 배열되어 있습니다. 요소 5를 찾으려면 0-3과 4-의 두 배열로 나뉩니다. 7을 처음으로 배열한 다음 4-7을 두 개의 배열 4-5와 6-7로 나누고 마지막으로 4-5를 4와 5로 나누어서 특정 요소를 쿼리할 수 있습니다. 길이가 8인 배열을 쿼리합니다. 특정 요소에 대한 복잡도는 O(logN)입니다(컴퓨터에서 logN의 밑수는 일반적으로 2를 나타내며, 이는 2의 거듭제곱이 n과 같음을 의미). rrreeeIV 요약

2.1 요소 추가	배열은 연속 메모리 공간을 사용하여 데이터를 저장하므로 요소를 추가할 때마다 요소가 현재 배열의 마지막 요소에 추가됩니다. 요소를 추가할 수 있으므로 복잡성은 O(1)입니다. 길이가 9인 배열을 정의하고 배열에 이미 두 개의 요소가 있는 경우 다음과 같이 세 번째 요소를 추가하세요.
rrreee
rrreee

복잡도가 낮을수록 알고리즘이 더 좋아집니다. 따라서 O(1) > O(logN) > O(N) >
2. 알고리즘
   복잡성

🎜🎜🎜🎜선형 검색🎜🎜O(N)🎜🎜🎜🎜이진 검색🎜🎜O(logN)🎜🎜🎜 🎜순서가 지정되지 않은 숫자 그룹 삽입 🎜🎜O(1 )🎜 🎜🎜🎜순서 있는 배열 삽입🎜🎜O(N)🎜🎜🎜🎜순서 없는 배열 삭제🎜🎜O(N)🎜🎜🎜🎜순서 있는 배열 삭제🎜🎜O(N)🎜🎜🎜🎜🎜 🎜 🎜 순서가 지정되지 않은 배열 삽입이 빠릅니다. , 검색 및 삭제가 느림🎜🎜🎜🎜순서 배열 검색이 빠르고, 삽입 및 삭제가 느림🎜🎜🎜

위 내용은 사용자 정의 클래스를 사용하여 Java에서 배열을 캡슐화하여 데이터 작업을 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!