Python에서 arctan 변환 각도를 구현하는 방법

직교 좌표계

평면 좌표계의 경우 광선 OP와 x축 사이의 각도 θ의 범위는 [0,2π) 또는 (-π,&pi일 수 있습니다. ;] 달리 지정하지 않는 한 후자를 사용하여
직교 공간 좌표계의 점 Pc = (x, y, z)를 구면 좌표계의 형태로 표현합니다Ps = ( θ , ф , r ) θ的范围，可以取[0,2π)或者(-π,π]，如无特殊说明， 我们统一使用后者。
将笛卡尔空间坐标系中的点 Pc = ( x , y , z ) 表示成球体坐标系中的形式 Ps = ( θ , ϕ , r )。

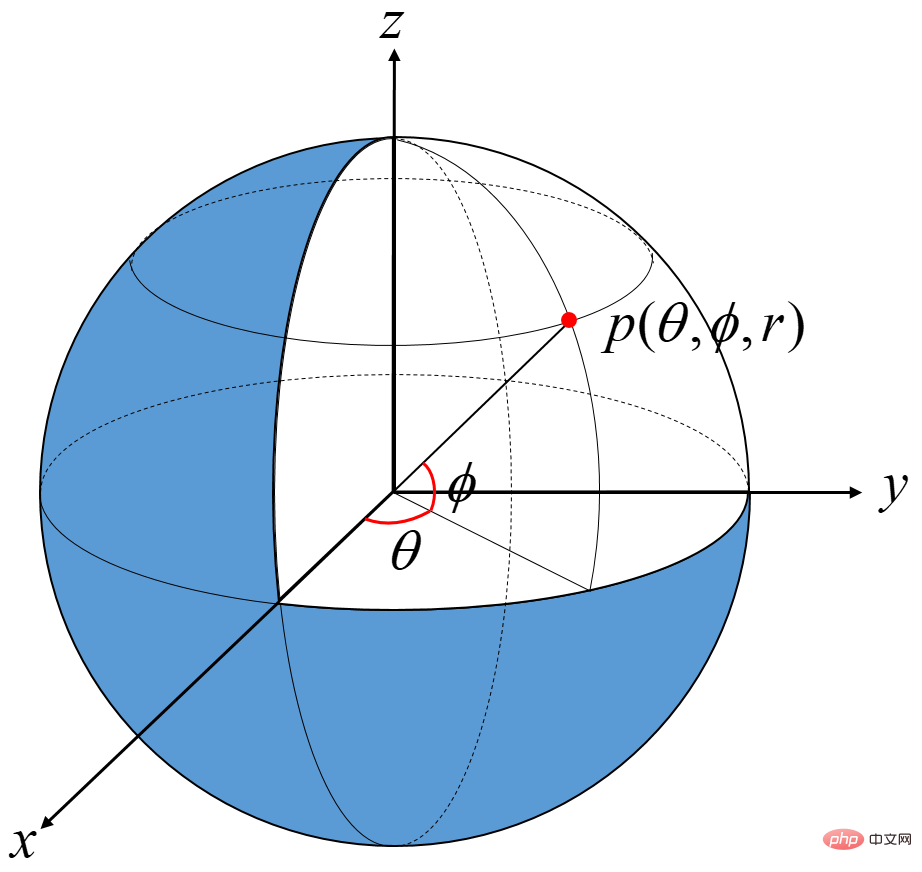
其中

根据球坐标的定义，要求θ∈[−π,π]，ϕ∈[−π/2,π/2] ，r∈[0 , +∞)。

对于 θ，正切函数的周期是 π，因此反正切函数 arctan 一般也只取一个周期，其定义域是 R，值域是(−π/2 , π/2) 。为了解决这个问题，引入了 Arctan 函数，也就是 arctan2 函数。

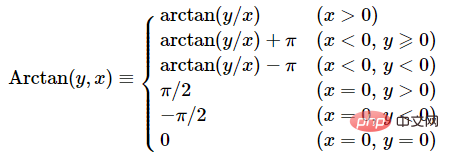
atan2 函数的使用 atan2(delta_y , delta_x)

import math
a = math.atan2(400,-692.820)
# 2.6179936760992044
angle = a/math.pi*180
# 149.99998843242386

atan 函数的使用 atan(delta_y / delta_x)

import math
delta_y = 400
delta_x = -692.820

if delta_x == 0:
    b = math.pi / 2.0
    angle = b/math.pi*180
    if delta_y == 0:
        angle = 0.0
    elif delta_y < 0:
        angle -= 180
else:
    b =  math.atan(delta_y/delta_x) 
    angle = b/math.pi*180
    if delta_y > 0 and delta_x < 0:
        angle = angle + 180
    if delta_y < 0 and delta_x < 0:
        angle = angle - 180

b,angle
# (-0.5235989774905888, 149.99998843242386)

atan 和 atan2 的异同

• 参数的个数不同

• 两者返回值都是弧度

• 如果 delta_x等于0，atan2依然可以计算，但是 atan 则需要提前判断，否则就会导致程序出错

• 象限的处理

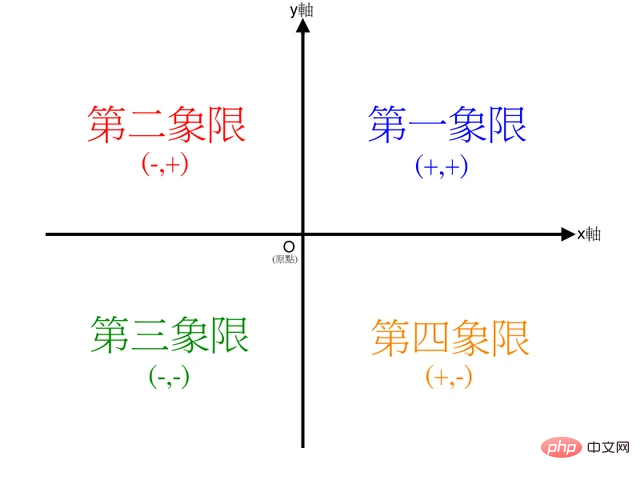
atan2(b,a)是4象限反正切，它的取值不仅取决于正切值b/a，还取决于点(b,a) 落入哪个象限：

• 当点 (b,a) 落入第一象限(b>0, a>0)时，atan2(b,a)的范围是 0 ~ pi/2

• 当点 (b,a)落入第二象限(b>0, a<0)时，atan2(b,a)的范围是 pi/2 ~ pi

• 当点 (b,a)落入第三象限(b<0, a<0)时，atan2(b,a)的范围是 -pi～-pi/2

• 当点 (b,a) 落入第四象限(b<0, a>0)时，atan2(b,a)的范围是 -pi/2～０

而 atan(b/a) 仅仅根据正切值为a/b求出对应的角度 (可以看作仅仅是2象限反正切)：

• 当 b/a > 0 时，atan(b/a)取值范围是 0 ~ pi/2

• 当 b/a < 0 时，atan(b/a)取值范围是 -pi/2～0

取值范围

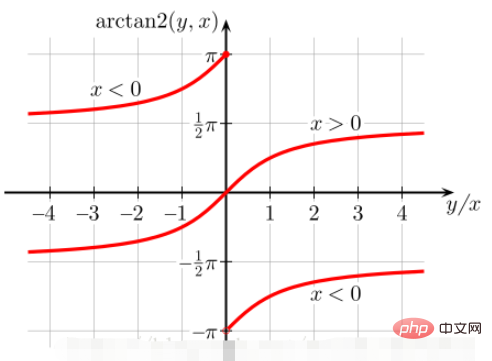
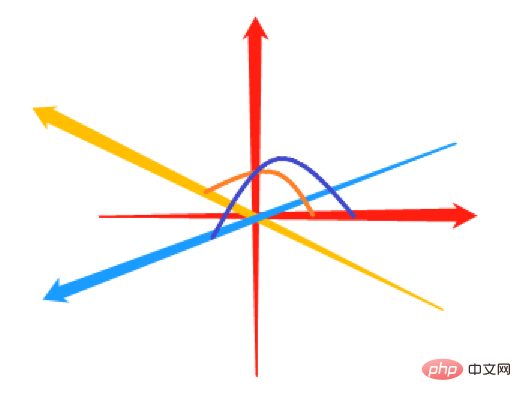
• 点 (b,a) 落入第一象限 (b>0, a>0)或 <code>第四象限(b<0, a>0)时，atan2(b,a) = atan(b/a)

• 点 (b,a) 落入第二象限 (b>0, a<0)，b/a<0，故atan(b/a)取值范围始终是 -pi/2～０，然而，atan2(b,a)的范围是 pi/2 ~ pi，故atan(b/a) 计算角度值要加180。

• 点 (b,a) 落入第三象限(b<0, a<0) ，b/a>0，故 atan(b/a) 取值范围是 0 ~ pi/2，而此时atan2(b,a)的范围是 -pi～-pi/2

그 중

🎜🎜구면좌표의 정의에 따르면, θ∈[−π,π], ф∈[−π/2,π/2], r∈[0, +∞). 🎜🎜 θ의 경우 탄젠트 함수의 주기는 π이므로 아크탄젠트 함수 arctan은 일반적으로 한 주기만 취하고 도메인은 R이며 값 범위는 (#minus;π/ 2, ∅/2). 이 문제를 해결하기 위해 arctan2 함수라고도 알려진 Arctan 함수가 도입되었습니다. 🎜🎜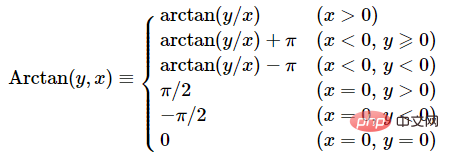🎜🎜atan2 함수 사용법 atan2(delta_y, delta_x)🎜rrreee🎜atan 함수 사용 atan(delta_y / delta_x)🎜rrreee🎜atan과 atan2의 유사점과 차이점🎜

• 🎜매개변수 개수가 다릅니다🎜🎜
• 🎜반환값 ​​둘 다 동일한 라디안🎜🎜
• 🎜delta_x가 0이면 atan2를 계산할 수 있지만 atan을 미리 판단해야 합니다. 그렇지 않으면 프로그램 오류가 발생합니다🎜🎜
• 🎜사분면 처리🎜🎜 🎜🎜🎜🎜atan2(b,a)는 4사분면 아크 탄젠트입니다. 값은 접선 값 b/a에 따라 달라질 뿐만 아니라 점 (b, a)가 어느 사분면에 속하는지에 따라 달라집니다. 🎜
  • 🎜점 (b, a) 첫 번째 사분면(b>0, a>0)에 속하며 atan2(b,a)의 범위는 0 ~ pi/2🎜🎜
  • 🎜점(b, a)가 두 번째 사분면(b>0, api/2 ~ pi🎜🎜
  • 🎜점(b, a) 제3사분면(b-pi~-pi/2🎜🎜
  • 🎜점( b,a)는 제4사분면(b0)에 속하며 atan2(b,a)의 범위는 -pi/2~0🎜🎜🎜🎜이고 atan(b /a)는 a/b의 탄젠트 값만을 기준으로 계산됩니다. 해당 각도(2 사분면의 아크 탄젠트로 간주될 수 있음): 🎜
    • 🎜 b/a > 0일 때 atan(b/a)의 값 범위는 0 ~ pi/2🎜🎜
    • 🎜b/a < atan(b/a)는 -pi/2~0🎜🎜🎜🎜값 범위🎜🎜🎜🎜🎜
      • 🎜점 (b,a)는 < When code>첫 번째 사분면(b>0, a>0) 또는 네 번째 사분면(b<0, a>)에 속합니다. ;0), atan2(b,a) = atan(b/a) 🎜🎜
      • 🎜점 (b,a)는 제2사분면(b> 0, a, b/a-pi/2~0입니다. atan2(b,a)는 <code>pi/2 ~ pi이므로 atan(b/a)에서 계산한 각도 값에 180을 더해야 합니다. 🎜🎜
      • 🎜점 (b,a)는 3사분면(b, b/a>0에 속하므로 atan(b/a의 값 범위는 )는 <code>0 ~ pi/2이고 이때 atan2(b,a)의 범위는 -pi~-pi/2이므로 atan(b/a ) 각도를 계산합니다. 값이 180만큼 감소합니다. 🎜🎜🎜🎜결론: atan과 atan2 함수는 atan2 함수를 사용하는 것이 좋습니다🎜

  위 내용은 Python에서 arctan 변환 각도를 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!