분할 정복 알고리즘을 배우기 전에 한 가지 질문을 드리겠습니다. 어릴 때 저금통을 보신 경험이 있으실 거라 생각합니다. 우리 모두는 돈을 세어 볼 때가 있을 것입니다. 하지만 데이터는 두뇌에 비해 크기가 크고 실수하기 쉽기 때문에 돈 더미를 처리하는 것이 복잡하다고 생각할 수 있습니다. . 이 돈더미의 총액
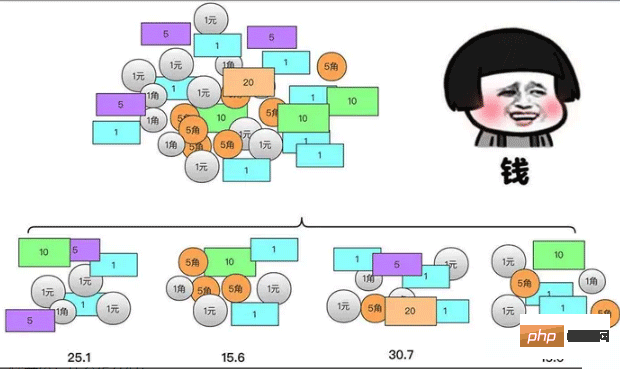
물론, 각 부분의 돈이 아직 너무 크다고 생각된다면, 나누어서 합칠 수도 있습니다.
작은 돈더미 하나하나 계산 방법은 가장 큰 돈더미를 계산하는 방법과 동일합니다(차이는 크기에 있음)
그러면 큰 더미의 돈더미의 합은 실제로는 작은 돈 더미의 결과. 이런 식으로 실제로 분열과 정복 사고 방식이 있습니다.
분할 정복 알고리즘은 분할 정복이란 개념을 이용한 알고리즘입니다.
분할 및 정복, 문자 그대로 설명은 "분할 및 정복"입니다. 이는 복잡한 문제를 두 개 이상의 동일하거나 유사한 하위 문제로 나눈 다음 하위 문제를 더 작은 하위 문제로 나누는 것입니다... 하위 문제는 간단하고 직접적으로 해결될 수 있으며, 원래 문제에 대한 해결책은 하위 문제에 대한 솔루션의 조합입니다. 컴퓨터 과학에서 분할정복법은 분할정복 개념을 활용한 매우 중요한 알고리즘이다. 분할 정복 방법은 정렬 알고리즘(빠른 정렬, 병합 정렬), 푸리에 변환(빠른 푸리에 변환) 등과 같은 많은 효율적인 알고리즘의 기초입니다.
부모 문제를 하위 문제로 분해하고 동일한 방식으로 해결합니다. 이는 재귀 개념과 일치하므로 분할 정복 알고리즘은 일반적으로 재귀적인 방식으로 구현됩니다. 재귀 구현).
분할 정복 알고리즘에 대한 설명은 문자 그대로 이해하기 쉽습니다. 분할 정복에는 실제로 병합 프로세스가 포함됩니다.
분할: 더 작은 문제를 재귀적으로 해결합니다(종료 레이어로 또는 가능한 경우 중지). 해결하세요)
정복: 문제가 충분히 작으면 직접 해결하세요.
결합: 하위 문제의 해를 상위 클래스 문제로 구성합니다.
일반적인 분할 정복 알고리즘은 텍스트에서 두 개 이상의 재귀 호출과 하위 클래스 문제로 분해됩니다. 일반적으로 제출을 원하지 않습니다(서로 영향을 주지 않음). 매우 크고 직접적으로 해결하기 어려운 문제를 해결하는 경우, 크기가 작아서 해결하기 쉽고 문제가 분할 정복 알고리즘의 적용 조건을 충족하는 경우 분할 정복 알고리즘을 사용할 수 있습니다. .
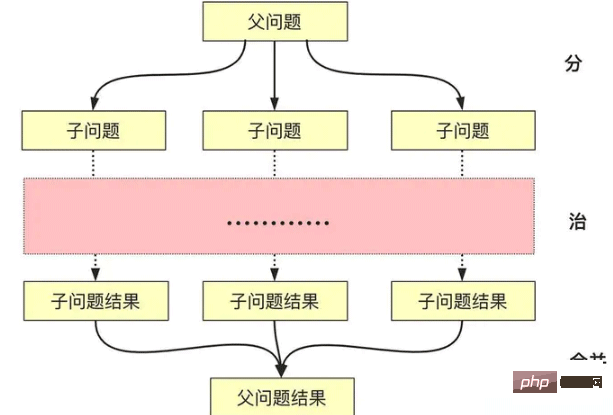
그러면 분할정복 알고리즘으로 문제를 해결하려면 어떤 조건(특성)을 충족해야 할까요?
1. 원래 문제는 대개 규모가 커서 직접 해결하기 어렵습니다. 그러나 문제는 어느 정도 줄어들면 더 쉽게 해결될 수 있습니다.
2. 문제는 동일한(유사한) 해결 방법을 사용하여 여러 개의 작은 하위 문제로 분해될 수 있습니다. 그리고 하위 문제에 대한 해결책은 독립적이며 서로 영향을 미치지 않습니다.
3. 문제 분해의 하위 문제를 병합하여 문제에 대한 해결책을 얻을 수 있습니다.
분할정복 알고리즘과 재귀의 관계가 무엇인지 궁금하신가요? 실제로 분할정복은 문제를 분할하고 정복하고 합치는 과정에 초점을 맞춘 중요한 사고이다. 재귀(Recursion)는 자신을 호출하는 메서드를 사용해 앞뒤로 진행되는 과정을 형성하는 방법(도구)이며, 분할 정복은 이러한 앞뒤 과정을 여러 개 활용할 수 있습니다.
분할 정복 알고리즘의 경우 중요한 것은 그 아이디어입니다. 우리는 이를 구현하기 위해 주로 재귀를 사용하기 때문에 대부분의 코드 구현은 매우 간단합니다. 그리고 이 글 역시 생각을 말하는 데 중점을 두고 있습니다.
분할 정복 알고리즘의 고전적인 문제는 두 가지 범주로 나뉩니다. 하위 문제는 완전히 독립적이고 하위 문제는 완전히 독립적이지 않습니다.
1. 하위 문제는 완전히 독립적입니다. 즉, 원래 질문에 대한 답은 하위 문제의 결과에서 완전히 도출될 수 있습니다.
2. 하위 문제는 완전히 독립적이지 않습니다. 일부 간격 문제 또는 교차 간격 문제는 분할 및 정복을 사용하여 문제를 고려할 때 주의 깊게 학습해야 합니다.
이진 검색은 분할 정복의 예이지만 이진 검색에는 고유한 특성이 있습니다
순서가 정렬됩니다
결과는 값입니다
검색은 완전한 간격을 두 개의 간격으로 나누어서 따로 값을 찾은 후 결과를 확인해야 합니다. 그러나 정렬된 간격을 통해 결과가 어느 간격에 있는지 직접 확인할 수 있으므로 나누어진 두 개의 간격만 필요합니다. 간격 중 하나를 계산한 다음 끝까지 계속합니다. 재귀적 구현과 비재귀적 구현이 있지만 비재귀적 구현이 더 일반적으로 사용됩니다.
public int searchInsert(int[] nums, int target) {
if(nums[0]>=target)return 0;//剪枝
if(nums[nums.length-1]==target)return nums.length-1;//剪枝
if(nums[nums.length-1]<target)return nums.length;
int left=0,right=nums.length-1;
while (left<right) {
int mid=(left+right)/2;
if(nums[mid]==target)
return mid;
else if (nums[mid]>target) {
right=mid;
}
else {
left=mid+1;
}
}
return left;
}빠른 정렬도 분할 정복의 예입니다. 빠른 정렬의 각 패스는 숫자를 선택하고 이 숫자보다 작은 숫자를 왼쪽에 배치하고 오른쪽에 이 숫자보다 큰 숫자를 배치합니다. , 그리고 문제를 해결하기 위해 재귀적으로 분할하고 정복합니다. 물론 두 하위 범위의 경우 분할할 때 빠른 정렬이 많은 작업을 수행했습니다. 모두 하위 수준으로 정렬되면 이 시퀀스의 값이 정렬된 값입니다. . 이는 분열과 정복의 표현이다.
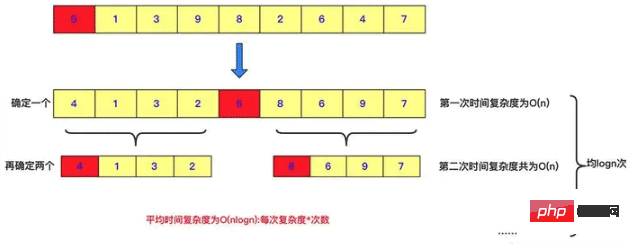
public void quicksort(int [] a,int left,int right)
{
int low=left;
int high=right;
//下面两句的顺序一定不能混,否则会产生数组越界!!!very important!!!
if(low>high)//作为判断是否截止条件
return;
int k=a[low];//额外空间k,取最左侧的一个作为衡量,最后要求左侧都比它小,右侧都比它大。
while(low<high)//这一轮要求把左侧小于a[low],右侧大于a[low]。
{
while(low<high&&a[high]>=k)//右侧找到第一个小于k的停止
{
high--;
}
//这样就找到第一个比它小的了
a[low]=a[high];//放到low位置
while(low<high&&a[low]<=k)//在low往右找到第一个大于k的,放到右侧a[high]位置
{
low++;
}
a[high]=a[low];
}
a[low]=k;//赋值然后左右递归分治求之
quicksort(a, left, low-1);
quicksort(a, low+1, right);
}퀵 정렬은 분할할 때 많은 작업을 하는데, 병합은 그 반대인데, 병합할 때는 양에 따라 균등하게 분할합니다. 2x2 순서대로 병합합니다. 왜냐하면 두 개의 정렬된 시퀀스의 O(n) 수준 복잡성으로 필요한 결과를 얻을 수 있기 때문입니다. 병합 정렬을 기반으로 한 역순수의 변형도 분할 정복 아이디어로 해결됩니다.
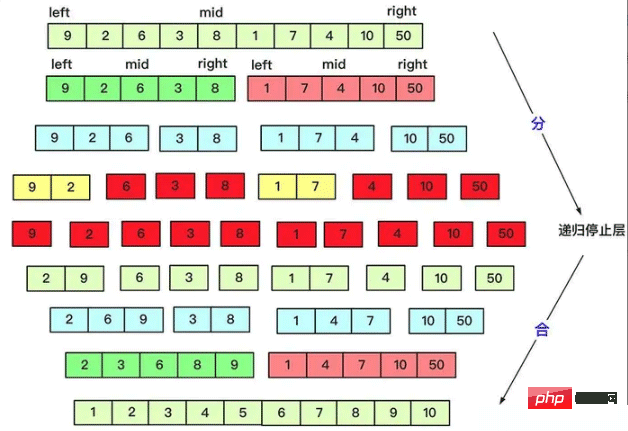
private static void mergesort(int[] array, int left, int right) {
int mid=(left+right)/2;
if(left<right)
{
mergesort(array, left, mid);
mergesort(array, mid+1, right);
merge(array, left,mid, right);
}
}
private static void merge(int[] array, int l, int mid, int r) {
int lindex=l;int rindex=mid+1;
int team[]=new int[r-l+1];
int teamindex=0;
while (lindex<=mid&&rindex<=r) {//先左右比较合并
if(array[lindex]<=array[rindex])
{
team[teamindex++]=array[lindex++];
}
else {
team[teamindex++]=array[rindex++];
}
}
while(lindex<=mid)//当一个越界后剩余按序列添加即可
{
team[teamindex++]=array[lindex++];
}
while(rindex<=r)
{
team[teamindex++]=array[rindex++];
}
for(int i=0;i<teamindex;i++)
{
array[l+i]=team[i];
}
}최대 부분 수열 합 문제를 해결하기 위해 동적 프로그래밍을 사용할 수도 있지만 문제를 해결하기 위해 분할 정복 알고리즘을 사용할 수도 있지만 최대 부분 수열 합은 다음과 같습니다. 단순 병합은 하위 시퀀스의 합에 길이 문제가 포함되므로 올바른 결과가 반드시 왼쪽이나 오른쪽에 있을 필요는 없지만 가능한 결과는 다음과 같습니다.
완전히 왼쪽에 있습니다. the middle
완전히 가운데의 오른쪽
가운데의 왼쪽과 오른쪽에 두 개의 노드를 포함하는 시퀀스
는 다음과 같이 그림으로 표현할 수 있습니다.
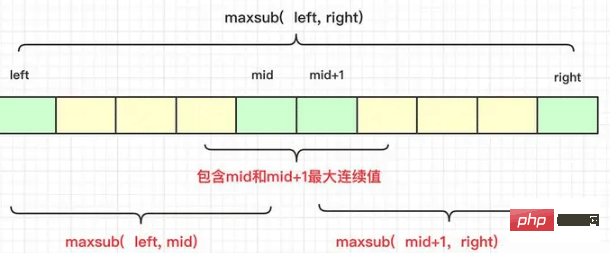
그래서 구체적으로 고려할 때 재귀 가능성을 배제할 필요가 있습니다. 구해진 결과 중간에 있는 최대값 문자열의 결과도 왼쪽과 오른쪽의 비교에 참여하도록 계산됩니다.
최대 하위 시퀀스 합을 위해 구현된 코드는 다음과 같습니다.
public int maxSubArray(int[] nums) {
int max=maxsub(nums,0,nums.length-1);
return max;
}
int maxsub(int nums[],int left,int right)
{
if(left==right)
return nums[left];
int mid=(left+right)/2;
int leftmax=maxsub(nums,left,mid);//左侧最大
int rightmax=maxsub(nums,mid+1,right);//右侧最大
int midleft=nums[mid];//中间往左
int midright=nums[mid+1];//中间往右
int team=0;
for(int i=mid;i>=left;i--)
{
team+=nums[i];
if(team>midleft)
midleft=team;
}
team=0;
for(int i=mid+1;i<=right;i++)
{
team+=nums[i];
if(team>midright)
midright=team;
}
int max=midleft+midright;//中间的最大值
if(max<leftmax)
max=leftmax;
if(max<rightmax)
max=rightmax;
return max;
}가장 가까운 점 쌍은 분할 및 정복의 매우 성공적인 응용 프로그램 중 하나입니다. 2차원 좌표축에는 여러 개의 점 좌표가 있어서 가장 가까운 두 점 사이의 거리를 구할 수 있습니다. 직접 찾아보라고 하면 열거 폭력은 아주 아주 많은 양의 계산을 사용합니다. 이런 종류의 문제를 최적화하기 위한 분할 정복 방법.
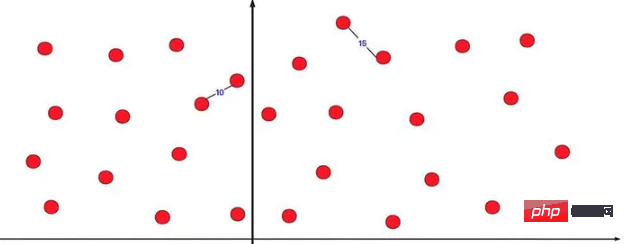
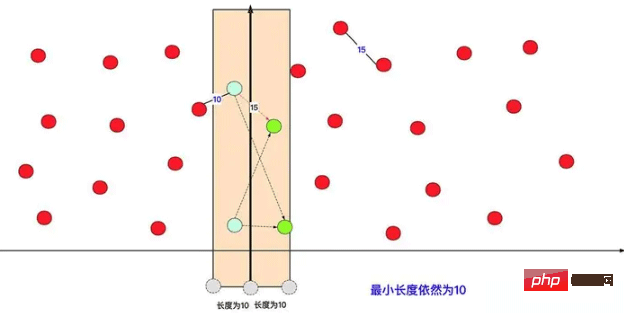
직접 두 부분으로 나누어서 분할 정복 계산을 해보면, 가장 짧은 것이 왼쪽에 하나, 오른쪽에 하나라면 문제가 있다는 걸 확실히 알 수 있을 것입니다. 우리는 그것을 최적화할 수 있습니다.
특정 최적화 계획에서는 x 또는 y 차원을 고려하여 데이터를 두 영역으로 나누고 먼저 (동일한 방법에 따라) 왼쪽 및 오른쪽 영역에서 각각 가장 짧은 점 쌍을 계산합니다. 그런 다음 둘 사이의 더 짧은 거리에 따라 왼쪽과 오른쪽으로 덮고 덮힌 왼쪽과 오른쪽 지점 사이의 거리를 계산하고 가장 작은 거리를 찾아 현재 최단 거리와 비교합니다.
이런 식으로 이 일회성 작업을 사용하면(하위 사례에 관계없이) 왼쪽의 빨간색 점은 오른쪽의 대부분의 빨간색 점과 함께 거리 계산을 피한다는 것을 알 수 있습니다(O의 시간 복잡도) (n2)). 실제로 왼쪽과 오른쪽 간격으로 내부 계산을 수행할 때 실제로는 많은 분할 정복 계산을 반복적으로 수행합니다. 그림에 표시된 대로:
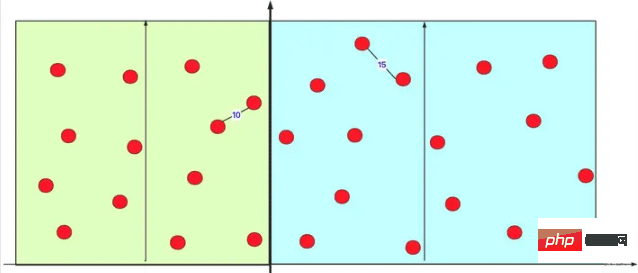
이렇게 하면 많은 계산을 절약할 수 있습니다.
그러나 이런 분할정복에는 문제가 있는데, 2차원 좌표점을 특정 방식, 특정 축으로 모두 모으면 효과가 뚜렷하지 않을 수 있다는 것입니다(점들이 모두 가깝습니다). x=2이고 x 나누기에 거의 영향을 미치지 않습니다. 주의가 필요합니다.
ac의 코드는
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.List;
public class Main {
static int n;
public static void main(String[] args) throws IOException {
StreamTokenizer in=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
//List<node>list=new ArrayList();
while(in.nextToken()!=StreamTokenizer.TT_EOF)
{
n=(int)in.nval;if(n==0) {break;}
node no[]=new node[n];
for(int i=0;i<n;i++)
{
in.nextToken();double x=in.nval;
in.nextToken();double y=in.nval;
// list.add(new node(x,y));
no[i]=new node(x,y);
}
Arrays.sort(no, com);
double min= search(no,0,n-1);
out.println(String.format("%.2f", Math.sqrt(min)/2));out.flush();
}
}
private static double search(node[] no, int left,int right) {
int mid=(right+left)/2;
double minleng=0;
if(left==right) {return Double.MAX_VALUE;}
else if(left+1==right) {minleng= (no[left].x-no[right].x)*(no[left].x-no[right].x)+(no[left].y-no[right].y)*(no[left].y-no[right].y);}
else minleng= min(search(no,left,mid),search(no,mid,right));
int ll=mid;int rr=mid+1;
while(no[mid].y-no[ll].y<=Math.sqrt(minleng)/2&&ll-1>=left) {ll--;}
while(no[rr].y-no[mid].y<=Math.sqrt(minleng)/2&&rr+1<=right) {rr++;}
for(int i=ll;i<rr;i++)
{
for(int j=i+1;j<rr+1;j++)
{
double team=0;
if(Math.abs((no[i].x-no[j].x)*(no[i].x-no[j].x))>minleng) {continue;}
else
{
team=(no[i].x-no[j].x)*(no[i].x-no[j].x)+(no[i].y-no[j].y)*(no[i].y-no[j].y);
if(team<minleng)minleng=team;
}
}
}
return minleng;
}
private static double min(double a, double b) {
// TODO 自动生成的方法存根
return a<b?a:b;
}
static Comparator<node>com=new Comparator<node>() {
@Override
public int compare(node a1, node a2) {
// TODO 自动生成的方法存根
return a1.y-a2.y>0?1:-1;
}};
static class node
{
double x;
double y;
public node(double x,double y)
{
this.x=x;
this.y=y;
}
}
}위 내용은 Java 알고리즘 설계 및 분석: 분할 정복 알고리즘 예제에 대한 자세한 설명의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!