덴드로그램은 개체, 그룹 또는 변수 간의 계층적 관계를 보여주는 다이어그램입니다. 덴드로그램은 유사한 특성을 가진 관측치 그룹을 나타내는 노드 또는 클러스터에 연결된 가지로 구성됩니다. 가지의 높이나 노드 사이의 거리는 그룹이 얼마나 다르거나 유사한지를 나타냅니다. 즉, 가지가 길수록 또는 노드 사이의 거리가 멀수록 그룹의 유사성은 줄어듭니다. 가지가 짧을수록 또는 노드 사이의 거리가 작을수록 그룹이 더 유사합니다.
Dendograms는 복잡한 데이터 구조를 시각화하고 유사한 특성을 가진 데이터의 하위 그룹 또는 클러스터를 식별하는 데 유용합니다. 이는 생물학, 유전학, 생태학, 사회 과학 및 유사성이나 상관 관계를 기반으로 데이터를 그룹화할 수 있는 기타 분야에서 일반적으로 사용됩니다.
배경 지식:
"dendrogram"이라는 단어는 그리스어 "dendron"(나무)와 "gramma"(그림)에서 유래되었습니다. 1901년 영국의 수학자이자 통계학자인 Karl Pearson은 다양한 식물 종 간의 관계를 보여주기 위해 수형도를 사용했습니다[1]. 그는 이 그래프를 "클러스터 그래프"라고 불렀습니다. 이는 덴드로그램의 첫 번째 사용으로 간주될 수 있습니다.
클러스터링을 위해 여러 회사의 실제 주가를 사용할 것입니다. 간편한 접근을 위해 Alpha Vantage에서 제공하는 무료 API를 사용하여 데이터를 수집합니다. Alpha Vantage는 무료 API와 프리미엄 API를 모두 제공합니다. API를 통해 액세스하려면 키가 필요합니다. 해당 웹사이트를 참조하세요.
import pandasaspd
import requests
companies={'Apple':'AAPL','Amazon':'AMZN','Facebook':'META','Tesla':'TSLA','Alphabet (Google)':'GOOGL','Shell':'SHEL','Suncor Energy':'SU',
'Exxon Mobil Corp':'XOM','Lululemon':'LULU','Walmart':'WMT','Carters':'CRI','Childrens Place':'PLCE','TJX Companies':'TJX',
'Victorias Secret':'VSCO','MACYs':'M','Wayfair':'W','Dollar Tree':'DLTR','CVS Caremark':'CVS','Walgreen':'WBA','Curaleaf':'CURLF'}기술, 소매, 석유 및 가스, 기타 산업 분야에서 선정된 20개 기업입니다.
import time
all_data={}
forkey,valueincompanies.items():
# Replace YOUR_API_KEY with your Alpha Vantage API key
url=f'https://www.alphavantage.co/query?function=TIME_SERIES_DAILY_ADJUSTED&symbol={value}&apikey=<YOUR_API_KEY>&outputsize=full'
response=requests.get(url)
data=response.json()
time.sleep(15)
if'Time Series (Daily)'indataanddata['Time Series (Daily)']:
df=pd.DataFrame.from_dict(data['Time Series (Daily)'], orient='index')
print(f'Received data for {key}')
else:
print("Time series data is empty or not available.")
df.rename(columns= {'1. open':key}, inplace=True)
all_data[key]=df[key]위 코드는 너무 자주 차단되지 않도록 API 호출 사이에 15초의 일시 중지를 설정합니다.
# find common dates among all data frames
common_dates=None
fordf_key, dfinall_data.items():
ifcommon_datesisNone:
common_dates=set(df.index)
else:
common_dates=common_dates.intersection(df.index)
common_dates=sorted(list(common_dates))
# create new data frame with common dates as index
df_combined=pd.DataFrame(index=common_dates)
# reindex each data frame with common dates and concatenate horizontally
fordf_key, dfinall_data.items():
df_combined=pd.concat([df_combined, df.reindex(common_dates)], axis=1)위의 데이터를 필요한 DF에 통합하면 바로 아래에서 사용할 수 있습니다.
계층적 클러스터링은 기계 학습 및 데이터 분석에 사용되는 클러스터링 알고리즘입니다. 중첩된 클러스터의 계층 구조를 사용하여 유사한 객체를 유사성을 기준으로 클러스터로 그룹화합니다. 알고리즘은 단일 개체로 시작하여 이를 클러스터로 병합하는 응집형이거나 큰 클러스터에서 시작하여 이를 더 작은 클러스터로 반복적으로 나누는 분할형일 수 있습니다.
모든 클러스터링 방법이 계층적 클러스터링 방법은 아니며 덴드로그램은 일부 클러스터링 알고리즘에서만 사용할 수 있다는 점에 유의해야 합니다.
클러스터링 알고리즘 scipy 모듈에서 제공하는 계층적 클러스터링을 사용하겠습니다.
1. 하향식 클러스터링
import numpyasnp import scipy.cluster.hierarchyassch import matplotlib.pyplotasplt # Convert correlation matrix to distance matrix dist_mat=1-df_combined.corr() # Perform top-down clustering clustering=sch.linkage(dist_mat, method='complete') cuts=sch.cut_tree(clustering, n_clusters=[3, 4]) # Plot dendrogram plt.figure(figsize=(10, 5)) sch.dendrogram(clustering, labels=list(df_combined.columns), leaf_rotation=90) plt.title('Dendrogram of Company Correlations (Top-Down Clustering)') plt.xlabel('Companies') plt.ylabel('Distance') plt.show()
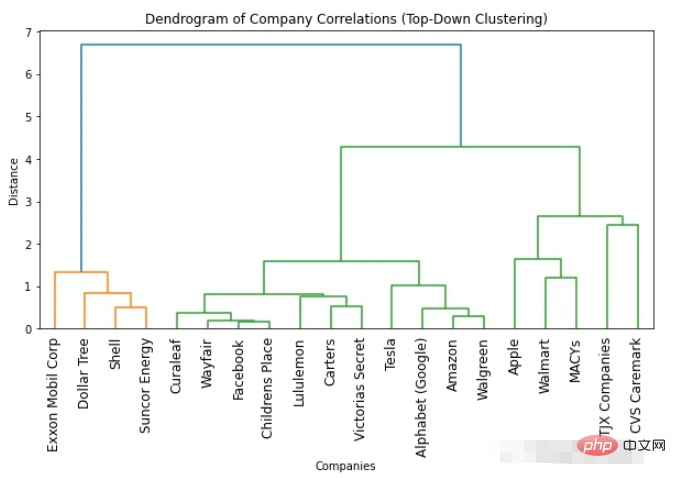
덴드로그램을 기반으로 최적의 클러스터 수를 결정하는 방법
최적의 클러스터 수를 찾는 가장 쉬운 방법은 생성된 덴드로그램을 살펴보는 것입니다. 색상의 수. 최적의 클러스터 수는 색상 수보다 하나 적습니다. 따라서 위의 덴드로그램에 따르면 최적의 클러스터 수는 2개입니다.
최적의 클러스터 수를 찾는 또 다른 방법은 클러스터 사이의 거리가 갑자기 변하는 지점을 식별하는 것입니다. 이를 "니 포인트" 또는 "엘보우 포인트"라고 하며 데이터의 변동을 가장 잘 포착하는 클러스터 수를 결정하는 데 사용할 수 있습니다. 위 그림에서 서로 다른 수의 클러스터 사이의 최대 거리 변화는 1개와 2개의 클러스터 사이에서 발생하는 것을 볼 수 있습니다. 따라서 최적의 클러스터 수는 2개입니다.
덴드로그램에서 원하는 개수의 클러스터 가져오기
덴드로그램 사용의 한 가지 장점은 덴드로그램을 보면 객체를 원하는 개수의 클러스터로 클러스터링할 수 있다는 것입니다. 예를 들어 두 개의 클러스터를 찾아야 하는 경우 덴드로그램의 위쪽 수직선을 보고 클러스터를 결정할 수 있습니다. 예를 들어, 이 예에서 두 개의 클러스터가 필요한 경우 첫 번째 클러스터에는 4개의 회사가 있고 두 번째 클러스터에는 16개의 회사가 있습니다. 3개의 클러스터가 필요한 경우 두 번째 클러스터를 11개 회사와 5개 회사로 추가로 분할할 수 있습니다. 더 필요한 경우 이 예를 따를 수 있습니다.
2. 상향식 클러스터링
import numpyasnp import scipy.cluster.hierarchyassch import matplotlib.pyplotasplt # Convert correlation matrix to distance matrix dist_mat=1-df_combined.corr() # Perform bottom-up clustering clustering=sch.linkage(dist_mat, method='ward') # Plot dendrogram plt.figure(figsize=(10, 5)) sch.dendrogram(clustering, labels=list(df_combined.columns), leaf_rotation=90) plt.title('Dendrogram of Company Correlations (Bottom-Up Clustering)') plt.xlabel('Companies') plt.ylabel('Distance') plt.show()
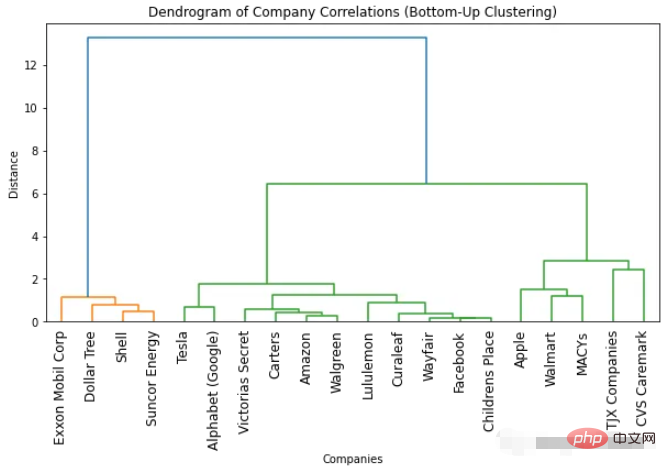
상향식 클러스터링으로 얻은 덴드로그램은 하향식 클러스터링과 유사합니다. 최적의 클러스터 수는 여전히 2개입니다(색상 수와 "변곡점" 방법을 기반으로 함). 그러나 더 많은 클러스터가 필요한 경우 약간의 미묘한 차이가 관찰됩니다. 이는 사용된 방법이 다르기 때문에 정상적인 현상이며 결과에 약간의 차이가 있을 수 있습니다.
위 내용은 Python에서 덴드로그램을 사용하여 시각적 클러스터링을 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!