Python에서 이진 트리를 구현하는 방법

Python은 이진 트리를 구현합니다

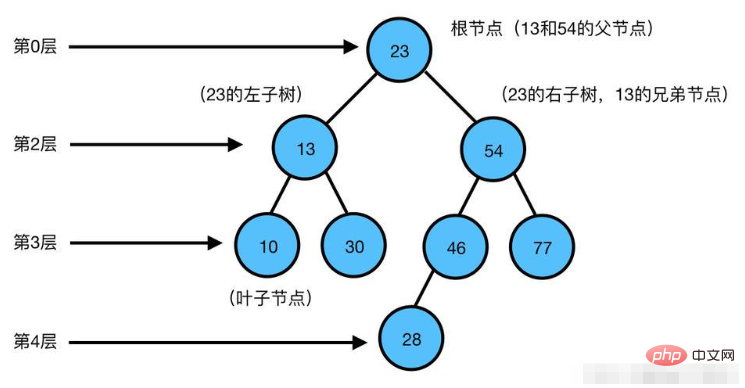
Python은 이진 트리 노드 클래스를 정의하여 객체 지향 프로그래밍을 사용하여 이진 트리를 구현할 수 있습니다. 각 노드에는 데이터 요소, 왼쪽 및 오른쪽 하위 노드 포인터 및 노드 삽입, 노드 찾기, 노드 삭제 등과 같은 일부 작업 방법이 포함되어 있습니다.

다음은 간단한 이진 트리 구현 예입니다.

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

    def insert(self, data):
        if self.data:
            if data < self.data:
                if self.left is None:
                    self.left = Node(data)
                else:
                    self.left.insert(data)
            elif data > self.data:
                if self.right is None:
                    self.right = Node(data)
                else:
                    self.right.insert(data)
        else:
            self.data = data

    def find(self, data):
        if data < self.data:
            if self.left is None:
                return str(data) + " Not Found"
            return self.left.find(data)
        elif data > self.data:
            if self.right is None:
                return str(data) + " Not Found"
            return self.right.find(data)
        else:
            return str(self.data) + " is found"

    def inorder_traversal(self, root):
        res = []
        if root:
            res = self.inorder_traversal(root.left)
            res.append(root.data)
            res = res + self.inorder_traversal(root.right)
        return res

위 코드에서 Node 클래스는 데이터 요소 데이터와 왼쪽 및 오른쪽 하위 노드 포인터를 포함하는 노드를 정의합니다. insert 메소드는 이진 트리에 노드를 삽입하는 데 사용되고, find 메소드는 이진 트리에 특정 노드가 존재하는지 찾는 데 사용되고, inorder_traversal 메소드는 이진 트리의 순차 순회를 수행하는 데 사용됩니다.

이 Node 클래스를 사용하여 이진 트리를 만드는 방법은 다음과 같습니다.

root = Node(50)
root.insert(30)
root.insert(20)
root.insert(40)
root.insert(70)
root.insert(60)
root.insert(80)

# 查找节点

print(root.find(70)) # Output: 70 is found
print(root.find(90)) # Output: 90 Not Found

# 中序遍历
print(root.inorder_traversal(root)) # Output: [20, 30, 40, 50, 60, 70, 80]

위 코드에서 루트 노드 루트가 먼저 생성된 다음 삽입 메서드를 사용하여 노드를 트리에 삽입하고 마지막으로 find 메서드를 사용합니다. 노드를 찾는 데 사용되고 inorder_traversal 메소드가 사용됩니다. 이진 트리의 중위 순회를 수행합니다.

삽입, 검색 및 순회 방법 외에도 이진 트리에는 노드 삭제, 이진 검색 트리인지 확인, 트리 깊이 계산 등과 같은 다른 작업 방법도 있습니다. 다음은 좀 더 완전한 이진 트리 샘플 코드입니다.

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

    def insert(self, data):
        if self.data:
            if data < self.data:
                if self.left is None:
                    self.left = Node(data)
                else:
                    self.left.insert(data)
            elif data > self.data:
                if self.right is None:
                    self.right = Node(data)
                else:
                    self.right.insert(data)
        else:
            self.data = data

    def find(self, data):
        if data < self.data:
            if self.left is None:
                return None
            return self.left.find(data)
        elif data > self.data:
            if self.right is None:
                return None
            return self.right.find(data)
        else:
            return self

    def delete(self, data):
        if self is None:
            return self

        if data < self.data:
            self.left = self.left.delete(data)
        elif data > self.data:
            self.right = self.right.delete(data)
        else:
            if self.left is None:
                temp = self.right
                self = None
                return temp
            elif self.right is None:
                temp = self.left
                self = None
                return temp
            temp = self.right.minimum()
            self.data = temp.data
            self.right = self.right.delete(temp.data)
        return self

    def minimum(self):
        if self.left is None:
            return self
        return self.left.minimum()

    def is_bst(self):
        if self.left:
            if self.left.data > self.data or not self.left.is_bst():
                return False

        if self.right:
            if self.right.data < self.data or not self.right.is_bst():
                return False

        return True

    def height(self, node):
        if node is None:
            return 0

        left_height = self.height(node.left)
        right_height = self.height(node.right)

        return max(left_height, right_height) + 1

    def inorder_traversal(self, root):
        res = []
        if root:
            res = self.inorder_traversal(root.left)
            res.append(root.data)
            res = res + self.inorder_traversal(root.right)
        return res

이 예에서는 지정된 노드를 삭제하는 삭제 메서드를 추가했습니다. 현재 트리는 트리의 깊이를 계산하는 이진 포크 검색 트리입니다.

다음 코드를 사용하여 새 방법을 테스트할 수 있습니다.

# 创建二叉树
root = Node(50)
root.insert(30)
root.insert(20)
root.insert(40)
root.insert(70)
root.insert(60)
root.insert(80)

# 删除节点
print("Deleting node 20:")
root.delete(20)
print(root.inorder_traversal(root))

# 判断是否为二叉搜索树
print("Is it a BST?:", root.is_bst())

# 计算树的深度
print("Tree height:", root.height(root))

이러한 방식으로 비교적 완전한 이진 트리 구현을 완료했으며 Python에서 객체 지향 프로그래밍 아이디어를 사용하여 데이터 구조를 구현하는 방법도 시연했습니다.

마지막으로 전체 이진 트리 클래스 구현 코드가 첨부됩니다.

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

    def insert(self, data):
        if self.data:
            if data < self.data:
                if self.left is None:
                    self.left = Node(data)
                else:
                    self.left.insert(data)
            elif data > self.data:
                if self.right is None:
                    self.right = Node(data)
                else:
                    self.right.insert(data)
        else:
            self.data = data

    def find(self, data):
        if data < self.data:
            if self.left is None:
                return None
            return self.left.find(data)
        elif data > self.data:
            if self.right is None:
                return None
            return self.right.find(data)
        else:
            return self

    def delete(self, data):
        if self is None:
            return self

        if data < self.data:
            self.left = self.left.delete(data)
        elif data > self.data:
            self.right = self.right.delete(data)
        else:
            if self.left is None:
                temp = self.right
                self = None
                return temp
            elif self.right is None:
                temp = self.left
                self = None
                return temp
            temp = self.right.minimum()
            self.data = temp.data
            self.right = self.right.delete(temp.data)
        return self

    def minimum(self):
        if self.left is None:
            return self
        return self.left.minimum()

    def is_bst(self):
        if self.left:
            if self.left.data > self.data or not self.left.is_bst():
                return False

        if self.right:
            if self.right.data < self.data or not self.right.is_bst():
                return False

        return True

    def height(self, node):
        if node is None:
            return 0

        left_height = self.height(node.left)
        right_height = self.height(node.right)

        return max(left_height, right_height) + 1

    def inorder_traversal(self, root):
        res = []
        if root:
            res = self.inorder_traversal(root.left)
            res.append(root.data)
            res = res + self.inorder_traversal(root.right)
        return res

if __name__ == '__main__':
    # 创建二叉树
    root = Node(50)
    root.insert(30)
    root.insert(20)
    root.insert(40)
    root.insert(70)
    root.insert(60)
    root.insert(80)

    # 删除节点
    print("Deleting node 20:")
    root.delete(20)
    print(root.inorder_traversal(root))

    # 判断是否为二叉搜索树
    print("Is it a BST?:", root.is_bst())

    # 计算树的深度
    print("Tree height:", root.height(root))

코드를 실행한 후 다음 출력을 얻을 수 있습니다.

노드 20 삭제:
[30, 40, 50, 60, 70, 80]
BST인가요?: True
트리 높이: 3

이 예제에는 삽입, 검색, 삭제, 순회, 이진 검색 트리인지 확인하고 트리 깊이 계산이 포함됩니다.

위 내용은 Python에서 이진 트리를 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!