지역 사회 배우다 도구 라이브러리 여가
찾다
한국어
집 > Java > java지도 시간 > Java 데이터 구조 및 알고리즘을 사용하여 재귀 및 역추적을 구현하는 방법

Java 데이터 구조 및 알고리즘을 사용하여 재귀 및 역추적을 구현하는 방법

WBOY
풀어 주다： 2023-05-06 08:28:06
앞으로
848명이 탐색했습니다.

1. 재귀란 무엇인가요?

간단히 말하면 재귀는 메소드가 호출될 때마다 다른 변수를 전달하는 것입니다. 재귀는 프로그래머가 복잡한 문제를 해결하고 코드를 간결하게 만드는 데 도움이 됩니다.

실제 응용 시나리오, 미로 문제(역추적), 재귀(재귀)를 살펴보세요

Java 데이터 구조 및 알고리즘을 사용하여 재귀 및 역추적을 구현하는 방법

재귀를 이해하는 데 도움이 되는 두 가지 작은 사례를 나열하겠습니다. 여기서는 재귀 호출 메커니즘을 검토하겠습니다.

  • 인쇄 문제

  • 팩토리얼 문제

public static void test(int n) {
    if (n > 2) {
	    test(n - 1);
    }
    System.out.println("n=" + n);
}
 
public static int factorial(int n) {
    if (n == 1) {
        return 1;
    } else {
        return factorial(n - 1) * n;
    }
}
로그인 후 복사

재귀를 사용하여 해결하는 문제는 무엇인가요?

  • 여러 여왕 문제, 하노이 탑, 계승 문제, 미로 문제, 공의 합 바구니 문제(구글 프로그래밍 대회).

  • 재귀는 퀵 정렬, 병합 정렬, 이진 검색, 분할 정복 알고리즘 등 다양한 알고리즘에도 사용됩니다.

  • 스택으로 해결될 문제-->코드가 비교적 간결합니다.

재귀를 위해 따라야 할 중요한 규칙

  • 메서드가 실행되면 보호되는 새로운 독립 공간(스택 공간)이 생성됩니다.

  • 메서드의 지역 변수는 독립적이며 n 변수와 같이 서로 영향을 주지 않습니다.

  • 메소드에 참조 유형 변수(예: 배열)가 사용되는 경우 참조 유형의 데이터가 공유됩니다.

  • 재귀는 재귀를 종료하기 위한 조건에 접근해야 합니다. 그렇지 않으면 무한 재귀가 되고 StackOverflowError가 나타나며 죽게 됩니다 :).

  • 메서드가 실행을 완료하거나 반환을 만나면 반환됩니다. 이를 호출하는 사람은 누구든지 호출하는 사람에게 결과를 반환합니다. 동시에 메서드가 실행을 완료하거나 반환하면 메서드도 실행을 완료합니다.

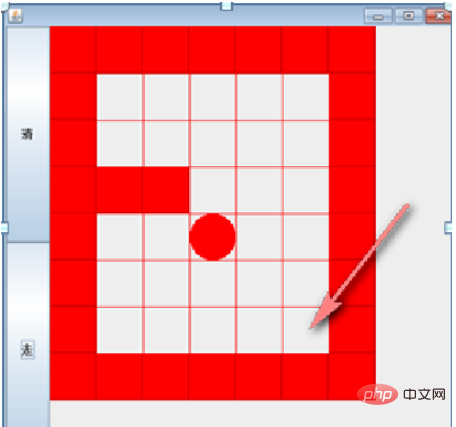
2. 코드 사례 1 - 미로 문제

설명: 공이 가는 경로는 프로그래머가 설정한 경로 찾기 전략, 즉 위쪽, 아래쪽, 왼쪽의 경로 찾기 순서와 관련됩니다. , 오른쪽은 공과 관련된 경로를 선택할 때 먼저 (오른쪽 아래, 왼쪽 위)를 사용한 다음 (오른쪽 위, 왼쪽 아래)로 변경하여 경로가 변경되는지 확인할 수 있습니다. 역추적 현상을 테스트합니다. 

package com.szh.recursion;
 
/**
 * 走迷宫问题
 */
public class MiGong {
 
    //使用递归回溯来给小球找路, 说明:
    //1. map 表示地图
    //2. i,j 表示从地图的哪个位置开始出发 (1,1)
    //3. 如果小球能到 map[6][5] 位置，则说明通路找到.
    //4. 约定：当 map[i][j] 为 0 表示该点没有走过; 当为 1 表示墙; 2 表示通路可以走;
    //5. 在走迷宫时，需要确定一个策略(方法) 下->右->上->左 , 如果该点走不通，再回溯
    public static boolean setWay(int[][] map, int i, int j) {
        //此时走到了迷宫终点
        if (map[6][5] == 2) {
            return true;
        } else {
            if (map[i][j] == 0) { //如果当前这个点还没有走过
                //按照策略 下->右->上->左  走
                map[i][j] = 2;
                if (setWay(map, i + 1, j)) { //下
                    return true;
                } else if (setWay(map, i, j + 1)) { //右
                    return true;
                } else if (setWay(map, i - 1, j)) { //上
                    return true;
                } else { //左
                    return true;
                }
            } else { //map[i][j] != 0, 即只能为1、2。 1表示墙（无法走），2表示已经走过了，所以此时直接返回false
                return false;
            }
        }
    }
 
    //修改找路的策略，改成 上->右->下->左
    public static boolean setWay2(int[][] map, int i, int j) {
        if(map[6][5] == 2) { // 通路已经找到ok
            return true;
        } else {
            if(map[i][j] == 0) { //如果当前这个点还没有走过
                //按照策略 上->右->下->左
                map[i][j] = 2;
                if(setWay2(map, i - 1, j)) { //上
                    return true;
                } else if (setWay2(map, i, j + 1)) { //右
                    return true;
                } else if (setWay2(map, i + 1, j)) { //下
                    return true;
                } else { //左
                    return true;
                }
            } else {
                return false;
            }
        }
    }
 
    public static void main(String[] args) {
        //先创建一个二维数组，模拟迷宫 (地图)
        int[][] map = new int[8][7];
        //使用迷宫中的部分格子表示墙体（置1）
        //第一行和最后一行置为1
        for (int i = 0; i < 7; i++) {
            map[0][i] = 1;
            map[7][i] = 1;
        }
        //第一列和最后一列置为1
        for (int i = 0; i < 8; i++) {
            map[i][0] = 1;
            map[i][6] = 1;
        }
        //多添加两块墙体
        map[3][1] = 1;
        map[3][2] = 1;
//      map[1][2] = 1;
//		map[2][2] = 1;
        //输出地图查看
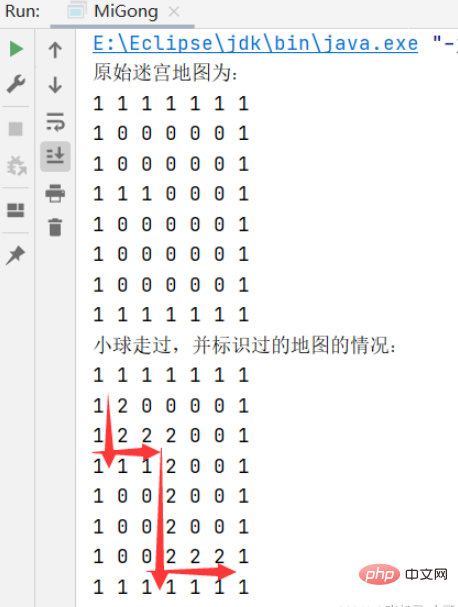
        System.out.println("原始迷宫地图为：");
        for (int i = 0; i < 8; i++) {
            for (int j = 0; j < 7; j++) {
                System.out.print(map[i][j] + " ");
            }
            System.out.println();
        }
 
        //使用递归回溯走迷宫
        setWay(map, 1, 1);
//        setWay2(map, 1, 1);
        System.out.println("小球走过，并标识过的地图的情况：");
        for (int i = 0; i < 8; i++) {
            for (int j = 0; j < 7; j++) {
                System.out.print(map[i][j] + " ");
            }
            System.out.println();
        }
    }
}
로그인 후 복사

Java 데이터 구조 및 알고리즘을 사용하여 재귀 및 역추적을 구현하는 방법

3. 코드 사례 2 - 여덟 여왕 문제

여덟 여왕 문제는 오래되고 유명한 문제이자 역추적 알고리즘의 전형적인 사례입니다. 이 문제는 1848년에 국제적인 체스 선수인 Max Bethel에 의해 제기되었습니다. 8×8 체스 격자에 8명의 여왕을 배치하여 서로 공격할 수 없도록 하십시오. 즉, 두 명의 여왕이 같은 위치에 있을 수 없습니다. 행, 열 또는 대각선으로?

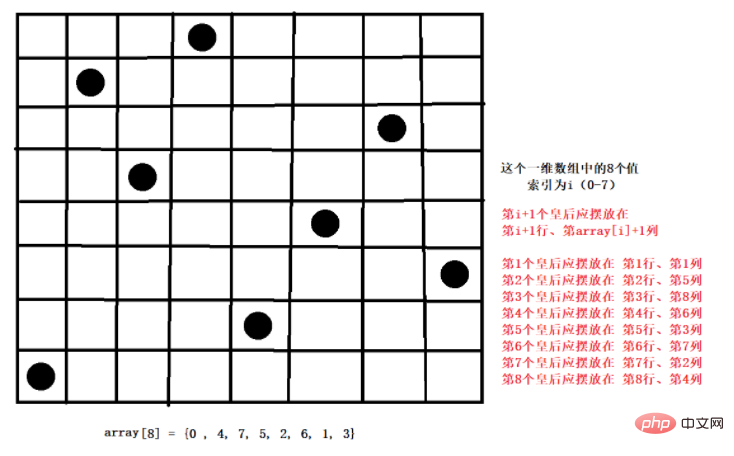
Java 데이터 구조 및 알고리즘을 사용하여 재귀 및 역추적을 구현하는 방법

첫 번째 퀸은 첫 번째 행과 첫 번째 열에 먼저 배치됩니다.

두 번째 퀸을 두 번째 행과 첫 번째 열에 배치한 다음 괜찮은지 확인하고 그렇지 않은 경우 계속해서 두 번째 열과 세 번째 열에 배치한 다음 모든 열을 배치하여 적합한 것을 찾습니다. .

계속해서 세 번째 퀸, 즉 첫 번째와 두 번째 열... 여덟 번째 퀸이 충돌하지 않는 위치에 배치될 수 있을 때까지는 올바른 해결책이라고 볼 수 있습니다.

올바른 솔루션을 얻었을 때 스택이 이전 스택으로 롤백되면 역추적을 시작합니다. 즉, 첫 번째 퀸을 첫 번째 열에 놓고 모든 올바른 솔루션을 얻습니다.

그런 다음 돌아가서 첫 번째 여왕을 두 번째 열에 계속 배치하고 1, 2, 3, 4단계를 반복해서 수행합니다. 

package com.szh.recursion;
 
/**
 * 八皇后问题
 */
public class Queue8 {
 
    //定义max表示共有多少个皇后
    private int max = 8;
    //定义数组，保存皇后放置的位置结果，比如 arr = {0, 4, 7, 5, 2, 6, 1, 3}
    int[] array = new int[max];
    //共有多少种解法
    private static int count = 0;
    //共有多少次冲突
    private static int judgeCount = 0;
 
    //编写一个方法，放置第n个皇后
    //特别注意： check 是 每一次递归时，进入到check中都有  for(int i = 0; i < max; i++)，因此会有回溯
    private void check(int n) {
        if (n == max) { //n = 8 , 表示这8个皇后已经全部放好了
            print();
            return;
        }
        //依次放入皇后，并判断是否冲突
        for (int i = 0; i < max; i++) {
            //先把当前这个皇后 n , 放到该行的第1列
            array[n] = i;
            //判断当放置第n个皇后到i列时，是否冲突
            if (judge(n)) { // 不冲突
                //接着放n+1个皇后,即开始递归
                check(n + 1);
            }
            //如果冲突，就继续执行 array[n] = i; 即将第n个皇后，放置在本行第i列向后的那一列
        }
    }
 
    //查看当我们放置第n个皇后, 就去检测该皇后是否和前面已经摆放的n-1个皇后冲突
    private boolean judge(int n) {
        //每摆放一个皇后，就循环去和之前摆好的皇后位置相比较，看是否冲突
        for (int i = 0; i < n; i++) {
            //1. array[i] == array[n]  表示判断 第n个皇后是否和前面的n-1个皇后在同一列
            //2. Math.abs(n-i) == Math.abs(array[n] - array[i]) 表示判断第n个皇后是否和第i皇后是否在同一斜线
            //3. 判断是否在同一行, 没有必要，n 表示第几个皇后，这个值每次都在递增，所以必然不在同一行
            if (array[i] == array[n] || Math.abs(n - i) == Math.abs(array[n] - array[i])) {
                judgeCount++;
                return false;
            }
        }
        return true;
    }
 
    //打印皇后摆放的具体位置
    private void print() {
        count++;
        for (int i = 0; i < array.length; i++) {
            System.out.print(array[i] + " ");
        }
        System.out.println();
    }
 
    public static void main(String[] args) {
        Queue8 queue8 = new Queue8();
        queue8.check(0);
        System.out.printf("一共有%d解法\n", count);
        System.out.printf("一共判断冲突的次数%d次", judgeCount);
    }
}
로그인 후 복사

Java 데이터 구조 및 알고리즘을 사용하여 재귀 및 역추적을 구현하는 방법

사실 코드를 디버깅하면 역추적 과정을 볼 수 있으니 더 말하지 않겠습니다.

위 내용은 Java 데이터 구조 및 알고리즘을 사용하여 재귀 및 역추적을 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

관련 라벨：
java
원천：yisu.com
이전 기사：Java 컬렉션의 구현 코드를 작성하는 방법 다음 기사：Java의 해시 테이블 분석 예
본 웹사이트의 성명
본 글의 내용은 네티즌들의 자발적인 기여로 작성되었으며, 저작권은 원저작자에게 있습니다. 본 사이트는 이에 상응하는 법적 책임을 지지 않습니다. 표절이나 침해가 의심되는 콘텐츠를 발견한 경우 admin@php.cn으로 문의하세요.
저자별 최신 기사
최신 이슈
자동 반올림 없이 JavaScript에서 문자열을 19자리 숫자로 변환하는 방법은 무엇입니까? 숫자로 변환하려는 경우 문자열 입력 숫자 input="6145390195186705543"(6145390195186705000)이 있습니다.
에서 2024-03-30 14:42:35
0
1
367
관련 주제
더>
인기 추천
인기 튜토리얼
더>
관련 튜토리얼
인기 추천
최신 강좌
최신 다운로드
더>
웹 효과
웹사이트 소스 코드
웹사이트 자료
프론트엔드 템플릿