Java의 해시 테이블 분석 예-java지도 시간-php.cn

1, 개념

순차 구조와 균형 트리에서는 요소의 키 코드와 저장 위치 사이에 대응 관계가 없으므로 요소 검색 시 키 코드의 다중 비교가 필요합니다. 만들어진. 순차탐색의 시간복잡도는 O(N)이다. 즉, 탐색과정에서 요소의 비교횟수에 따라 탐색의 효율성이 결정된다.

이상적인 검색 방법: 검색하려는 요소를 비교 없이 한 번에 테이블에서 직접 가져올 수 있습니다. 저장 구조를 구축하고 특정 함수(hashFunc)를 사용하여 요소의 저장 위치와 해당 키 코드 간의 일대일 매핑 관계를 설정하면 검색 시 이 함수를 통해 요소를 빠르게 찾을 수 있습니다.

이 구조에 요소를 삽입할 때:

요소 삽입

삽입할 요소의 키 코드에 따라 이 기능을 사용하여 요소의 저장 위치를 계산하고 이 위치에 따라 저장합니다

검색 for elements

요소의 키 코드 수행 동일한 계산에서 얻은 함수 값을 요소의 저장 위치로 간주하고 구조 내에서 이 위치에 따라 요소를 비교합니다. 검색이 성공했습니다

예: 데이터 세트 {1, 7, 6, 4, 5 , 9};

해시 함수는 다음과 같이 설정됩니다. hash(key) = key % 용량은 전체 크기입니다. 요소를 저장하기 위한 기본 공간입니다.

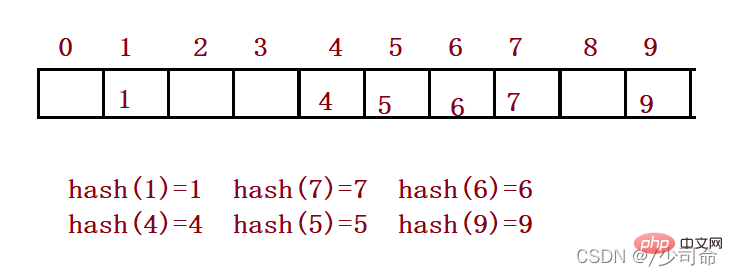
Java의 해시 테이블 분석 예

2. 충돌 방지

우선, 해시 테이블의 기본 배열 용량이 저장되는 실제 키워드 수보다 작은 경우가 많기 때문에 이는 다음과 같은 결과를 초래한다는 점을 분명히 해야 합니다. 갈등의 문제는 불가피하지만 우리가 할 수 있는 일은 갈등률을 최대한 줄이는 것이어야 한다.

3, 충돌-회피-해시 함수 설계

공용 해시 함수

직접 맞춤화 방법--(일반적으로 사용됨)

키워드의 선형 함수를 해시 주소로 사용: 해시(키) = A* 키 + B 장점: 단순하고 균일함 단점: 키워드의 분포를 미리 알아야 함 사용 시나리오: 상대적으로 작고 연속적인 상황을 찾는 데 적합

나머지를 나누어 남기는 방법 - (일반적으로 사용됨)

안에 허용되는 주소 수 설정 해시 테이블 m에 대해, m보다 크지 않지만 m과 가장 가깝거나 같은 소수 p를 해시 함수에 따라 취합니다: Hash(key) = key% p(p

중간 방법을 제곱--(이해)

키워드가 1234, 제곱이 1522756이라고 가정하고, 가운데 3자리 227을 해시 주소로 추출합니다. 또 다른 예는 키워드 4321, 제곱입니다. 18671041 입니다, 중간을 추출해 주세요 해시주소 제곱법보다 3자리 671(또는 710) 방식이 더 적합합니다. 키워드의 분포를 알 수 없고, 자릿수도 그리 크지 않습니다

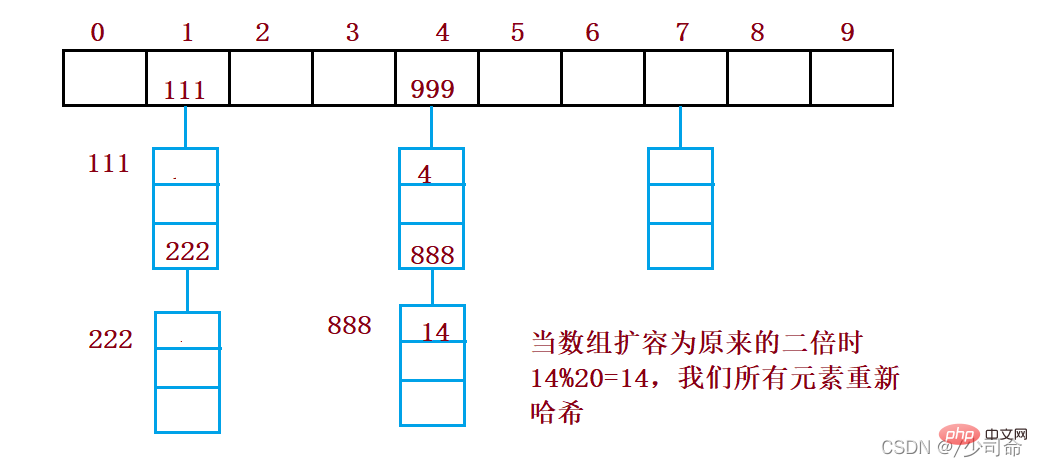
4, 갈등- 회피-부하율 조정

Java의 해시 테이블 분석 예

부하율과 충돌율의 관계에 대한 대략적인 시연

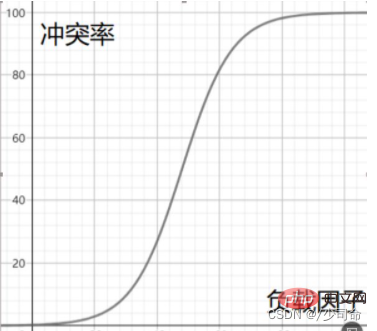
Java의 해시 테이블 분석 예

충돌율이 견딜 수 없는 수준에 도달하면 부하를 줄여 위장된 충돌율을 줄여야 합니다. 요인. , 해시 테이블의 키워드 수는 변경할 수 없는 것으로 알려져 있으므로 조정할 수 있는 것은 해시 테이블의 배열 크기뿐입니다.

5, 충돌 해결-폐쇄 해싱

폐쇄 해싱: 개방형 주소 지정 방법이라고도 합니다. 해시 충돌이 발생했을 때 해시 테이블이 가득 차지 않으면 해시 테이블에 빈 자리가 있어야 한다는 뜻입니다. 키는 충돌 위치의 "다음" 빈 위치에 저장될 수 있습니다.

①선형 감지

예를 들어 위 시나리오에서는 이제 요소 44를 삽입해야 합니다. 먼저 해시 함수를 통해 해시 주소를 계산합니다. 첨자는 4이므로 이론적으로는 이 위치에 44를 삽입해야 하지만 값이 이미 이 위치에 배치되어 있습니다. 요소가 4이면 해시 충돌이 발생합니다. 선형 감지: 충돌이 발생한 위치부터 시작하여 다음 빈 위치를 찾을 때까지 역방향으로 감지합니다.

Insert

해시 함수를 통해 해시 테이블에 삽입할 요소의 위치를 가져옵니다. 해당 위치에 요소가 없으면 새 요소를 직접 삽입합니다. 발생하면 선형 감지를 사용하여 다음 빈 요소를 찾습니다. 위치, 새 요소 삽입

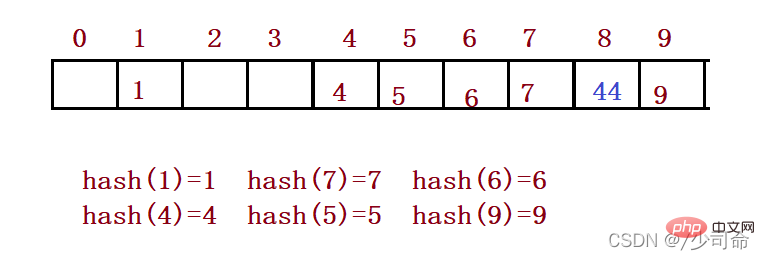
Java의 해시 테이블 분석 예

해시 충돌을 처리하기 위해 폐쇄형 해싱을 사용하는 경우 해시 테이블에서 기존 요소를 물리적으로 삭제할 수 없습니다. 요소를 직접 삭제하면 검색에 영향을 줍니다. 다른 요소의 경우. 예를 들어 요소 4를 직접 삭제하면 44에 대한 검색이 영향을 받을 수 있습니다. 따라서 선형 프로빙은 표시된 의사 삭제를 사용하여 요소를 삭제합니다.

②2차 검출

선형 검출의 결점은 충돌하는 데이터가 뭉쳐져 있다는 점인데, 이는 다음 빈 위치를 찾는 것과 관련이 있는데, 빈 위치를 찾는 방법은 하나씩 찾는 것이기 때문에 2차 검출은 피하는 것입니다. 이 문제에서 다음 빈 위치를 찾는 방법은 = ( + )% m 또는 = ( - )% m입니다. 그 중 i = 1,2,3...은 요소의 키 코드에서 해시 함수 Hash(x)에 의해 계산된 위치이고, m은 테이블의 크기입니다. 2.1의 경우 44를 삽입하려고 하면 충돌이 발생합니다. 솔루션 사용 후 상황은 다음과 같습니다.

Java의 해시 테이블 분석 예

연구에 따르면 테이블의 길이가 소수이고 테이블 로딩 계수 a가 0.5를 초과하지 않는 경우가 있습니다. , 새 테이블 항목은 확실히 삽입될 수 있으며 위치는 두 번 탐색되지 않습니다. 따라서 테이블에 빈 자리가 절반만 있는 한 테이블이 가득 차는 문제는 발생하지 않습니다. 검색 시에는 테이블이 꽉 찼다고 생각할 필요는 없으나, 삽입 시에는 테이블의 부하율 a가 0.5를 넘지 않는지 확인해야 하며, 초과할 경우 용량을 늘리는 것을 고려해야 합니다.

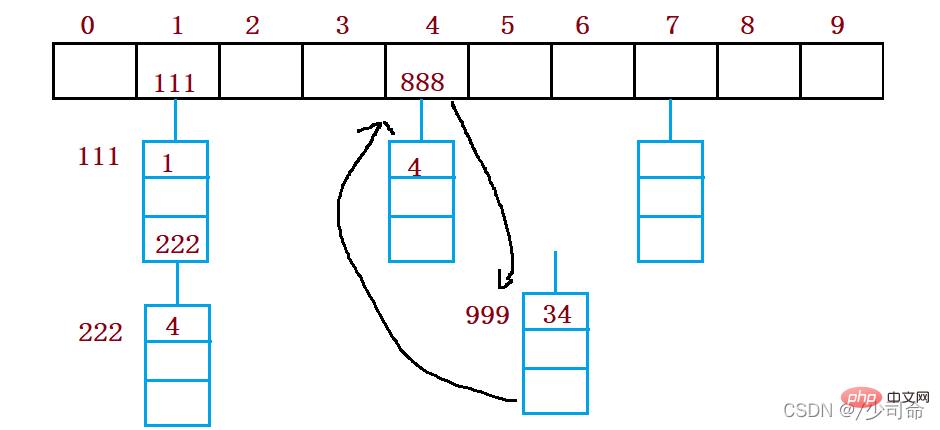
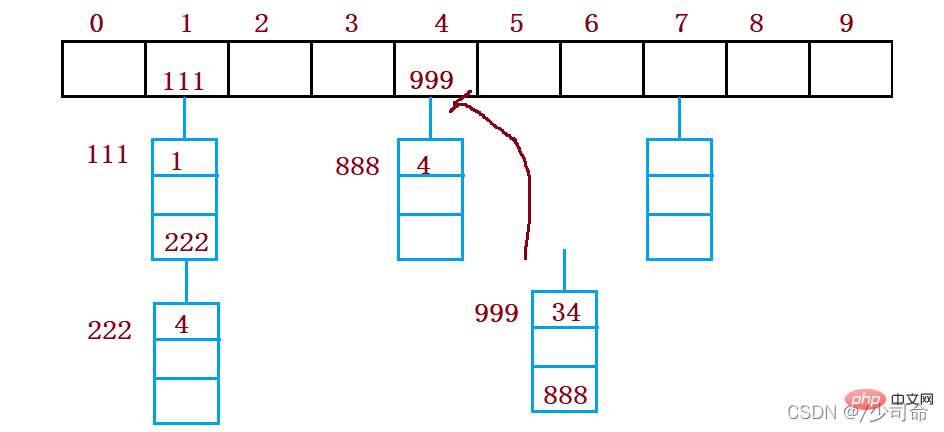
6, 충돌 해결-오픈 해시/해시 버킷

오픈 해시 방식은 체인 주소 방식(오픈 체인 방식)이라고도 합니다. 먼저 해시 함수를 사용하여 키 코드 세트의 해시 주소를 계산합니다. 동일한 주소 Key code를 가진 것들은 동일한 하위 집합에 속하며, 각 하위 집합을 버킷이라고 합니다. 각 버킷의 요소는 단일 연결 목록을 통해 연결되며, 각 연결 목록의 헤드 노드는 버킷에 저장됩니다. 해시 테이블.

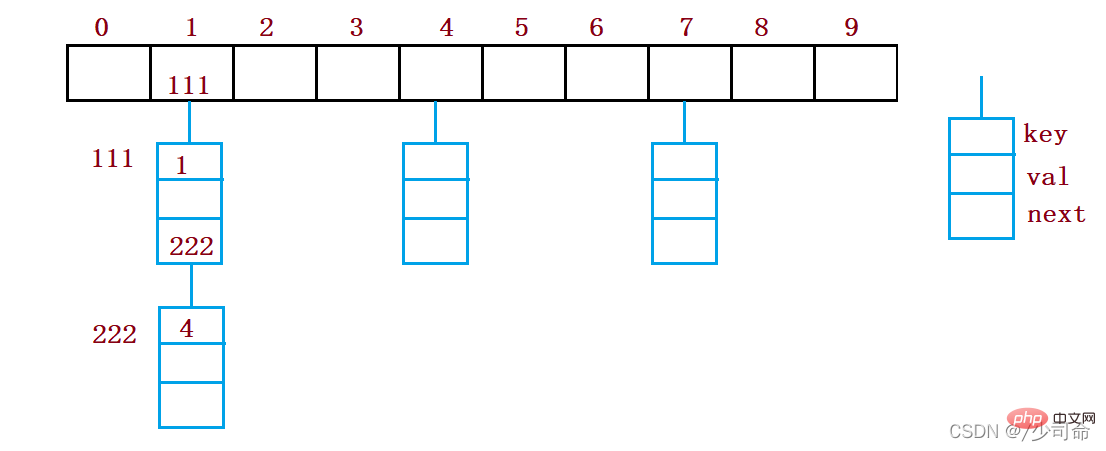
Java의 해시 테이블 분석 예

 
     static class Node {
         public int key;
         public int val;
         public Node next;
 
         public Node(int key, int val) {
             this.key = key;
             this.val = val;
         }
     }
 
     private Node[] array;
     public int usedSize;
 
     public HashBucket() {
         this.array = new Node[10];
         this.usedSize = 0;
     }

로그인 후 복사

Java의 해시 테이블 분석 예

 public void put(int key,int val){
        int index = key % this.array.length;
        Node cur = array[index];
        while (cur != null){
            if(cur.val == key){
                cur.val = val;
                return;
            }
            cur = cur.next;
        }
        //头插法
         Node node = new Node(key,val);
        node.next = array[index];
        array[index] = node;
        this.usedSize++;
        if(loadFactor() >= 0.75){
            resize();
        }
    }

로그인 후 복사

public int get(int key) {
         //以什么方式存储的  那就以什么方式取
         int index = key % this.array.length;
         Node cur = array[index];
         while (cur != null) {
             if(cur.key == key) {
                 return cur.val;
             }
             cur = cur.next;
         }
         return -1;//
     }

로그인 후 복사

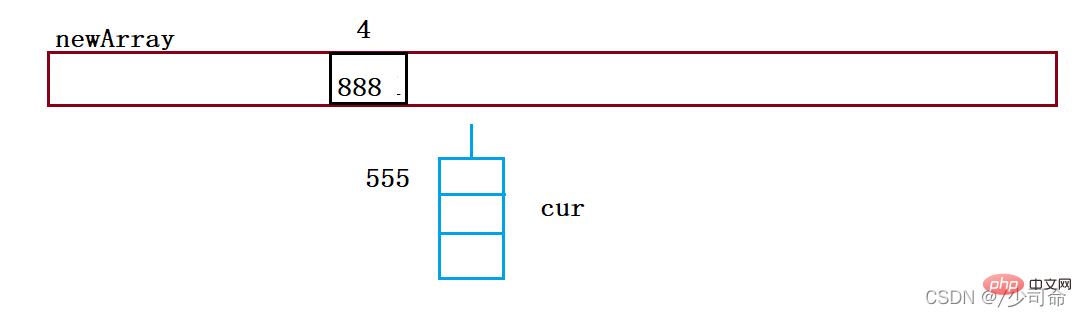
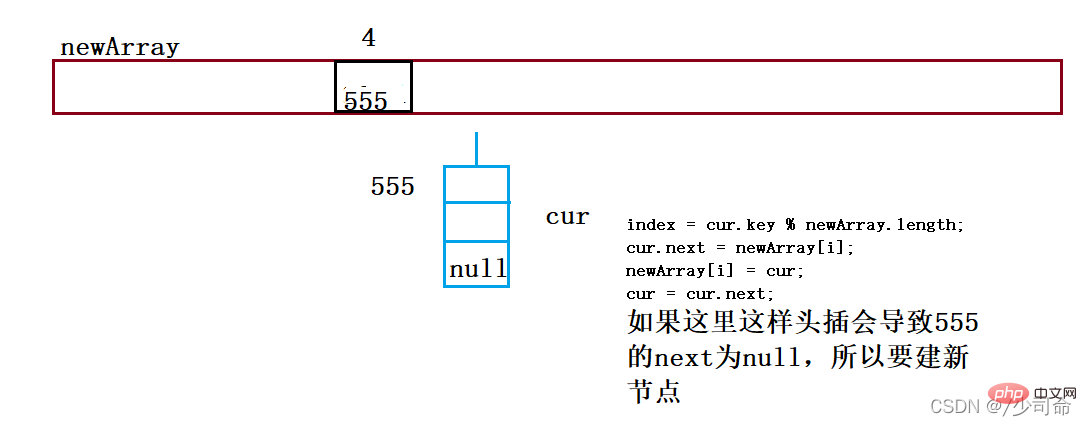
Java의 해시 테이블 분석 예

public void resize(){
 
        Node[] newArray = new Node[2*this.array.length];
        for (int i = 0; i < this.array.length; i++){
            Node cur = array[i];
            Node curNext = null;
            while (cur != null){
 
                curNext = cur.next;
                int index = cur.key % newArray.length;
                cur.next = newArray[i];
                newArray[i] = cur;
                cur = curNext.next;
                cur = curNext;
 
            }
        }
        this.array = newArray;
    }

로그인 후 복사

7, 전체 코드

 class HashBucket {
 
     static class Node {
         public int key;
         public int val;
         public Node next;
 
         public Node(int key, int val) {
             this.key = key;
             this.val = val;
         }
     }
 
     private Node[] array;
     public int usedSize;
 
     public HashBucket() {
         this.array = new Node[10];
         this.usedSize = 0;
     }
 
     public void put(int key,int val) {
         //1、确定下标
         int index = key % this.array.length;
         //2、遍历这个下标的链表
         Node cur = array[index];
         while (cur != null) {
             //更新val
             if(cur.key == key) {
                 cur.val = val;
                 return;
             }
             cur = cur.next;
         }
         //3、cur == null   当前数组下标的 链表  没要key
         Node node = new Node(key,val);
         node.next = array[index];
         array[index] = node;
         this.usedSize++;
         //4、判断  当前 有没有超过负载因子
         if(loadFactor() >= 0.75) {
             //扩容
             resize();
         }
     }
 
     public int get(int key) {
         //以什么方式存储的  那就以什么方式取
         int index = key % this.array.length;
         Node cur = array[index];
         while (cur != null) {
             if(cur.key == key) {
                 return cur.val;
             }
             cur = cur.next;
         }
         return -1;//
     }
 
 
     public double loadFactor() {
         return this.usedSize*1.0 / this.array.length;
     }
 
 
 
    public void resize(){
 
        Node[] newArray = new Node[2*this.array.length];
        for (int i = 0; i < this.array.length; i++){
            Node cur = array[i];
            Node curNext = null;
            while (cur != null){
 
                curNext = cur.next;
                int index = cur.key % newArray.length;
                cur.next = newArray[i];
                newArray[i] = cur;
                cur = curNext.next;
                cur = curNext;
 
            }
        }
        this.array = newArray;
    }
 
 
}

로그인 후 복사

위 내용은 Java의 해시 테이블 분석 예의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!