그럼 시작하기 전에 기본적인 PSO 알고리즘에 대해 이야기해보겠습니다. 핵심은 단 하나입니다.
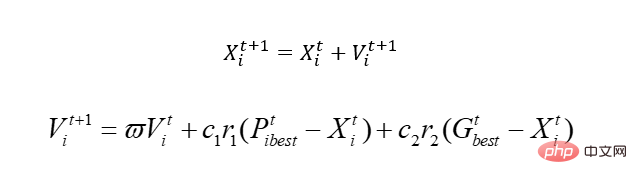
이 공식을 설명하면 이해하게 될 것입니다.
기존 규칙: 우리는 방정식 y=sin(x1)+cos(x2)
PSO 알고리즘이 새 이동을 시뮬레이션하여 최적화를 달성한다고 가정합니다. 이것이 어떻게 발생했는지는 다루지 않겠습니다. 핵심 .
방금 우리가 준 방정식에는 x1과 x2라는 두 개의 변수가 있습니다. 모의 새이기 때문에 블라인드 방식을 구현하기 위해 여기서는 속도 개념을 도입하고, x는 당연히 우리의 실현 가능 영역인 해 공간이다. 속도를 변경하면 x가 이동합니다. 즉, x의 값이 변경됩니다. 그 중 Pbest는 새가 걸어온 위치에서의 최적 솔루션을 나타내고, Gbest는 전체 개체군에 대한 최적 솔루션을 나타냅니다. 무슨 뜻입니까? 즉, 이 새가 움직일 때 더 나쁜 위치로 이동할 수 있다는 것입니다. 왜냐하면 유전학과는 달리 이 새는 나쁘면 죽겠지만 이 새는 그렇지 않기 때문입니다. 물론, 관련된 많은 지역적 문제가 있으므로 여기서는 논의하지 않겠습니다. 어떤 알고리즘도 완벽하지 않으며 이것이 옳습니다.
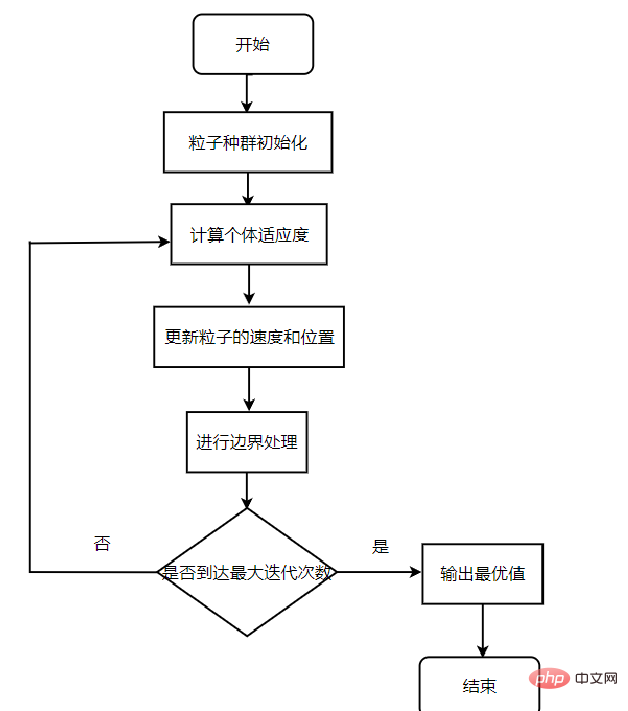
알고리즘의 주요 프로세스:
1단계: 입자 떼의 무작위 위치와 속도를 초기화하고 반복 횟수를 설정합니다.
2단계: 각 입자의 적합도 값을 계산합니다.
3단계: 각 입자에 대해 자신의 체력 값을 내가 경험한 최고의 위치의 체력 값과 비교합니다. 더 좋으면 현재 개인의 최적 위치로 사용합니다.
4단계: 각 입자에 대해 해당 적합도 값을 gbestg가 경험한 전 세계 최고 위치의 적합도 값과 비교합니다. 더 나은 경우 현재 전역 최적 위치로 사용합니다.
5단계: 속도 및 위치 공식에 따라 입자의 속도와 위치를 최적화하여 입자 위치를 업데이트합니다.
6단계: 종료 조건(일반적으로 최대 사이클 수 또는 최소 오류 요구 사항)에 도달하지 않으면 두 번째 단계로 돌아갑니다.
장점:
PSO 알고리즘에는 교차 및 돌연변이 연산이 없습니다. 검색을 완료하기 위해 입자 속도에 의존하며, 반복적인 진화에서는 최적의 입자만이 다른 입자에 정보를 전달하며 검색 속도가 빠릅니다.
PSO 알고리즘에는 메모리가 있으며, 입자 그룹의 역사적 최고 위치를 기억하여 다른 입자에 전달할 수 있습니다.
조정해야 할 매개변수가 적고 구조가 간단하며 엔지니어링에서 구현하기 쉽습니다.
실수 인코딩을 사용하여 문제 풀이의 변수 수를 입자의 차원으로 직접 사용합니다.
단점:
속도의 동적 조정이 부족하고 쉽게 지역적 최적성에 빠지기 때문에 수렴 정확도가 낮고 수렴이 어렵습니다.
이산 및 조합 최적화 문제를 효과적으로 해결할 수 없습니다.
매개변수 제어, 다양한 문제에 대해 최적의 결과를 얻기 위해 적절한 매개변수를 선택하는 방법.
일부 비데카르트 좌표계 설명 문제를 효과적으로 해결할 수 없습니다.
좋습니다. 가장 간단한 구현을 살펴보겠습니다.
import numpy as np
import random
class PSO_model:
def __init__(self,w,c1,c2,r1,r2,N,D,M):
self.w = w # 惯性权值
self.c1=c1
self.c2=c2
self.r1=r1
self.r2=r2
self.N=N # 初始化种群数量个数
self.D=D # 搜索空间维度
self.M=M # 迭代的最大次数
self.x=np.zeros((self.N,self.D)) #粒子的初始位置
self.v=np.zeros((self.N,self.D)) #粒子的初始速度
self.pbest=np.zeros((self.N,self.D)) #个体最优值初始化
self.gbest=np.zeros((1,self.D)) #种群最优值
self.p_fit=np.zeros(self.N)
self.fit=1e8 #初始化全局最优适应度
# 目标函数，也是适应度函数（求最小化问题）
def function(self,x):
A = 10
x1=x[0]
x2=x[1]
Z = 2 * A + x1 ** 2 - A * np.cos(2 * np.pi * x1) + x2 ** 2 - A * np.cos(2 * np.pi * x2)
return Z
# 初始化种群
def init_pop(self):
for i in range(self.N):
for j in range(self.D):
self.x[i][j] = random.random()
self.v[i][j] = random.random()
self.pbest[i] = self.x[i] # 初始化个体的最优值
aim=self.function(self.x[i]) # 计算个体的适应度值
self.p_fit[i]=aim # 初始化个体的最优位置
if aim < self.fit: # 对个体适应度进行比较，计算出最优的种群适应度
self.fit = aim
self.gbest = self.x[i]
# 更新粒子的位置与速度
def update(self):
for t in range(self.M): # 在迭代次数M内进行循环
for i in range(self.N): # 对所有种群进行一次循环
aim=self.function(self.x[i]) # 计算一次目标函数的适应度
if aim<self.p_fit[i]: # 比较适应度大小，将小的负值给个体最优
self.p_fit[i]=aim
self.pbest[i]=self.x[i]
if self.p_fit[i]<self.fit: # 如果是个体最优再将和全体最优进行对比
self.gbest=self.x[i]
self.fit = self.p_fit[i]
for i in range(self.N): # 更新粒子的速度和位置
self.v[i]=self.w*self.v[i]+self.c1*self.r1*(self.pbest[i]-self.x[i])+ self.c2*self.r2*(self.gbest-self.x[i])
self.x[i]=self.x[i]+self.v[i]
print("最优值：",self.fit,"位置为：",self.gbest)
if __name__ == '__main__':
# w,c1,c2,r1,r2,N,D,M参数初始化
w=random.random()
c1=c2=2#一般设置为2
r1=0.7
r2=0.5
N=30
D=2
M=200
pso_object=PSO_model(w,c1,c2,r1,r2,N,D,M)#设置初始权值
pso_object.init_pop()
pso_object.update()해결
# 群体的初始化和路径的初始化
self.population = np.array([0] * self.num_pop * self.num).reshape(
self.num_pop, self.num)
self.fitness = [0] * self.num_pop
"""
计算城市的距离，我们用矩阵表示城市间的距离
"""
self.__matrix_distance = self.__matrix_dis()와 원래 PSO의 가장 큰 차이점은 무엇인가요? 이는 실제로 간단하며 업데이트 속도와 관련이 있습니다. 지속적인 문제를 다룰 때 실제로는 다음과 같습니다.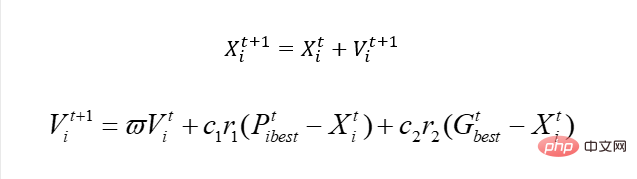 
마찬가지로 X를 사용하여 도시의 수를 나타낼 수 있지만 분명히 이 솔루션을 사용하여 속도를 업데이트할 수는 없습니다.
이때 속도를 업데이트하려면 새로운 솔루션을 사용해야 합니다. 따라서 이 솔루션은 실제로 유전자 알고리즘을 사용한 X 업데이트입니다. 직설적으로 말하면, 속도가 필요한 이유는 X를 업데이트하여 X를 좋은 방향으로 움직이게 하기 위해서입니다. 이제는 더 이상 단순히 속도 업데이트를 사용하는 것이 불가능하므로 어차피 X를 업데이트하고 있으니 그냥 이 X를 잘 업데이트할 수 있는 솔루션을 선택하면 되지 않을까요? 따라서 여기서 유전학을 직접 사용할 수 있습니다. 우리의 속도 업데이트는 Pbest와 Gbest를 기반으로 한 다음 특정 가중치에 따라 "학습"됩니다. 이러한 방식으로 이 V는 Pbest와 Gbest의 "특성"을 갖습니다. 그렇다면, 유전자 교배를 직접 모방해서 베스트와 교배시키면 그에 상응하는 "특징"을 배울 수는 없는 걸까요?
def cross_1(self, path, best_path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
left, right = min(r1, r2), max(r1, r2)
cross = best_path[left:right + 1]
for i in range(right - left + 1):
for k in range(self.num):
if path[k] == cross[i]:
path[k:self.num - 1] = path[k + 1:self.num]
path[-1] = 0
path[self.num - right + left - 1:self.num] = cross
return path def mutation(self,path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
path[r1],path[r2] = path[r2],path[r1]
return path전체 코드
🎜좋아, 이제 전체 코드를 살펴보자:🎜import numpy as np
import matplotlib.pyplot as plt
class HybridPsoTSP(object):
def __init__(self ,data ,num_pop=200):
self.num_pop = num_pop # 群体个数
self.data = data # 城市坐标
self.num =len(data) # 城市个数
# 群体的初始化和路径的初始化
self.population = np.array([0] * self.num_pop * self.num).reshape(
self.num_pop, self.num)
self.fitness = [0] * self.num_pop
"""
计算城市的距离，我们用矩阵表示城市间的距离
"""
self.__matrix_distance = self.__matrix_dis()
def __matrix_dis(self):
"""
计算14个城市的距离，将这些距离用矩阵存起来
:return:
"""
res = np.zeros((self.num, self.num))
for i in range(self.num):
for j in range(i + 1, self.num):
res[i, j] = np.linalg.norm(self.data[i, :] - self.data[j, :])
res[j, i] = res[i, j]
return res
def cross_1(self, path, best_path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
left, right = min(r1, r2), max(r1, r2)
cross = best_path[left:right + 1]
for i in range(right - left + 1):
for k in range(self.num):
if path[k] == cross[i]:
path[k:self.num - 1] = path[k + 1:self.num]
path[-1] = 0
path[self.num - right + left - 1:self.num] = cross
return path
def mutation(self,path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
path[r1],path[r2] = path[r2],path[r1]
return path
def comp_fit(self, one_path):
"""
计算，咱们这个路径的长度，例如A-B-C-D
:param one_path:
:return:
"""
res = 0
for i in range(self.num - 1):
res += self.__matrix_distance[one_path[i], one_path[i + 1]]
res += self.__matrix_distance[one_path[-1], one_path[0]]
return res
def out_path(self, one_path):
"""
输出我们的路径顺序
:param one_path:
:return:
"""
res = str(one_path[0] + 1) + '-->'
for i in range(1, self.num):
res += str(one_path[i] + 1) + '-->'
res += str(one_path[0] + 1) + '\n'
print(res)
def init_population(self):
"""
初始化种群
:return:
"""
rand_ch = np.array(range(self.num))
for i in range(self.num_pop):
np.random.shuffle(rand_ch)
self.population[i, :] = rand_ch
self.fitness[i] = self.comp_fit(rand_ch)
def main(data, max_n=200, num_pop=200):
Path_short = HybridPsoTSP(data, num_pop=num_pop) # 混合粒子群算法类
Path_short.init_population() # 初始化种群
# 初始化路径绘图
fig, ax = plt.subplots()
x = data[:, 0]
y = data[:, 1]
ax.scatter(x, y, linewidths=0.1)
for i, txt in enumerate(range(1, len(data) + 1)):
ax.annotate(txt, (x[i], y[i]))
res0 = Path_short.population[0]
x0 = x[res0]
y0 = y[res0]
for i in range(len(data) - 1):
plt.quiver(x0[i], y0[i], x0[i + 1] - x0[i], y0[i + 1] - y0[i], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.quiver(x0[-1], y0[-1], x0[0] - x0[-1], y0[0] - y0[-1], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.show()
print('初始染色体的路程: ' + str(Path_short.fitness[0]))
# 存储个体极值的路径和距离
best_P_population = Path_short.population.copy()
best_P_fit = Path_short.fitness.copy()
min_index = np.argmin(Path_short.fitness)
# 存储当前种群极值的路径和距离
best_G_population = Path_short.population[min_index, :]
best_G_fit = Path_short.fitness[min_index]
# 存储每一步迭代后的最优路径和距离
best_population = [best_G_population]
best_fit = [best_G_fit]
# 复制当前群体进行交叉变异
x_new = Path_short.population.copy()
for i in range(max_n):
# 更新当前的个体极值
for j in range(num_pop):
if Path_short.fitness[j] < best_P_fit[j]:
best_P_fit[j] = Path_short.fitness[j]
best_P_population[j, :] = Path_short.population[j, :]
# 更新当前种群的群体极值
min_index = np.argmin(Path_short.fitness)
best_G_population = Path_short.population[min_index, :]
best_G_fit = Path_short.fitness[min_index]
# 更新每一步迭代后的全局最优路径和解
if best_G_fit < best_fit[-1]:
best_fit.append(best_G_fit)
best_population.append(best_G_population)
else:
best_fit.append(best_fit[-1])
best_population.append(best_population[-1])
# 将每个个体与个体极值和当前的群体极值进行交叉
for j in range(num_pop):
# 与个体极值交叉
x_new[j, :] = Path_short.cross_1(x_new[j, :], best_P_population[j, :])
fit = Path_short.comp_fit(x_new[j, :])
# 判断是否保留
if fit < Path_short.fitness[j]:
Path_short.population[j, :] = x_new[j, :]
Path_short.fitness[j] = fit
# 与当前极值交叉
x_new[j, :] = Path_short.cross_1(x_new[j, :], best_G_population)
fit = Path_short.comp_fit(x_new[j, :])
if fit < Path_short.fitness[j]:
Path_short.population[j, :] = x_new[j, :]
Path_short.fitness[j] = fit
# 变异
x_new[j, :] = Path_short.mutation(x_new[j, :])
fit = Path_short.comp_fit(x_new[j, :])
if fit <= Path_short.fitness[j]:
Path_short.population[j] = x_new[j, :]
Path_short.fitness[j] = fit
if (i + 1) % 20 == 0:
print('第' + str(i + 1) + '步后的最短的路程: ' + str(Path_short.fitness[min_index]))
print('第' + str(i + 1) + '步后的最优路径:')
Path_short.out_path(Path_short.population[min_index, :]) # 显示每一步的最优路径
Path_short.best_population = best_population
Path_short.best_fit = best_fit
return Path_short # 返回结果类
if __name__ == '__main__':
data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))
main(data)初始染色体的路程: 71.30211569672313
第20步后的最短的路程: 29.340520066994223
第20步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第40步后的最短的路程: 29.340520066994223
第40步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第60步后的最短的路程: 29.340520066994223
第60步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第80步后的最短的路程: 29.340520066994223
第80步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第100步后的最短的路程: 29.340520066994223
第100步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第120步后的最短的路程: 29.340520066994223
第120步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第140步后的最短的路程: 29.340520066994223
第140步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第160步后的最短的路程: 29.340520066994223
第160步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第180步后的最短的路程: 29.340520066994223
第180步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第200步后的最短的路程: 29.340520066994223
第200步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
可以看到收敛速度还是很快的。
ok,到目前为止的话，我们介绍了两个算法去解决TSP或者是优化问题。我们来分析一下，这些算法有什么特点，为啥可以达到我们需要的优化效果。其实不管是遗传还是PSO，你其实都可以发现，有一个东西，我们可以暂且叫它环境压力。我们通过物竞天择，或者鸟类迁移，进行模拟寻优。而之所以需要这样做，是因为我们指定了一个规则，在我们的规则之下。我们让模拟的种群有一种压力去靠拢，其中物竞天择和鸟类迁移只是我们的一种手段，去应对这样的“压力”。所以的对于这种算法而言，最核心的点就两个：
我们需要做优化问题，所以我们必须要能够让我们的解往那个方向走，需要一个驱动，需要一个压力。因此我们需要设计这样的一个环境，在遗传算法，粒子群算法是通过种群当中的生存，来进行设计的它的压力是我们的目标函数。由种群和目标函数（目标指标）构成了一个环境和压力。
之后的话，我们设计好了一个环境和压力，那么未来应对这种压力，我们需要去设计一种策略，来应付这种压力。遗传算法是通过PUA自己，也就是种群的优胜略汰。PSO是通过学习，学习种群的优秀粒子和过去自己家的优秀“祖先”来应对这种压力的。
所以的话，我们是否可以使用别的方案来实现这种优化效果。，在强化学习的算法框架里面的话，我们明确的知道了为什么他们可以实现优化，是环境压力+压力策略。恰好咱们强化学习是有环境的，适应函数和环境恰好可以组成环境+压力。本身的算法收敛过程就是我们的压力策略。所以我们完全是可以直接使用强化学习进行这个处理的。那么在这里咱们就来使用强化学习在下一篇文章当中。
위 내용은 TSP 문제를 해결하기 위해 Python을 사용하여 PSO 알고리즘을 구현하는 방법은 무엇입니까?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
![[웹 프런트엔드] Node.js 빠른 시작](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
