몬테카를로 시뮬레이션은 확률 통계에 기반한 방법으로, 무작위 시뮬레이션을 사용하여 사건이 발생할 확률을 계산합니다. 프로젝트 관리에서 몬테카를로 시뮬레이션은 프로젝트 기간, 비용 등 주요 지표의 확률 분포를 계산하는 데 주로 사용되어 프로젝트 관리자가 위험을 더 잘 관리하고 의사 결정을 내릴 수 있도록 돕습니다.
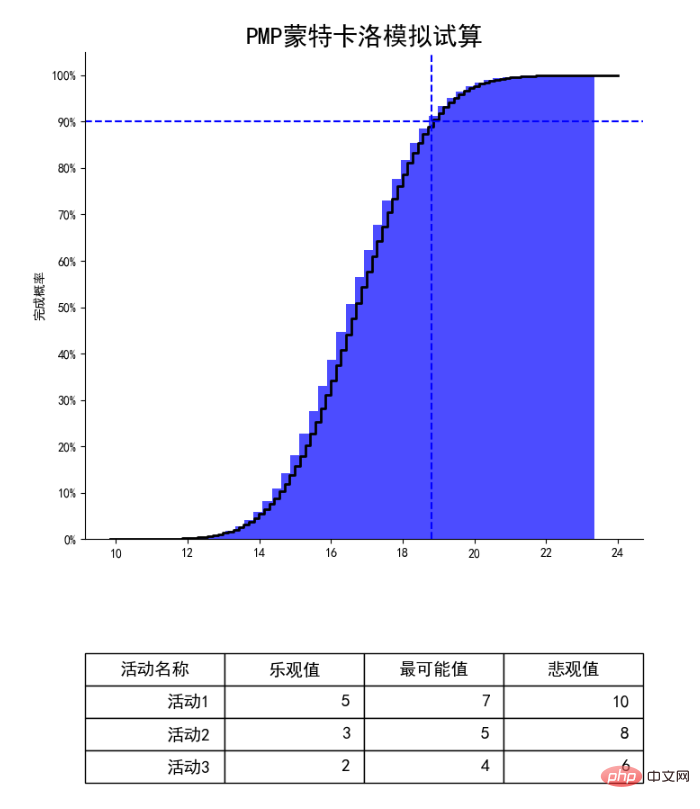
위 사진을 살펴보겠습니다. 이 사진은 활동 1, 활동 2, 활동 3의 세 가지 프로젝트 활동에 대한 몬테카를로 시뮬레이션입니다. 시뮬레이션은 세 가지 활동에 대한 3점 추정을 기반으로 합니다. 그런 다음 컴퓨터에 무작위 예산을 1,000,000번 수행하도록 요청하여 위의 그림을 얻었습니다.
위 그림에서 파란색 점선의 교차점을 예로 들어보겠습니다. 여기서 90%는 완료 확률 90%를 의미합니다. 이 지점에 해당하는 가로축은 19일에 가깝습니다. 즉, 컴퓨터 시뮬레이션을 100만 번이나 거친 셈이다. 19일 이내에 프로젝트를 완료할 확률은 90%입니다.
프로젝트를 해본 학생들은 고객이나 리더가 항상 우리가 더 빨리, 더 빨리, 더 빨리 가기를 원한다는 것을 모두 알고 있습니다. 리더는 19일은 없고 16일만 있다고 말했다. 이때 프로젝트 매니저로서 위의 차트를 통해 16일 동안 Y축에 해당하는 X축 값이 약 30% 정도 되는 것을 확인했습니다. 리더에게 물어보세요. 성공률은 30%에 불과합니다. 베팅하시겠습니까? 이것은 "과학적 운세"의 좋은 방법입니다. 핵심은 단순성과 이를 뒷받침하는 확률 이론입니다.
Python 구현
#!/usr/bin/env python
# -*- coding:utf-8 -*-
"""
#-----------------------------------------------------------------------------
# --- TDOUYA STUDIOS ---
#-----------------------------------------------------------------------------
#
# @Project : di08-tdd-cdg-python-learning
# @File : monte_carlo.py
# @Author : tianxin.xp@gmail.com
# @Date : 2023/3/12 18:22
#
# 用Python实现蒙特卡洛模拟
#
#--------------------------------------------------------------------------"""
from datetime import datetime
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.ticker import FuncFormatter, MultipleLocator
from scipy.stats import norm
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def to_percent(y, position):
# 将纵轴用百分数表示
return '{:.0f}%'.format(100 * y)
class Activity:
""" 活动类,用于表示一个项目中的活动
Attributes:
name (str): 活动名称
optimistic (float): 乐观时间
pessimistic (float): 悲观时间
most_likely (float): 最可能时间
"""
def __init__(self, name, optimistic, pessimistic, most_likely):
"""
初始化活动类
Args:
name (str): 活动名称
optimistic (float): 乐观时间
pessimistic (float): 悲观时间
most_likely (float): 最可能时间
"""
self.name = name
self.optimistic = optimistic
self.pessimistic = pessimistic
self.most_likely = most_likely
class PMP:
"""
PMP类用于进行项目管理中的相关计算:
方法:
monte_carlo_simulation : 蒙特卡洛模拟试算,包括计算项目工期、平均值、标准差、绘制积累图和概率密度曲线等功能。
"""
def __init__(self, activities):
"""
初始化PMP类,传入活动列表。
:param activities: 活动列表,包括活动名称、乐观值、最可能值和悲观值。
"""
self.activities = activities
def monte_carlo_simulation(self, n):
"""
进行蒙特卡洛模拟试算,计算项目工期、平均值、标准差、绘制积累图和概率密度曲线等。
:param n: 模拟次数。
"""
# 模拟参数和变量
t = []
for activity in self.activities:
t.append(np.random.triangular(activity.optimistic, activity.most_likely, activity.pessimistic, n))
# 计算项目工期
project_duration = sum(t)
# 计算平均值和标准差
mean_duration = np.mean(project_duration)
std_duration = np.std(project_duration)
# 绘制积累图
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(8, 10), gridspec_kw={'height_ratios': [3, 1]})
ax1.hist(project_duration, bins=50, density=True, alpha=0.7, color='blue', cumulative=True)
ax1.yaxis.set_major_locator(MultipleLocator(0.1))
ax1.yaxis.set_major_formatter(FuncFormatter(to_percent))
ax1.set_ylabel('完成概率')
ax1.set_title('PMP蒙特卡洛模拟试算', fontsize=20)
# 绘制概率密度曲线
xmin, xmax = ax1.get_xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.cdf(x, mean_duration, std_duration)
ax1.plot(x, p, 'k', linewidth=2, drawstyle='steps-post')
# 找到完成概率90%的点
x_90 = norm.ppf(0.9, mean_duration, std_duration)
# 绘制垂线
ax1.axvline(x_90, linestyle='--', color='blue')
ax1.axhline(0.9, linestyle='--', color='blue')
# 隐藏右边和上方的坐标轴线
ax1.spines['right'].set_visible(False)
ax1.spines['top'].set_visible(False)
# 添加表格
col_labels = ['活动名称', '乐观值', '最可能值', '悲观值']
cell_text = [[activity.name, activity.optimistic, activity.most_likely, activity.pessimistic] for activity in
self.activities]
table = ax2.table(cellText=cell_text, colLabels=col_labels, loc='center')
# 设置表格的字体大小和行高
table.auto_set_font_size(False)
table.set_fontsize(14)
# # 设置表格的行高为1.5倍原来的高度
for i in range(len(self.activities) + 1):
table._cells[(i, 0)].set_height(0.2)
table._cells[(i, 1)].set_height(0.2)
table._cells[(i, 2)].set_height(0.2)
table._cells[(i, 3)].set_height(0.2)
ax2.axis('off')
# 调整子图之间的间距和边距
plt.subplots_adjust(hspace=0.3, bottom=0.05)
# 保存图表
now = datetime.now().strftime('%Y%m%d%H%M%S')
plt.savefig('monte_carlo_simulation_{}.png'.format(now))
# 显示图形
plt.show()
if __name__ == '__main__':
# 模拟参数和变量
n = 1000000 # 模拟次数
# 活动的工期分布
activities = [
Activity('活动1', 5, 10, 7),
Activity('活动2', 3, 8, 5),
Activity('活动3', 2, 6, 4)
]
# 进行蒙特卡洛模拟
pmp = PMP(activities)
pmp.monte_carlo_simulation(n)위 내용은 Python에서 몬테카를로 시뮬레이션을 구현하는 방법 및 단계의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!