TSP(여행 세일즈맨 문제)를 해결하기 위해 Python을 사용하여 유전자 알고리즘을 구현하는 방법은 무엇입니까?

TSP 문제

그래서 시작하기 전에 이 TSP 문제에 대해 자세히 설명하겠습니다. 디지털 모델링을 해본 적이 있거나 지능형 최적화 또는 기계 학습에 노출된 친구들은 모두 이것을 알아야 합니다. 물론 이 기사의 보편적인 독자를 위해 우리는 이를 최대한 완벽하고 명확하게 만들기 위해 최선을 다할 것입니다. 여기서 실제로 문제를 해결할 수 있습니다.

문제는 실제로 간단합니다.

N차원 평면에서 오늘 우리가 이야기하고 있는 것은 이 2차원 평면에 많은 도시가 있습니다. 도시 도시들은 서로 연결되어 있습니다. 이제 모든 도시를 방문할 수 있는 최단 경로를 찾아야 합니다. 예를 들어 도시 A, B, C, D, E가 있습니다. 이제 도시 사이의 좌표를 알았으니, 이는 도시 사이의 거리를 아는 것과 같습니다. 이제 모든 도시 A, B, C, D, E까지 최단 경로를 만들 수 있는 시퀀스를 찾을 수 있습니다. 예를 들어 계산하면 B-->A-->C-->E-->D가 될 수 있다. 즉, 이 순서를 찾으십시오.

Enumeration

이 문제를 먼저 해결하려면 실제로 많은 솔루션이 있습니다. 직설적으로 말하면 경로의 합을 최소화할 수 있는 순서를 찾으면 됩니다. 그러면 가장 쉬운 방법은 열거입니다. 예를 들어, A를 먼저 이동시킨 다음 A에서 가장 가까운 거리가 B인지 확인한 다음 B로 이동한 다음 B에서 이동합니다. 물론 이것은 지역적 탐욕 전략이며 지역적 최적에 도달하기 쉽습니다. 그러면 이번에는 DP를 고려할 수 있습니다. 즉, 여전히 A에서 시작한다고 가정하고 2개의 도시가 다음과 같다는 것을 보장합니다. 3개 도시가 가장 짧고, 4개와 5개 도시가 가장 짧습니다. 마지막으로 B에서도 같은 일을 가정합니다. 아니면 모든 상황을 직접 열거하고 거리를 계산해 보세요. 그러나 어쨌든 도시의 수가 증가할수록 복잡성도 증가할 것이기 때문에 현시점에서 우리는 컴퓨팅이 인간의 전문 지식을 활용할 수 있는 방법을 찾아야 합니다. 나는 그것을 "실명"이라고 부릅니다.

지능형 알고리즘

이제 이 지능형 알고리즘과 이를 사용하는 이유에 대해 이야기해 보겠습니다. 이전 솔루션은 대용량 데이터에 대해 많은 계산이 필요하며 작성이 반드시 쉽지는 않다고 말했습니다. 그래서 이때 우선 TSP 문제에 대해서만 우리가 원하는 것은 시퀀스, 반복되지 않는 시퀀스입니다. 그렇다면 이때 더 간단한 해결책은 없을까요? 그리고 데이터가 충분히 크다면 가깝기만 하면 완전히 정확하고 완전히 최소한의 솔루션이 꼭 필요한 것은 아닙니다. 따라서 이때 기존 알고리즘을 사용하면 하나는 우리의 규칙에 따라서만 계산되며 표준 답이 무엇인지 실제로 알 수 없습니다. 전통적인 알고리즘 . 그러나 우리 인간에게는 '행운'이라는 것이 있습니다. 어떤 사람들은 너무 운이 좋아서 영혼에 들어오자마자 답이 혼란스러울 수도 있습니다. 따라서 우리의 지능형 알고리즘은 실제로 "원숭이"와 약간 유사합니다. 하지만 사람들은 실력에 주목합니다. 예를 들어, 경험에 따르면 긴 것 세 개와 짧은 것 한 개가 가장 짧습니다. 또는 블로거만큼 잘생긴 남자 친구를 찾을 때 이 기술을 사용할 수 있습니다. 40시리즈만 있으면 됩니다. (30개도 괜찮습니다.) 그래픽카드는 쉽게 빼낼 수 있습니다. Meng에는 기술이 필요하며 우리는 이것을 전략이라고 부릅니다.

Strategy

그래서 우리가 방금 이야기한 이 기술, 이 트릭입니다. 지능형 알고리즘에서 이 마스크는 우리의 전략 중 하나입니다. 우리의 솔루션이 더욱 합리적이 되도록 어떻게 이를 제거할 수 있습니까? 그러면 이때 백 송이의 꽃이 피기 시작합니다. 여기서는 가장 고전적인 두 가지 알고리즘을 예로 들겠습니다. 하나는 유전자 알고리즘이고 다른 하나는 입자 떼 알고리즘(PSO)입니다. 예를 들어, 그들은 자연 선택을 시뮬레이션하여 처음에 여러 솔루션과 시퀀스를 무작위로 생성한 다음 자연 선택 전략을 사용하여 솔루션을 생성하는 등의 암호 해독 전략을 사용합니다. 그런 다음 이러한 솔루션을 사용하여 새롭고 더 나은 솔루션을 찾으십시오. 이렇게 왔다 갔다 하다가 좋은 해결책을 얻었습니다. 입자군집도 비슷합니다. 이 부분은 사용하면서 자세히 설명하겠습니다.

Algorithm

이제 우리는 이 전략을 알았습니다. 알고리즘이란 실제로 이러한 전략을 구현하는 단계이며, 이것이 바로 우리의 코드, 루프 및 데이터 구조입니다. 우리는 방금 언급한 TSP와 같은 자연 선택, 수많은 솔루션을 무작위로 생성하는 방법 등을 깨달아야 합니다.

데이터 샘플

자, 여기서는 몇 가지 기본 개념에 대해 이야기했습니다. 이제 이 TSP 문제를 어떻게 표현하는지 살펴보겠습니다. 우리 입장에서는 매우 간단합니다. 여기에 14개의 도시가 있다고 가정해 보겠습니다. 이 도시에 대한 데이터는 다음과 같습니다.

    data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
                     22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
                     17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
                     21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))

이 데이터 세트를 나중에 테스트에 사용할 예정이며 이제 14개의 도시가 있습니다.

그럼 솔루션을 시작하겠습니다

유전자 알고리즘

좋아요, 그럼 우리의 유전자 알고리즘이 무엇인지 이야기한 다음 이를 사용하여 이 TSP 문제를 해결하겠습니다.

이제 우리의 유전자 알고리즘이 어떻게 속는지 살펴보겠습니다.

算法流程

遗传算法其实是在用计算机模拟我们的物种进化。其实更加通俗的说法是筛选，这个就和我们袁老爷爷种植水稻一样。有些个体发育良好，有些个体发育不好，那么我就先筛选出发育好的，然后让他们去繁衍后代，然后再筛选，最后得到高产水稻。其实也和我们社会一样，不努力就木有女朋友就不能保留自己的基因，然后剩下的人就是那些优秀的人和富二代的基因，这就是现实呀。所以得好好学习，天天向上！

那么回到主题，我们的遗传算法就是在模拟这一个过程，模拟一个物竞天择的过程。

所以在我们的算法里面也是分为几大块

繁殖

首先我们的种群需要先繁殖。这样才能不断产生优良基于，那么对应我们的算法，假设我们需要求取

Y = np.sin(10 * x) * x + np.cos(2 * x) * x

的最大值（在一个范围内）那么我们的个体就是一组（X1）的解。好的个体就会被保留，不好的就会被pass，选择标准就是我们的函数 Y 。那么问题来了如何模拟这个过程？我们都知道在繁殖后代的时候我们是通过DNA来保留我们的基因信息，在这个过程当中，父母的DNA交互，并且在这个过程当中会产生变异，这样一来，父母双方的优秀基于会被保存，并且产生的变异有可能诞生更加优秀的后代。

所以接下来我们需要模拟我们的ＤＮＡ，进行交叉和变异。

交叉

这个交叉过程和我们的生物其实很像，当然我们在我们的计算机里面对于数字我们可以将其转化为二进制，当做我们的DNA

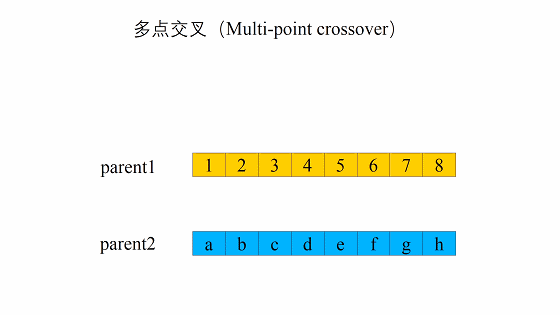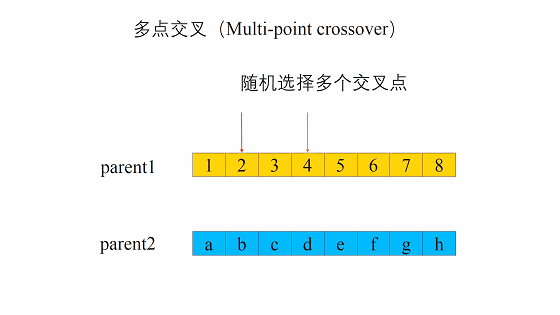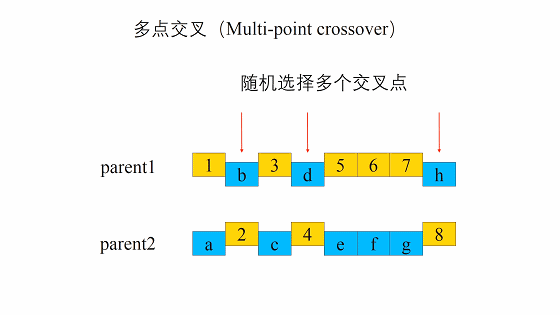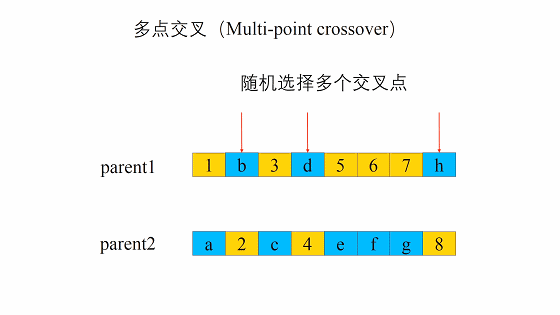
交叉的方式有很多，我们这边选择这一个，进行交叉。

变异

那这个在我们这里就更加简单了

我们只需要在交叉之后，再随机选择几个位置进行改变值就可以了。当然变异的概率是很小的，并且是随机的，这一点要注意。并且由于变异是随机的，所以不排除生成比原来还更加糟糕的个体。

选择

最后我们按照一定的规则去筛选这个些个体就可以了，然后淘汰原来的个体。那么在我们的计算机里面是使用了两个东西，首先我们要把原来二进制的玩意，给转化为我们原来的十进制然后带入我们的函数运算，然后保存起来，之后再每一轮统一筛选一下就好了。

逆转

这个咋说呢，说好听点叫逆转，难听点就算，对于一些新的生成的不好的解，我们是要舍弃的。

代码

那么这部分用代码描述的话就是这样的：

import numpy as np
import matplotlib.pyplot as plt
Population_Size = 100
Iteration_Number = 200
Cross_Rate = 0.8
Mutation_Rate = 0.003
Dna_Size = 10
X_Range=[0,5]
def F(x):
    '''
    目标函数，需要被优化的函数
    :param x:
    :return:
    '''
    return np.sin(10 * x) * x + np.cos(2 * x) * x
def CrossOver(Parent,PopSpace):
    '''
    交叉DNA，我们直接在种群里面选择一个交配
    然后就生出孩子了
    :param parent:
    :param PopSpace:
    :return:
    '''
    if(np.random.rand()) < Cross_Rate:
        cross_place = np.random.randint(0, 2, size=Dna_Size).astype(np.bool)
        cross_one = np.random.randint(0, Population_Size, size=1) #选择一位男/女士交配
        Parent[cross_place] = PopSpace[cross_one,cross_place]
    return Parent
def Mutate(Child):
    &#39;&#39;&#39;
    变异
    :param Child:
    :return:
    &#39;&#39;&#39;
    for point in range(Dna_Size):
        if np.random.rand() < Mutation_Rate:
            Child[point] = 1 if Child[point] == 0 else 0
    return Child
def TranslateDNA(PopSpace):
    &#39;&#39;&#39;
    把二进制转化为十进制方便计算
    :param PopSpace:
    :return:
    &#39;&#39;&#39;
    return PopSpace.dot(2 ** np.arange(Dna_Size)[::-1]) / float(2 ** Dna_Size - 1) * X_Range[1]
def Fitness(pred):
    &#39;&#39;&#39;
    这个其实是对我们得到的F(x)进行换算，其实就是选择的时候
    的概率，我们需要处理负数，因为概率不能为负数呀
    pred 这是一个二维矩阵
    :param pred:
    :return:
    &#39;&#39;&#39;
    return pred + 1e-3 - np.min(pred)
def Select(PopSpace,Fitness):
    &#39;&#39;&#39;
    选择
    :param PopSpace:
    :param Fitness:
    :return:
    &#39;&#39;&#39;
    &#39;&#39;&#39;
    这里注意的是，我们先按照权重去选择我们的优良个体，所以我们这里选择的时候允许重复的元素出现
    之后我们就可以去掉这些重复的元素，这样才能实现保留良种去除劣种。100--》70（假设有30个重复）
    如果不允许重复的话，那你相当于没有筛选
    &#39;&#39;&#39;
    Better_Ones = np.random.choice(np.arange(Population_Size), size=Population_Size, replace=True,
                           p=Fitness / Fitness.sum())
    # np.unique(Better_Ones) #这个是我后面加的
    return PopSpace[Better_Ones]
if __name__ == &#39;__main__&#39;:
    PopSpace = np.random.randint(2, size=(Population_Size, Dna_Size))  # initialize the PopSpace DNA
    plt.ion() 
    x = np.linspace(X_Range, 200)
    # plt.plot(x, F(x))
    plt.xticks([0,10])
    plt.yticks([0,10])
    for _ in range(Iteration_Number):
        F_values = F(TranslateDNA(PopSpace))  
        # something about plotting
        if &#39;sca&#39; in globals():
            sca.remove()
        sca = plt.scatter(TranslateDNA(PopSpace), F_values, s=200, lw=0, c=&#39;red&#39;, alpha=0.5)
        plt.pause(0.05)
        # GA part (evolution)
        fitness = Fitness(F_values)
        print("Most fitted DNA: ", PopSpace[np.argmax(fitness)])
        PopSpace = Select(PopSpace, fitness)
        PopSpace_copy = PopSpace.copy()
        for parent in PopSpace:
            child = CrossOver(parent, PopSpace_copy)
            child = Mutate(child)
            parent[:] = child
    plt.ioff()
    plt.show()

这个代码是以前写的，逆转没有写上（下面的有）

TSP遗传算法

ok,刚刚的例子是拿的解方程，也就是说是一个连续问题吧，当然那个连续处理的话并不是很好，只是一个演示。那么我们这个的话其实类似的。首先我们的ＤＮＡ，是城市的路径，也就是A-B-C-D等等，当然我们用下标表示城市。

种群表示

首先我们确定了使用城市的序号作为我们的个体DNA，例如咱们种群大小为100，有ＡＢＣＤ四个城市，那么他就是这样的，我们先随机生成种群，长这个样：

1 2 3 4
2 3 4 5
3 2 1 4
...

那个1,2,3,4是ABCD的序号。

交叉与变异

这里面的话，值得一提的就是，由于暂定城市需要是不能重复的，且必须是完整的，所以如果像刚刚那样进行交叉或者变异的话，那么实际上会出点问题，我们不允许出现重复，且必须完整，对于我们的DNA，也就是咱们瞎蒙的个体。

代码

由于咱们每一步在代码里面都有注释，所以的话咱们在这里就不再进行复述了。

from math import floor
import numpy as np
import matplotlib.pyplot as plt
class Gena_TSP(object):
    """
    使用遗传算法解决TSP问题
    """
    def __init__(self, data, maxgen=200,
                 size_pop=200, cross_prob=0.9,
                 pmuta_prob=0.01, select_prob=0.8
                 ):
        self.maxgen = maxgen            # 最大迭代次数
        self.size_pop = size_pop        # 群体个数，（一次性瞎蒙多少个解）
        self.cross_prob = cross_prob    # 交叉概率
        self.pmuta_prob = pmuta_prob    # 变异概率
        self.select_prob = select_prob  # 选择概率
        self.data = data        # 城市的坐标数据
        self.num = len(data)    # 有多少个城市，对应多少个坐标，对应染色体的长度（我们的解叫做染色体）
        """
        计算城市的距离，我们用矩阵表示城市间的距离
        """
        self.__matrix_distance = self.__matrix_dis()
        self.select_num = int(self.size_pop * self.select_prob)
        # 通过选择概率确定子代的选择个数
        """
        初始化子代和父代种群，两者相互交替
        """
        self.parent = np.array([0] * self.size_pop * self.num).reshape(self.size_pop, self.num)
        self.child = np.array([0] * self.select_num * self.num).reshape(self.select_num, self.num)
        """
        负责计算每一个个体的（瞎蒙的解）最后需要多少距离
        """
        self.fitness = np.zeros(self.size_pop)
        self.best_fit = []
        self.best_path = []
        # 保存每一步的群体的最优路径和距离
    def __matrix_dis(self):
        """
        计算14个城市的距离，将这些距离用矩阵存起来
        :return: 
        """
        res = np.zeros((self.num, self.num))
        for i in range(self.num):
            for j in range(i + 1, self.num):
                res[i, j] = np.linalg.norm(self.data[i, :] - self.data[j, :])
                res[j, i] = res[i, j]
        return res
    def rand_parent(self):
        """
        初始化种群
        :return:
        """
        rand_ch = np.array(range(self.num))
        for i in range(self.size_pop):
            np.random.shuffle(rand_ch)
            self.parent[i, :] = rand_ch
            self.fitness[i] = self.comp_fit(rand_ch)
    def comp_fit(self, one_path):
        """
        计算，咱们这个路径的长度，例如A-B-C-D
        :param one_path:
        :return:
        """
        res = 0
        for i in range(self.num - 1):
            res += self.__matrix_distance[one_path[i], one_path[i + 1]]
        res += self.__matrix_distance[one_path[-1], one_path[0]]
        return res
    def out_path(self, one_path):
        """
        输出我们的路径顺序
        :param one_path:
        :return:
        """
        res = str(one_path[0] + 1) + '-->'
        for i in range(1, self.num):
            res += str(one_path[i] + 1) + '-->'
        res += str(one_path[0] + 1) + '\n'
        print(res)
    def Select(self):
        """
        通过我们的这个计算的距离来计算出概率，也就是当前这些个体DNA也就瞎蒙的解
        之后我们在通过概率去选择个体，放到child里面
        :return:
        """
        fit = 1. / (self.fitness)  # 适应度函数
        cumsum_fit = np.cumsum(fit)
        pick = cumsum_fit[-1] / self.select_num * (np.random.rand() + np.array(range(self.select_num)))
        i, j = 0, 0
        index = []
        while i < self.size_pop and j < self.select_num:
            if cumsum_fit[i] >= pick[j]:
                index.append(i)
                j += 1
            else:
                i += 1
        self.child = self.parent[index, :]
    def Cross(self):
        """
        模仿DNA交叉嘛，就是交换两个瞎蒙的解的部分的解例如
        A-B-C-D
        C-D-A-B
        我们选几个交叉例如这样
        A-D-C-B
        1,3号交换了位置，当然这里注意可不能重复啊
        :return:
        """
        if self.select_num % 2 == 0:
            num = range(0, self.select_num, 2)
        else:
            num = range(0, self.select_num - 1, 2)
        for i in num:
            if self.cross_prob >= np.random.rand():
                self.child[i, :], self.child[i + 1, :] = self.intercross(self.child[i, :],
                                                                             self.child[i + 1, :])
    def intercross(self, ind_a, ind_b):
        """
        这个是我们两两交叉的具体实现
        :param ind_a:
        :param ind_b:
        :return:
        """
        r1 = np.random.randint(self.num)
        r2 = np.random.randint(self.num)
        while r2 == r1:
            r2 = np.random.randint(self.num)
        left, right = min(r1, r2), max(r1, r2)
        ind_a1 = ind_a.copy()
        ind_b1 = ind_b.copy()
        for i in range(left, right + 1):
            ind_a2 = ind_a.copy()
            ind_b2 = ind_b.copy()
            ind_a[i] = ind_b1[i]
            ind_b[i] = ind_a1[i]
            x = np.argwhere(ind_a == ind_a[i])
            y = np.argwhere(ind_b == ind_b[i])
            if len(x) == 2:
                ind_a[x[x != i]] = ind_a2[i]
            if len(y) == 2:
                ind_b[y[y != i]] = ind_b2[i]
        return ind_a, ind_b
    def Mutation(self):
        """
        之后是变异模块，这个就是按照某个概率，去替换瞎蒙的解里面的其中几个元素。
        :return:
        """
        for i in range(self.select_num):
            if np.random.rand() <= self.cross_prob:
                r1 = np.random.randint(self.num)
                r2 = np.random.randint(self.num)
                while r2 == r1:
                    r2 = np.random.randint(self.num)
                self.child[i, [r1, r2]] = self.child[i, [r2, r1]]
    def Reverse(self):
        """
        近化逆转，就是说下一次瞎蒙的解如果没有更好的话就不进入下一代，同时也是随机选择一个部分的
        我们不是一次性全部替换
        :return: 
        """
        for i in range(self.select_num):
            r1 = np.random.randint(self.num)
            r2 = np.random.randint(self.num)
            while r2 == r1:
                r2 = np.random.randint(self.num)
            left, right = min(r1, r2), max(r1, r2)
            sel = self.child[i, :].copy()
            sel[left:right + 1] = self.child[i, left:right + 1][::-1]
            if self.comp_fit(sel) < self.comp_fit(self.child[i, :]):
                self.child[i, :] = sel
    def Born(self):
        """
        替换，子代变成新的父代
        :return:
        """
        index = np.argsort(self.fitness)[::-1]
        self.parent[index[:self.select_num], :] = self.child
def main(data):
    Path_short = Gena_TSP(data)     # 根据位置坐标，生成一个遗传算法类
    Path_short.rand_parent()        # 初始化父类
    ## 绘制初始化的路径图
    fig, ax = plt.subplots()
    x = data[:, 0]
    y = data[:, 1]
    ax.scatter(x, y, linewidths=0.1)
    for i, txt in enumerate(range(1, len(data) + 1)):
        ax.annotate(txt, (x[i], y[i]))
    res0 = Path_short.parent[0]
    x0 = x[res0]
    y0 = y[res0]
    for i in range(len(data) - 1):
        plt.quiver(x0[i], y0[i], x0[i + 1] - x0[i], y0[i + 1] - y0[i], color=&#39;r&#39;, width=0.005, angles=&#39;xy&#39;, scale=1,
                   scale_units=&#39;xy&#39;)
    plt.quiver(x0[-1], y0[-1], x0[0] - x0[-1], y0[0] - y0[-1], color=&#39;r&#39;, width=0.005, angles=&#39;xy&#39;, scale=1,
               scale_units=&#39;xy&#39;)
    plt.show()
    print(&#39;初始染色体的路程: &#39; + str(Path_short.fitness[0]))
    # 循环迭代遗传过程
    for i in range(Path_short.maxgen):
        Path_short.Select()     # 选择子代
        Path_short.Cross()      # 交叉
        Path_short.Mutation()   # 变异
        Path_short.Reverse()    # 进化逆转
        Path_short.Born()      # 子代插入
        # 重新计算新群体的距离值
        for j in range(Path_short.size_pop):
            Path_short.fitness[j] = Path_short.comp_fit(Path_short.parent[j, :])
        index = Path_short.fitness.argmin()
        if (i + 1) % 50 == 0:
            print(&#39;第&#39; + str(i + 1) + &#39;步后的最短的路程: &#39; + str(Path_short.fitness[index]))
            print(&#39;第&#39; + str(i + 1) + &#39;步后的最优路径:&#39;)
            Path_short.out_path(Path_short.parent[index, :])  # 显示每一步的最优路径
        # 存储每一步的最优路径及距离
        Path_short.best_fit.append(Path_short.fitness[index])
        Path_short.best_path.append(Path_short.parent[index, :])
    return Path_short  # 返回遗传算法结果类
if __name__ == &#39;__main__&#39;:
    data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
                     22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
                     17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
                     21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))
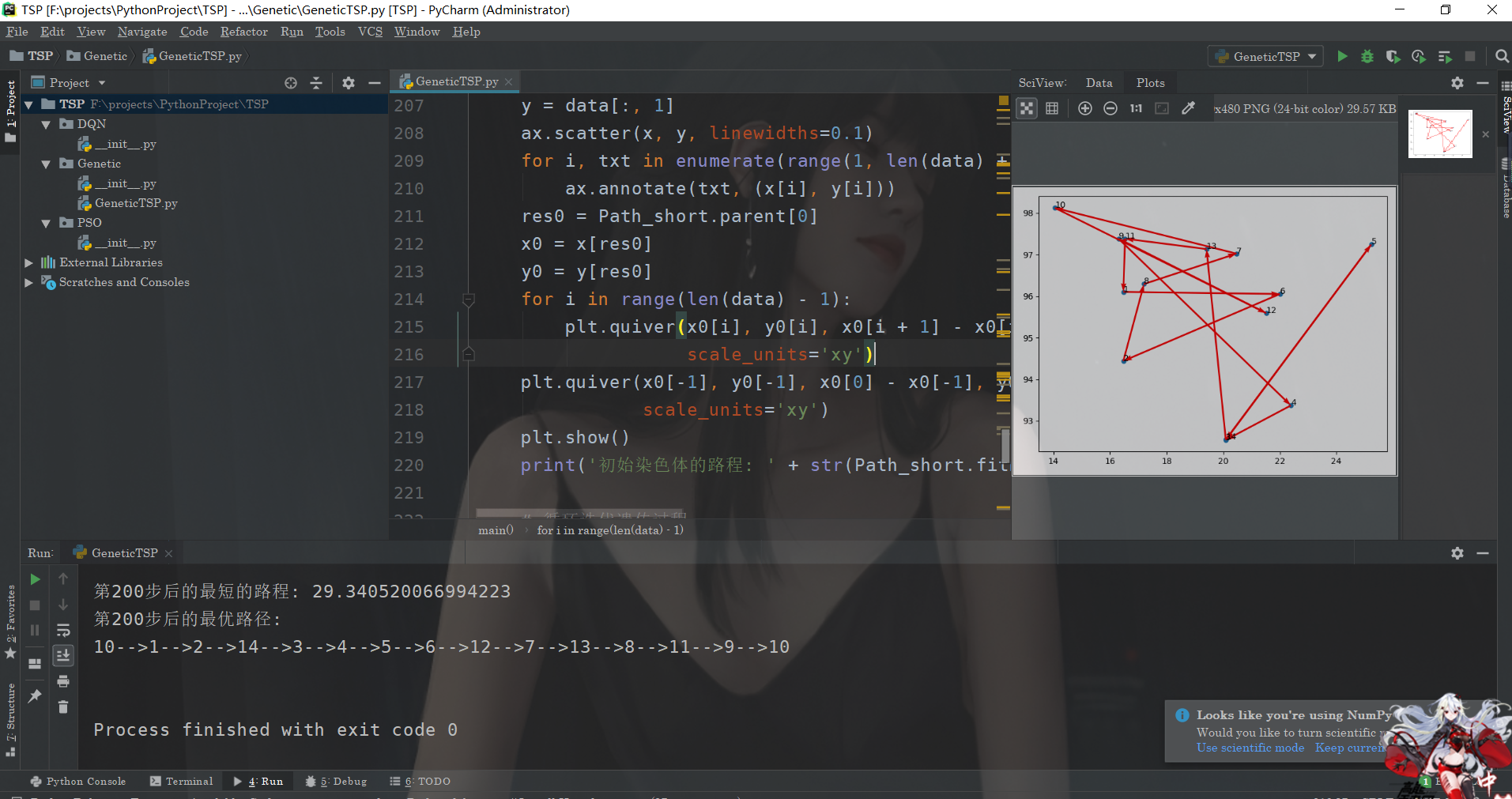
    main(data)

运行结果

ok,我们来看看运行的结果：

위 내용은 TSP(여행 세일즈맨 문제)를 해결하기 위해 Python을 사용하여 유전자 알고리즘을 구현하는 방법은 무엇입니까?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!