Chicken Swarm Optimization, 줄여서 CSO(Chicken Swarm Optimization)는 소위 생체공학에 대한 배경 지식을 갖고 있지만 본질적으로 입자 떼 알고리즘의 변형입니다.
간단히 말해서 입자 떼는 입자의 그룹입니다. 각 입자는 고유한 위치와 속도를 가지며, 이 두 가지 규칙을 제외하면 입자는 완전히 동일합니다. 위치와 속도만 빼고요.
물론, 입자 떼 알고리즘 자체도 생체 공학적 배경을 갖고 있다고 합니다. 이는 먹이를 찾는 새 떼에서 영감을 받았다고 합니다. 이는 물론 동등한 입자들이 회전하는 것에 지나지 않습니다. 동등한 새들의 그룹으로.
닭 무리 알고리즘은 이러한 입자 또는 새에 서로 다른 정체성 특성을 추가하여 더 이상 서로 동등하지 않습니다.
닭 떼에는 수탉, 암탉, 병아리라는 세 가지 클래스가 있습니다. 각 닭은 고유한 위치와 속도를 가지고 있습니다. 하지만 차이점은
수탉이 가장 위엄이 있다는 것입니다. 원칙적으로는 마음대로 돌아다닐 수 있지만 때로는 다른 수탉을 발견하면 먹이를 움켜쥘 수도 있습니다. 다른 수탉을 무작위로 선택하는 것과 같습니다. 그 위치는 영향을 미칩니다.
암탉은 한편으로는 수탉의 리더십을 받아들여야 하고, 다른 한편으로는 먹이를 놓고 다른 암탉과 경쟁해야 합니다.
병아리가 가장 불만스럽습니다. 근심 걱정 없이 암탉을 따라가세요.
위치 관계가 변화함에 따라 암탉과 병아리는 점차 원래의 리더를 잊어버릴 수 있으며, 이는 개체군 관계가 바뀔 수 있음을 의미합니다.
우선 닭 클래스를 구현해야 합니다. 닭에는 위치와 카테고리라는 두 가지 기본 속성이 있습니다.
import numpy as np
from random import gauss, random
randint = np.random.randint
uniRand = np.random.uniform
class Chicken:
def __init__(self, N, xRange, order=0, kind=0):
# 生成(N)维参数
self.x = uniRand(*xRange, (N,))
self.best = np.inf
self.xBest = np.zeros((N,))
self.kind = kind # 鸡的类别
self.order = order # 鸡的编号
# 设置自己的首领公鸡
def setCock(self, i):
self.cock = i
# 设置自己的监护母鸡
def setHen(self, i):
self.hen = i종류는 수탉, 암탉, 병아리의 세 가지 범주로 나뉩니다. 그중 암탉마다 알파 수탉이 있고, 병아리마다 수호암탉이 있습니다.
주문은 닭떼에 있는 이 닭의 숫자로 닭떼에 주로 반영됩니다.
닭 무리와 입자 떼 사이에는 큰 차이가 있습니다. 최종 분석에서 후자에는 무리가 하나 뿐이지만 닭 무리에서는 각 수탉이 자신의 암탉과 병아리를 가지고 있으며 이는 소그룹에 해당합니다. . 하지만 닭 간의 관계는 닭 자체에 의존하지 않으므로 닭 떼에서 구현해야 합니다
randint = np.random.randint
class Swarm:
# cNum 鸡数，是三个元素的列表，分别是公鸡、母鸡和小鸡数
# N参数维度
def __init__(self, cNum, N, xRange):
self.initCs(cNum, N, xRange)
self.bestCS = deepcopy(self.cs) #最佳鸡群
self.best = np.inf #全局最优值
self.xBest = np.zeros((N,)) #全局最优参数
self.N = N
def initCs(self, cNum, N, xRange, vRange):
self.cs = []
self.cNum = cNum
self.cocks = np.arange(cNum[0]) # 公鸡编号
self.hens = np.arange(cNum[0], cNum[0]+cNum[1]) #母鸡编号
self.chicks = np.arange(cNum[0]+cNum[1], np.sum(cNum)) #小鸡编号
kinds = np.repeat([0,1,2], cNum)
for i in range(sum(cNum)):
self.cs.append(Chicken(N,xRange, vRange, i, kinds[i]))
if kinds[i] > 0:
cock = randint(0, cNum[0])
self.cs[i].setCock(cock)
if kinds[i] > 1:
hen = randint(cNum[0], cNum[0]+cNum[1])
self.cs[i].setHen(hen)그 중 initCs는 닭 떼를 초기화하는 기능인데, 그 중 닭의 리더인 암탉이, 닭의 수호자인 수탉 암탉은 모두 무작위로 생성됩니다.
다음 단계는 알고리즘의 핵심 부분입니다. 다양한 닭은 서로 다른 업데이트 규칙을 따라야 합니다. 그 중에서 수탉이 가장 멋지고, 그 다음 위치는 자신과 무작위로 선택된 다른 수탉에만 달려 있습니다.
Cock
현재 수탉의 수는 i이고 무작위로 선택된 수탉의 수는 j, j≠i라는 점을 기억하세요. 그러면 i번째 수탉의 위치 업데이트 방법은
x입니다. i(t+1) =xi(t)⋅(1+r)
여기서, r은 정규분포를 통해 생성된 난수로, 1∼N(0,σ 2), 여기서 σ 2는
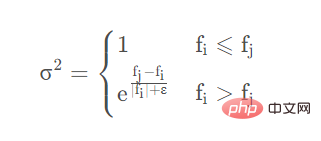
입니다. 여기서 f는 일반적으로 적응 인자라고 하며, 이는 검색할 함수에 특정 닭을 채워서 얻은 값과 같습니다. 예를 들어 y=2의 최소값을 검색하려면 닭의 현재 위치가 1.5라면 f=1.52=2.25가 됩니다. ε은 0으로 나누는 오류를 방지하는 소량입니다.
하지만 위의 모든 x는 스칼라가 아니라 배열을 나타낸다는 점에 유의해야 합니다.
파이썬 구현은
# 写在Swarm类中
def cockStep(self):
for i in self.cocks:
# 第j只公鸡
j = np.random.randint(self.cNum[0])
if j==i:
j = (j+1) % self.cNum[0]
# 第i只公鸡
ci = self.cs[i]
# 第j只公鸡
cj = self.cs[self.cocks[j]]
sigma = 1 if cj.best > ci.best else np.exp(
(cj.best-ci.best)/(np.abs(ci.best)+1e-15))
ci.x *= 1 + gauss(0, sigma)Hen
입니다. 현재 암탉 번호가 i라고 가정합니다. 이 암탉은 리더 수탉을 따라갈 뿐만 아니라 다른 암탉과도 먹이를 놓고 경쟁해야 합니다.
xi(t+1)=xi(t)+k1r1(xc−xi)+k2r2( xj− k1, k
2는 계수이며 업데이트 로직은 rooster와 동일합니다. fi가 커지면 로 표현됩니다. 코드는
def henStep(self):
nGuarder = self.cNum[0] + self.cNum[1] - 2
for i in self.hens:
guarders = list(self.cocks) + list(self.hens)
c = self.cs[i].cock #首领公鸡
guarders.remove(i)
guarders.remove(c)
# 随机生成另一只监护鸡
j = guarders[np.random.randint(nGuarder)]
ci = self.cs[i]
cj = self.cs[j]
cc = self.cs[c]
k1, k2 = random(), random()
if cc.best > ci.best:
k1 *= np.exp((ci.best-cc.best)/(np.abs(ci.best)+1e-15))
if cj.best < ci.best:
k2 *= np.exp(cj.best-ci.best)
ci.x += k1*(cc.x-ci.x)+k2*(cj.x-ci.x) 
마지막은 병아리가 암탉 주변에서 먹이를 찾는 업데이트 로직입니다. 업데이트 로직은
x
i(t+1)=xi(t)+r(입니다. x
h( t)− 생명은 생명보다 높습니다. 자연에서는 서열이 강조되지만 닭 무리 알고리즘에서는 확실히 힘이 강조됩니다. 닭이 운이 좋고 수탉보다 더 나은 최적화 결과를 얻으면 닭은 수탉으로 진화합니다.
즉, 가끔씩 무리에 있는 닭의 정체성이 재배열됩니다. 최적화 효과가 가장 좋은 쪽은 리더 수탉이고, 나쁜 쪽은 수호암탉이고, 가장 나쁜 쪽은 오직 수탉뿐입니다. 병아리가 되십시오. 其基本逻辑是，输入一个待优化func，通过将每只鸡的位置x带入到这个函数中，得到一个判定值，最后通过这个判定值，来不断更新鸡群。 除了这个函数之外，还需要输入一些其他参数，比如整个鸡群算法的迭代次数，以及鸡群更新的频次等等 其中，printBest可以将当前最佳结果打印出来，其形式为 算法完成之后，当然要找个函数测试一下，测试函数为 测试结果如下 已经迭代4次，最佳优化结果为-5.793762423022024，参数为： 위 내용은 Python에서 닭 떼 알고리즘을 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!def chickStep(self):
for i in self.chicks:
ci = self.cs[i]
ci.x += 2*random()*(self.cs[ci.hen].x-ci.x)# func为待优化函数
# N为迭代次数
# T为鸡群更新周期
def optimize(self, func, N, T, msgT):
for n in range(N):
# 计算优化参数
for c in self.cs:
c.best = func(c.x)
# 分别更新公鸡、母鸡和小鸡
self.cockStep()
self.henStep()
self.chickStep()
if (n+1)%T == 0:
self.update() #每T次更新一次种群
self.printBest(n)
self.printBest(n)def printBest(self,n):
fitness = [c.best for c in self.cs]
best = np.min(fitness)
ind = np.where(fitness==best)[0]
msg = f"已经迭代{n}次，最佳优化结果为{np.min(fitness)}，参数为：\n"
msg += ", ".join([f"{x:.6f}" for x in self.cs[ind].x])
print(msg)测试
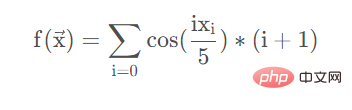
def test(xs):
_sum = 0.0
for i in range(len(xs)):
_sum = _sum + np.cos((xs[i]*i)/5)*(i+1)
return _sum
if __name__ == "__main__":
cNum = [15,20,100]
s = Swarm(cNum, 5, (-5,5))
s.optimize(test, 20, 5)
-6.599526, 3.117137, 5.959538, 7.225785, 5.204990
已经迭代9次，最佳优化结果为-10.61594651972434，参数为：
-7.003724, -5.589730, 0.981409, 12.920325, -19.006112
已经迭代14次，最佳优化结果为-9.143596747975293，参数为：
5.388234, -3.714421, -5.254391, -5.216215, -6.079223
已经迭代19次，最佳优化结果为-11.097888385616995，参数为：
-9.156244, -5.914600, -5.960154, 4.550833, 4.127889
已经迭代19次，最佳优化结果为-11.097888385616995，参数为：
-9.156244, -5.914600, -5.960154, 4.550833, 4.127889
![[웹 프런트엔드] Node.js 빠른 시작](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
