AI는 다시 한 번 수학 세계에 참여하고 새로운 DSP 방법은 기계 증명의 성공률을 두 배로 늘립니다.
수학적 정리를 자동으로 증명하는 것은 인공지능의 본래 의도이며 항상 문제가 되어 왔습니다. 지금까지 인간 수학자들은 수학을 작성하는 데 두 가지 다른 방법을 사용했습니다.
첫 번째 방법은 모두에게 익숙한 방법으로, 자연어를 사용하여 수학적 증명을 기술하는 것입니다. 수학 교과서, 수학 논문 등 대부분의 수학은 이런 방식으로 작성됩니다.
두 번째 유형은 형식수학이라고 합니다. 이것은 수학적 증명을 확인하기 위해 지난 반세기 동안 컴퓨터 과학자들이 만든 도구입니다.
요즘 컴퓨터를 사용하여 수학적 증명을 검증할 수 있는 것처럼 보이지만 수학자가 사용하는 수학적 표기법과 문자 텍스트의 혼합을 처리할 수 없는 특별히 고안된 증명 언어를 통해서만 그렇게 할 수 있습니다. 자연어로 작성된 수학 문제를 컴퓨터가 더 쉽게 해결할 수 있도록 형식 코드로 변환하면 수학의 새로운 발견을 탐색할 수 있는 기계를 구축하는 데 도움이 될 수 있습니다. 이 과정을 형식화라고 하며, 자동 형식화는 수학을 자연어에서 형식 언어로 자동 번역하는 작업을 의미합니다.
공식 증명의 자동화는 어려운 작업이며 딥 러닝 방법은 주로 공식 데이터의 부족으로 인해 이 분야에서 아직 큰 성공을 거두지 못했습니다. 실제로 형식적인 증명 자체는 매우 어렵고 소수의 전문가만이 할 수 있기 때문에 대규모 주석 작업은 비현실적입니다. 가장 큰 형식 증명 자료는 Isabelle 코드(Paulson, 1994)로 작성되었으며 크기는 0.6GB 미만으로 비전 또는 자연어 처리에서 일반적으로 사용되는 데이터 세트보다 훨씬 작습니다. 형식 증명의 부족 문제를 해결하기 위해 이전 연구에서는 합성 데이터, 자기 지도 학습 또는 강화 학습을 사용하여 추가 형식 교육 데이터를 합성하는 것을 제안했습니다. 이러한 방법은 데이터 부족을 어느 정도 완화하지만, 수작업으로 작성된 수많은 수학적 증명을 완전히 활용할 수는 없습니다.
언어 모델 Minerva를 예로 들어보겠습니다. 충분한 데이터로 훈련한 후 우리는 수학 능력이 매우 뛰어나고 고등학교 수학 시험에서 평균보다 높은 점수를 얻을 수 있다는 것을 발견했습니다. 그러나 이러한 언어 모델에도 단점이 있습니다. 모방만 할 수 있을 뿐, 수학을 향상시키기 위해 독립적으로 훈련할 수는 없습니다. 형식 증명 시스템은 훈련 환경을 제공하지만 형식 수학에 대한 데이터는 거의 없습니다.
공식 수학과 달리 비공식 수학 데이터는 풍부하고 널리 사용 가능합니다. 최근 비공식 수학적 데이터에 대해 훈련된 대규모 언어 모델은 인상적인 정량적 추론 능력을 보여주었습니다. 그러나 종종 잘못된 증명을 생성하며 이러한 증명에서 잘못된 추론을 자동으로 감지하는 것은 어렵습니다.
최근 연구에서 Google의 Yuhuai Tony Wu와 같은 연구자들은 비공식 수학적 증명을 형식 증명의 경우 형식 증명이 제공하는 논리적 엄격함과 시스템과 대량의 비공식 데이터.

문서 링크: https://arxiv.org/pdf/2210.12283.pdf
올해 초 Wu Yuhuai와 여러 협력자들은 OpenAI Codex의 신경망을 사용하여 자동 수행을 수행했습니다. 공식화 작업을 수행하고 대규모 언어 모델을 사용하여 비공식 진술을 공식 진술로 자동 변환하는 타당성을 입증합니다. DSP는 한 단계 더 나아가 대규모 언어 모델을 사용하여 비공식 증명에서 공식 증명 스케치를 생성합니다. 증명 스케치는 대화형 정리 증명과 같은 공식 시스템으로 해석될 수 있는 높은 수준의 추론 단계로 구성됩니다. 이는 정당화되지 않은 중간 추측의 시퀀스를 포함한다는 점에서 완전한 공식 증명과 다릅니다. DSP의 마지막 단계에서는 모든 중간 추측을 증명하기 위해 자동 검증기를 사용하여 형식 증명 스케치를 완전한 형식 증명으로 정교화합니다.
Wu Yuhuai가 말했습니다: 이제 우리는 LLM이 생성한 비공식 증명을 검증된 공식 증명으로 변환할 수 있음을 보여줍니다!
방법
방법 섹션에서는 비공식 증명을 활용하여 자동화된 형식 정리 증명자를 위한 증명 스케치를 안내하는 형식 증명 자동화를 위한 DSP 접근 방식을 설명합니다. 여기서는 각 문제에 문제를 설명하는 비공식적 명제와 공식적 명제가 있다고 가정합니다. 전체 파이프라인은 세 단계로 구성됩니다(그림 1 참조).
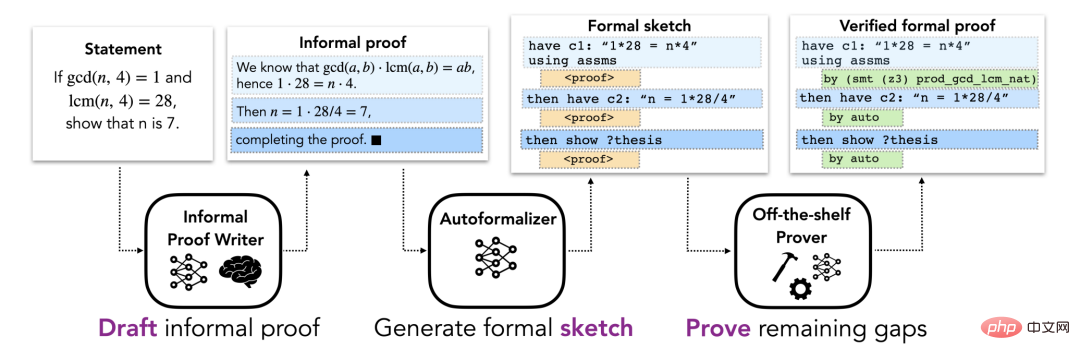
그림 1.
비공식 증명 초안 작성
자연스러운 수학적 언어 설명을 기반으로 문제에 대한 비공식 형식을 찾는 것을 포함하는 DSP 방법의 초기 단계(아마도 LATEX을 사용하여) 증명. 결과로 나온 비공식 증명은 후속 단계의 초안으로 처리됩니다. 수학 교과서에는 일반적으로 정리의 증명이 제공되지만 때로는 누락되거나 불완전한 경우도 있습니다. 따라서 연구자들은 비공식적 증거의 유무에 해당하는 두 가지 상황을 고려했습니다.
첫 번째 경우, 연구자는 기존 수학 이론의 형식적 실천에서 전형적인 상황인 "실제" 비공식 증명(즉, 인간이 작성한 증명)이 있다고 가정합니다. 두 번째 경우, 연구자들은 실제 비공식 증거가 제공되지 않는다는 보다 일반적인 가정을 하고 비공식 수학적 데이터에 대해 훈련된 대규모 언어 모델을 사용하여 증거 후보 초안을 작성합니다. 언어 모델은 인간 증명에 대한 의존성을 제거하고 각 문제에 대한 여러 대체 솔루션을 생성할 수 있습니다. 이러한 증명의 정확성을 자동으로 확인하는 쉬운 방법은 없지만 비공식 증명은 좋은 형식 증명 스케치를 생성하는 다음 단계에서만 유용하면 됩니다.
비공식 증명을 공식 스케치로 매핑
정식 증명 스케치는 솔루션의 구조를 인코딩하고 하위 수준 세부 정보는 제쳐두세요. 직관적으로 이것은 높은 수준의 추측 진술을 개괄적으로 설명하는 부분 증명입니다. 그림 2는 교정 스케치의 구체적인 예입니다. 비공식 증명은 종종 낮은 수준의 세부 사항을 제쳐두지만, 이러한 세부 사항은 형식 증명에서 제외될 수 없으므로 비공식 증명을 형식 증명으로 직접 전환하는 것이 어렵습니다. 대신, 이 논문에서는 동일한 상위 수준 구조를 공유하는 공식 증명 스케치에 비공식 증명을 매핑하는 것을 제안합니다. 교정 스케치에서 누락된 낮은 수준의 세부 사항은 자동 교정기로 채워질 수 있습니다. 대규모 비공식-정형 병렬 말뭉치가 존재하지 않기 때문에 표준 기계 번역 방법은 이 작업에 적합하지 않습니다. 대신 여기에는 대규모 언어 모델의 퓨샷 학습 기능이 사용됩니다. 특히, 비공식 증명과 해당 공식 스케치를 포함하는 몇 가지 예제 쌍을 사용하여 모델을 유도한 다음 변환할 비공식 증명을 사용한 다음 모델이 필요한 공식 스케치를 얻기 위해 후속 토큰을 생성하도록 합니다. 이 모델을 "자동 형식화기"라고 합니다.

그림 2. 증명 스케치의 개방형 추측 여기서 "자동 증명자"는 공식적으로 검증 가능한 증명을 생성할 수 있는 시스템을 의미합니다. 프레임워크는 자동 증명의 특정 선택에 불가지론적입니다. 이는 상징적 증명(예: 휴리스틱 증명 자동화 도구), 신경망 기반 증명 또는 하이브리드 접근 방식일 수 있습니다. 자동 증명자가 증명 스케치의 모든 공백을 성공적으로 채우면 문제의 사양과 비교하여 확인할 수 있는 최종 형식 증명을 반환합니다. 자동 증명이 실패하는 경우(예: 할당된 시간 제한을 초과하는 경우) 평가는 실패한 것으로 간주됩니다.
실험
연구원들은 miniF2F 데이터 세트에서 생성된 문제에 대한 형식적 증명을 포함하여 일련의 실험을 수행했으며 이 방법을 사용하여 많은 부분의 정리가 자동으로 증명될 수 있음을 보여주었습니다. 여기에서는 인간이 비공식 증명을 작성하거나 수학 텍스트에 대해 훈련된 대규모 언어 모델로 초안을 작성하는 두 가지 환경을 연구합니다. 이 두 가지 설정은 기존 이론을 형식화할 때 자주 발생하는 상황, 즉 비공식적인 증명이 있는 경우가 많지만 독자의 연습용으로 남겨두거나 여백의 제약으로 인해 누락되는 경우가 종종 있는 상황에 해당합니다.
표 1은 miniF2F 데이터 세트에서 발견된 성공적인 형식 증명의 비율을 보여줍니다. 결과에는 실험의 4가지 기준선과 사람이 작성한 증명 및 모델 생성 증명을 사용한 DSP 방법이 포함됩니다.
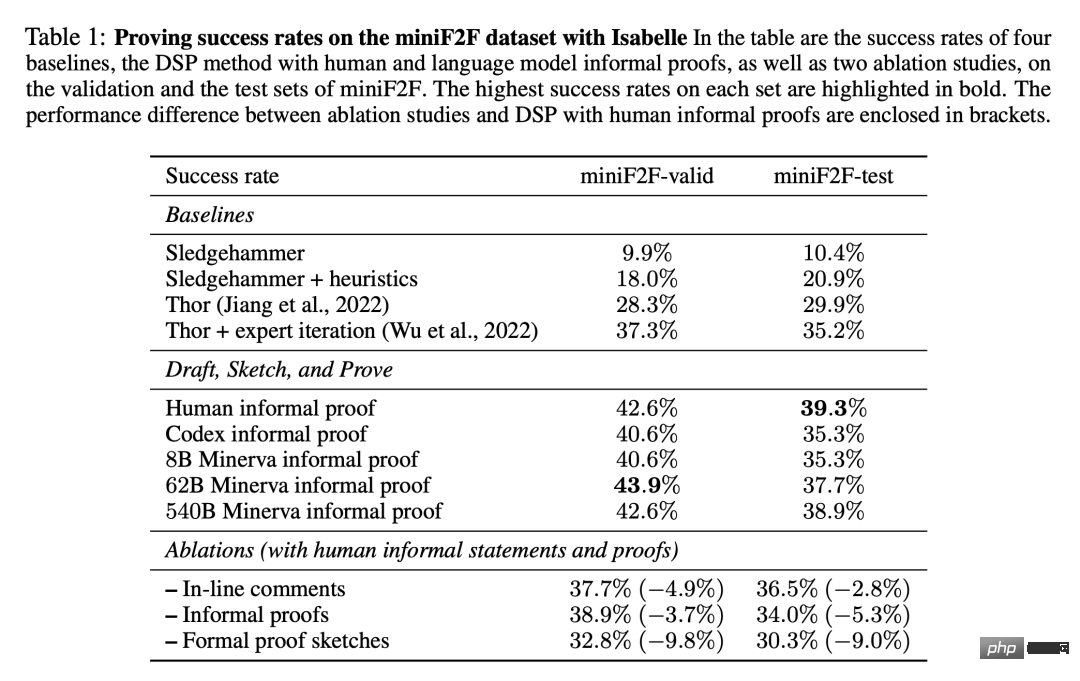
11개의 휴리스틱 전략이 첨부된 자동 증명은 Sledgehammer의 성능을 크게 향상시켜 miniF2F의 검증 세트에서 성공률을 9.9%에서 18.0%로 증가시키는 것을 볼 수 있습니다. , 10.4%에서 20.9%로 증가했다. 언어 모델과 증명 검색을 사용한 두 가지 기준선은 miniF2F 테스트 세트에서 각각 29.9%와 35.2%의 성공률을 달성했습니다.
인간이 작성한 비공식 증명을 기반으로 DSP 방식은 miniF2F의 검증 및 테스트 세트에서 42.6%와 39.3%의 성공률을 달성합니다. 488개 문제 중 총 200개 문제가 이런 방식으로 증명될 수 있습니다. Codex 모델과 Minerva(8B) 모델은 miniF2F의 문제를 해결할 때 매우 유사한 결과를 제공했습니다. 둘 다 자동 검증기가 검증 세트와 테스트 세트의 문제 중 각각 40.6%와 35.3%를 해결하도록 안내했습니다.
미네르바(62B) 모델로 전환했을 때 성공률은 각각 43.9%, 37.7%로 높아졌습니다. 사람이 작성한 비공식 증명에 비해 성공률은 검증 세트에서는 1.3% 더 높고 테스트 세트에서는 1.6% 더 낮습니다. 전체적으로 Minerva(62B) 모델은 miniF2F에서 사람이 작성한 증명보다 1개 적은 199개의 문제를 해결할 수 있습니다. Minerva(540B) 모델은 miniF2F 검증 세트와 테스트 세트의 문제를 각각 42.6%, 38.9% 해결했으며, 199개의 성공적인 증명도 생성했습니다.
DSP 방법은 인간을 사용한 비공식 증명 또는 언어 모델에 의해 생성된 비공식 증명 두 경우 모두에서 자동 증명을 효과적으로 안내합니다. DSP는 증명자의 성공률을 거의 두 배로 높이고 Isabelle을 사용하여 miniF2F에서 SOTA 성능을 생성합니다. 또한 더 큰 Minerva 모델은 자동화된 형식 증명자를 안내하는 데 있어서 인간만큼 도움이 됩니다.
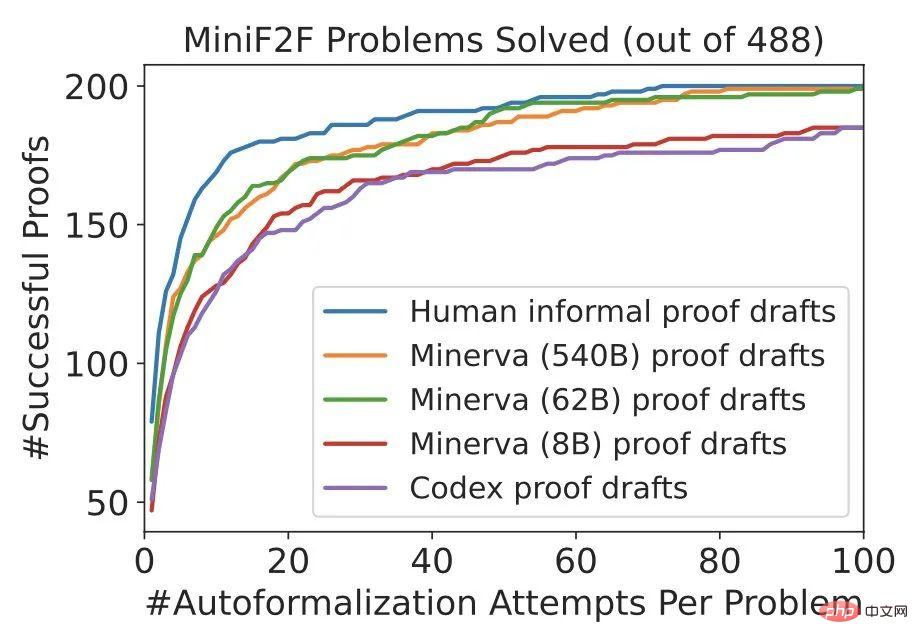
아래 그림과 같이 DSP 방식은 Sledgehammer + 휴리스틱 증명자의 성능을 크게 향상시켜(~20% -> ~40%) miniF2F에서 새로운 SOTA를 달성합니다.
Minerva의 62B 및 540B 버전은 인간 증명과 매우 유사한 증명을 생성합니다.
자세한 내용은 원문을 참고해주세요.
위 내용은 AI는 다시 한 번 수학 세계에 참여하고 새로운 DSP 방법은 기계 증명의 성공률을 두 배로 늘립니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7724
7724
 15
15
 1643
1643
 14
14
 1396
1396
 52
52
 1290
1290
 25
25
 1233
1233
 29
29
 Worldcoin (WLD) 가격 예측 2025-2031 : WLD가 2031 년까지 4 달러에 도달 할 것인가?
Apr 21, 2025 pm 02:42 PM
Worldcoin (WLD) 가격 예측 2025-2031 : WLD가 2031 년까지 4 달러에 도달 할 것인가?
Apr 21, 2025 pm 02:42 PM
Worldcoin (WLD)은 Cryptocurrency 시장에서 고유 한 생체 인정 및 개인 정보 보호 메커니즘으로 눈에 띄고 많은 투자자의 관심을 끌고 있습니다. WLD는 혁신적인 기술, 특히 OpenAi 인공 지능 기술과 함께 Altcoins에서 뛰어난 성과를 거두었습니다. 그러나 향후 몇 년 안에 디지털 자산은 어떻게 행동 할 것인가? WLD의 미래 가격을 함께 예측합시다. 2025 WLD 가격 예측은 2025 년 WLD에서 상당한 성장을 달성 할 것으로 예상됩니다. 시장 분석에 따르면 평균 WLD 가격은 최대 $ 1.36로 $ 1.31에 도달 할 수 있습니다. 그러나 곰 시장에서 가격은 약 $ 0.55로 떨어질 수 있습니다. 이러한 성장 기대는 주로 WorldCoin2에 기인합니다.
 크로스 체인 거래는 무엇을 의미합니까? 크로스 체인 거래는 무엇입니까?
Apr 21, 2025 pm 11:39 PM
크로스 체인 거래는 무엇을 의미합니까? 크로스 체인 거래는 무엇입니까?
Apr 21, 2025 pm 11:39 PM
크로스 체인 거래를 지원하는 교환 : 1. Binance, 2. Uniswap, 3. Sushiswap, 4. Curve Finance, 5. Thorchain, 6. 1inch Exchange, 7. DLN 거래,이 플랫폼은 다양한 기술을 통해 다중 체인 자산 거래를 지원합니다.
 Aavenomics는 AAVE 프로토콜 토큰을 수정하고 쿼럼 수의 사람들에게 도달 한 토큰 재구매를 소개하는 권장 사항입니다.
Apr 21, 2025 pm 06:24 PM
Aavenomics는 AAVE 프로토콜 토큰을 수정하고 쿼럼 수의 사람들에게 도달 한 토큰 재구매를 소개하는 권장 사항입니다.
Apr 21, 2025 pm 06:24 PM
Aavenomics는 AAVE 프로토콜 토큰을 수정하고 Aavedao의 쿼럼을 구현 한 Token Repos를 소개하는 제안입니다. AAVE 프로젝트 체인 (ACI)의 설립자 인 Marc Zeller는 X에서 이것을 발표하여 계약의 새로운 시대를 표시한다고 지적했습니다. AAVE 체인 이니셔티브 (ACI)의 설립자 인 Marc Zeller는 AAVENOMICS 제안서에 AAVE 프로토콜 토큰 수정 및 토큰 리포지션 도입이 포함되어 있다고 X에서 AAVEDAO에 대한 쿼럼을 달성했다고 발표했습니다. Zeller에 따르면, 이것은 계약의 새로운 시대를 나타냅니다. Aavedao 회원국은 수요일에 주당 100 인 제안을지지하기 위해 압도적으로 투표했습니다.
 통화에서 레버리지 교환 순위 순위 서클 통화 서클에서 상위 10 개의 레버리지 거래소의 최신 권장 사항
Apr 21, 2025 pm 11:24 PM
통화에서 레버리지 교환 순위 순위 서클 통화 서클에서 상위 10 개의 레버리지 거래소의 최신 권장 사항
Apr 21, 2025 pm 11:24 PM
2025 년에 레버리지 거래, 보안 및 사용자 경험에서 뛰어난 성능을 보이는 플랫폼은 다음과 같습니다. 1. OKX, 고주파 거래자에게 적합하여 최대 100 배의 레버리지를 제공합니다. 2. Binance, 전 세계의 다중 통화 거래자에게 적합하며 125 배 높은 레버리지를 제공합니다. 3. Gate.io, 전문 파생 상품 플레이어에게 적합하며 100 배의 레버리지를 제공합니다. 4. 초보자 및 소셜 트레이더에게 적합한 Bitget, 최대 100 배의 레버리지를 제공합니다. 5. 크라켄은 꾸준한 투자자에게 적합하며 5 배의 레버리지를 제공합니다. 6. Bybit, Altcoin Explorers에 적합하며 20 배의 레버리지를 제공합니다. 7. 저비용 거래자에게 적합한 Kucoin, 10 배의 레버리지를 제공합니다. 8. 비트 피 넥스, 시니어 플레이에 적합합니다
 하이브리드 블록 체인 거래 플랫폼은 무엇입니까?
Apr 21, 2025 pm 11:36 PM
하이브리드 블록 체인 거래 플랫폼은 무엇입니까?
Apr 21, 2025 pm 11:36 PM
cryptocurrency 교환 선택에 대한 제안 : 1. 유동성 요구 사항의 경우 우선 순위는 순서 깊이와 강한 변동성 저항으로 인해 Binance, Gate.io 또는 Okx입니다. 2. 규정 준수 및 보안, 코인베이스, 크라켄 및 쌍둥이 자리는 엄격한 규제 승인을 받았습니다. 3. Kucoin의 소프트 스테이 킹 및 Bybit의 파생 설계 혁신적인 기능은 고급 사용자에게 적합합니다.
 통화 서클 시장의 실시간 데이터에 대한 상위 10 개 무료 플랫폼 권장 사항이 출시됩니다.
Apr 22, 2025 am 08:12 AM
통화 서클 시장의 실시간 데이터에 대한 상위 10 개 무료 플랫폼 권장 사항이 출시됩니다.
Apr 22, 2025 am 08:12 AM
초보자에게 적합한 cryptocurrency 데이터 플랫폼에는 CoinmarketCap 및 비소 트럼펫이 포함됩니다. 1. CoinmarketCap은 초보자 및 기본 분석 요구에 대한 글로벌 실시간 가격, 시장 가치 및 거래량 순위를 제공합니다. 2. 비소 인용문은 중국 사용자가 저 위험 잠재적 프로젝트를 신속하게 선별하는 데 적합한 중국 친화적 인 인터페이스를 제공합니다.
 Binance 전체 프로세스 전략에 대한 커널 에어 드롭 보상을받는 방법
Apr 21, 2025 pm 01:03 PM
Binance 전체 프로세스 전략에 대한 커널 에어 드롭 보상을받는 방법
Apr 21, 2025 pm 01:03 PM
암호 화폐의 번화 한 세계에서는 새로운 기회가 항상 나타납니다. 현재 Kerneldao (Kernel) 에어 드롭 활동은 많은 관심을 끌고 많은 투자자들의 관심을 끌고 있습니다. 그렇다면이 프로젝트의 기원은 무엇입니까? BNB 보유자는 어떤 이점을 얻을 수 있습니까? 걱정하지 마십시오. 다음은 당신을 위해 하나씩 공개 할 것입니다.
 Rexas Finance (RXS)는 2025 년 Solana (Sol), Cardano (ADA), XRP 및 Dogecoin (Doge)을 능가 할 수 있습니다.
Apr 21, 2025 pm 02:30 PM
Rexas Finance (RXS)는 2025 년 Solana (Sol), Cardano (ADA), XRP 및 Dogecoin (Doge)을 능가 할 수 있습니다.
Apr 21, 2025 pm 02:30 PM
휘발성 cryptocurrency 시장에서 투자자들은 대중적인 통화를 넘어서는 대안을 찾고 있습니다. Solana (Sol), Cardano (ADA), XRP 및 Dogecoin (DOGE)과 같은 잘 알려진 암호 화폐도 시장 감정, 규제 불확실성 및 확장 성과 같은 도전에 직면 해 있습니다. 그러나 새로운 신흥 프로젝트 인 Rexasfinance (RXS)가 떠오르고 있습니다. 유명 인사 효과 나 과대 광고에 의존하지는 않지만 RWA (Ralld Assets)와 블록 체인 기술을 결합하여 투자자에게 혁신적인 투자 방법을 제공하는 데 중점을 둡니다. 이 전략은 2025 년의 가장 성공적인 프로젝트 중 하나가되기를 희망합니다. Rexasfi




