기계 학습 모델에 대한 최상의 임계값 설정: 0.5가 이진 분류에 대한 최상의 임계값입니까?

이진 분류의 경우 분류기는 실제 값 점수를 출력한 다음 값의 임계값을 지정하여 이진 응답을 생성합니다. 예를 들어, 로지스틱 회귀는 확률(0.0에서 1.0 사이의 값)을 출력합니다. 점수가 0.5 이상인 관측치는 양수 출력을 생성합니다(다른 많은 모델에서는 기본적으로 0.5 임계값을 사용함).

그러나 기본 0.5 임계값을 사용하는 것은 이상적이지 않습니다. 이 기사에서는 이진 분류기에서 최상의 임계값을 선택하는 방법을 보여 드리겠습니다. 이 기사에서는 Plumber를 사용하여 실험을 병렬로 실행하고 sklearn-evaluation을 사용하여 그래프를 생성합니다.

여기에서는 훈련 로지스틱 회귀를 예로 들어 보겠습니다. 모델이 유해한 콘텐츠(이미지, 비디오 등)가 포함된 게시물에 플래그를 지정한 다음 사람이 이를 보고 콘텐츠를 삭제해야 하는지 여부를 결정하는 콘텐츠 조정 시스템을 개발한다고 가정해 보겠습니다.

간단한 이진 분류기 구축

다음 코드 조각은 분류기를 교육합니다.

import matplotlib.pyplot as plt
 import matplotlib as mpl
 from sklearn import datasets
 from sklearn.linear_model import LogisticRegression
 from sklearn.model_selection import train_test_split
 from sklearn_evaluation.plot import ConfusionMatrix
 
 # matplotlib settings
 mpl.rcParams['figure.figsize'] = (4, 4)
 mpl.rcParams['figure.dpi'] = 150
 
 # create sample dataset
 X, y = datasets.make_classification(1000, 10, n_informative=5, class_sep=0.4)
 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
 
 # fit model
 clf = LogisticRegression()
 _ = clf.fit(X_train, y_train)

이제 테스트 세트에 대해 예측하고 혼동 행렬을 통해 성능을 평가해 보겠습니다.

# predict on the test set
 y_pred = clf.predict(X_test)
 
 # plot confusion matrix
 cm_dot_five = ConfusionMatrix(y_test, y_pred)
 cm_dot_five

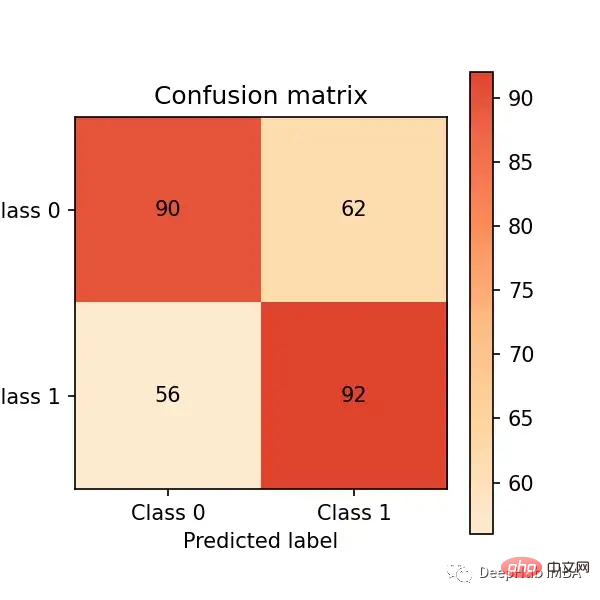
혼란 행렬은 모델 성능을 다음과 같이 요약합니다. 네 지역:

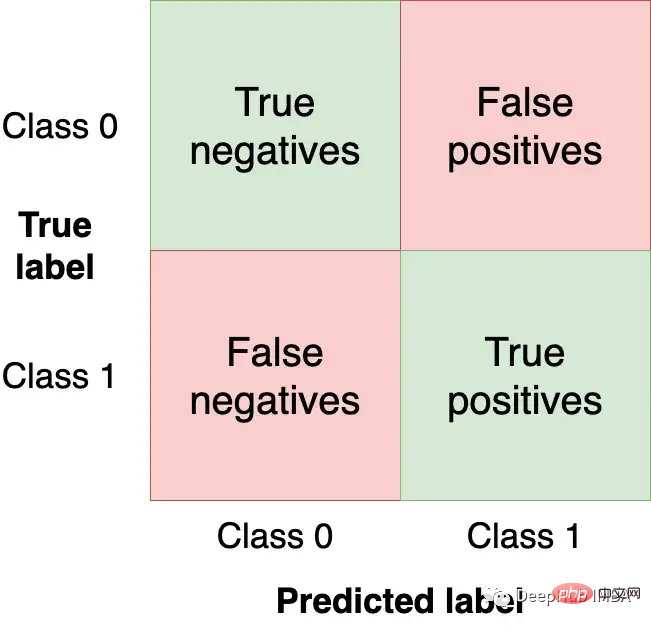
우리는 왼쪽 위와 오른쪽 아래 사분면에서 가능한 한 많은 관측값(테스트 세트에서)을 얻고 싶습니다. 이는 모델이 얻을 수 있는 올바른 관측값이기 때문입니다. 다른 사분면은 모델 오류입니다.

모델의 임계값을 변경하면 혼동 행렬의 값이 변경됩니다. 이전 예에서는 clf.predict를 사용하여 이진 응답이 반환되지만(즉, 임계값으로 0.5 사용) clf.predict_proba 함수를 사용하여 원시 확률을 얻고 사용자 정의 임계값을 사용할 수 있습니다.

y_score = clf.predict_proba(X_test)

다음을 수행할 수 있습니다. 더 큰 A 낮은 임계값(예: 더 많은 게시물을 유해한 게시물로 표시)을 설정하면 분류기가 더욱 공격적으로 변하고 새로운 혼동 행렬이 생성됩니다.

cm_dot_four = ConfusionMatrix(y_score[:, 1] >= 0.4, y_pred)

sklearn-evaluation 라이브러리를 사용하면 두 행렬을 쉽게 비교할 수 있습니다.

cm_dot_five + cm_dot_four

상단 삼각형의 임계값은 0.5이고 아래쪽은 임계값 0.4입니다.

• 두 모델 모두 동일한 수의 관측값에 대해 0을 예측합니다(우연의 일치입니다). 0.5 임계값: (90 + 56 = 146). 0.4 임계값: (78 + 68 = 146)
• 임계값을 낮추면 더 많은 거짓음성이 발생합니다(56에서 68로)
• 임계값을 낮추면 참양성이 크게 늘어납니다(92에서 154로)

작은 임계값 변경 혼동 행렬에 큰 영향을 미칩니다. 우리는 두 가지 임계값만 분석했습니다. 그런 다음 모든 값에 걸쳐 모델 성능을 분석할 수 있으면 임계값 역학을 더 잘 이해할 수 있습니다. 하지만 그렇게 되기 전에 모델 평가를 위한 새로운 측정항목을 정의해야 합니다.

지금까지 우리는 절대 숫자를 사용하여 모델을 평가했습니다. 비교와 평가를 용이하게 하기 위해 이제 두 개의 정규화된 측정항목을 정의하겠습니다(해당 값은 0.0에서 1.0 사이입니다).

정밀도는 라벨이 지정된 관찰된 이벤트의 비율입니다(예: 모델이 유해하다고 간주하는 게시물, 유해한 게시물). 리콜은 우리 모델에 의해 검색된 실제 이벤트의 비율입니다(즉, 모든 유해 게시물 중에서 우리가 탐지할 수 있었던 비율).

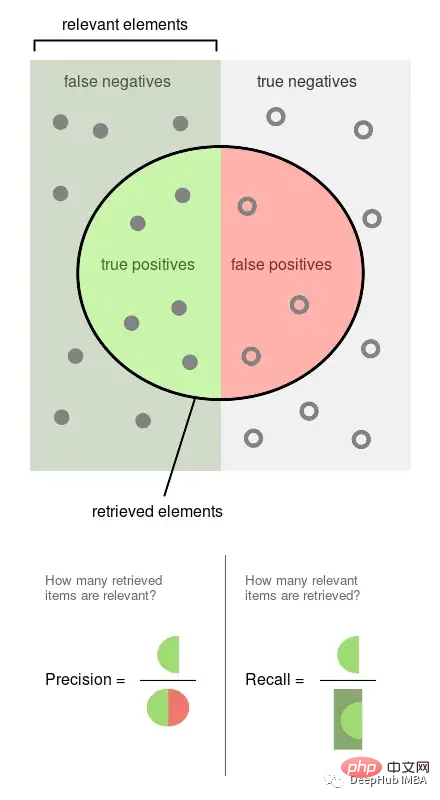
위 그림은 Wikipedia에서 가져온 것으로, 이 두 지표가 어떻게 계산되는지 잘 보여줍니다. 정밀도와 재현율은 모두 비례하므로 둘 다 0:1 비율입니다.

실험을 실행하세요

임계값이 임계값에 미치는 영향을 더 잘 이해하기 위해 여러 임계값을 기반으로 정밀도, 재현율 및 기타 통계를 얻을 것입니다. 또한 변동성을 측정하기 위해 이 실험을 여러 번 반복할 것입니다.

이 섹션의 명령은 모두 bash 명령입니다. Jupyter를 사용하는 경우 %%sh 매직 명령을 사용할 수 있습니다.

여기에서는 Plumber Cloud를 사용하여 실험을 실행합니다. 실험을 병렬로 실행하고 결과를 빠르게 검색할 수 있기 때문입니다.

모델에 맞는 노트북을 만들고 여러 임계값에 대한 통계를 계산하여 동일한 노트북을 20번 병렬로 실행했습니다.

curl -O https://raw.githubusercontent.com/ploomber/posts/master/threshold/fit.ipynb?utm_source=medium&utm_medium=blog&utm_campaign=threshold

이 노트북을 실행해 보겠습니다(파일의 구성에 따라 Plumber Cloud가 20번 병렬로 실행하도록 지정됩니다).

ploomber cloud nb fit.ipynb

몇 분 안에 20개의 실험이 완료되는 것을 확인할 수 있습니다.

ploomber cloud status @latest --summary
 
 status count
 -------- -------
 finished 20
 
 Pipeline finished. Check outputs:
 $ ploomber cloud products

실험 결과를 .csv 파일로 저장:

ploomber cloud download 'threshold-selection/*.csv' --summary

실험 결과 시각화

는 모든 실험 결과를 로드하고 한 번에 플롯합니다.

 from glob import glob
 
 import pandas as pd
 import numpy as np
 paths = glob('threshold-selection/**/*.csv')
 metrics = [pd.read_csv(path) for path in paths]
 
 for idx, df in enumerate(metrics):
plt.plot(df.threshold, df.precision, color='blue', alpha=0.2,
label='precision' if idx == 0 else None)
plt.plot(df.threshold, df.recall, color='green', alpha=0.2,
label='recall' if idx == 0 else None)
plt.plot(df.threshold, df.f1, color='orange', alpha=0.2,
label='f1' if idx == 0 else None)
 
 
 plt.grid()
 plt.legend()
 plt.xlabel('Threshold')
 plt.ylabel('Metric value')
 
 for handle in plt.legend().legendHandles:
handle.set_alpha(1)
 
 ax = plt.twinx()
 
 for idx, df in enumerate(metrics):
ax.plot(df.threshold, df.n_flagged,
label='flagged' if idx == 0 else None,
color='red', alpha=0.2)
 
 plt.ylabel('Flagged')
 ax.legend(loc=0)
 ax.legend().legendHandles[0].set_alpha(1)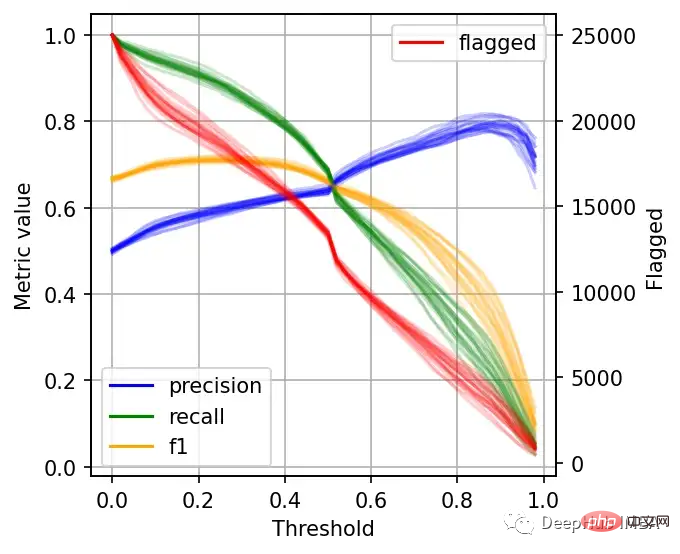

左边的刻度(从0到1)是我们的三个指标:精度、召回率和F1。F1分为精度与查全率的调和平均值，F1分的最佳值为1.0，最差值为0.0;F1对精度和召回率都是相同对待的，所以你可以看到它在两者之间保持平衡。如果你正在处理一个精确度和召回率都很重要的用例，那么最大化F1是一种可以帮助你优化分类器阈值的方法。

这里还包括一条红色曲线(右侧的比例)，显示我们的模型标记为有害内容的案例数量。

在这个的内容审核示例中，可能有X个的工作人员来人工审核模型标记的有害帖子，但是他们人数是有限的，因此考虑标记帖子的总数可以帮助我们更好地选择阈值:例如每天只能检查5000个帖子，那么模型找到10,000帖并不会带来任何的提高。如果我人工每天可以处理10000贴，但是模型只标记了100贴，那么显然也是浪费的。

当设置较低的阈值时，有较高的召回率(我们检索了大部分实际上有害的帖子)，但精度较低(包含了许多无害的帖子)。如果我们提高阈值，情况就会反转:召回率下降(错过了许多有害的帖子)，但精确度很高(大多数标记的帖子都是有害的)。

所以在为我们的二元分类器选择阈值时，我们必须在精度或召回率上妥协，因为没有一个分类器是完美的。我们来讨论一下如何推理选择合适的阈值。

选择最佳阈值

右边的数据会产生噪声(较大的阈值)。需要稍微清理一下，我们将重新创建这个图，我们将绘制2.5%、50%和97.5%的百分位数，而不是绘制所有值。

shape = (df.shape[0], len(metrics))
 precision = np.zeros(shape)
 recall = np.zeros(shape)
 f1 = np.zeros(shape)
 n_flagged = np.zeros(shape)
 for i, df in enumerate(metrics):
precision[:, i] = df.precision.values
recall[:, i] = df.recall.values
f1[:, i] = df.f1.values
n_flagged[:, i] = df.n_flagged.values
 precision_ = np.quantile(precision, q=0.5, axis=1)
 recall_ = np.quantile(recall, q=0.5, axis=1)
 f1_ = np.quantile(f1, q=0.5, axis=1)
 n_flagged_ = np.quantile(n_flagged, q=0.5, axis=1)
 plt.plot(df.threshold, precision_, color='blue', label='precision')
 plt.plot(df.threshold, recall_, color='green', label='recall')
 plt.plot(df.threshold, f1_, color='orange', label='f1')
 
 plt.fill_between(df.threshold, precision_interval[0],
precision_interval[1], color='blue',
alpha=0.2)
 
 plt.fill_between(df.threshold, recall_interval[0],
recall_interval[1], color='green',
alpha=0.2)
 
 
 plt.fill_between(df.threshold, f1_interval[0],
f1_interval[1], color='orange',
alpha=0.2)
 plt.xlabel('Threshold')
 plt.ylabel('Metric value')
 plt.legend()
 
 ax = plt.twinx()
 ax.plot(df.threshold, n_flagged_, color='red', label='flagged')
 ax.fill_between(df.threshold, n_flagged_interval[0],
n_flagged_interval[1], color='red',
alpha=0.2)
 
 ax.legend(loc=3)
 
 plt.ylabel('Flagged')
 plt.grid()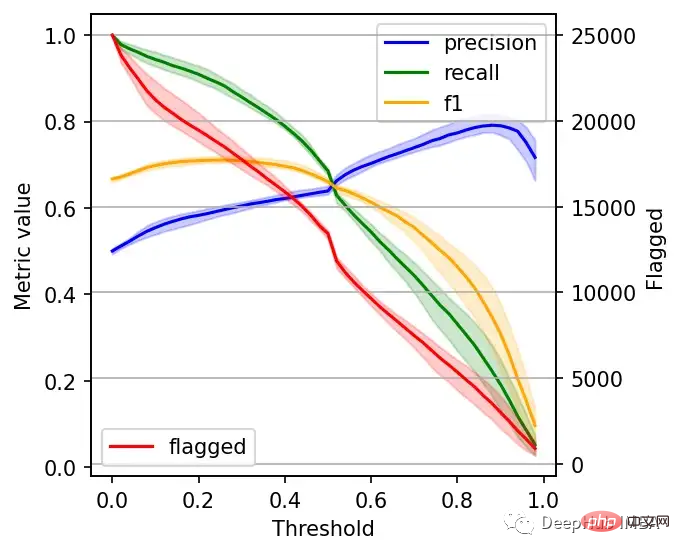

我们可以根据自己的需求选择阈值，例如检索尽可能多的有害帖子(高召回率)是否更重要?还是要有更高的确定性，我们标记的必须是有害的(高精度)?

如果两者都同等重要，那么在这些条件下优化的常用方法就是最大化F-1分数:

idx = np.argmax(f1_)
 prec_lower, prec_upper = precision_interval[0][idx], precision_interval[1][idx]
 rec_lower, rec_upper = recall_interval[0][idx], recall_interval[1][idx]
 threshold = df.threshold[idx]
 
 print(f'Max F1 score: {f1_[idx]:.2f}')
 print('Metrics when maximizing F1 score:')
 print(f' - Threshold: {threshold:.2f}')
 print(f' - Precision range: ({prec_lower:.2f}, {prec_upper:.2f})')
 print(f' - Recall range: ({rec_lower:.2f}, {rec_upper:.2f})')
 
 #结果
 Max F1 score: 0.71
 Metrics when maximizing F1 score:
- Threshold: 0.26
- Precision range: (0.58, 0.61)
- Recall range: (0.86, 0.90)

在很多情况下很难决定这个折中，所以加入一些约束条件会有一些帮助。

假设我们有10个人审查有害的帖子，他们可以一起检查5000个。那么让我们看看指标，如果我们修改了阈值，让它标记了大约5000个帖子:

idx = np.argmax(n_flagged_ <= 5000)
 
 prec_lower, prec_upper = precision_interval[0][idx], precision_interval[1][idx]
 rec_lower, rec_upper = recall_interval[0][idx], recall_interval[1][idx]
 threshold = df.threshold[idx]
 
 print('Metrics when limiting to a maximum of 5,000 flagged events:')
 print(f' - Threshold: {threshold:.2f}')
 print(f' - Precision range: ({prec_lower:.2f}, {prec_upper:.2f})')
 print(f' - Recall range: ({rec_lower:.2f}, {rec_upper:.2f})')
 
 # 结果
 Metrics when limiting to a maximum of 5,000 flagged events:
- Threshold: 0.82
- Precision range: (0.77, 0.81)
- Recall range: (0.25, 0.36)

如果需要进行汇报，我们可以在在展示结果时展示一些替代方案:比如在当前约束条件下(5000个帖子)的模型性能，以及如果我们增加团队(比如通过增加一倍的规模)，我们可以做得更好。

总结

二元分类器的最佳阈值是针对业务结果进行优化并考虑到流程限制的阈值。通过本文中描述的过程，你可以更好地为用例决定最佳阈值。

另外，Ploomber Cloud!提供一些免费的算力!如果你需要一些免费的服务可以试试它。

위 내용은 기계 학습 모델에 대한 최상의 임계값 설정: 0.5가 이진 분류에 대한 최상의 임계값입니까?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!