계산 복잡성은 실행 시 특정 알고리즘이 소비하는 계산 리소스(시간 및 공간)를 측정한 것입니다.
계산 복잡도는 두 가지 범주로 나뉩니다.
1. 시간 복잡도
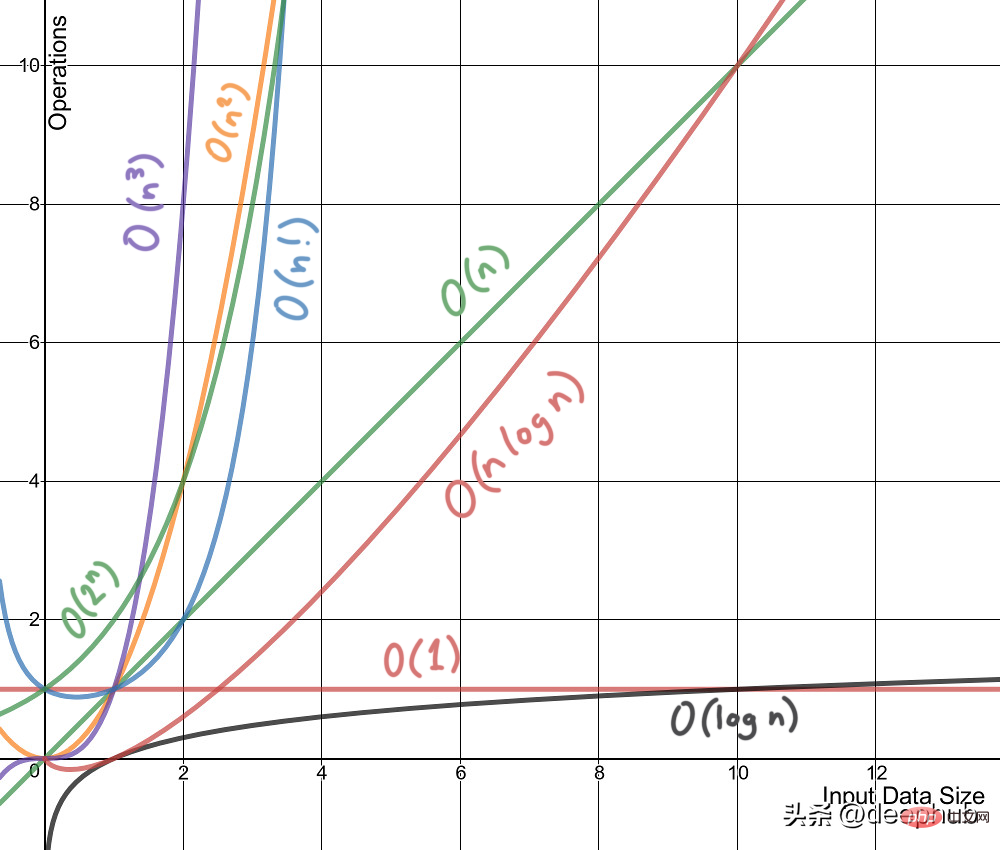
시간 복잡도는 특정 기계나 조건에서 알고리즘이나 코드가 실행되는 데 걸리는 시간을 측정한 것이 아닙니다. 시간 복잡도는 일반적으로 시간 복잡도를 의미하며, 이는 알고리즘의 실행 시간을 정성적으로 설명하고 다른 알고리즘을 실행하지 않고도 비교할 수 있게 해주는 함수입니다. 예를 들어, O(n)을 사용하는 알고리즘은 성장률이 O(n²)보다 낮기 때문에 항상 O(n²)보다 더 나은 성능을 발휘합니다.
2. 공간 복잡도
시간 복잡도가 함수인 것처럼 공간 복잡도도 마찬가지입니다. 개념적으로는 시간복잡도와 동일합니다. 시간을 공간으로 바꾸면 됩니다. Wikipedia는 공간 복잡성을 다음과 같이 정의합니다.
알고리즘이나 컴퓨터 프로그램의 공간 복잡성은 입력된 기능 수의 함수로서 계산 문제의 인스턴스를 해결하는 데 필요한 저장 공간의 양입니다.
아래에서는 몇 가지 일반적인 기계 학습 알고리즘의 계산 복잡성을 정리했습니다.
1. 선형 회귀
- n= 훈련 샘플 수, f = 특성 수
- 훈련 시간 복잡도: O(f²n+f³)
- 예측 시간 복잡도: O(f)
- 런타임 공간 복잡도: O (f)
2. 로지스틱 회귀:
- n= 훈련 샘플 수, f = 특징 수
- 훈련 시간 복잡도: O(f*n)
- 예측 시간 복잡도: O(f)
- 실행 시간 공간 복잡도: O(f)
3. 지원 벡터 머신:
- n= 훈련 샘플 수, f = 특징 수, s= 지원 벡터 수
- 교육 시간 복잡도: O(n²) O(n³)까지 훈련 시간 복잡도는 커널에 따라 다릅니다.
- 예측 시간 복잡도: O(f) ~ O(s*f): 선형 커널은 O(f), RBF 및 다항식은 O(s*f)
- 런타임 공간 복잡도: O(s)
4 . 나이브 베이즈:
- n= 훈련 샘플 수, f = 특징 수, c = 분류를 위한 범주 수
- 훈련 시간 복잡도: O(n*f*c)
- 예측 시간 복잡도: O(c *f)
- 런타임 공간 복잡성: O(c*f)
5. 결정 트리:
- n= 훈련 샘플 수, f = 기능 수, d = 트리 깊이, p = 노드 수
- 훈련 시간 복잡도: O(n*log(n)*f)
- 예측 시간 복잡도: O(d)
- 런타임 공간 복잡도: O(p)
6. Random Forest:
- n= 훈련 샘플 수, f = 특징 수, k = 트리 수, p = 트리의 노드 수, d = 트리 깊이
- 훈련 시간 복잡도: O(n*log(n) *f*k )
- 예측 시간 복잡도: O(d*k)
- 런타임 공간 복잡도: O(p*k)
7.K 가장 가까운 이웃:
n= 훈련 샘플 수, f = 특징 수, k = 가장 가까운 이웃의 수
Brute:
- 훈련 시간 복잡도: O(1)
- 예측 시간 복잡도: O(n*f+k*f)
- 런타임 공간 복잡도: O(n*f)
kd-tree:
- 훈련 시간 복잡도: O(f*n*log(n))
- 예측 시간 복잡도: O(k*log(n))
- 런타임 공간 복잡도: O(n*f)
8, K-군집화 의미:
- n= 훈련 샘플 수, f = 특징 수, k= 군집 수, i = 반복 수
- 훈련 시간 복잡도:O(n*f*k *i)
- 런타임 공간 복잡도: O(n*f+k*f)
위 내용은 8가지 일반적인 기계 학습 알고리즘의 계산 복잡성 요약의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
