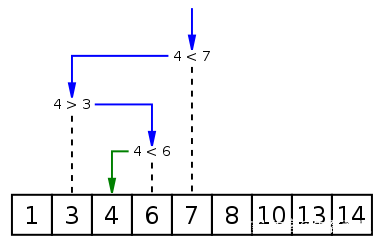
이진 검색은 정렬된 배열에서 특정 요소를 찾는 검색 알고리즘입니다. 검색 과정은 배열의 중간 요소부터 시작되며, 중간 요소가 발견될 요소인 경우 특정 요소가 중간 요소보다 크거나 작을 경우 검색 과정이 종료됩니다. 중간 요소보다 크거나 작은 배열의 시작과 마찬가지로 중간 요소부터 비교를 시작합니다. 특정 단계에서 배열이 비어 있으면 찾을 수 없다는 의미입니다. 이 검색 알고리즘은 비교할 때마다 검색 범위를 절반으로 줄입니다.
# 返回 x 在 arr 中的索引，如果不存在返回 -1
def binarySearch (arr, l, r, x):
# 基本判断
if r >= l:
mid = int(l + (r - l)/2)
# 元素整好的中间位置
if arr[mid] == x:
return mid
# 元素小于中间位置的元素，只需要再比较左边的元素
elif arr[mid] > x:
return binarySearch(arr, l, mid-1, x)
# 元素大于中间位置的元素，只需要再比较右边的元素
else:
return binarySearch(arr, mid+1, r, x)
else:
# 不存在
return -1
# 测试数组
arr = [ 2, 3, 4, 10, 40]
x = int(input('请输入元素：'))
# 函数调用
result = binarySearch(arr, 0, len(arr)-1, x)
if result != -1:
print("元素在数组中的索引为 %d" % result)
else:
print("元素不在数组中")실행 결과:
요소를 입력하세요: 4
배열에 있는 요소의 인덱스는 2
요소를 입력하세요: 5
요소가 배열에 없습니다
선형 검색: 찾으려는 특정 값을 찾을 때까지 배열의 각 요소를 특정 순서로 확인하는 것을 말합니다.
def search(arr, n, x):
for i in range (0, n):
if (arr[i] == x):
return i
return -1
# 在数组 arr 中查找字符 D
arr = [ 'A', 'B', 'C', 'D', 'E' ]
x = input("请输入要查找的元素：")
n = len(arr)
result = search(arr, n, x)
if(result == -1):
print("元素不在数组中")
else:
print("元素在数组中的索引为", result)실행 결과:
찾고 있는 요소를 입력하세요: A
배열에 있는 요소의 인덱스는 0
찾고 있는 요소를 입력하세요: a
요소는 다음과 같습니다. not in the array
Insertion Sort: 간단하고 직관적인 정렬 알고리즘입니다. 정렬되지 않은 데이터의 경우 정렬된 시퀀스의 뒤에서 앞으로 스캔하여 해당 위치를 찾아 삽입합니다.
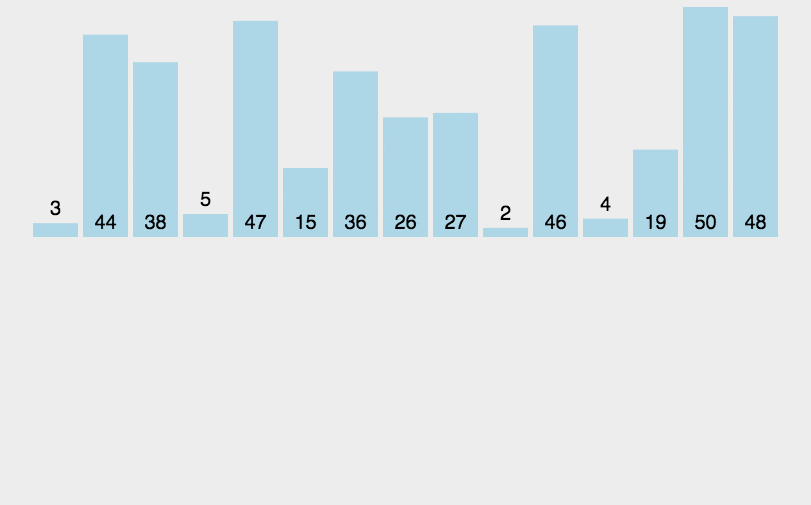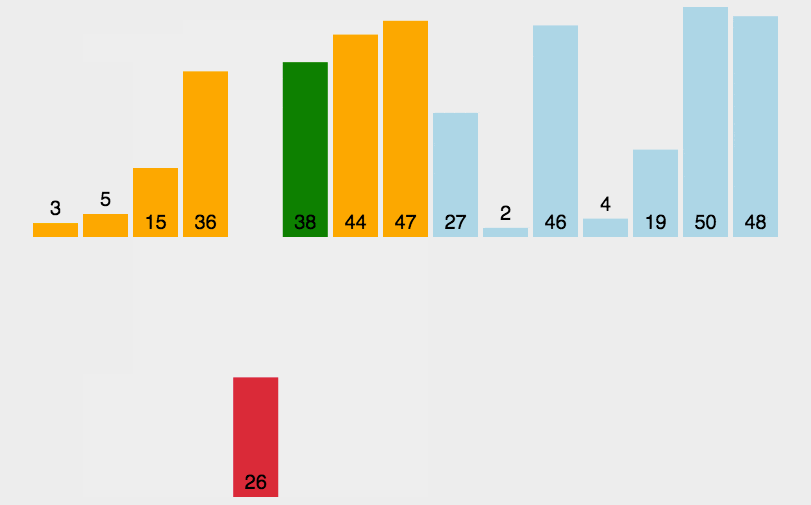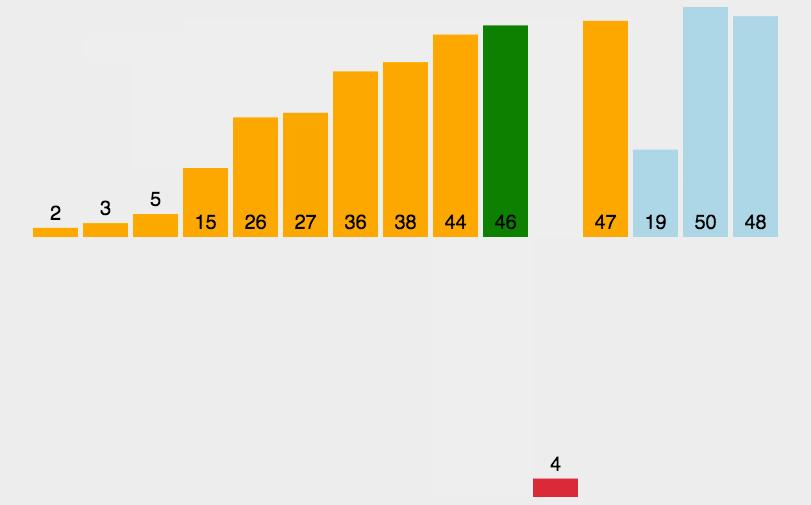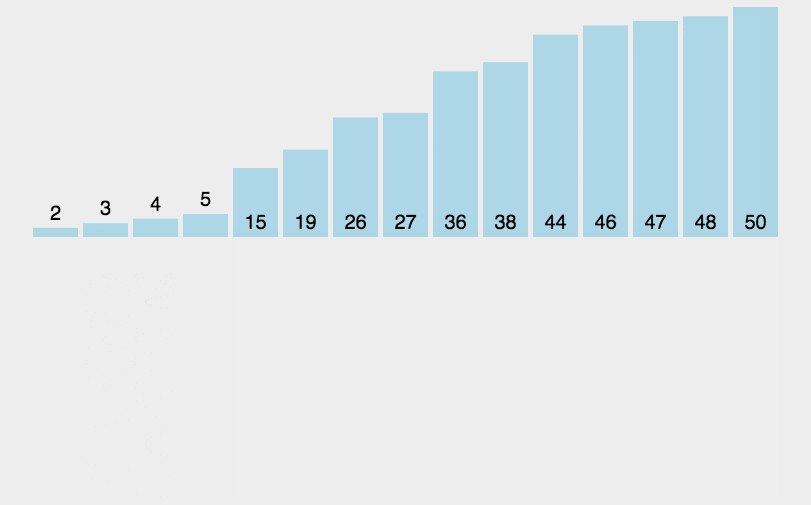
def insertionSort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i-1
while j >= 0 and key < arr[j]:
arr[j+1] = arr[j]
j -= 1
arr[j+1] = key
arr = [12, 11, 13, 5, 6, 7, 9, 9, 17]
insertionSort(arr)
print("排序后的数组:")
print(arr)실행 결과:
sorted array:
[5, 6, 7, 9, 9, 11, 12, 13, 17]
물론 이렇게도 쓸 수 있습니다.
list1 = [12, 11, 13, 5, 6, 7, 9, 9, 17]
for i in range(len(list1)-1, 0, -1):
for j in range(0, i):
if list1[i] < list1[j]:
list1[i], list1[j] = list1[j], list1[i]
print(list1)Quick sort; 분할 정복 전략을 사용하여 시퀀스(리스트)를 두 개의 하위 시퀀스, 작은 하위 시퀀스와 큰 하위 시퀀스로 나눈 다음 두 하위 시퀀스를 재귀적으로 정렬합니다.
단계는 다음과 같습니다.
피벗 값 선택: "피벗"(피벗)이라고 하는 요소를 시퀀스에서 선택합니다.
분할: 모든 항목이 값이 피벗 값보다 작습니다. 작은 요소는 피벗 앞에 배치되고 피벗 값보다 큰 요소는 모두 피벗 뒤에 배치됩니다(피벗 값과 같은 숫자는 양쪽으로 갈 수 있음). 이 나누기가 완료되면 참조 값 정렬이 완료됩니다.
하위 시퀀스 재귀적으로 정렬: 참조 값보다 작은 요소의 하위 시퀀스와 참조 값보다 큰 요소의 하위 시퀀스를 반복적으로 정렬합니다.
아래로 반복되는 판단 조건은 시퀀스의 크기가 0 또는 1이라는 것입니다. 이때 시퀀스는 분명히 순서대로입니다.
벤치마크 값을 선택하는 몇 가지 구체적인 방법이 있습니다. 이 선택 방법은 정렬 시간 성능에 결정적인 영향을 미칩니다.
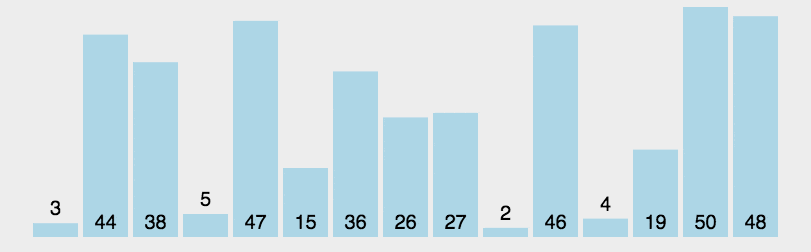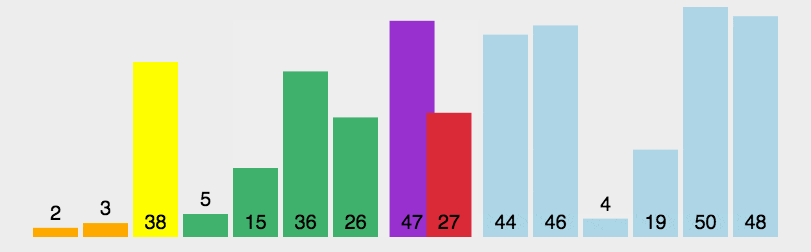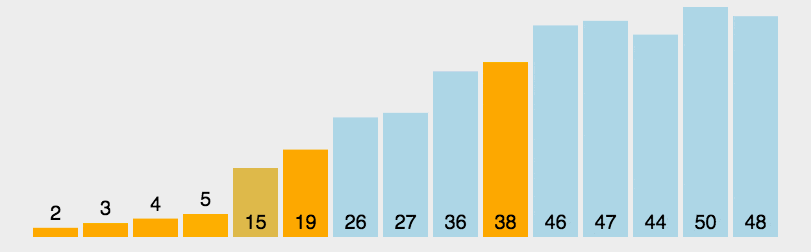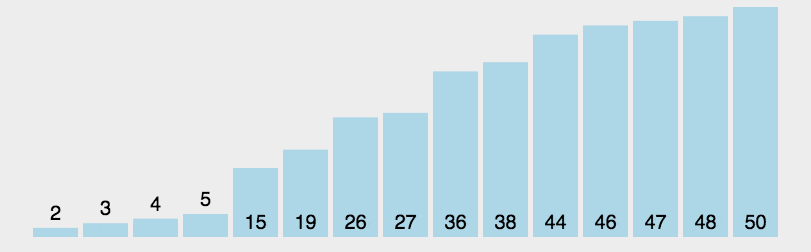
def partition(arr, low, high):
i = (low-1) # 最小元素索引
pivot = arr[high]
for j in range(low, high):
# 当前元素小于或等于 pivot
if arr[j] <= pivot:
i = i+1
arr[i], arr[j] = arr[j], arr[i]
arr[i+1], arr[high] = arr[high], arr[i+1]
return (i+1)
# arr[] --> 排序数组
# low --> 起始索引
# high --> 结束索引
# 快速排序函数
def quickSort(arr, low, high):
if low < high:
pi = partition(arr, low, high)
quickSort(arr, low, pi-1)
quickSort(arr, pi+1, high)
return arr
arr = [10, 7, 8, 9, 1, 5]
n = len(arr)
print("排序后的数组:")
print(quickSort(arr, 0, n-1))실행 결과:
sorted array:
[1, 5, 7, 8, 9, 10]
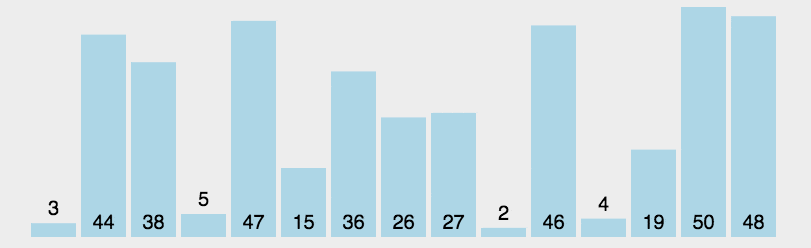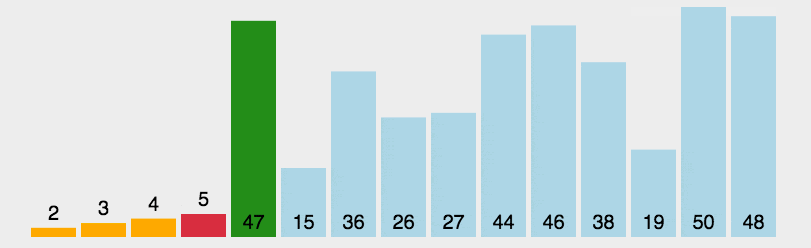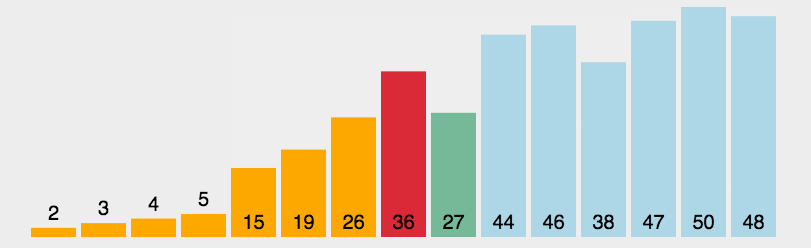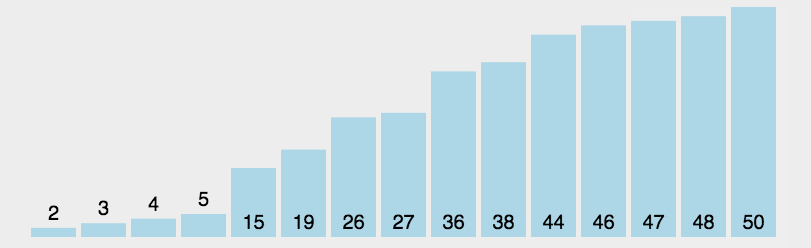
Selection sort: Yes 간단하고 직관적인 정렬 알고리즘 . 작동 방식은 다음과 같습니다.
먼저 정렬되지 않은 시퀀스에서 가장 작은(큰) 요소를 찾아 정렬된 시퀀스의 시작 부분에 저장한 다음, 정렬되지 않은 나머지 요소에서 계속해서 가장 작은(큰) 요소를 찾아 정렬된 시퀀스의 끝에 넣습니다. 순서. 모든 요소가 정렬될 때까지 계속됩니다.
A = [64, 25, 12, 22, 11]
for i in range(len(A)):
min_idx = i
for j in range(i+1, len(A)):
if A[min_idx] > A[j]:
min_idx = j
A[i], A[min_idx] = A[min_idx], A[i]
print("排序后的数组：")
print(A)실행 결과:
정렬된 배열:
[11, 12, 22, 25, 64]
def bubbleSort(arr):
n = len(arr)
# 遍历所有数组元素
for i in range(n):
# Last i elements are already in place
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
return arr
arr = [64, 34, 25, 12, 22, 11, 90]
print("排序后的数组:")
print(bubbleSort(arr))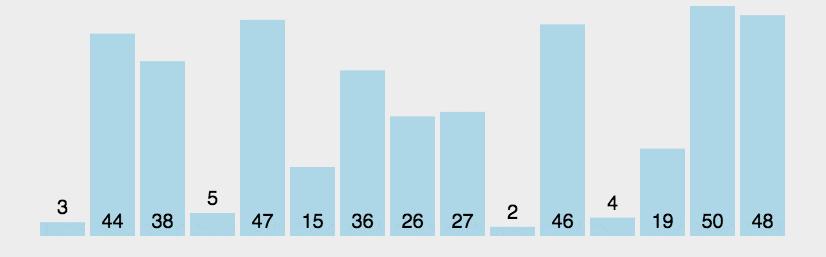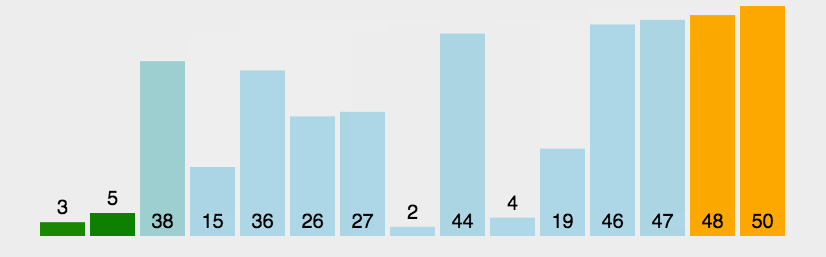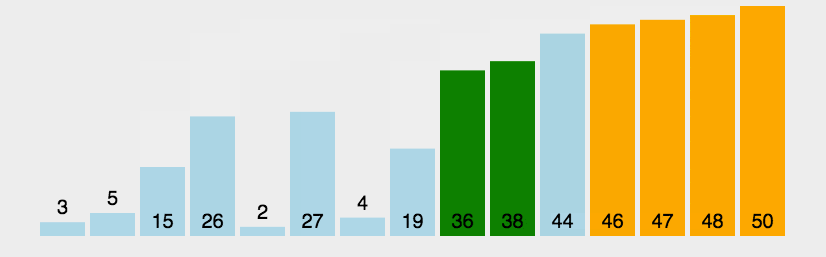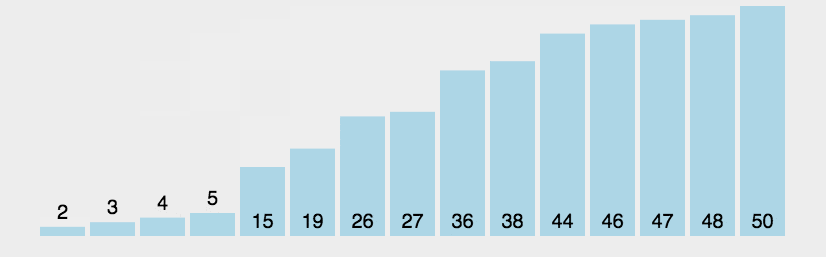
실행 결과:
정렬된 배열:
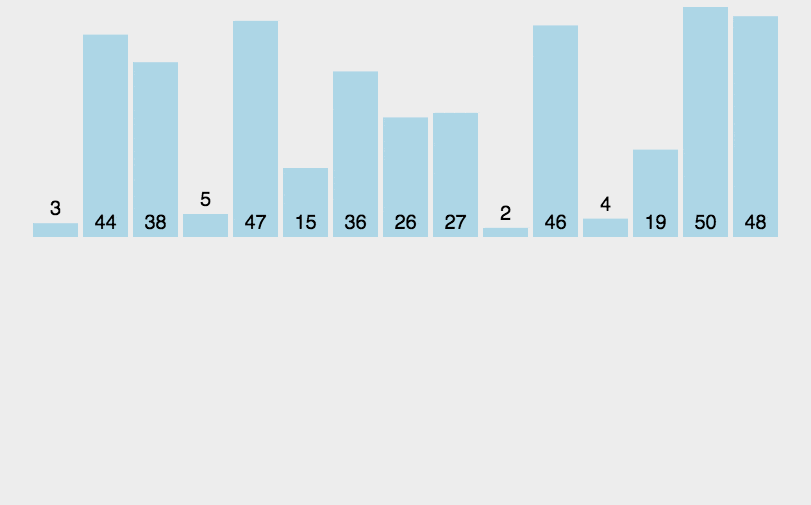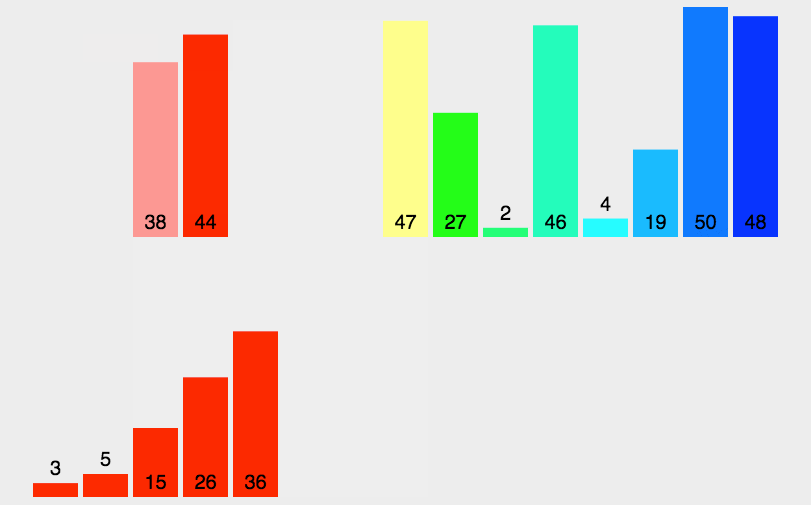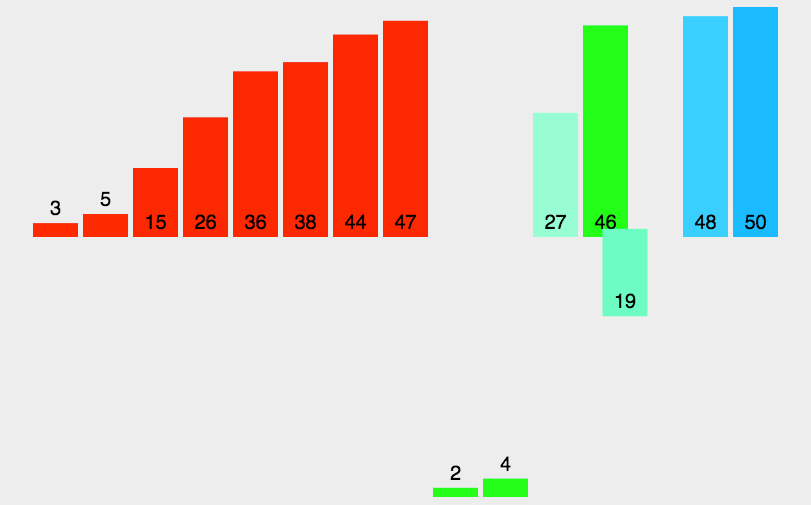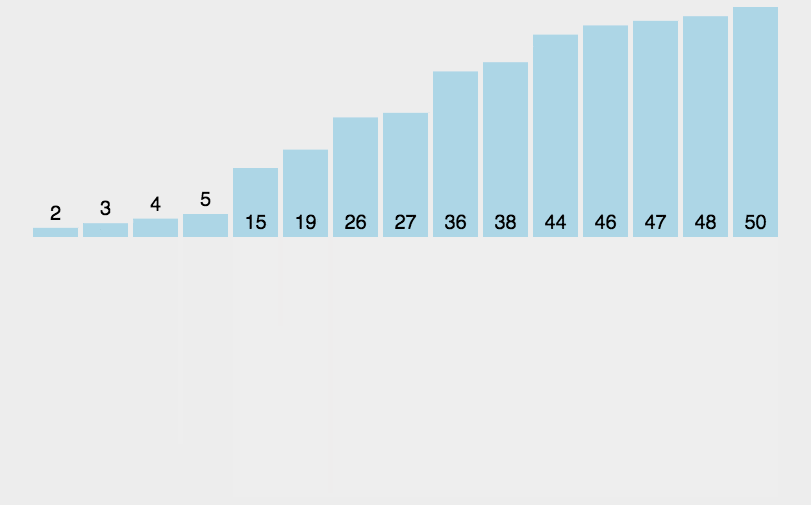
[11, 12, 22, 25, 34, 64, 90]归并排序（Merge sort，或mergesort）：，是创建在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。
分治法:
分割：递归地把当前序列平均分割成两半。
集成：在保持元素顺序的同时将上一步得到的子序列集成到一起（归并）。
def merge(arr, l, m, r):
n1 = m - l + 1
n2 = r - m
# 创建临时数组
L = [0] * (n1)
R = [0] * (n2)
# 拷贝数据到临时数组 arrays L[] 和 R[]
for i in range(0, n1):
L[i] = arr[l + i]
for j in range(0, n2):
R[j] = arr[m + 1 + j]
# 归并临时数组到 arr[l..r]
i = 0 # 初始化第一个子数组的索引
j = 0 # 初始化第二个子数组的索引
k = l # 初始归并子数组的索引
while i < n1 and j < n2:
if L[i] <= R[j]:
arr[k] = L[i]
i += 1
else:
arr[k] = R[j]
j += 1
k += 1
# 拷贝 L[] 的保留元素
while i < n1:
arr[k] = L[i]
i += 1
k += 1
# 拷贝 R[] 的保留元素
while j < n2:
arr[k] = R[j]
j += 1
k += 1
def mergeSort(arr, l, r):
if l < r:
m = int((l+(r-1))/2)
mergeSort(arr, l, m)
mergeSort(arr, m+1, r)
merge(arr, l, m, r)
return arr
print ("给定的数组")
arr = [12, 11, 13, 5, 6, 7, 13]
print(arr)
n = len(arr)
mergeSort(arr, 0, n-1)
print("排序后的数组")
print(arr)运行结果：
给定的数组
[12, 11, 13, 5, 6, 7, 13]
排序后的数组
[5, 6, 7, 11, 12, 13, 13]
堆排序（Heapsort）：是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。
def heapify(arr, n, i):
largest = i
l = 2 * i + 1 # left = 2*i + 1
r = 2 * i + 2 # right = 2*i + 2
if l < n and arr[i] < arr[l]:
largest = l
if r < n and arr[largest] < arr[r]:
largest = r
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i] # 交换
def heapSort(arr):
n = len(arr)
# Build a maxheap.
for i in range(n, -1, -1):
heapify(arr, n, i)
# 一个个交换元素
for i in range(n-1, 0, -1):
arr[i], arr[0] = arr[0], arr[i] # 交换
heapify(arr, i, 0)
return arr
arr = [12, 11, 13, 5, 6, 7, 13, 18]
heapSort(arr)
print("排序后的数组")
print(heapSort(arr))运行结果：
排序后的数组
[5, 6, 7, 12, 11, 13, 13, 18]
计数排序：的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。
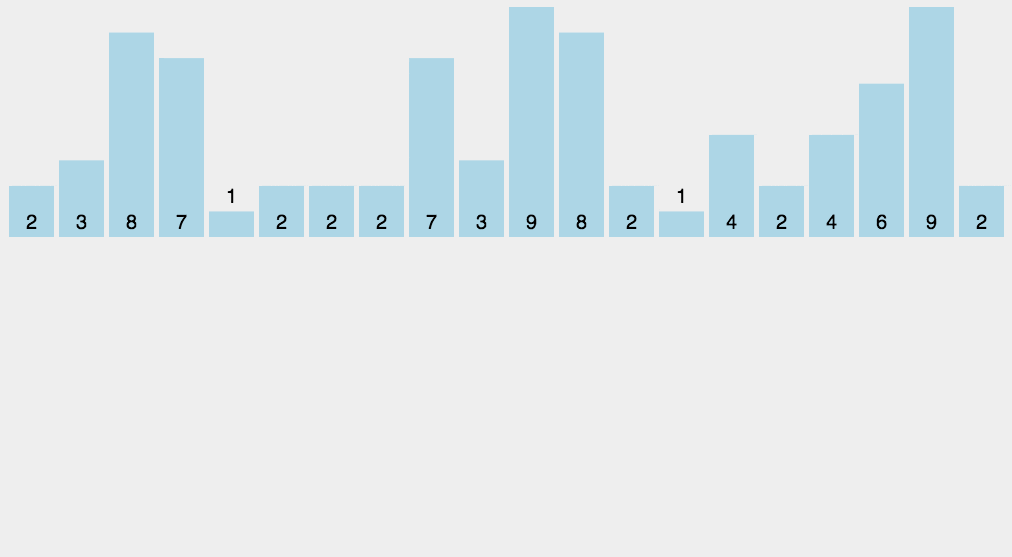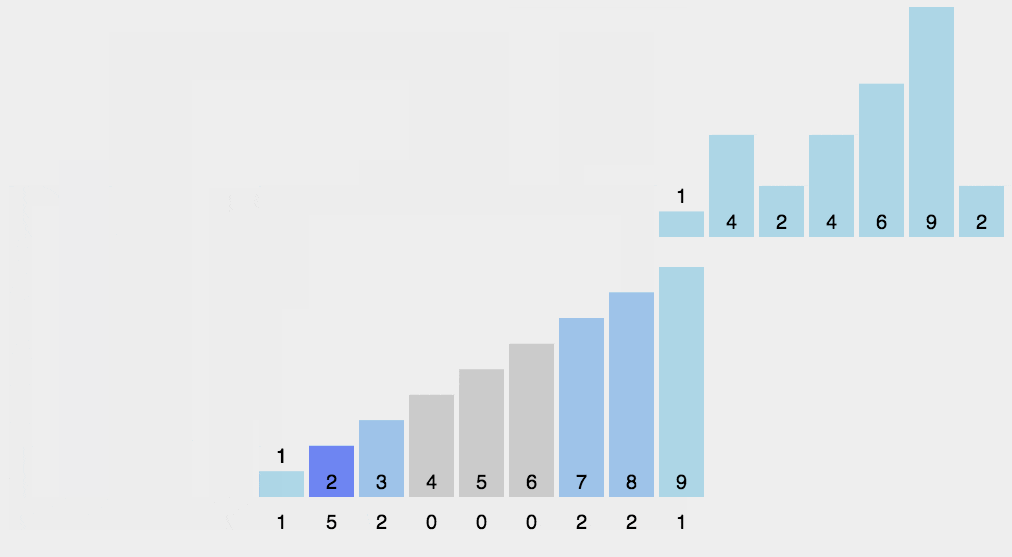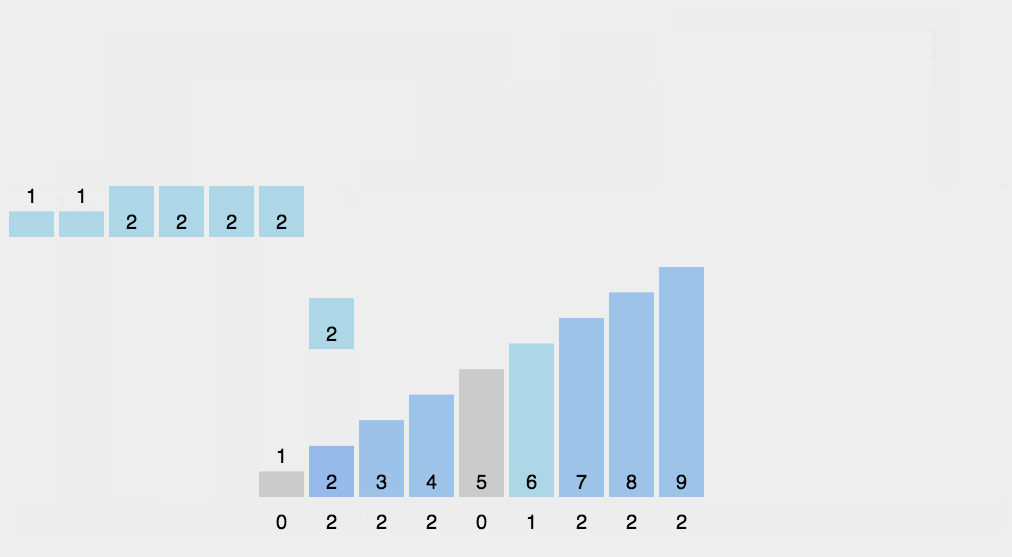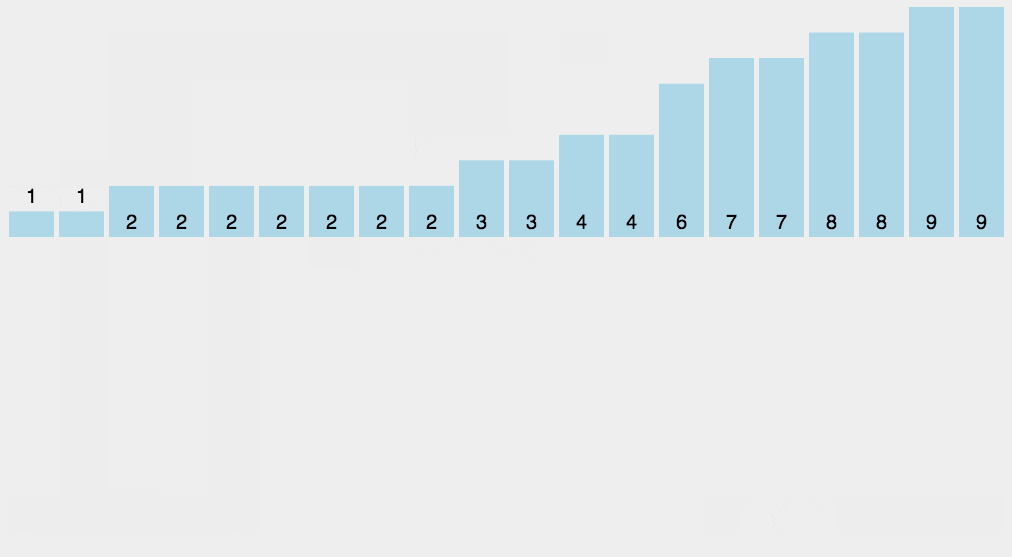
def countSort(arr):
output = [0 for i in range(256)]
count = [0 for i in range(256)]
ans = ["" for _ in arr]
for i in arr:
count[ord(i)] += 1
for i in range(256):
count[i] += count[i-1]
for i in range(len(arr)):
output[count[ord(arr[i])]-1] = arr[i]
count[ord(arr[i])] -= 1
for i in range(len(arr)):
ans[i] = output[i]
return ans
arr = "wwwnowcodercom"
ans = countSort(arr)
print("字符数组排序 %s" %("".join(ans)))运行结果：
字符数组排序 ccdemnooorwwww
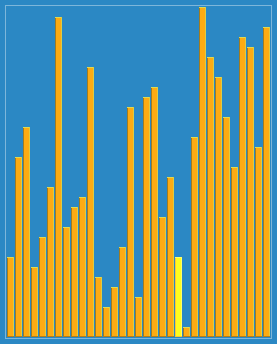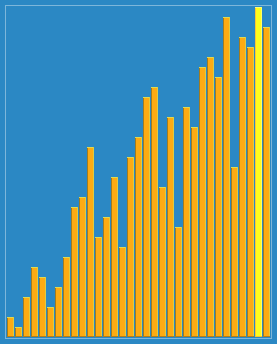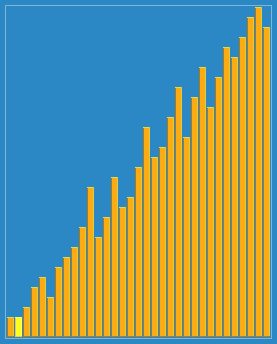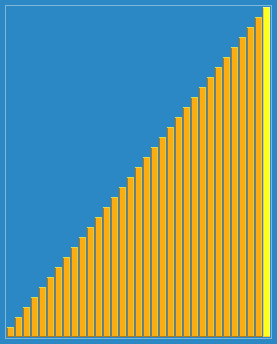
希尔排序：也称递减增量排序算法，是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
希尔排序的基本思想是：先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录"基本有序"时，再对全体记录进行依次直接插入排序。
def shellSort(arr):
n = len(arr)
gap = int(n/2)
while gap > 0:
for i in range(gap, n):
temp = arr[i]
j = i
while j >= gap and arr[j-gap] > temp:
arr[j] = arr[j-gap]
j -= gap
arr[j] = temp
gap = int(gap/2)
return arr
arr = [12, 34, 54, 2, 3, 2, 5]
print("排序前:")
print(arr)
print("排序后:")
print(shellSort(arr))运行结果：
排序前:
[12, 34, 54, 2, 3, 2, 5]
排序后:
[2, 2, 3, 5, 12, 34, 54]
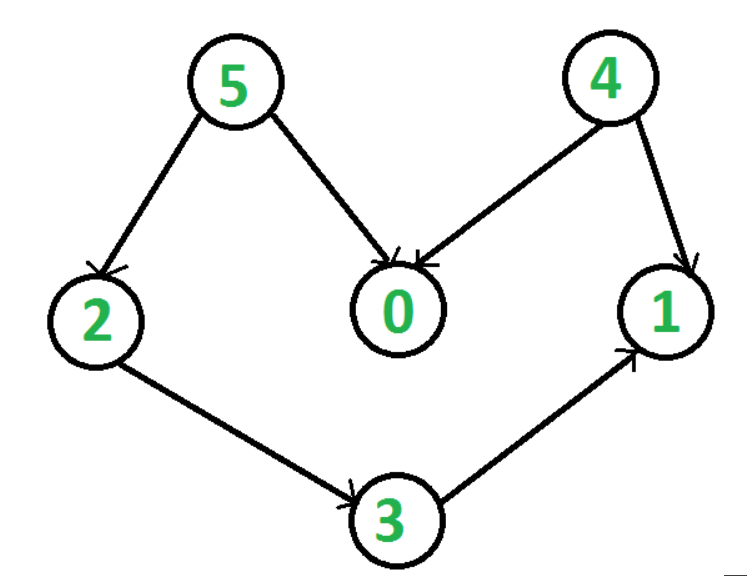
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。拓扑排序是一种将集合上的偏序转换为全序的操作。
在图论中，由一个有向无环图的顶点组成的序列，当且仅当满足下列条件时，称为该图的一个拓扑排序（英语：Topological sorting）：
每个顶点出现且只出现一次；若A在序列中排在B的前面，则在图中不存在从B到A的路径。
from collections import defaultdict
class Graph:
def __init__(self, vertices):
self.graph = defaultdict(list)
self.V = vertices
def addEdge(self, u, v):
self.graph[u].append(v)
def topologicalSortUtil(self, v, visited, stack):
visited[v] = True
for i in self.graph[v]:
if visited[i] == False:
self.topologicalSortUtil(i, visited, stack)
stack.insert(0,v)
def topologicalSort(self):
visited = [False]*self.V
stack = []
for i in range(self.V):
if visited[i] == False:
self.topologicalSortUtil(i, visited, stack)
print(stack)
g= Graph(6)
g.addEdge(5, 2)
g.addEdge(5, 0)
g.addEdge(4, 0)
g.addEdge(4, 1)
g.addEdge(2, 3)
g.addEdge(3, 1)
print("拓扑排序结果：")
g.topologicalSort()运行结果：
拓扑排序结果：
[5, 4, 2, 3, 1, 0]
위 내용은 Python 검색 및 정렬 알고리즘 예제 코드 분석의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
![[웹 프런트엔드] Node.js 빠른 시작](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
