비트 연산을 사용하여 Java에서 곱셈을 구현하는 방법

소수 곱셈

예를 들어 26 * 15, 곱셈 연산을 할 때 보통 이렇게 계산하는데, 먼저 5에 6을 곱합니다. 30을 얻으려면 0을 쓰고 3을 따로 둔 다음 5에 2 를 곱하세요. >10에 아래에 적힌 이전 3을 더하고 5를 계산한 후 130을 구한 다음 1을 계산합니다. 를 입력하고 각각 6과 2를 곱합니다. 결과 26를 기록한 다음 130을 기록합니다. 26(잘못 정렬됨)은 390을 나타냅니다. 26 * 15，在进行乘法操作时，我们一般这样算，先用5乘以6得到30，把0写下把3记在一边，再用5乘以2得到10再加上之前的3写在下面，得到130；计算完5再计算1分别乘以6和2把得到的结果26记在下面，然后把130和26相加(有错位)得到390。

二进制相乘

看完了十进制的相乘，再来看下二进制的相乘，基本原理是一样的，也是以十字相乘法为例，计算 5 * 7。

5的二进制为101，7的二进制为111，来看下二进制的十字相乘法。

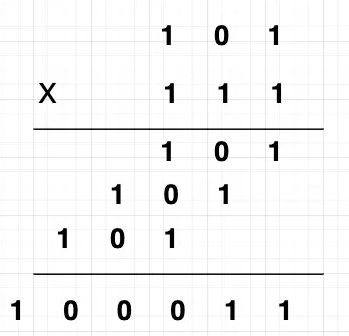
可以看到二进制为101和二进制111用传统的方式来计算，得到的结果为100011，而二进制100011对应的十进制为35。
所以说，在计算的过程中，十进制和二进制的计算方式是一样的，当然这里就不进行举例和证明了。

思路分析

既然计算过程有了，那么怎么样用代码来实现呢？

我们再来看下上图中二进制的计算过程：

• 先用二进制111的最后一位1 乘上 101 得到 101。

• 再用二进制111的倒数第2位1 乘上 101 得到 101。

• 再用二进制111的倒数第3位1 乘上 101 得到 101。

• 得到的三个101进行二进制相加，得到 100011。

注意，第2步和第3步得到的结果101都往前挪了一位，相当于1010和10100，也就是最后相加的计算为：10100 + 1010 + 101 = 100011。

再来看得到最终相加的计算10100 + 1010 + 101 = 100011，也就是只要我们找到如何把数据转换为几位数的相加就可以了，因为之前已经实现了如何用位运算实现加法操作。

这三个数101、1010、10100的数量刚好与二进制111的个数相同，也就是二进制(上图下面那个乘数111)有几位就会产生几个数相加，如果是与11111相乘就会产生5个数相加。

再来看数据之前的关系：

• 第一次相乘结果：101 = 101 + 0

• 第二次相乘结果：1111 = 101

• 第三次相乘结果：100011 = 101

从这里我们可以看到，每计算一次，101只需要向左移一次再加上上一次的计算结果就可以了。

那么，怎么知道要左移多少次呢？从这里例子中看，111每次计算后，向右移动一次，101也跟着向左移动一次，直到111

Binary 곱셈

십진법 곱셈을 읽은 후 기본 원리는 동일합니다. 5 * 7을 계산하기 위해 교차 곱셈 방법도 살펴보겠습니다.

5의 이진법은 101이고, 7의 이진법은 111임을 살펴보겠습니다. 이진 교차 곱셈 법칙.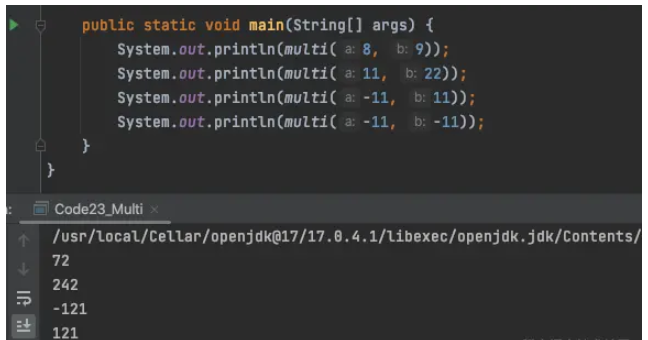

You 이진수 101 및 이진수 111가 기존 방식으로 계산되어 결과는 100011인 반면 이진수 100011를 볼 수 있습니다. > 해당 십진수 표기법은 35입니다.
그래서 계산 과정에서 십진법과 이진법의 계산 방법은 동일합니다. 물론 여기서는 예와 증명을 제시하지 않습니다.

🎜사고 분석🎜🎜이제 계산 과정은 끝났으니 코드로 어떻게 구현할까요? 🎜🎜위 그림에서 이진수 계산 과정을 살펴보겠습니다. 🎜

• 🎜먼저 이진수 1111을 사용합니다. /code> 101을 곱하여 101을 얻습니다. 🎜
• 🎜그런 다음 이진수 111의 마지막 두 번째 숫자 1에 101를 곱하여 101을 얻습니다. 코드코드>. 🎜
• 🎜그런 다음 이진수 111의 마지막 세 번째 숫자 1에 101를 곱하여 101을 얻습니다. 코드코드>. 🎜
• 🎜얻은 101 3개를 바이너리로 더해 100011를 얻습니다. 🎜

🎜 2 및 3 단계에서 얻은 결과 101가 비트 앞으로 이동되었습니다. 1010 및 10100으로, 즉 최종 덧셈 계산은 10100 + 1010 + 101 = 100011입니다. 🎜🎜최종 덧셈 10100 + 1010 + 101 = 100011의 계산을 살펴보겠습니다. 즉, 데이터를 여러 자리의 덧셈으로 변환하는 방법만 찾는다면 충분합니다. 비트 연산을 이용한 덧셈 연산을 구현하는 방법 이전에 구현되었기 때문입니다. 🎜🎜이 세 숫자 101, 1010, 10100의 숫자는 이진수 111의 숫자와 정확히 같습니다. 즉, 이진수 개수(위 그림 하단의 승수 111)에 11111을 곱하면 여러 개의 숫자가 생성됩니다. code>, <code> 5 숫자가 더해집니다. 🎜🎜데이터 이전의 관계를 살펴보겠습니다. 🎜

• 🎜첫 번째 곱셈 결과: 101 = 101 + 0🎜
• 🎜두 번째 곱셈 결과: 1111 = 101 🎜
• 🎜세 번째 곱셈 결과: 100011 = 101 🎜

🎜 여기에서 모든 계산이 101 왼쪽으로만 이동하면 된다는 것을 알 수 있습니다. 한 번 클릭하고 마지막 계산 결과를 추가합니다. 🎜🎜그렇다면 왼쪽으로 몇 번이나 이동하는지 어떻게 알 수 있나요? 여기 예에서 111는 각 계산 후 오른쪽으로 한 번씩 이동하고, 111만 남을 때까지 101도 왼쪽으로 한 번씩 이동합니다. 마지막 숫자는 계산을 중지하세요. 🎜🎜코드 구현🎜🎜위 아이디어에 따라 코드를 구현해 보겠습니다.🎜

// 用位运算实现加法
public static int add(int a, int b) {
    int sum = 0;
    while (b != 0) {
        sum = a ^ b;
        b = (a & b) << 1;
        a = sum;
    }
    return sum;
}

// 用位运算实现减法
public static int multi(int a, int b) {
    int res = 0;
    while (b != 0) {
        if ((b & 1) != 0) {
            res = add(res, a);
        }
        a <<= 1;
        b >>>= 1;
    }
    return res;
}

🎜코드를 실행하고 결과를 확인하세요.🎜🎜🎜🎜🎜계산이 정확하고 음수도 지원되는 것을 확인할 수 있습니다. 🎜

위 내용은 비트 연산을 사용하여 Java에서 곱셈을 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!