Python을 기반으로 단안 3D 재구성을 구현하는 방법
1. 단안 3차원 재구성 개요
물체 세계의 물체는 3차원이지만, 우리가 얻는 이미지는 2차원이지만, 우리는 이 2차원 이미지로부터 대상의 3차원 정보를 인지할 수 있습니다. 차원적인 이미지. 3차원 재구성 기술은 영상을 일정한 방식으로 처리해 컴퓨터가 인식할 수 있는 3차원 정보를 얻어 대상을 분석하는 기술이다. 단안 3D 재구성은 단일 카메라의 움직임을 기반으로 양안 시력을 시뮬레이션하여 공간에 있는 물체의 3차원 시각 정보를 얻습니다. 단안은 단일 카메라를 의미합니다.
2. 구현 과정
객체의 단안 3D 재구성 과정에서 관련 운영 환경은 다음과 같습니다:
matplotlib 3.3.4
numpy 1.19.5
opencv-contrib-python 3.4.2.16
opencv- python 3.4.2.16
pillow 8.2.0
python 3.6.2
재구성에는 주로 다음 단계가 포함됩니다.
(1) 카메라 보정
(2) 이미지 특징 추출 및 매칭
(3) 3차원 재구성
다음으로 각 단계의 구체적인 구현을 자세히 살펴보겠습니다.
(1) 카메라 보정
휴대폰 카메라, 디지털 카메라, 기능성 모듈 카메라, 등등. 각 카메라의 매개변수는 다릅니다. 즉, 카메라로 촬영한 사진의 해상도, 모드 등이 다릅니다. 물체의 3차원 재구성을 수행할 때 카메라의 매트릭스 매개변수를 미리 모른다고 가정합니다. 그런 다음 카메라의 매트릭스 매개변수를 계산해야 합니다. 이 단계를 카메라 보정이라고 합니다. 카메라 보정의 관련 원리는 소개하지 않겠습니다. 인터넷에서 많은 사람들이 자세히 설명했습니다. 캘리브레이션의 구체적인 구현은 다음과 같습니다.
def camera_calibration(ImagePath):
# 循环中断
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
# 棋盘格尺寸（棋盘格的交叉点的个数）
row = 11
column = 8
objpoint = np.zeros((row * column, 3), np.float32)
objpoint[:, :2] = np.mgrid[0:row, 0:column].T.reshape(-1, 2)
objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.
batch_images = glob.glob(ImagePath + '/*.jpg')
for i, fname in enumerate(batch_images):
img = cv2.imread(batch_images[i])
imgGray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# find chess board corners
ret, corners = cv2.findChessboardCorners(imgGray, (row, column), None)
# if found, add object points, image points (after refining them)
if ret:
objpoints.append(objpoint)
corners2 = cv2.cornerSubPix(imgGray, corners, (11, 11), (-1, -1), criteria)
imgpoints.append(corners2)
# Draw and display the corners
img = cv2.drawChessboardCorners(img, (row, column), corners2, ret)
cv2.imwrite('Checkerboard_Image/Temp_JPG/Temp_' + str(i) + '.jpg', img)
print("成功提取:", len(batch_images), "张图片角点！")
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, imgGray.shape[::-1], None, None)그 중 cv2.calibrateCamera 함수로 얻은 mtx 행렬이 K 행렬입니다.
해당 매개변수를 수정하고 보정을 완료한 후 체커보드의 꼭지점이 성공적으로 추출되었는지 확인하기 위해 체커판의 꼭지점 이미지를 출력할 수 있습니다. 출력된 꼭지점 이미지는 다음과 같습니다.
그림 1: 체커보드 모서리 점 추출
(2) 이미지 특징 추출 및 매칭
전체 3차원 재구성 프로세스에서 이 단계는 가장 중요하고 가장 복잡한 단계로 이미지 특징 추출의 품질이 최종 재구성을 결정합니다. 효과.
이미지 특징점 추출 알고리즘 중에는 SIFT 알고리즘, SURF 알고리즘, ORB 알고리즘이라는 세 가지 일반적으로 사용되는 알고리즘이 있습니다. 이 단계에서는 종합적인 분석과 비교를 통해 SURF 알고리즘을 사용하여 이미지의 특징점을 추출합니다. 세 가지 알고리즘의 특징점 추출 효과를 비교하고 싶으시면 온라인으로 검색해 보시고 여기서는 하나씩 비교하지 않겠습니다. 구체적인 구현은 다음과 같습니다.
def epipolar_geometric(Images_Path, K):
IMG = glob.glob(Images_Path)
img1, img2 = cv2.imread(IMG[0]), cv2.imread(IMG[1])
img1_gray = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
img2_gray = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)
# Initiate SURF detector
SURF = cv2.xfeatures2d_SURF.create()
# compute keypoint & descriptions
keypoint1, descriptor1 = SURF.detectAndCompute(img1_gray, None)
keypoint2, descriptor2 = SURF.detectAndCompute(img2_gray, None)
print("角点数量：", len(keypoint1), len(keypoint2))
# Find point matches
bf = cv2.BFMatcher(cv2.NORM_L2, crossCheck=True)
matches = bf.match(descriptor1, descriptor2)
print("匹配点数量：", len(matches))
src_pts = np.asarray([keypoint1[m.queryIdx].pt for m in matches])
dst_pts = np.asarray([keypoint2[m.trainIdx].pt for m in matches])
# plot
knn_image = cv2.drawMatches(img1_gray, keypoint1, img2_gray, keypoint2, matches[:-1], None, flags=2)
image_ = Image.fromarray(np.uint8(knn_image))
image_.save("MatchesImage.jpg")
# Constrain matches to fit homography
retval, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, 100.0)
# We select only inlier points
points1 = src_pts[mask.ravel() == 1]
points2 = dst_pts[mask.ravel() == 1]에서 찾은 특징점은 다음과 같습니다.
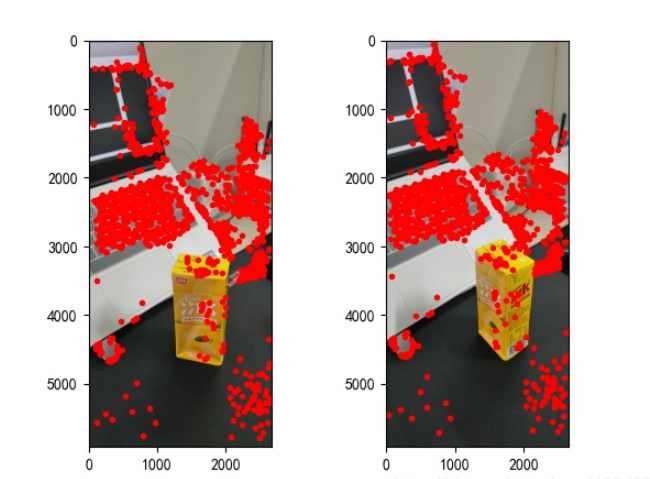
그림 2: 특징점 추출
(3) 3차원 재구성
그림의 특징점을 찾은 후 서로 일치시키면 3차원 재구성을 시작할 수 있습니다. 구체적인 구현은 다음과 같습니다:
points1 = cart2hom(points1.T)
points2 = cart2hom(points2.T)
# plot
fig, ax = plt.subplots(1, 2)
ax[0].autoscale_view('tight')
ax[0].imshow(cv2.cvtColor(img1, cv2.COLOR_BGR2RGB))
ax[0].plot(points1[0], points1[1], 'r.')
ax[1].autoscale_view('tight')
ax[1].imshow(cv2.cvtColor(img2, cv2.COLOR_BGR2RGB))
ax[1].plot(points2[0], points2[1], 'r.')
plt.savefig('MatchesPoints.jpg')
fig.show()
#
points1n = np.dot(np.linalg.inv(K), points1)
points2n = np.dot(np.linalg.inv(K), points2)
E = compute_essential_normalized(points1n, points2n)
print('Computed essential matrix:', (-E / E[0][1]))
P1 = np.array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
P2s = compute_P_from_essential(E)
ind = -1
for i, P2 in enumerate(P2s):
# Find the correct camera parameters
d1 = reconstruct_one_point(points1n[:, 0], points2n[:, 0], P1, P2)
# Convert P2 from camera view to world view
P2_homogenous = np.linalg.inv(np.vstack([P2, [0, 0, 0, 1]]))
d2 = np.dot(P2_homogenous[:3, :4], d1)
if d1[2] > 0 and d2[2] > 0:
ind = i
P2 = np.linalg.inv(np.vstack([P2s[ind], [0, 0, 0, 1]]))[:3, :4]
Points3D = linear_triangulation(points1n, points2n, P1, P2)
fig = plt.figure()
fig.suptitle('3D reconstructed', fontsize=16)
ax = fig.gca(projection='3d')
ax.plot(Points3D[0], Points3D[1], Points3D[2], 'b.')
ax.set_xlabel('x axis')
ax.set_ylabel('y axis')
ax.set_zlabel('z axis')
ax.view_init(elev=135, azim=90)
plt.savefig('Reconstruction.jpg')
plt.show()재구성 효과는 다음과 같습니다(효과는 평균입니다):
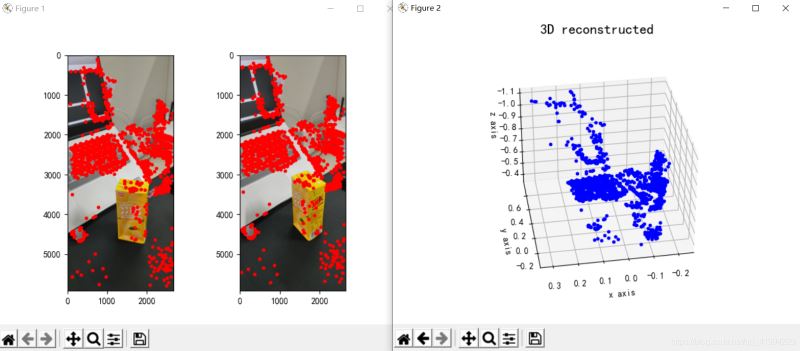
그림 3: 3차원 재구성
III. 결론
재구성 결과에서 단안의 3차원 재구성 효과는 평균적인 것으로 생각됩니다.
(1) 사진 촬영 형식. 단안 3D 재구성 작업을 수행하는 경우 사진을 찍을 때 카메라를 평행하게 계속 움직이는 것이 가장 좋으며 정면에서 사진을 찍는 것이 가장 좋습니다. 즉, 특정 각도나 특정 각도로 사진을 찍지 마십시오.
(2) 사진 촬영 시 주변 환경의 간섭을 받습니다. 관련 없는 물체의 간섭을 줄이려면 단일 촬영 위치를 선택하는 것이 가장 좋습니다.
(3) 촬영 광원 문제. 선택한 사진 위치는 적절한 밝기를 보장해야 하며(광원이 표준을 충족하는지 확인하려면 특정 상황을 테스트해야 함), 카메라를 이동할 때 광원이 이전 순간과 이번 순간 사이에서 일치하는지 확인해야 합니다. 순간.
사실 단안 3D 재구성의 성능은 일반적으로 모든 조건이 최적일 때에도 결과적인 재구성 효과가 그리 좋지 않습니다. 아니면 쌍안 3D 재구성을 사용하는 것을 고려할 수도 있습니다. 단안의 효과보다 확실히 양안 3D 재구성의 효과가 더 좋습니다. 하하. 실제로 작업은 복잡하지 않습니다. 가장 까다로운 부분은 두 카메라를 촬영하고 보정하는 것입니다. 다른 측면은 비교적 쉽습니다.
4.코드
import cv2
import json
import numpy as np
import glob
from PIL import Image
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def cart2hom(arr):
""" Convert catesian to homogenous points by appending a row of 1s
:param arr: array of shape (num_dimension x num_points)
:returns: array of shape ((num_dimension+1) x num_points)
"""
if arr.ndim == 1:
return np.hstack([arr, 1])
return np.asarray(np.vstack([arr, np.ones(arr.shape[1])]))
def compute_P_from_essential(E):
""" Compute the second camera matrix (assuming P1 = [I 0])
from an essential matrix. E = [t]R
:returns: list of 4 possible camera matrices.
"""
U, S, V = np.linalg.svd(E)
# Ensure rotation matrix are right-handed with positive determinant
if np.linalg.det(np.dot(U, V)) < 0:
V = -V
# create 4 possible camera matrices (Hartley p 258)
W = np.array([[0, -1, 0], [1, 0, 0], [0, 0, 1]])
P2s = [np.vstack((np.dot(U, np.dot(W, V)).T, U[:, 2])).T,
np.vstack((np.dot(U, np.dot(W, V)).T, -U[:, 2])).T,
np.vstack((np.dot(U, np.dot(W.T, V)).T, U[:, 2])).T,
np.vstack((np.dot(U, np.dot(W.T, V)).T, -U[:, 2])).T]
return P2s
def correspondence_matrix(p1, p2):
p1x, p1y = p1[:2]
p2x, p2y = p2[:2]
return np.array([
p1x * p2x, p1x * p2y, p1x,
p1y * p2x, p1y * p2y, p1y,
p2x, p2y, np.ones(len(p1x))
]).T
return np.array([
p2x * p1x, p2x * p1y, p2x,
p2y * p1x, p2y * p1y, p2y,
p1x, p1y, np.ones(len(p1x))
]).T
def scale_and_translate_points(points):
""" Scale and translate image points so that centroid of the points
are at the origin and avg distance to the origin is equal to sqrt(2).
:param points: array of homogenous point (3 x n)
:returns: array of same input shape and its normalization matrix
"""
x = points[0]
y = points[1]
center = points.mean(axis=1) # mean of each row
cx = x - center[0] # center the points
cy = y - center[1]
dist = np.sqrt(np.power(cx, 2) + np.power(cy, 2))
scale = np.sqrt(2) / dist.mean()
norm3d = np.array([
[scale, 0, -scale * center[0]],
[0, scale, -scale * center[1]],
[0, 0, 1]
])
return np.dot(norm3d, points), norm3d
def compute_image_to_image_matrix(x1, x2, compute_essential=False):
""" Compute the fundamental or essential matrix from corresponding points
(x1, x2 3*n arrays) using the 8 point algorithm.
Each row in the A matrix below is constructed as
[x'*x, x'*y, x', y'*x, y'*y, y', x, y, 1]
"""
A = correspondence_matrix(x1, x2)
# compute linear least square solution
U, S, V = np.linalg.svd(A)
F = V[-1].reshape(3, 3)
# constrain F. Make rank 2 by zeroing out last singular value
U, S, V = np.linalg.svd(F)
S[-1] = 0
if compute_essential:
S = [1, 1, 0] # Force rank 2 and equal eigenvalues
F = np.dot(U, np.dot(np.diag(S), V))
return F
def compute_normalized_image_to_image_matrix(p1, p2, compute_essential=False):
""" Computes the fundamental or essential matrix from corresponding points
using the normalized 8 point algorithm.
:input p1, p2: corresponding points with shape 3 x n
:returns: fundamental or essential matrix with shape 3 x 3
"""
n = p1.shape[1]
if p2.shape[1] != n:
raise ValueError('Number of points do not match.')
# preprocess image coordinates
p1n, T1 = scale_and_translate_points(p1)
p2n, T2 = scale_and_translate_points(p2)
# compute F or E with the coordinates
F = compute_image_to_image_matrix(p1n, p2n, compute_essential)
# reverse preprocessing of coordinates
# We know that P1' E P2 = 0
F = np.dot(T1.T, np.dot(F, T2))
return F / F[2, 2]
def compute_fundamental_normalized(p1, p2):
return compute_normalized_image_to_image_matrix(p1, p2)
def compute_essential_normalized(p1, p2):
return compute_normalized_image_to_image_matrix(p1, p2, compute_essential=True)
def skew(x):
""" Create a skew symmetric matrix *A* from a 3d vector *x*.
Property: np.cross(A, v) == np.dot(x, v)
:param x: 3d vector
:returns: 3 x 3 skew symmetric matrix from *x*
"""
return np.array([
[0, -x[2], x[1]],
[x[2], 0, -x[0]],
[-x[1], x[0], 0]
])
def reconstruct_one_point(pt1, pt2, m1, m2):
"""
pt1 and m1 * X are parallel and cross product = 0
pt1 x m1 * X = pt2 x m2 * X = 0
"""
A = np.vstack([
np.dot(skew(pt1), m1),
np.dot(skew(pt2), m2)
])
U, S, V = np.linalg.svd(A)
P = np.ravel(V[-1, :4])
return P / P[3]
def linear_triangulation(p1, p2, m1, m2):
"""
Linear triangulation (Hartley ch 12.2 pg 312) to find the 3D point X
where p1 = m1 * X and p2 = m2 * X. Solve AX = 0.
:param p1, p2: 2D points in homo. or catesian coordinates. Shape (3 x n)
:param m1, m2: Camera matrices associated with p1 and p2. Shape (3 x 4)
:returns: 4 x n homogenous 3d triangulated points
"""
num_points = p1.shape[1]
res = np.ones((4, num_points))
for i in range(num_points):
A = np.asarray([
(p1[0, i] * m1[2, :] - m1[0, :]),
(p1[1, i] * m1[2, :] - m1[1, :]),
(p2[0, i] * m2[2, :] - m2[0, :]),
(p2[1, i] * m2[2, :] - m2[1, :])
])
_, _, V = np.linalg.svd(A)
X = V[-1, :4]
res[:, i] = X / X[3]
return res
def writetofile(dict, path):
for index, item in enumerate(dict):
dict[item] = np.array(dict[item])
dict[item] = dict[item].tolist()
js = json.dumps(dict)
with open(path, 'w') as f:
f.write(js)
print("参数已成功保存到文件")
def readfromfile(path):
with open(path, 'r') as f:
js = f.read()
mydict = json.loads(js)
print("参数读取成功")
return mydict
def camera_calibration(SaveParamPath, ImagePath):
# 循环中断
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
# 棋盘格尺寸
row = 11
column = 8
objpoint = np.zeros((row * column, 3), np.float32)
objpoint[:, :2] = np.mgrid[0:row, 0:column].T.reshape(-1, 2)
objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.
batch_images = glob.glob(ImagePath + '/*.jpg')
for i, fname in enumerate(batch_images):
img = cv2.imread(batch_images[i])
imgGray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# find chess board corners
ret, corners = cv2.findChessboardCorners(imgGray, (row, column), None)
# if found, add object points, image points (after refining them)
if ret:
objpoints.append(objpoint)
corners2 = cv2.cornerSubPix(imgGray, corners, (11, 11), (-1, -1), criteria)
imgpoints.append(corners2)
# Draw and display the corners
img = cv2.drawChessboardCorners(img, (row, column), corners2, ret)
cv2.imwrite('Checkerboard_Image/Temp_JPG/Temp_' + str(i) + '.jpg', img)
print("成功提取:", len(batch_images), "张图片角点！")
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, imgGray.shape[::-1], None, None)
dict = {'ret': ret, 'mtx': mtx, 'dist': dist, 'rvecs': rvecs, 'tvecs': tvecs}
writetofile(dict, SaveParamPath)
meanError = 0
for i in range(len(objpoints)):
imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
error = cv2.norm(imgpoints[i], imgpoints2, cv2.NORM_L2) / len(imgpoints2)
meanError += error
print("total error: ", meanError / len(objpoints))
def epipolar_geometric(Images_Path, K):
IMG = glob.glob(Images_Path)
img1, img2 = cv2.imread(IMG[0]), cv2.imread(IMG[1])
img1_gray = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
img2_gray = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)
# Initiate SURF detector
SURF = cv2.xfeatures2d_SURF.create()
# compute keypoint & descriptions
keypoint1, descriptor1 = SURF.detectAndCompute(img1_gray, None)
keypoint2, descriptor2 = SURF.detectAndCompute(img2_gray, None)
print("角点数量：", len(keypoint1), len(keypoint2))
# Find point matches
bf = cv2.BFMatcher(cv2.NORM_L2, crossCheck=True)
matches = bf.match(descriptor1, descriptor2)
print("匹配点数量：", len(matches))
src_pts = np.asarray([keypoint1[m.queryIdx].pt for m in matches])
dst_pts = np.asarray([keypoint2[m.trainIdx].pt for m in matches])
# plot
knn_image = cv2.drawMatches(img1_gray, keypoint1, img2_gray, keypoint2, matches[:-1], None, flags=2)
image_ = Image.fromarray(np.uint8(knn_image))
image_.save("MatchesImage.jpg")
# Constrain matches to fit homography
retval, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, 100.0)
# We select only inlier points
points1 = src_pts[mask.ravel() == 1]
points2 = dst_pts[mask.ravel() == 1]
points1 = cart2hom(points1.T)
points2 = cart2hom(points2.T)
# plot
fig, ax = plt.subplots(1, 2)
ax[0].autoscale_view('tight')
ax[0].imshow(cv2.cvtColor(img1, cv2.COLOR_BGR2RGB))
ax[0].plot(points1[0], points1[1], 'r.')
ax[1].autoscale_view('tight')
ax[1].imshow(cv2.cvtColor(img2, cv2.COLOR_BGR2RGB))
ax[1].plot(points2[0], points2[1], 'r.')
plt.savefig('MatchesPoints.jpg')
fig.show()
#
points1n = np.dot(np.linalg.inv(K), points1)
points2n = np.dot(np.linalg.inv(K), points2)
E = compute_essential_normalized(points1n, points2n)
print('Computed essential matrix:', (-E / E[0][1]))
P1 = np.array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
P2s = compute_P_from_essential(E)
ind = -1
for i, P2 in enumerate(P2s):
# Find the correct camera parameters
d1 = reconstruct_one_point(points1n[:, 0], points2n[:, 0], P1, P2)
# Convert P2 from camera view to world view
P2_homogenous = np.linalg.inv(np.vstack([P2, [0, 0, 0, 1]]))
d2 = np.dot(P2_homogenous[:3, :4], d1)
if d1[2] > 0 and d2[2] > 0:
ind = i
P2 = np.linalg.inv(np.vstack([P2s[ind], [0, 0, 0, 1]]))[:3, :4]
Points3D = linear_triangulation(points1n, points2n, P1, P2)
return Points3D
def main():
CameraParam_Path = 'CameraParam.txt'
CheckerboardImage_Path = 'Checkerboard_Image'
Images_Path = 'SubstitutionCalibration_Image/*.jpg'
# 计算相机参数
camera_calibration(CameraParam_Path, CheckerboardImage_Path)
# 读取相机参数
config = readfromfile(CameraParam_Path)
K = np.array(config['mtx'])
# 计算3D点
Points3D = epipolar_geometric(Images_Path, K)
# 重建3D点
fig = plt.figure()
fig.suptitle('3D reconstructed', fontsize=16)
ax = fig.gca(projection='3d')
ax.plot(Points3D[0], Points3D[1], Points3D[2], 'b.')
ax.set_xlabel('x axis')
ax.set_ylabel('y axis')
ax.set_zlabel('z axis')
ax.view_init(elev=135, azim=90)
plt.savefig('Reconstruction.jpg')
plt.show()
if __name__ == '__main__':
main()위 내용은 Python을 기반으로 단안 3D 재구성을 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
핫 AI 도구
Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱
AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.
Undress AI Tool
무료로 이미지를 벗다
Clothoff.io
AI 옷 제거제
AI Hentai Generator
AI Hentai를 무료로 생성하십시오.
인기 기사
뜨거운 도구
메모장++7.3.1
사용하기 쉬운 무료 코드 편집기
SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.
스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경
드림위버 CS6
시각적 웹 개발 도구
SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)
뜨거운 주제
7456
15
1376
52
77
11
41
19
14
9
PS가 계속 로딩을 보여주는 이유는 무엇입니까?
Apr 06, 2025 pm 06:39 PM
PS "로드"문제는 자원 액세스 또는 처리 문제로 인한 것입니다. 하드 디스크 판독 속도는 느리거나 나쁘다 : CrystalDiskinfo를 사용하여 하드 디스크 건강을 확인하고 문제가있는 하드 디스크를 교체하십시오. 불충분 한 메모리 : 고해상도 이미지 및 복잡한 레이어 처리에 대한 PS의 요구를 충족시키기 위해 메모리 업그레이드 메모리. 그래픽 카드 드라이버는 구식 또는 손상됩니다. 운전자를 업데이트하여 PS와 그래픽 카드 간의 통신을 최적화하십시오. 파일 경로는 너무 길거나 파일 이름에는 특수 문자가 있습니다. 짧은 경로를 사용하고 특수 문자를 피하십시오. PS 자체 문제 : PS 설치 프로그램을 다시 설치하거나 수리하십시오.
PS가 시작될 때 로딩 문제를 해결하는 방법은 무엇입니까?
Apr 06, 2025 pm 06:36 PM
부팅 할 때 "로드"에 PS가 붙어있는 여러 가지 이유로 인해 발생할 수 있습니다. 손상되거나 충돌하는 플러그인을 비활성화합니다. 손상된 구성 파일을 삭제하거나 바꾸십시오. 불충분 한 메모리를 피하기 위해 불필요한 프로그램을 닫거나 메모리를 업그레이드하십시오. 하드 드라이브 독서 속도를 높이기 위해 솔리드 스테이트 드라이브로 업그레이드하십시오. 손상된 시스템 파일 또는 설치 패키지 문제를 복구하기 위해 PS를 다시 설치합니다. 시작 오류 로그 분석의 시작 과정에서 오류 정보를 봅니다.
PS가 파일을 열 때로드 문제를 해결하는 방법은 무엇입니까?
Apr 06, 2025 pm 06:33 PM
"로드"는 PS에서 파일을 열 때 말더듬이 발생합니다. 그 이유에는 너무 크거나 손상된 파일, 메모리 불충분, 하드 디스크 속도가 느리게, 그래픽 카드 드라이버 문제, PS 버전 또는 플러그인 충돌이 포함될 수 있습니다. 솔루션은 다음과 같습니다. 파일 크기 및 무결성 확인, 메모리 증가, 하드 디스크 업그레이드, 그래픽 카드 드라이버 업데이트, 의심스러운 플러그인 제거 또는 비활성화 및 PS를 다시 설치하십시오. 이 문제는 PS 성능 설정을 점차적으로 확인하고 잘 활용하고 우수한 파일 관리 습관을 개발함으로써 효과적으로 해결할 수 있습니다.
PS 페더 링은 어떻게 전환의 부드러움을 제어합니까?
Apr 06, 2025 pm 07:33 PM
깃털 통제의 열쇠는 점진적인 성격을 이해하는 것입니다. PS 자체는 그라디언트 곡선을 직접 제어하는 옵션을 제공하지 않지만 여러 깃털, 일치하는 마스크 및 미세 선택으로 반경 및 구배 소프트를 유연하게 조정하여 자연스럽게 전이 효과를 달성 할 수 있습니다.
설치 후 MySQL을 사용하는 방법
Apr 08, 2025 am 11:48 AM
이 기사는 MySQL 데이터베이스의 작동을 소개합니다. 먼저 MySQLworkBench 또는 명령 줄 클라이언트와 같은 MySQL 클라이언트를 설치해야합니다. 1. MySQL-Uroot-P 명령을 사용하여 서버에 연결하고 루트 계정 암호로 로그인하십시오. 2. CreateABase를 사용하여 데이터베이스를 작성하고 데이터베이스를 선택하십시오. 3. CreateTable을 사용하여 테이블을 만들고 필드 및 데이터 유형을 정의하십시오. 4. InsertInto를 사용하여 데이터를 삽입하고 데이터를 쿼리하고 업데이트를 통해 데이터를 업데이트하고 DELETE를 통해 데이터를 삭제하십시오. 이러한 단계를 마스터하고 일반적인 문제를 처리하는 법을 배우고 데이터베이스 성능을 최적화하면 MySQL을 효율적으로 사용할 수 있습니다.
PS 페더 링을 설정하는 방법?
Apr 06, 2025 pm 07:36 PM
PS 페더 링은 이미지 가장자리 블러 효과로, 가장자리 영역에서 픽셀의 가중 평균에 의해 달성됩니다. 깃털 반경을 설정하면 흐림 정도를 제어 할 수 있으며 값이 클수록 흐려집니다. 반경을 유연하게 조정하면 이미지와 요구에 따라 효과를 최적화 할 수 있습니다. 예를 들어, 캐릭터 사진을 처리 할 때 더 작은 반경을 사용하여 세부 사항을 유지하고 더 큰 반경을 사용하여 예술을 처리 할 때 흐릿한 느낌을줍니다. 그러나 반경이 너무 커서 가장자리 세부 사항을 쉽게 잃을 수 있으며 너무 작아 효과는 분명하지 않습니다. 깃털 효과는 이미지 해상도의 영향을받으며 이미지 이해 및 효과 파악에 따라 조정해야합니다.
MySQL 설치 후 데이터베이스 성능을 최적화하는 방법
Apr 08, 2025 am 11:36 AM
MySQL 성능 최적화는 설치 구성, 인덱싱 및 쿼리 최적화, 모니터링 및 튜닝의 세 가지 측면에서 시작해야합니다. 1. 설치 후 innodb_buffer_pool_size 매개 변수와 같은 서버 구성에 따라 my.cnf 파일을 조정해야합니다. 2. 과도한 인덱스를 피하기 위해 적절한 색인을 작성하고 Execution 명령을 사용하여 실행 계획을 분석하는 것과 같은 쿼리 문을 최적화합니다. 3. MySQL의 자체 모니터링 도구 (showprocesslist, showstatus)를 사용하여 데이터베이스 건강을 모니터링하고 정기적으로 백업 및 데이터베이스를 구성하십시오. 이러한 단계를 지속적으로 최적화함으로써 MySQL 데이터베이스의 성능을 향상시킬 수 있습니다.
MySQL은 지불해야합니다
Apr 08, 2025 pm 05:36 PM
MySQL에는 무료 커뮤니티 버전과 유료 엔터프라이즈 버전이 있습니다. 커뮤니티 버전은 무료로 사용 및 수정할 수 있지만 지원은 제한되어 있으며 안정성이 낮은 응용 프로그램에 적합하며 기술 기능이 강합니다. Enterprise Edition은 안정적이고 신뢰할 수있는 고성능 데이터베이스가 필요하고 지원 비용을 기꺼이 지불하는 응용 프로그램에 대한 포괄적 인 상업적 지원을 제공합니다. 버전을 선택할 때 고려 된 요소에는 응용 프로그램 중요도, 예산 책정 및 기술 기술이 포함됩니다. 완벽한 옵션은없고 가장 적합한 옵션 만 있으므로 특정 상황에 따라 신중하게 선택해야합니다.
