mysql 데이터베이스에서 Decimal 유형을 사용하는 방법

1 배경

수량, 무게, 가격 등을 계산하는 등 데이터베이스에서 숫자 연산은 매우 일반적인 요구 사항입니다. 다양한 요구 사항을 충족하기 위해 데이터베이스 시스템은 일반적으로 정확한 숫자 유형과 대략적인 숫자 유형을 지원합니다. 숫자 유형에는 int, 소수 등이 포함됩니다. 이러한 유형의 소수점 위치는 계산 과정에서 고정되며 결과와 동작은 상대적으로 예측 가능합니다. 이 문제는 돈과 관련된 경우 특히 중요하므로 일부 데이터베이스는 특수한 돈 유형을 구현합니다. . 근사 숫자 유형에는 float, double 등이 있으며 이러한 숫자의 정밀도는 부동입니다.

2 Decimal 유형의 사용

십진법의 사용은 대부분의 데이터베이스에서 유사하게 소개됩니다. .

2.1 설명 Decimal

float 및 double과 달리 십진수는 생성 시 정밀도를 설명하는 두 개의 숫자, 즉 정밀도와 소수점 이하 자릿수를 지정해야 합니다. 정수와 소수 부분을 포함하며 소수점 이하 자릿수는 몇 개의 숫자를 포함합니까? 예를 들어 123.45는 정밀도=5이고 소수점=2인 소수를 빌드할 때 이런 방식으로 정의할 수 있습니다.

2.2 테이블을 만들 때 소수를 정의하세요

테이블을 만들 때 다음과 같이 소수를 정의할 수 있습니다.

create table t(d decimal(5, 2));

2.3 소수 데이터 쓰기

여기에 합법적인 데이터를 삽입할 수 있습니다. 예를 들어

insert into t values(123.45);
insert into t values(123.4);

이때 select * from t를 실행하면

+--------+
| d      |
+--------+
| 123.45 |
| 123.40 |
+--------+

를 얻게 됩니다. 123.4가 123.40이 된다는 점에 유의하세요. 이는 정확한 유형의 특성입니다. d 열의 데이터 각 행에는 scale=2가 필요합니다. 즉, 뒤에 두 자리가 있습니다. 소수점

정밀도와 소수점 정의를 충족하지 않는 데이터를 삽입할 때

insert into t values(1123.45);
ERROR 1264 (22003): Out of range value for column 'd' at row 1
insert into t values(123.456);
Query OK, 1 row affected, 1 warning
show warnings;
+-------+------+----------------------------------------+
| Level | Code | Message                                |
+-------+------+----------------------------------------+
| Note  | 1265 | Data truncated for column 'd' at row 1 |
+-------+------+----------------------------------------+
select * from t;
+--------+
| d      |
+--------+
| 123.46 |
+--------+

1234.5와 유사(정밀도=5 , scale=1과 같은 숫자)는 요구 사항을 충족하는 것처럼 보이지만 실제로는 소수점을 충족해야 합니다. scale=2의 요구 사항이므로 요구 사항을 충족하지 않는 1234.50(정밀도=6, scale=2)이 됩니다.

2.4 계산을 위해 deimcal을 꺼냅니다.

계산된 결과는 정의에 의해 제한되지 않지만 영향을 받습니다. MySQL의 경우 최대 결과는 정밀도=81, 규모=30일 수 있지만 MySQL 십진수의 메모리 형식 및 계산 기능 구현 문제로 인해 이 크기는 모든 상황에서 달성될 수 없습니다. 나중에 자세히 소개하겠습니다.

select d + 9999.999 from t;
+--------------+
| d + 9999.999 |
+--------------+
|    10123.459 |
+--------------+

결과는 정밀도=5, 규모=2의 한계를 뛰어넘었습니다. 기본 규칙은 다음과 같습니다.

1. 추가 /뺄셈/합: 양쪽에 가장 큰 소수를 취함

2. 곱셈: 양쪽에 소수를 더함

3. 나눗셈: 피제수의 소수 + div_precision_increment (데이터베이스 구현에 따라 다름)

3 Decimal type 구현

이 부분에서는 주로 MySQL의 십진수 구현을 소개합니다. 또한 ClickHouse를 비교하여 다양한 시스템에서 십진수 설계 및 구현의 차이점을 살펴보겠습니다.

십진수를 구현하려면 고려해야 할 사항이 있습니다. 다음 문제

1. 정밀도는 얼마나 지원되나요? 그리고 스케일

2. 스케일을 저장할 위치

3. 연속 곱셈이나 나눗셈 중에 스케일이 계속 커지고 정수 부분도 계속 늘어나서 저장된 버퍼가 크기에는 항상 상한선이 있습니다. 이를 어떻게 처리해야 합니까?

4. 나눗셈 결과의 소수점은 어떻게 결정하나요?

5. 소수의 표현 범위와 계산 성능이 충돌합니까?

3.1 MySQL

먼저 MySQL 십진수 관련 데이터 구조를 살펴보겠습니다.

typedef int32 decimal_digit_t;

struct decimal_t {
  int intg, frac, len;
  bool sign;
  decimal_digit_t *buf;
};

MySQL의 십진수는 길이가 len인 십진수_digit_t(int32)의 배열 buf를 사용하여 십진수를 저장할 수 있습니다. Intg는 정수 부분의 자릿수를 나타내고, frac는 소수 부분을 나타냅니다. 부분의 자릿수, sign은 기호를 나타냅니다. 소수 부분과 정수 부분은 별도로 저장해야 하며 하나로 혼합할 수 없습니다. len은 항상 9입니다. 저장 공간의 상한을 나타내는 MySQL 구현과 buf의 실제 유효 부분은 intg 및 frac에 의해 결정됩니다. 예:

// 123.45 decimal(5, 2) 整数部分为 3,  小数部分为 2
decimal_t dec_123_45 = {
  int intg = 3;
  int frac = 2;
  int len = 9;
  bool sign = false;
  decimal_digit_t *buf = {123, 450000000, ...};
};

MySQL은 123.45를 저장하려면 두 개의 십진수_t(int32)를 사용해야 하며 첫 번째는 123입니다. intg=3과 결합하면 정수 부분이 123이고 두 번째 숫자가 450000000(총 9개 숫자)이라는 뜻입니다. 왜냐하면 frac=2이므로 소수 부분이 .45라는 뜻입니다

더 크게 살펴보겠습니다. 예:

// decimal(81, 18) 63 个整数数字, 18 个小数数字, 用满整个 buffer
// 123456789012345678901234567890123456789012345678901234567890123.012345678901234567
decimal_t dec_81_digit = {
  int intg = 63;
  int frac = 18;
  int len = 9;
  bool sign = false;
  buf = {123456789, 12345678, 901234567, 890123456, 789012345, 678901234, 567890123, 12345678, 901234567}
};

이 예에서는 81개의 숫자를 사용하지만 81개의 숫자를 사용할 수 없는 일부 시나리오가 있습니다. 이는 정수와 소수 때문입니다. 부분이 별도로 저장되므로,decimal_digit_t(int32)는 유효한 십진수 하나만 저장할 수 있습니다. 그러나 나머지 부분은 정수 부분으로 사용할 수 없습니다. 예를 들어 소수점은 정수 부분이 62자리이고 소수 부분이 19자리(precision=81, scale=19)인 경우 소수 부분을 사용해야 합니다. 3decimal_digit_t(int32), 정수 부분은 아직 54자리가 남아 있어 62자리를 저장할 수 없습니다. 이 경우 MySQL은 정수 부분에 우선 순위를 부여합니다. 요구 사항을 충족하기 위해 자동으로 소수점 이하 부분을 잘라내고 바꿉니다. 십진수(80, 18)

接下来看看 MySQL 如何在这个数据结构上进行运算. MySQL 通过一系列 decimal_digit_t(int32) 来表示一个较大的 decimal, 其计算也是对这个数组中的各个 decimal_digit_t 分别进行, 如同我们在小学数学计算时是一个数字一个数字地计算, MySQL 会把每个 decimal_digit_t 当作一个数字来进行计算、进位. 由于代码较长, 这里不再对具体的代码进行完整的分析, 仅对代码中核心部分进行分析, 如果感兴趣, 可以直接参考 MySQL 源码 strings/decimal.h 和 strings/decimal.cc 中的 decimal_add, decimal_mul, decimal_div 等代码.

准备步骤

在真正计算前, 还需要做一些准备工作：

1. MySQL 会将数字的个数 ROUND_UP 到 9 的整数倍, 这样后面就可以按照 decimal_digit_t 为单位来进行计算

2. 此外还要针对参与运算的两个 decimal 的具体情况, 计算结果的 precision 和 scale, 如果发现结果的 precision 超过了支持的上限, 那么会按照 decimal_digit_t 为单位减少小数的数字.

3. 在乘法过程中, 如果发生了 2 中的减少行为, 则需要 TRUNCATE 两个运算数, 避免中间结果超出范围.

加法主要步骤

首先, 因为两个数字的 precision 和 scale 可能不相同, 需要做一些准备工作, 将小数点对齐, 然后开始计算, 从最末尾小数开始向高位加, 分为三个步骤：

1. 将小数较多的 decimal 多出的小数数字复制到结果中

2. 将两个 decimal 公共的部分相加

3. 将整数较多的 decimal 多出的整数数字与进位相加到结果中

代码中使用了 stop, stop2 来标记小数点对齐后, 长度不同的数字出现差异的位置.

/* part 1 - max(frac) ... min (frac) */
while (buf1 > stop) *--buf0 = *--buf1;

/* part 2 - min(frac) ... min(intg) */
carry = 0;
while (buf1 > stop2) {
  ADD(*--buf0, *--buf1, *--buf2, carry);
}

/* part 3 - min(intg) ... max(intg) */
buf1 = intg1 > intg2 ? ((stop3 = from1->buf) + intg1 - intg2)
                     : ((stop3 = from2->buf) + intg2 - intg1);
while (buf1 > stop3) {
  ADD(*--buf0, *--buf1, 0, carry);
}

乘法主要步骤

乘法引入了一个新的 dec2, 表示一个 64 bit 的数字, 这是因为两个 decimal_digit_t(int32) 相乘后得到的可能会是一个 64 bit 的数字. 在计算时一定要先把类型转换到 dec2(int64), 再计算, 否则会得到溢出后的错误结果. 乘法与加法不同, 乘法不需要对齐, 例如计算 11.11 5.0, 那么只要计算 111150=55550, 再移动小数点位置就能得到正确结果 55.550

MySQL 实现了一个双重循环将 decimal1 的 每一个 decimal_digit_t 与 decimal2 的每一个 decimal_digit_t 相乘, 得到一个 64 位的 dec2, 其低 32 位是当前的结果, 其高 32 位是进位.

typedef decimal_digit_t dec1;
typedef longlong dec2;

for (buf1 += frac1 - 1; buf1 >= stop1; buf1--, start0--) {
  carry = 0;
  for (buf0 = start0, buf2 = start2; buf2 >= stop2; buf2--, buf0--) {
    dec1 hi, lo;
    dec2 p = ((dec2)*buf1) * ((dec2)*buf2);
    hi = (dec1)(p / DIG_BASE);
    lo = (dec1)(p - ((dec2)hi) * DIG_BASE);
    ADD2(*buf0, *buf0, lo, carry);
    carry += hi;
  }
  if (carry) {
    if (buf0 < to->buf) return E_DEC_OVERFLOW;
    ADD2(*buf0, *buf0, 0, carry);
  }
  for (buf0--; carry; buf0--) {
    if (buf0 < to->buf) return E_DEC_OVERFLOW;
    ADD(*buf0, *buf0, 0, carry);
  }
}

除法主要步骤

除法使用的是 Knuth's Algorithm D, 其基本思路和手动除法也比较类似.

首先使用除数的前两个 decimal_digit_t 组成一个试商因数, 这里使用了一个 norm_factor 来保证数字在不溢出的情况下尽可能扩大, 这是因为 decimal 为了保证精度必须使用整形来进行计算, 数字越大, 得到的结果就越准确. D3: 猜商, 就是用被除数的前两个 decimal_digit_t 除以试商因数 这里如果不乘 norm_factor, 则 start1[1] 和 start2[1] 都不会体现在结果之中.

D4: 将 guess 与除数相乘, 再从被除数中剪掉结果 然后做一些修正, 移动向下一个 decimal_digit_t, 重复这个过程.

想更详细地了解这个算法可以参考 https://skanthak.homepage.t-online.de/division.html

norm2 = (dec1)(norm_factor * start2[0]);
if (likely(len2 > 0)) norm2 += (dec1)(norm_factor * start2[1] / DIG_BASE)；

x = start1[0] + ((dec2)dcarry) * DIG_BASE;
y = start1[1];
guess = (norm_factor * x + norm_factor * y / DIG_BASE) / norm2;

for (carry = 0; buf2 > start2; buf1--) {
  dec1 hi, lo;
  x = guess * (*--buf2);
  hi = (dec1)(x / DIG_BASE);
  lo = (dec1)(x - ((dec2)hi) * DIG_BASE);
  SUB2(*buf1, *buf1, lo, carry);
  carry += hi;
}
carry = dcarry < carry;

3.2 ClickHouse

ClickHouse 是列存, 相同列的数据会放在一起, 因此计算时通常也将一列的数据合成 batch 一起计算.

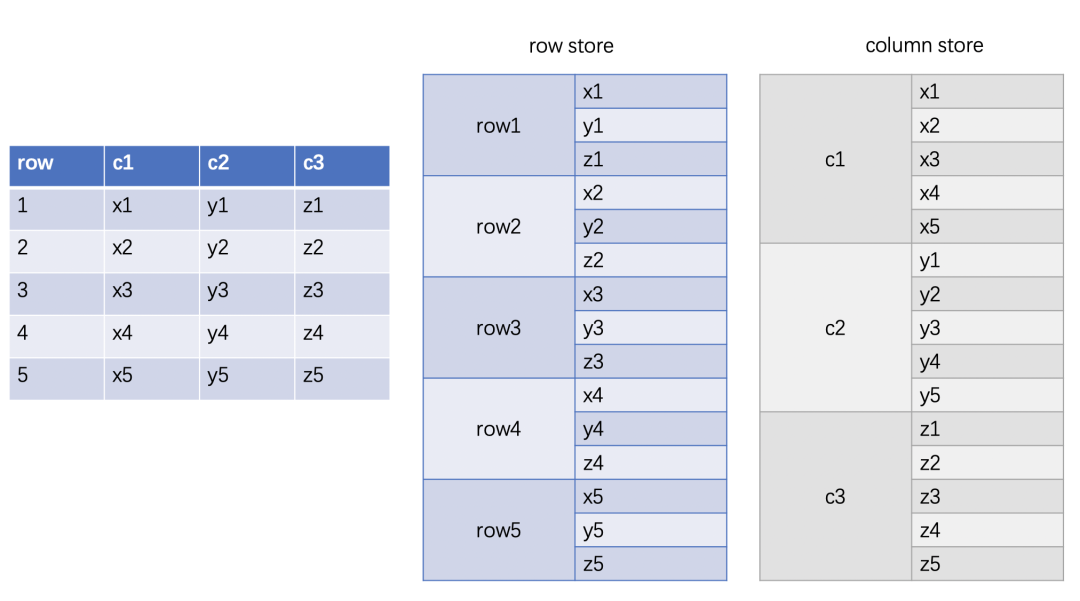
一列的 batch 在 ClickHouse 中使用 PODArray, 例如上图中的 c1 在计算时就会有一个 PODArray, 进行简化后大致可以表示如下:

class PODArray {
    char * c_start          = null;
    char * c_end            = null;
    char * c_end_of_storage = null;
}

在计算时会讲 c_start 指向的数组转换成实际的类型, 对于 decimal, ClickHouse 使用足够大的 int 来表示, 根据 decimal 的 precision 选择 int32, int64 或者 int128. 例如一个 decimal(10, 2), 123.45, 使用这样方式可以表示为一个 int32_t, 其内容为 12345, decimal(10, 3) 的 123.450 表示为 123450. ClickHouse 用来表示每个 decimal 的结构如下, 实际上就是足够大的 int：

template <typename T>
struct Decimal
{
    using NativeType = T;
    // ...
    T value;
};
using Int32 = int32_t;
using Int64 = int64_t;
using Int128 = __int128;
using Decimal32 = Decimal<Int32>;
using Decimal64 = Decimal<Int64>;
using Decimal128 = Decimal<Int128>;

显而易见, 这样的表示方法相较于 MySQL 的方法更轻量, 但是范围更小, 同时也带来了一个问题是没有小数点的位置, 在进行加减法、大小比较等需要小数点对齐的场景下, ClickHouse 会在运算实际发生的时候将 scale 以参数的形式传入, 此时配合上面的数字就可以正确地还原出真实的 decimal 值了.

ResultDataType type = decimalResultType(left, right, is_multiply, is_division);

int scale_a = type.scaleFactorFor(left, is_multiply);
int scale_b = type.scaleFactorFor(right, is_multiply || is_division);
OpImpl::vector_vector(col_left->getData(), col_right->getData(), vec_res,
                      scale_a, scale_b, check_decimal_overflow);

例如两个 decimal: a = 123.45000(p=8, s=5), b = 123.4(p=4, s=1), 那么计算时传入的参数就是 col_left->getData() = 123.45000 10 ^ 5 = 12345000, scale_a = 1, col_right->getData() = 123.4 10 ^ 1 = 1234, scale_b = 10000, 12345000 1 和 1234 10000 的小数点位置是对齐的, 可以直接计算.

加法主要步骤

ClickHouse 实现加法同样要先对齐, 对齐的方法是将 scale 较小的数字乘上一个系数, 使两边的 scale 相等. 然后直接做加法即可. ClickHouse 在计算中也根据 decimal 的 precision 进行了细分, 对于长度没那么长的 decimal, 直接用 int32, int64 等原生类型计算就可以了, 这样大大提升了速度.

bool overflow = false;
if constexpr (scale_left)
    overflow |= common::mulOverflow(a, scale, a);
else
    overflow |= common::mulOverflow(b, scale, b);

overflow |= Op::template apply<NativeResultType>(a, b, res);

template <typename T>
inline bool addOverflow(T x, T y, T & res)
{
    return __builtin_add_overflow(x, y, &res);
}

template <>
inline bool addOverflow(__int128 x, __int128 y, __int128 & res)
{
    static constexpr __int128 min_int128 = __int128(0x8000000000000000ll) << 64;
    static constexpr __int128 max_int128 = (__int128(0x7fffffffffffffffll) << 64) + 0xffffffffffffffffll;
    res = x + y;
    return (y > 0 && x > max_int128 - y) || (y < 0 && x < min_int128 - y);
}

乘法主要步骤

同 MySQL, 乘法不需要对齐, 直接按整数相乘就可以了, 比较短的 decimal 同样可以使用 int32, int64 原生类型. int128 在溢出检测时被转换成 unsigned int128 避免溢出时的未定义行为.

template <typename T>
inline bool mulOverflow(T x, T y, T & res)
{
    return __builtin_mul_overflow(x, y, &res);
}

template <>
inline bool mulOverflow(__int128 x, __int128 y, __int128 & res)
{
    res = static_cast<unsigned __int128>(x) * static_cast<unsigned __int128>(y);    /// Avoid signed integer overflow.
    if (!x || !y)
        return false;

    unsigned __int128 a = (x > 0) ? x : -x;
    unsigned __int128 b = (y > 0) ? y : -y;
    return (a * b) / b != a;
}

除法主要步骤

先转换 scale 再直接做整数除法. 本身来讲除法和乘法一样是不需要对齐小数点的, 但是除法不一样的地方在于可能会产生无限小数, 所以一般数据库都会给结果一个固定的小数位数, ClickHouse 选择的小数位数是和被除数一样, 因此需要将 a 乘上 scale, 然后在除法运算的过程中, 这个 scale 被自然减去, 得到结果的小数位数就可以保持和被除数一样.

bool overflow = false;
if constexpr (!IsDecimalNumber<A>)
    overflow |= common::mulOverflow(scale, scale, scale);
overflow |= common::mulOverflow(a, scale, a);
if (overflow)
    throw Exception("Decimal math overflow", ErrorCodes::DECIMAL_OVERFLOW);

return Op::template apply<NativeResultType>(a, b);

3.3 总结

MySQL 通过一个 int32 的数组来表示一个大数, ClickHouse 则是尽可能使用原生类型, GCC 和 Clang 都支持 int128 扩展, 这使得 ClickHouse 的这种做法可以比较方便地实现.

MySQL 与 ClickHouse 的实现差别还是比较大的, 针对我们开始提到的问题, 分别来看看他们的解答.

1. precision 和 scale 范围, MySQL 最高可定义 precision=65, scale=30, 中间结果最多包含 81 个数字, ClickHouse 最高可定义 precision=38, scale=37, 中间结果最大为 int128 的最大值 -2^127 ~ 2^127-1.

2. 在哪里存储 scale, MySQL 是行式存储, 使用火山模型逐行迭代, 计算也是按行进行, 每个 decimal 都有自己的 scale；ClickHouse 是列式存储, 计算按列批量进行, 每行按照相同的 scale 处理能提升性能, 因此 scale 来自表达式解析过程中推导出来的类型.

3. scale 增长, scale 增长超过极限时, MySQL 会通过动态挤占小数空间, truncate 运算数, 尽可能保证计算完成, ClickHouse 会直接报溢出错.

4. 除法 scale, MySQL 通过 div_prec_increment 来控制除法结果的 scale, ClickHouse 固定使用被除数的 scale.

5. 性能, MySQL 使用了更宽的 decimal 表示, 同时要进行 ROUND_UP, 小数挤占, TRUNCATE 等动作, 性能较差, ClickHouse 使用原生的数据类型和计算最大限度地提升了性能.

4. MySQL 违反直觉的地方

在这一部分中, 我们将讲述一些 MySQL 实现造成的违反直觉的地方. 这些行为通常发生在运算结果接近 81 digit 时, 因此如果可以保证运算结果的范围较小也可以忽略这些问题.

1. 乘法的 scale 会截断到 31, 且该截断是通过截断运算数字的方式来实现的, 例如: select 10000000000000000000000000000000.100000000 10000000000000000000000000000000 = 10000000000000000000000000000000.100000000000000000000000000000 10000000000000000000000000000000.555555555555555555555555555555 返回 1, 第二个运算数中的 .555555555555555555555555555555 全部被截断

2. MySQL 使用的 buffer 包含了 81 个 digit 的容量, 但是由于小数部分必须和整数部分分开, 因此很多时候无法用满 81 个 digit, 例如: select 99999999999999999999999999999999999999999999999999999999999999999999999999.999999 = 99999999999999999999999999999999999999999999999999999999999999999999999999.9 返回 1

3. 计算过程中如果发现整数部分太大会动态地挤占小数部分, 例如: select 999999999999999999999999999999999999999999999999999999999999999999999999.999999999 + 999999999999999999999999999999999999999999999999999999999999999999999999.999999999 = 999999999999999999999999999999999999999999999999999999999999999999999999 + 999999999999999999999999999999999999999999999999999999999999999999999999 返回 1

4. 除法计算中间结果不受 scale = 31 的限制, 除法中间结果的 scale 一定是 9 的整数倍, 不能按照最终结果来推测除法作为中间结果的精度, 例如 select 2.0000 / 3 3 返回 2.00000000, 而 select 2.00000 / 3 3 返回 1.999999998, 可见前者除法的中间结果其实保留了更多的精度.

5. 除法, avg 计算最终结果的小数部分如果正好是 9 的倍数, 则不会四舍五入, 例如: select 2.00000 / 3 返回 0.666666666, select 2.0000 / 3 返回 0.66666667

6. 除法, avg 计算时, 运算数字的小数部分如果不是 9 的倍数, 那么会实际上存储 9 的倍数个小数数字, 因此会出现以下差异：

create table t1 (a decimal(20, 2), b decimal(20, 2), c integer);

insert into t1 values (100000.20, 1000000.10,   5);
insert into t1 values (200000.20, 2000000.10,   2);
insert into t1 values (300000.20, 3000000.10,   4);
insert into t1 values (400000.20, 4000000.10,   6);
insert into t1 values (500000.20, 5000000.10,   8);
insert into t1 values (600000.20, 6000000.10,   9);
insert into t1 values (700000.20, 7000000.10,   8);
insert into t1 values (800000.20, 8000000.10,   7);
insert into t1 values (900000.20, 9000000.10,   7);
insert into t1 values (1000000.20, 10000000.10, 2);
insert into t1 values (2000000.20, 20000000.10, 5);
insert into t1 values (3000000.20, 30000000.10, 2);

select sum(a+b), avg(c), sum(a+b) / avg(c) from t1;
+--------------+--------+-------------------+
| sum(a+b)     | avg(c) | sum(a+b) / avg(c) |
+--------------+--------+-------------------+
| 115500003.60 | 5.4167 |   21323077.590317 |
+--------------+--------+-------------------+
1 row in set (0.01 sec)

select 115500003.60 / 5.4167;
+-----------------------+
| 115500003.60 / 5.4167 |
+-----------------------+
|       21322946.369561 |
+-----------------------+
1 row in set (0.00 sec)

위 내용은 mysql 데이터베이스에서 Decimal 유형을 사용하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!