MySql 인덱스를 만드는 방법

1. B+ 트리 인덱스

이름에서 알 수 있듯이 B+ 트리 구조의 인덱스는 일반적인 상황에서 InnoDb 엔진에서 생성되는 일반 인덱스는 B+ 구조를 갖습니다.

B+ 트리 인덱스는 다음과 같습니다.

1.1. 클러스터형 인덱스/클러스터형 인덱스

기본 키를 정의할 때 기본 키에 자동으로 추가되는 인덱스는 클러스터형 인덱스라고도 합니다.

Mysql에서는 구성요소를 사용하여 B+ 트리 구조를 구성합니다. 그림에 표시된 것처럼 각 리프 노드는 기본 키 및 기타 관련 데이터에 해당합니다.

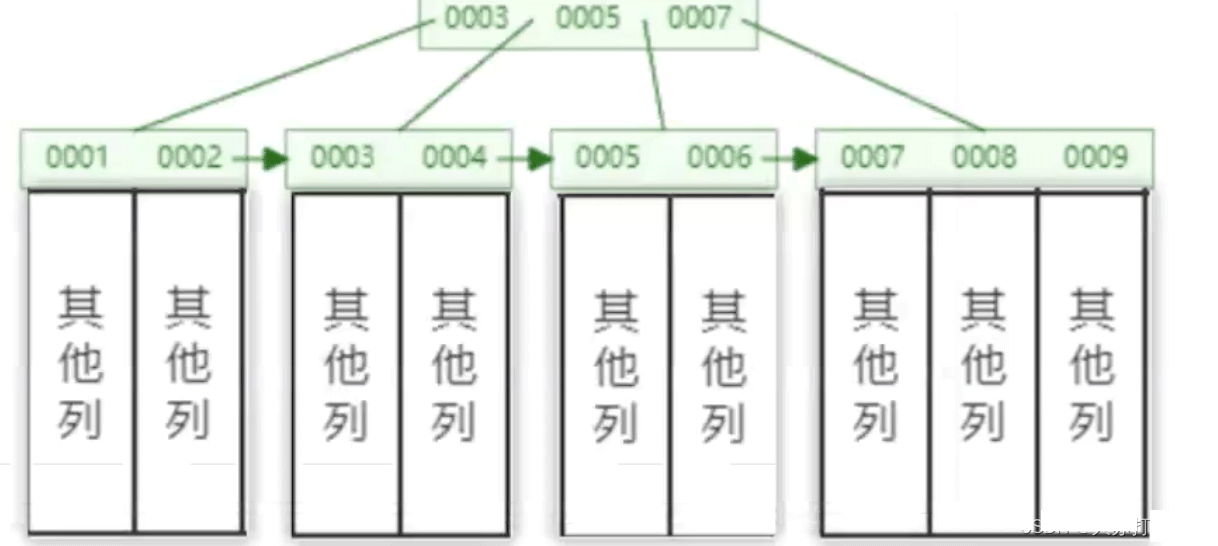
테이블 생성 시 기본 키를 정의하지 않으면 MySQL은 자동으로 기본 키와 해당 인덱스를 생성합니다. 기본 키 이름은 rowIdrowId

1.2、辅助索引/二级索引

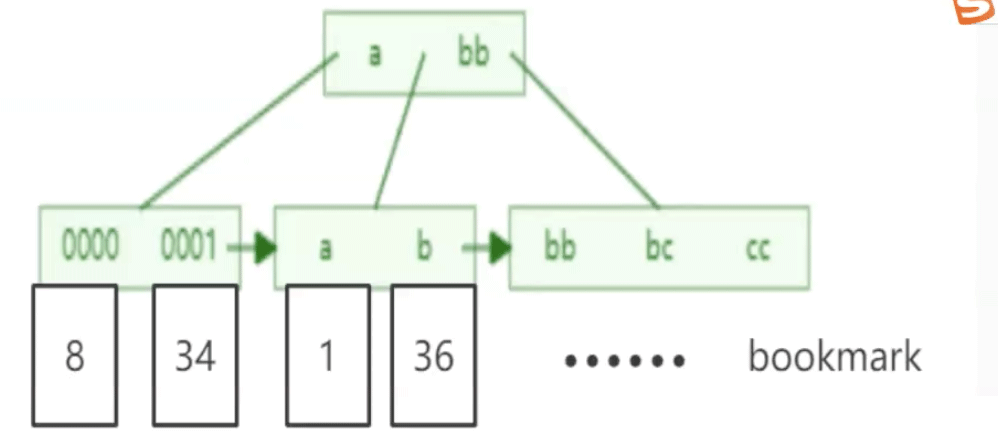
辅助索引，也称为二级索引，是指对于非主键列column创建的索引。同样的，Mysql会为这个索引创建一个B+树，树的叶子节点除了包含这个列column的值以外，就只包含这个列所在行的主键值，这样通过列的索引就可以查到叶子节点，然后叶子节点中的主键信息再从主键的索引中搜索，最终得到一整行的数据。

通过二级索引找到主键，再从主键得到一整行数据的行为叫做回表。

1.3、联合索引/复合索引

1.3.1、什么是复合索引

聚合索引可以说是二级索引的一种特殊情况。一般二级索引都是只对一个非主键的列添加索引，而聚合索引则是一次性对多个列同时添加索引。

一般的二级索引用这样的语句创建：

CREATE INDEX  order_name_index on t_order(order_name);

复合索引则是这样创建：

CREATE INDEX  order_name_and_order_type_index on t_order(order_name, order_type);

对于复合索引，Mysql会也会创建一个B+树，但因为是多个列的索引，所以B+树的排序规则比较特殊，是遵循最左原则。下面会讲到什么是最左原则。

之后叶子节点包含的信息有多个，一个是作为索引的各个列的值，另一个就是主键的值。

1.3.2、最左原则

所谓的最左原则是，B+树的排序规则是根据索引定义时，定义的语句中的列名从左到右进行排序。

比如定义语句如下：

CREATE INDEX  joint_index on t_order(order_name, order_type, submit_time);

那排序规则是先排order_name，如果order_name相同，再排order_type，最后排submit_time。

那当我们查询时，根据定义时列的顺序从左至右，where子句或者order by等子句应该尽量先从order_name开始，然后以此类推。

比如说，我们已经定义了上面的三个列组成的复合索引，那查询或者排序的时候尽量先order_name，再order_type，最后submit_time。

select * from t_order where order_name = 'order1'
and order_type = 1
and submit_time = str_to_date('2022-08-02 00:52:26', '%Y-%m-%d %T')

原因很简单，因为联合索引的排序规则是先排order_name，如果order_name相同，再排order_type，最后排submit_time。所以只有查询排序时也遵循这个规则，我们才能用上索引。

如果我们不完全遵守最左原则，比如查询排序只排两个列，忽略中间那个order by order_name, submit_time。那这个时候Mysql会有智能化的处理，他会自己判断是用索引快还是不用索引快。

1.3.3、联合索引的查询优化

尽量使用到组成联合索引的列，并且保证顺序。可以通过查询索引查看列的顺序。查看sql_in_index

show index from t_order;

查询返回的字段尽量就只返回组成联合索引的列和主键，不要返回其它的列，以免造成回表。
这应该容易理解，因为联合索引的B+树的叶子节点就只包含主键和组成联合索引的列的值，如果返回的字段就这几列，那在一个B+树种查询就完事了。如果还要返回其它的列的话，就又要去主键的索引中查找，有回表操作。

2、哈希索引

一般数据库都会用B+树索引查询数据，但是当数据库使用一段时间后，InnoDB 会记录一些使用频率较高的热数据，然后为这些热数据建立哈希结构的索引，这就是哈希索引的应用场景。

这个索引在Mysql 5.7开始默认开启。

2.1、查看哈希索引的命中率等信息

使用语句：

show engine innodb status;

其中的status

1.2, 보조 인덱스/보조입니다. index🎜🎜보조 인덱스라고도 하는 보조 인덱스는 기본 키가 아닌 열에 대해 생성된 인덱스를 참조합니다. 마찬가지로 Mysql은 이 인덱스에 대한 B+ 트리를 생성하며, 트리의 리프 노드에는 해당 열이 위치한 행의 기본 키 값만 포함됩니다. 그런 다음 기본 키 인덱스에서 리프 노드의 기본 키 정보를 검색하고 마지막으로 전체 행의 데이터를 얻습니다. 🎜🎜보조 인덱스를 통해 기본 키를 찾은 다음 기본 키에서 전체 행의 데이터를 가져오는 행위를 테이블 반환이라고 합니다. 🎜🎜🎜🎜1.3, 조인트 인덱스/ 복합지수 🎜

1.3.1. 복합지수란 무엇인가요?

🎜집계지수는 보조지수의 특별한 경우라고 할 수 있습니다. 일반적으로 보조 인덱스는 기본 키가 아닌 하나의 열에만 인덱스를 추가하는 반면, 집계 인덱스는 한 번에 여러 열에 인덱스를 추가합니다. 🎜🎜일반 보조 인덱스는 다음 명령문으로 생성됩니다:🎜

-------------------------------------
INSERT BUFFER AND ADAPTIVE HASH INDEX
-------------------------------------
Ibuf: size 1, free list len 0, seg size 2, 0 merges
merged operations:
 insert 0, delete mark 0, delete 0
discarded operations:
 insert 0, delete mark 0, delete 0
Hash table size 34679, node heap has 0 buffer(s)
Hash table size 34679, node heap has 0 buffer(s)
Hash table size 34679, node heap has 5 buffer(s)
Hash table size 34679, node heap has 0 buffer(s)
Hash table size 34679, node heap has 1 buffer(s)
Hash table size 34679, node heap has 0 buffer(s)
Hash table size 34679, node heap has 1 buffer(s)
Hash table size 34679, node heap has 1 buffer(s)
-- 哈希索引的命中率，可根据这个来决定是否使用哈希索引
0.00 hash searches/s, 0.00 non-hash searches/s
---

🎜복합 인덱스는 다음과 같이 생성됩니다:🎜

select count(distinct id)/count(*) form t_table;

🎜복합 인덱스의 경우 Mysql도 하나를 생성합니다. B+ 트리이지만 여러 열의 인덱스이기 때문에 B+ 트리의 정렬 규칙은 매우 특별하며 가장 왼쪽 원칙을 따릅니다. 가장 왼쪽의 원칙은 무엇인지 아래에서 논의하겠습니다. 🎜🎜이후 리프 노드에는 여러 정보가 포함됩니다. 하나는 인덱스로 사용되는 각 열의 값이고, 다른 하나는 기본 키의 값입니다. 🎜

1.3.2. 최좌측 원칙

🎜 소위 B+ 트리의 정렬 규칙은 인덱스가 정의될 ​​때 정의된 문의 열 이름을 왼쪽에서 오른쪽으로 정렬하는 것입니다. . 🎜🎜예를 들어 정의문이 다음과 같은 경우: 🎜

SELECT COUNT(DISTINCT LEFT(order_note,3))/COUNT(*) AS sel3,
COUNT(DISTINCT LEFT(order_note,4))/COUNT(*)AS sel4,
COUNT(DISTINCT LEFT(order_note,5))/COUNT(*) AS sel5,
COUNT(DISTINCT LEFT(order_note, 6))/COUNT(*) As sel6,
COUNT(DISTINCT LEFT(order_note, 7))/COUNT(*) As sel7,
COUNT(DISTINCT LEFT(order_note, 8))/COUNT(*) As sel8,
COUNT(DISTINCT LEFT(order_note, 9))/COUNT(*) As sel9,
COUNT(DISTINCT LEFT(order_note, 10))/COUNT(*) As sel10,
COUNT(DISTINCT LEFT(order_note, 11))/COUNT(*) As sel11,
COUNT(DISTINCT LEFT(order_note, 12))/COUNT(*) As sel12,
COUNT(DISTINCT LEFT(order_note, 13))/COUNT(*) As sel13,
COUNT(DISTINCT LEFT(order_note, 14))/COUNT(*) As sel14,
COUNT(DISTINCT LEFT(order_note, 15))/COUNT(*) As sel15,
COUNT(DISTINCT order_note)/COUNT(*) As total
FROM order_exp;

🎜정렬 규칙은 order_name을 먼저 정렬하는 것이고, order_name이 동일하고 order_type< /code>을 정렬하면 마지막 행은 <code>submit_time입니다. 🎜🎜그런 다음 쿼리할 때 정의에 따라 왼쪽에서 오른쪽으로 열의 순서에 따라 where 절 또는 order by 및 기타 절이 시작되도록 시도해야 합니다. order_name Start 등으로. 🎜🎜예를 들어, 위의 세 열로 구성된 복합 인덱스를 정의했습니다. 쿼리하거나 정렬할 때 먼저 order_name을 시도한 다음 order_type을 시도하고 마지막으로 를 시도합니다. submit_time. 🎜

alter table order_exp add key(order_note(13));

🎜이유는 매우 간단합니다. 왜냐하면 공동 색인의 정렬 규칙은 order_name을 먼저 정렬하고 order_name이 동일하면 order_type<을 정렬하는 것이기 때문입니다. /code>, 마지막으로 < code>submit_time입니다. 따라서 쿼리 정렬 시 이 규칙을 준수해야만 인덱스를 사용할 수 있습니다. 🎜🎜예를 들어, 가장 왼쪽 원칙을 완전히 준수하지 않으면 쿼리 정렬은 가운데 order by order_name, submit_time을 무시하고 두 개의 열만 정렬합니다. 이때 Mysql은 지능적인 처리 기능을 갖게 되며 인덱스를 사용하는 것이 더 빠른지 여부를 판단하게 됩니다. 🎜

1.3.3.결합 인덱스 쿼리 최적화

🎜 결합 인덱스를 구성하는 열을 사용하고 순서를 보장해 보세요. 컬럼의 순서는 인덱스를 쿼리하여 확인할 수 있습니다. sql_in_index🎜

CREATE TABLE customer (
	cno INT,
	lname VARCHAR (10),
	fname VARCHAR (10),
	sex INT,
	weight INT,
	city VARCHAR (10)
);

CREATE INDEX idx_cust ON customer (city, lname, fname, cno);

🎜🎜🎜쿼리가 반환됨 보기 fields 공동 인덱스를 구성하는 열과 기본 키만 반환하고 테이블 백업을 피하기 위해 다른 열은 반환하지 마십시오.
조인 인덱스의 B+ 트리의 리프 노드에는 기본 키와 조인트 인덱스를 구성하는 열의 값만 포함되므로 이해하기 쉽습니다. 열이면 B+ 트리의 쿼리가 완료됩니다. 다른 컬럼을 반환하려면 기본키의 인덱스를 검색하여 테이블 반환 작업을 수행해야 합니다. 🎜🎜2. 해시 인덱스🎜🎜일반 데이터베이스는 B+ 트리 인덱스를 사용하여 데이터를 쿼리하지만, 데이터베이스를 일정 기간 동안 사용하면 InnoDB는 더 자주 사용되는 일부 핫 데이터를 기록한 다음 이에 대한 해시 구조 인덱스를 생성합니다. 이러한 핫 데이터는 해시 인덱스의 적용 시나리오입니다. 🎜🎜이 인덱스는 Mysql 5.7부터 기본적으로 활성화되어 있습니다. 🎜🎜2.1. 해시 인덱스의 적중률 및 기타 정보를 확인하세요. 🎜🎜사용 설명: 🎜

select cno,fname from customer where lname='xx' and city ='yy' order by fname;

🎜🎜🎜상태에는 해시 인덱스를 비롯한 많은 정보가 포함되어 있습니다. 정보를 편집기에 복사하여 봅니다. 이 섹션은 해시 인덱스 정보입니다. 🎜

-------------------------------------
INSERT BUFFER AND ADAPTIVE HASH INDEX
-------------------------------------
Ibuf: size 1, free list len 0, seg size 2, 0 merges
merged operations:
 insert 0, delete mark 0, delete 0
discarded operations:
 insert 0, delete mark 0, delete 0
Hash table size 34679, node heap has 0 buffer(s)
Hash table size 34679, node heap has 0 buffer(s)
Hash table size 34679, node heap has 5 buffer(s)
Hash table size 34679, node heap has 0 buffer(s)
Hash table size 34679, node heap has 1 buffer(s)
Hash table size 34679, node heap has 0 buffer(s)
Hash table size 34679, node heap has 1 buffer(s)
Hash table size 34679, node heap has 1 buffer(s)
-- 哈希索引的命中率，可根据这个来决定是否使用哈希索引
0.00 hash searches/s, 0.00 non-hash searches/s
---

3、索引的创建策略

3.1、 单列索引的策略

3.1.1、列的类型占用的空间越小，越适合作为索引

因为B+树也是占用空间的，所以在固定空间中，如果列的类型占用的空间越小，那我们一次就能读取更多的B+树节点，这样自然就加快了效率。

3.1.2、根据列的值的离散性

离散性是指数据的值重复的程度高不高，假如有N条数据的话，那离散性就可以用数值表示，范围是1/N 到 1。

比如说某个列在数据库中有下面几条数据（1, 2, 3, 4, 5, 5, 3），其中5和3都有重复，去重后应该是（1, 2, 3, 4, 5）。我们将去重后的条数除以总条数就得到离散性。这里是5/7。列中重复数据较多时，对应的数值较小，而重复数据较少时，数值相应较大。

如果一个列的数据的重复性越低，那么这个列就越适合加索引。

因为索引是需要起到筛选的作用。比如我们有个where条件是where id = 1，如果数据重复性较高，那可能根据索引会返回100条数据，然后我们在根据其他where条件在100条数据中再筛选。

如果数据重复性较低，那可能就只返回1条数据，那之后的运算量明显小得多。

所以一个列的数据离散性越高，那这个列越适合添加索引。

我们可以用下面的语句得到某个列的离散性程度。

select count(distinct id)/count(*) form t_table;

3.1.3、前缀索引

前缀索引和后缀索引：

有些列的值比较长，比如一些备注日志信息也会记录在数据库当中，这类信息的长度往往比较长，如果我们需要对这类列加索引，那索引并不是索引字符串的全部长度。这时候我们就可以建立前缀索引，即对字符串的前面几位建立索引。

所以前缀索引就是建立范围更小索引，选择一个好前缀位数就能有一个更好的查询效率。

不过有一些缺点，就是这类索引无法应用到order by和group语句上。

Mysql没有后缀索引，如果非要实现后缀索引，那在数据存储时我们应该将数据反转，这样就能用前缀索引达到后缀索引的效果。后缀索引的一个经典应用就是邮箱，快速查询某种类型的邮箱。

选择前缀索引的位数：

这里的逻辑和列的离散性类似，我们需要看看字符串的前面几位的子字符串的离散性如何。比如对于下面的表，内容是电影票的相关信息，我们需要对order_note建立前缀索引。

来比较一下各个位的子字符串的离散性。

SELECT COUNT(DISTINCT LEFT(order_note,3))/COUNT(*) AS sel3,
COUNT(DISTINCT LEFT(order_note,4))/COUNT(*)AS sel4,
COUNT(DISTINCT LEFT(order_note,5))/COUNT(*) AS sel5,
COUNT(DISTINCT LEFT(order_note, 6))/COUNT(*) As sel6,
COUNT(DISTINCT LEFT(order_note, 7))/COUNT(*) As sel7,
COUNT(DISTINCT LEFT(order_note, 8))/COUNT(*) As sel8,
COUNT(DISTINCT LEFT(order_note, 9))/COUNT(*) As sel9,
COUNT(DISTINCT LEFT(order_note, 10))/COUNT(*) As sel10,
COUNT(DISTINCT LEFT(order_note, 11))/COUNT(*) As sel11,
COUNT(DISTINCT LEFT(order_note, 12))/COUNT(*) As sel12,
COUNT(DISTINCT LEFT(order_note, 13))/COUNT(*) As sel13,
COUNT(DISTINCT LEFT(order_note, 14))/COUNT(*) As sel14,
COUNT(DISTINCT LEFT(order_note, 15))/COUNT(*) As sel15,
COUNT(DISTINCT order_note)/COUNT(*) As total
FROM order_exp;

可以看出，前面几位的子字符串的离散程度较低，后面sel13开始就比较高，那我们可以根据实际情况，建立13~15位的前缀索引。

建立前缀索引SQL语句：

alter table order_exp add key(order_note(13));

3.1.2、只为搜索、排序和分组的列建索引

这个理由很简单，不解释了。

3.2、 多列索引的策略

3.2.1、离散性最高的列放前面

原因很简单，查询时根据定义复合索引时的列的顺序来查询的，离散性高的列放在前面的话，就能更早的将更多的数据排除在外。

3.2.2、三星索引

三星索引是一种策略。有三种条件，满足一条则索引获得一颗星，三颗星则是很好的索引。

三条策略分别是

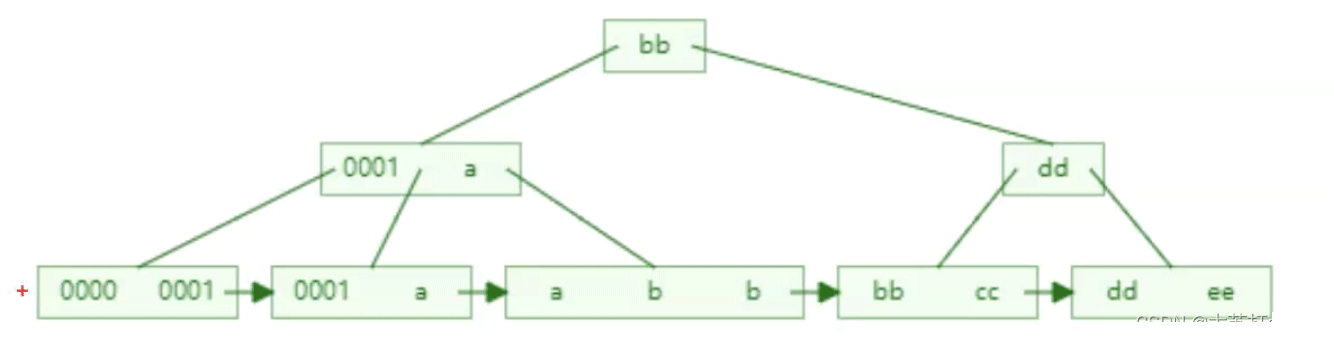
索引将相关记录放在一起。

意思是查询需要的数据在索引树的叶子节点中连续或者足够靠近。举个例子，下面是某个索引的B+树。查询所需数据仅在叶节点的前两个范围内，即0000至a。这很明显，后面的片我们就没必要再去查询了，这无疑增加了效率。当所需数据分布在每个片上时，查询次数就会显著增加。

所以查询需要的数据在叶子节点上越连续，越窄就越好。

索引中的数据顺序与查找中的数据排序一致。

这容易理解，讲解联合索引中说过，B+树的排序顺序和索引中的数据一样，所以查询时的where的数据顺序越贴近索引中的顺序，就越能更好地利用B+树。

索引的列包含查询中的所有列。

这个可以避免回文操作，不多解释。

三星索引的权重：

一般来说第三个策略权重占到50%，之后是第一个策略27%， 第二个策略23%。

三星索引实例：

CREATE TABLE customer (
	cno INT,
	lname VARCHAR (10),
	fname VARCHAR (10),
	sex INT,
	weight INT,
	city VARCHAR (10)
);

CREATE INDEX idx_cust ON customer (city, lname, fname, cno);

我们创建以上的索引，那么对于下面的查询语句，这个索引就是三星索引。

select cno,fname from customer where lname='xx' and city ='yy' order by fname;

首先，查询条件中有lname=’xx’ and city =’yy’，这条件让我们这需要在lname=’xx’ and city =’yy’的那一片B+树的叶子节点中查询，让我们的查询变窄了很多，并且这部分的数据是连续的，因为B+树是先根据city排序，再根据lname查询。

另外，因为已经锁定lname=’xx’ and city =’yy’，所以这部分的数据是根据fname和cno排序。查询语句正好是根据`fname```排序，所以第二点也满足。

最后是查询的结果都包含正在索引中，不会有回文，第三点也满足，所以这个索引是三星索引。

위 내용은 MySql 인덱스를 만드는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!