신경기호 프로그래밍의 힘을 보여주다
지난 몇 년 동안 우리는 Transformer 기반 모델이 등장하고 자연어 처리나 컴퓨터 비전 등 다양한 분야에서 성과를 거두었습니다. . 성공적인 신청. 이 글에서는 딥 러닝 모델, 특히 Transformer를 하이브리드 아키텍처로 표현하는 간결하고 해석 가능하며 확장 가능한 방법, 즉 딥 러닝과 상징적 인공 지능을 결합하는 방법을 살펴보겠습니다. 따라서 우리는 PyNeuraLogic이라는 Python 신경 기호 프레임워크에서 모델을 구현할 것입니다.
심볼 표현과 딥 러닝을 결합하여 기본 해석 가능성 및 누락된 추론 기술과 같은 현재 딥 러닝 모델의 공백을 메웁니다. 아마도 카메라의 메가픽셀 수를 늘리는 것이 반드시 더 나은 사진을 생성하는 것은 아닌 것처럼 매개변수 수를 늘리는 것이 원하는 결과를 얻는 가장 합리적인 방법은 아닐 것입니다.
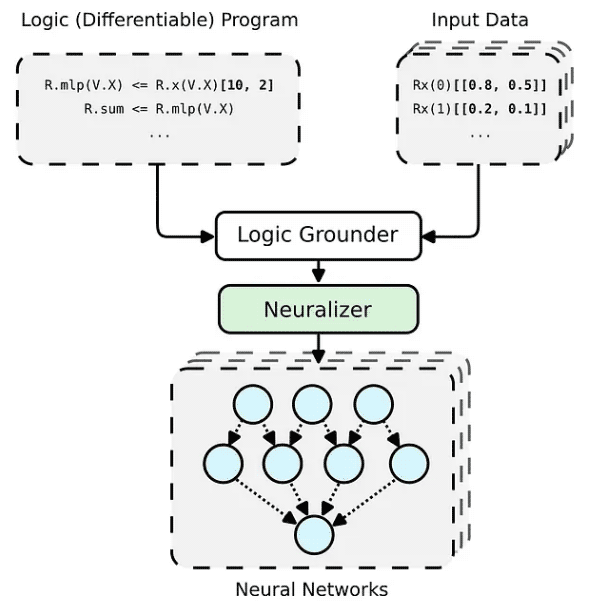
PyNeuraLogic 프레임워크는 논리 프로그래밍을 기반으로 합니다. 논리 프로그램에는 미분 가능한 매개변수가 포함되어 있습니다. 이 프레임워크는 더 작은 구조의 데이터(예: 분자)와 복잡한 모델(예: 변환기 및 그래프 신경망)에 매우 적합합니다. PyNeuraLogic은 비관계형 및 대규모 텐서 데이터에 대한 최선의 선택이 아닙니다.
프레임워크의 핵심 구성 요소는 템플릿이라고 부르는 미분 가능한 논리 프로그램입니다. 템플릿은 추상적인 방식으로 신경망의 구조를 정의하는 논리적 규칙으로 구성됩니다. 템플릿을 모델 아키텍처의 청사진으로 생각할 수 있습니다. 그런 다음 템플릿은 각 입력 데이터 인스턴스에 적용되어 (기본 및 신경화를 통해) 입력 샘플에 고유한 신경망을 생성합니다. 사전 정의된 다른 아키텍처와 완전히 다른 이 프로세스는 다른 입력 샘플에 맞게 자체 조정될 수 없습니다.
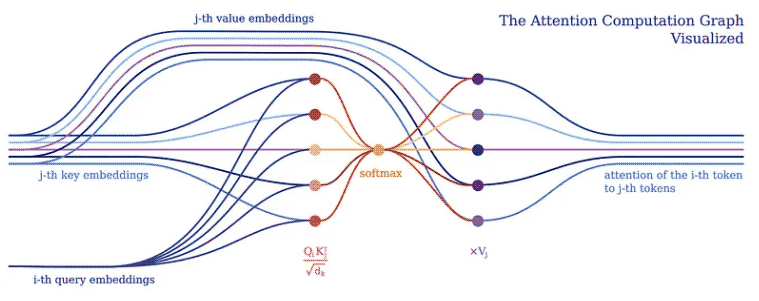
일반적으로 우리는 입력 토큰 일괄 처리에 대해 대규모 텐서 연산을 수행하는 딥 러닝 모델을 구현합니다. 이는 딥 러닝 프레임워크와 하드웨어(예: GPU)가 일반적으로 다양한 모양과 크기의 여러 텐서가 아닌 더 큰 텐서를 처리하는 데 최적화되어 있기 때문에 의미가 있습니다. 변환기도 예외는 아니며 일반적으로 단일 토큰 벡터 표현을 큰 행렬로 일괄 처리하고 모델을 그러한 행렬에 대한 작업으로 나타냅니다. 그러나 이러한 구현은 Transformer의 주의 메커니즘에서 알 수 있듯이 개별 입력 토큰이 서로 어떻게 관련되어 있는지 숨깁니다.
어텐션 메커니즘은 모든 Transformer 모델의 핵심을 형성합니다. 특히 클래식 버전은 다중 헤드 스케일링 도트 제품 주의를 사용합니다. 명확성을 위해 헤더를 사용하여 스케일링된 내적 주의를 간단한 논리 프로그램으로 분해해 보겠습니다.
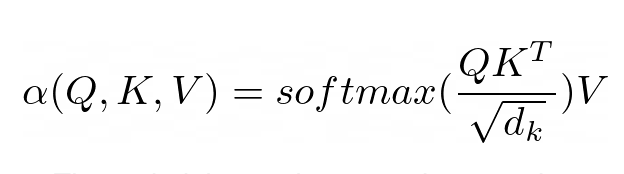
주의의 목적은 네트워크가 집중해야 하는 입력 부분을 결정하는 것입니다. 구현 시 가중치 계산값 V에 주의해야 한다. 가중치는 입력 키 K와 쿼리 Q의 호환성을 나타낸다. 이 특정 버전에서 가중치는 쿼리 Q와 쿼리 키 K의 내적을 입력 특징 벡터 차원 d_k의 제곱근으로 나눈 소프트맥스 함수로 계산됩니다.
(R.weights(V.I, V.J) <= (R.d_k, R.k(V.J).T, R.q(V.I))) | [F.product, F.softmax_agg(agg_terms=[V.J])], (R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.J)) | [F.product]
PyNeuraLogic에서는 위의 논리 규칙을 통해 Attention 메커니즘을 완전히 포착할 수 있습니다. 첫 번째 규칙은 가중치 계산을 나타냅니다. 이는 차원의 역제곱근과 전치된 j번째 키 벡터 및 i번째 쿼리 벡터의 곱을 계산합니다. 다음으로, 소프트맥스 함수를 사용하여 i의 결과를 가능한 모든 j로 집계합니다.
두 번째 규칙은 이 가중치 벡터와 해당 j번째 값 벡터 사이의 곱을 계산하고 각 i번째 토큰에 대해 서로 다른 j에 대한 결과를 합산합니다.
교육 및 평가 중에 입력 토큰이 참여할 수 있는 항목을 제한하는 경우가 많습니다. 예를 들어, 마커를 제한하여 앞을 내다보고 다가오는 단어에 집중하려고 합니다. PyTorch와 같은 널리 사용되는 프레임워크는 마스킹을 통해 이를 달성합니다. 즉, 스케일링된 내적 결과의 요소 하위 집합을 매우 낮은 음수로 설정합니다. 이 숫자는 소프트맥스 함수가 해당 태그 쌍의 가중치를 0으로 설정하도록 지정합니다.
(R.weights(V.I, V.J) <= (
R.d_k, R.k(V.J).T, R.q(V.I), R.special.leq(V.J, V.I)
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],기호에 신체 관계 제약 조건을 추가하면 이를 쉽게 달성할 수 있습니다. 가중치를 계산하기 위해 i번째 지표가 j번째 지표보다 크거나 같도록 제한합니다. 마스크와 달리 우리는 필요한 스케일링된 내적만을 계산합니다.
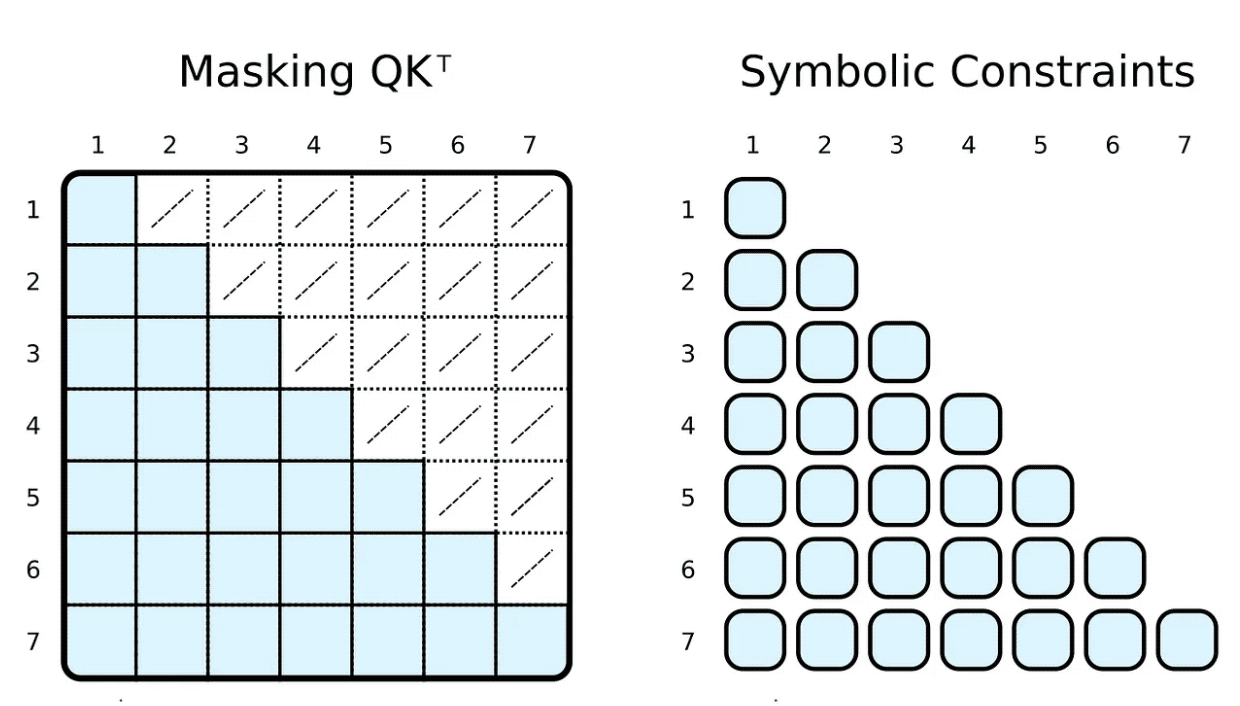
물론 상징적인 "마스킹"은 완전히 임의적일 수 있습니다. 대부분의 사람들은 희소 변환기 기반 GPT-3⁴ 또는 ChatGPT와 같은 애플리케이션에 대해 들어봤습니다. ⁵ 스파스 트랜스포머 어텐션(스트라이드 버전)에는 두 가지 유형의 어텐션 헤드가 있습니다.
一个只关注前 n 个标记 (0 ≤ i − j ≤ n)
一个只关注每第 n 个前一个标记 ((i − j) % n = 0)
两种类型的头的实现都只需要微小的改变(例如,对于 n = 5)。
(R.weights(V.I, V.J) <= (
R.d_k, R.k(V.J).T, R.q(V.I),
R.special.leq(V.D, 5), R.special.sub(V.I, V.J, V.D),
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],(R.weights(V.I, V.J) <= (
R.d_k, R.k(V.J).T, R.q(V.I),
R.special.mod(V.D, 5, 0), R.special.sub(V.I, V.J, V.D),
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],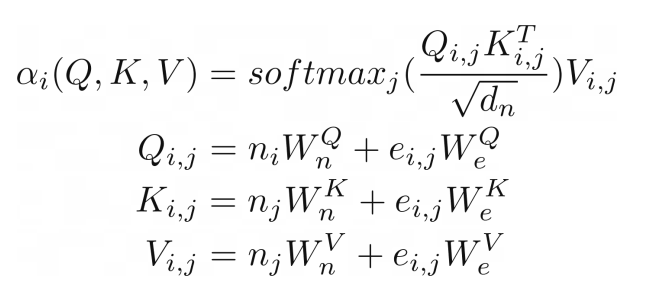
我们可以进一步推进,将类似图形输入的注意力概括到关系注意力的程度。⁶ 这种类型的注意力在图形上运行,其中节点只关注它们的邻居(由边连接的节点)。结果是节点向量嵌入和边嵌入的键 K、查询 Q 和值 V 相加。
(R.weights(V.I, V.J) <= (R.d_k, R.k(V.I, V.J).T, R.q(V.I, V.J))) | [F.product, F.softmax_agg(agg_terms=[V.J])], (R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.I, V.J)) | [F.product], R.q(V.I, V.J) <= (R.n(V.I)[W_qn], R.e(V.I, V.J)[W_qe]), R.k(V.I, V.J) <= (R.n(V.J)[W_kn], R.e(V.I, V.J)[W_ke]), R.v(V.I, V.J) <= (R.n(V.J)[W_vn], R.e(V.I, V.J)[W_ve]),
在我们的示例中,这种类型的注意力与之前展示的点积缩放注意力几乎相同。唯一的区别是添加了额外的术语来捕获边缘。将图作为注意力机制的输入似乎很自然,这并不奇怪,因为 Transformer 是一种图神经网络,作用于完全连接的图(未应用掩码时)。在传统的张量表示中,这并不是那么明显。
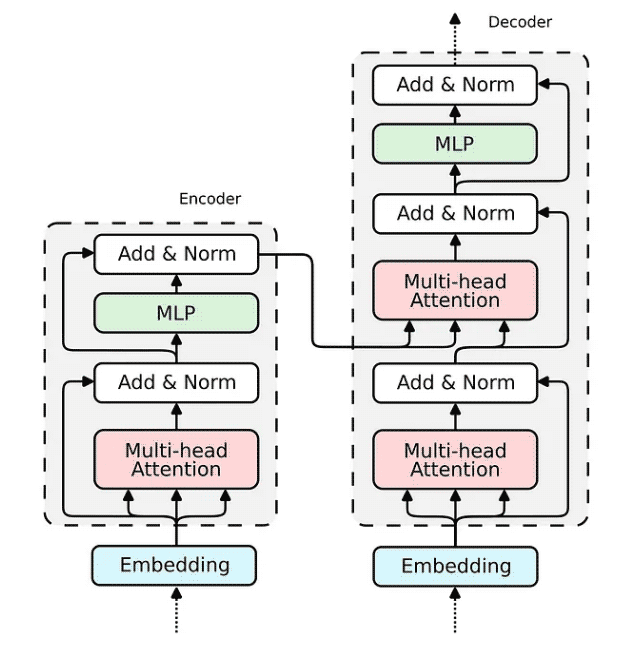
现在,当我们展示 Attention 机制的实现时,构建整个 transformer 编码器块的缺失部分相对简单。
如何在 Relational Attention 中实现嵌入已经为我们所展现。对于传统的 Transformer,嵌入将非常相似。我们将输入向量投影到三个嵌入向量中——键、查询和值。
R.q(V.I) <= R.input(V.I)[W_q], R.k(V.I) <= R.input(V.I)[W_k], R.v(V.I) <= R.input(V.I)[W_v],
查询嵌入通过跳过连接与注意力的输出相加。然后将生成的向量归一化并传递到多层感知器 (MLP)。
(R.norm1(V.I) <= (R.attention(V.I), R.q(V.I))) | [F.norm],
对于 MLP,我们将实现一个具有两个隐藏层的全连接神经网络,它可以优雅地表达为一个逻辑规则。
(R.mlp(V.I)[W_2] <= (R.norm(V.I)[W_1])) | [F.relu],
最后一个带有规范化的跳过连接与前一个相同。
(R.norm2(V.I) <= (R.mlp(V.I), R.norm1(V.I))) | [F.norm],
所有构建 Transformer 编码器所需的组件都已经被构建完成。解码器使用相同的组件;因此,其实施将是类似的。让我们将所有块组合成一个可微分逻辑程序,该程序可以嵌入到 Python 脚本中并使用 PyNeuraLogic 编译到神经网络中。
R.q(V.I) <= R.input(V.I)[W_q], R.k(V.I) <= R.input(V.I)[W_k], R.v(V.I) <= R.input(V.I)[W_v], R.d_k[1 / math.sqrt(embed_dim)], (R.weights(V.I, V.J) <= (R.d_k, R.k(V.J).T, R.q(V.I))) | [F.product, F.softmax_agg(agg_terms=[V.J])], (R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.J)) | [F.product], (R.norm1(V.I) <= (R.attention(V.I), R.q(V.I))) | [F.norm], (R.mlp(V.I)[W_2] <= (R.norm(V.I)[W_1])) | [F.relu], (R.norm2(V.I) <= (R.mlp(V.I), R.norm1(V.I))) | [F.norm],
위 내용은 Python 아키텍처 PyNeuraLogic 소스 코드 분석의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!