행렬 확률 문제인가요?

여기서 행렬 확률 문제를 살펴보겠습니다. 직사각형 행렬이 있습니다. 현재 셀에서 동일한 확률로 네 방향으로 이동할 수 있습니다. 네 방향은 왼쪽, 오른쪽, 위, 아래입니다. 우리는 M[i,j] 위치에서 시작하여 N번 이동한 후의 확률을 계산하려고 합니다.
여기서 DFS 관련 작업을 해보겠습니다. 우리는 현재 방에서 시작하여 가능한 4개의 방을 재귀적으로 탐색할 것입니다. 그런 다음 한 단계 덜 걸릴 확률을 계산합니다. 네 방향의 확률은 동일하므로 각 방향은 전체 확률의 0.25를 차지합니다. 행렬 경계를 넘으면 0을 반환하고 N개의 이동이 완료되면 1을 반환합니다. 이 아이디어를 얻기 위해 알고리즘을 살펴보겠습니다.
알고리즘
matProb(m, n, x, y, N)
Begin if x,y is not in matrix boundary m, n, then return 0 if N is 0 , then return 1 prob := 0 prob := prob + matProb(m, n, x-1, y, N-1) * 0.25 prob := prob + matProb(m, n, x+1, y, N-1) * 0.25 prob := prob + matProb(m, n, x, y+1, N-1) * 0.25 prob := prob + matProb(m, n, x, y-1, N-1) * 0.25 return prob End
예
#include<iostream>
using namespace std;
bool isSafe(int x, int y, int m, int n) { //function to check whether (x,y)
is in matrix or not
if(x >= 0 && x < m && y >= 0 && y < n){
return true;
}
return false;
}
double matProb(int m, int n, int x, int y, int N) {
if (!isSafe(x, y, m, n)) //if coundary is crossed
return 0.0;
if (N == 0) //when N is 0, or N is completed, return 1
return 1.0;
double probability = 0.0;
probability += matProb(m, n, x - 1, y, N - 1) * 0.25; //move left
probability += matProb(m, n, x, y + 1, N - 1) * 0.25; //move up
probability += matProb(m, n, x + 1, y, N - 1) * 0.25; //move right
probability += matProb(m, n, x, y - 1, N - 1) * 0.25; //move down
return probability;
}
int main() {
int m = 7, n = 8;
int x = 1, y = 1;
int N = 4;
cout << "Matrix Probability is " << matProb(m, n, x, y, N);
}출력
Matrix Probability is 0.664062
위 내용은 행렬 확률 문제인가요?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7467
7467
 15
15
 1376
1376
 52
52
 77
77
 11
11
 46
46
 19
19
 18
18
 20
20
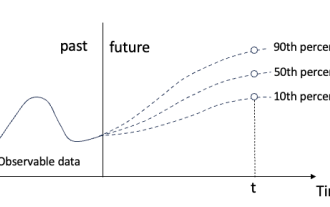 시계열 확률 예측을 위한 분위수 회귀
May 07, 2024 pm 05:04 PM
시계열 확률 예측을 위한 분위수 회귀
May 07, 2024 pm 05:04 PM
원본 내용의 의미를 바꾸지 말고 내용을 미세 조정하고 내용을 다시 작성하고 계속하지 마십시오. "분위수 회귀는 이러한 요구를 충족하여 정량화된 확률로 예측 구간을 제공합니다. 이는 특히 응답 변수의 조건부 분포에 관심이 있는 경우 예측 변수와 응답 변수 간의 관계를 모델링하는 데 사용되는 통계 기술입니다. 기존 회귀와 달리 분위수 회귀는 조건부 평균보다는 반응 변수의 조건부 크기를 추정하는 데 중점을 둡니다. "그림 (A): 분위수 회귀 분위수 회귀의 개념은 추정입니다. 회귀 변수 집합 X와 설명된 변수 Y의 분위수. 기존 회귀모형은 실제로 설명변수와 설명변수의 관계를 연구하기 위한 방법이다. 그들은 설명 변수와 설명 변수 사이의 관계에 중점을 둡니다.
 인공지능의 역사와 매트릭스 탐구: 인공지능 튜토리얼(2)
Nov 20, 2023 pm 05:25 PM
인공지능의 역사와 매트릭스 탐구: 인공지능 튜토리얼(2)
Nov 20, 2023 pm 05:25 PM
이 시리즈의 첫 번째 기사에서는 인공 지능, 머신 러닝, 딥 러닝, 데이터 과학 등의 연관성과 차이점에 대해 논의했습니다. 또한 전체 시리즈에서 사용할 프로그래밍 언어, 도구 등에 대해 몇 가지 어려운 선택을 했습니다. 마지막으로 약간의 행렬 지식도 소개했습니다. 이번 글에서는 인공지능의 핵심인 매트릭스에 대해 심도있게 논의해보겠습니다. 그런데 그 전에 먼저 인공지능의 역사를 이해해 볼까요? 왜 인공지능의 역사를 이해해야 할까요? 역사상 수많은 AI 붐이 있었지만, AI의 잠재력에 대한 큰 기대는 실현되지 못한 경우가 많았다. 인공지능의 역사를 이해하면 이 인공지능의 물결이 기적을 일으킬지 아니면 터질 또 다른 거품일지 알 수 있습니다. 우리를
 클러스터링 알고리즘의 클러스터링 효과 평가 문제
Oct 10, 2023 pm 01:12 PM
클러스터링 알고리즘의 클러스터링 효과 평가 문제
Oct 10, 2023 pm 01:12 PM
클러스터링 알고리즘에서 클러스터링 효과 평가 문제에는 특정 코드 예제가 필요합니다. 클러스터링은 데이터를 클러스터링하여 유사한 샘플을 하나의 범주로 그룹화하는 비지도 학습 방법입니다. 클러스터링 알고리즘에서는 클러스터링의 효과를 어떻게 평가하는가가 중요한 문제입니다. 이 기사에서는 일반적으로 사용되는 몇 가지 클러스터링 효과 평가 지표를 소개하고 해당 코드 예제를 제공합니다. 1. 클러스터링 효과 평가 지수 실루엣 계수 실루엣 계수는 표본의 근접성 및 다른 클러스터와의 분리 정도를 계산하여 클러스터링 효과를 평가합니다.
 일반적인 iPhone 문제를 진단하는 방법을 가르쳐주세요.
Dec 03, 2023 am 08:15 AM
일반적인 iPhone 문제를 진단하는 방법을 가르쳐주세요.
Dec 03, 2023 am 08:15 AM
강력한 성능과 다재다능한 기능으로 잘 알려진 iPhone은 복잡한 전자 장치에서 흔히 발생하는 문제인 가끔씩 발생하는 문제나 기술적인 어려움으로부터 자유롭지 않습니다. iPhone 문제를 경험하면 실망스러울 수 있지만 일반적으로 알람은 필요하지 않습니다. 이 종합 가이드에서는 iPhone 사용과 관련하여 가장 일반적으로 직면하는 문제 중 일부를 쉽게 설명하는 것을 목표로 합니다. 당사의 단계별 접근 방식은 이러한 일반적인 문제를 해결하는 데 도움을 주고 장비를 최상의 작동 순서로 되돌릴 수 있는 실용적인 솔루션과 문제 해결 팁을 제공하도록 설계되었습니다. 결함이 있거나 더 복잡한 문제에 직면하더라도 이 문서는 문제를 효과적으로 해결하는 데 도움이 될 수 있습니다. 일반적인 문제 해결 팁 특정 문제 해결 단계를 진행하기 전에 다음은 몇 가지 유용한 정보입니다.
 jQuery가 양식 요소 값을 얻을 수 없는 문제를 해결하는 방법
Feb 19, 2024 pm 02:01 PM
jQuery가 양식 요소 값을 얻을 수 없는 문제를 해결하는 방법
Feb 19, 2024 pm 02:01 PM
jQuery.val()을 사용할 수 없는 문제를 해결하려면 구체적인 코드 예제가 필요합니다. 프론트 엔드 개발자에게는 jQuery를 사용하는 것이 일반적인 작업 중 하나입니다. 그중에서도 .val() 메서드를 사용하여 양식 요소의 값을 가져오거나 설정하는 것은 매우 일반적인 작업입니다. 그러나 특정한 경우에는 .val() 메서드를 사용하지 못하는 문제가 발생할 수 있습니다. 이 문서에서는 몇 가지 일반적인 상황과 해결 방법을 소개하고 구체적인 코드 예제를 제공합니다. 문제 설명 jQuery를 사용하여 프런트 엔드 페이지를 개발할 때 때때로 다음과 같은 문제가 발생할 수 있습니다.
 다차원 배열을 사용하여 두 행렬을 곱하는 Python 프로그램
Sep 11, 2023 pm 05:09 PM
다차원 배열을 사용하여 두 행렬을 곱하는 Python 프로그램
Sep 11, 2023 pm 05:09 PM
행렬은 행과 열로 배열된 숫자의 집합입니다. m행과 n열로 구성된 행렬을 mXn 행렬이라고 하며, m과 n을 차원이라고 합니다. 행렬은 목록이나 NumPy 배열을 사용하여 Python에서 만든 2차원 배열입니다. 일반적으로 행렬 곱셈은 첫 번째 행렬의 행과 두 번째 행렬의 열을 곱하여 수행할 수 있습니다. 여기서 첫 번째 행렬의 열 개수는 두 번째 행렬의 행 개수와 같아야 합니다. 입력 및 출력 시나리오 두 개의 행렬 A와 B가 있다고 가정합니다. 이 두 행렬의 차원은 각각 2X3과 3X2입니다. 곱셈 후 결과 행렬은 2개의 행과 1개의 열을 갖게 됩니다. [b1,b2][a1,a2,a3]*[b3,b4]=[a1*b1+a2*b2+a3*a3][a4,a5,a6][b5,b6][a4*b2+a
 머신러닝 모델의 일반화 능력 문제
Oct 08, 2023 am 10:46 AM
머신러닝 모델의 일반화 능력 문제
Oct 08, 2023 am 10:46 AM
기계 학습 모델의 일반화 기능에는 특정 코드 예제가 필요합니다. 기계 학습의 개발 및 적용이 점점 더 널리 보급됨에 따라 사람들은 기계 학습 모델의 일반화 기능에 점점 더 많은 관심을 기울이고 있습니다. 일반화 능력은 레이블이 지정되지 않은 데이터에 대한 기계 학습 모델의 예측 능력을 의미하며, 현실 세계에서 모델의 적응성으로도 이해될 수 있습니다. 좋은 머신러닝 모델은 높은 일반화 능력을 갖추고 새로운 데이터에 대해 정확한 예측을 할 수 있어야 합니다. 그러나 실제 응용에서는 훈련 세트에서는 잘 수행되지만 테스트 세트에서는 실패하거나 실제 모델에서 실패하는 모델을 자주 접하게 됩니다.
 약한 지도 학습의 라벨 획득 문제
Oct 08, 2023 am 09:18 AM
약한 지도 학습의 라벨 획득 문제
Oct 08, 2023 am 09:18 AM
약한 지도 학습의 라벨 획득 문제에는 특정 코드 예제가 필요합니다. 소개: 약한 지도 학습은 훈련에 약한 라벨을 사용하는 기계 학습 방법입니다. 기존 지도 학습과 달리 약한 지도 학습은 각 샘플에 정확한 라벨이 필요한 것이 아니라 모델을 훈련하는 데 더 적은 수의 라벨만 사용하면 됩니다. 그러나 약한 지도 학습에서는 약한 레이블로부터 유용한 정보를 정확하게 얻는 방법이 핵심 문제입니다. 이 기사에서는 약한 지도 학습의 레이블 획득 문제를 소개하고 구체적인 코드 예제를 제공합니다. 약한 지도 학습의 라벨 획득 문제 소개:




