C 프로그램에서 다음을 중국어로 번역합니다. 정삼각형에 내접한 원에 내접한 정사각형의 면적은 얼마입니까?
여기서는 정사각형의 면적이 원에 내접되어 있고 원이 정삼각형에 내접되어 있음을 볼 수 있습니다. 정사각형의 변은 "a"입니다. 원의 반지름은 "r"이고 육각형의 변은 "A"입니다. 차트는 아래와 같습니다.
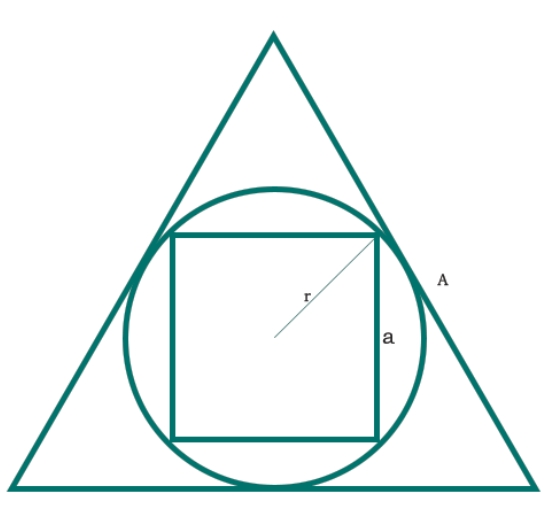
우리는 정삼각형의 내접원의 반경이 삼각형의 내부 반경이라는 것을 알고 있습니다. 따라서 값은 -
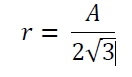
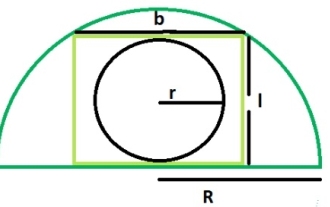
이므로 정사각형의 대각선은 -

이므로 정사각형의 면적은 -

Example
#include <iostream>
#include <cmath>
using namespace std;
float area(float A) { //A is the side of the triangle
if (A < 0) //if the value is negative it is invalid
return -1;
float d = A / sqrt(3);
float area = 0.5*d*d;
return area;
}
int main() {
float side = 10;
cout << "Area is: " << area(side);
}Output
Area is: 16.6667
위 내용은 C 프로그램에서 다음을 중국어로 번역합니다. 정삼각형에 내접한 원에 내접한 정사각형의 면적은 얼마입니까?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7470
7470
 15
15
 1377
1377
 52
52
 77
77
 11
11
 48
48
 19
19
 19
19
 29
29
 반원에 새겨진 직사각형 안에 원의 면적은 얼마입니까?
Sep 13, 2023 am 08:45 AM
반원에 새겨진 직사각형 안에 원의 면적은 얼마입니까?
Sep 13, 2023 am 08:45 AM
직사각형에 내접하는 원은 직사각형의 긴 변에 접합니다. 즉, 그 길이는 원에 접합니다. 반원에 내접한 직사각형은 반원호의 두 점과 접촉합니다. 직사각형의 너비는 원의 지름과 같습니다. R이 반원의 반지름인 경우. 직사각형의 길이 = √2R/2 직사각형의 폭 = R/√2 내접원의 반지름은 r = b/2 = R/2√2 이 공식을 사용하여 반원에 내접하는 직사각형을 계산할 수 있습니다. 원의 면적,area = (π*r2)=π*R/8 예제 데모 #include<stdio.h>intmain(){&
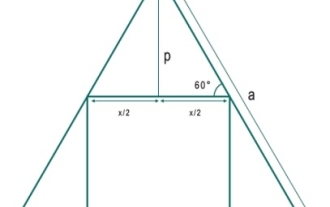 정삼각형에 내접할 수 있는 가장 큰 정사각형은 무엇입니까?
Sep 22, 2023 pm 06:21 PM
정삼각형에 내접할 수 있는 가장 큰 정사각형은 무엇입니까?
Sep 22, 2023 pm 06:21 PM
여기서 우리는 정삼각형에 내접할 수 있는 가장 큰 정사각형의 면적을 볼 수 있습니다. 삼각형의 변의 길이는 'a'이고 정사각형의 변의 길이는 x입니다. 삼각형의 변 길이 'a'는 − 따라서 x는 −입니다. 예 #include<iostream>#include<cmath>usingnamespacestd;floatareaSquare(floata){//aissideoftriangle if(a<0)//ifaisnegative,thenthisisi
 C 프로그램에서 마름모 안에 새겨진 원의 넓이는 얼마입니까?
Sep 01, 2023 pm 09:29 PM
C 프로그램에서 마름모 안에 새겨진 원의 넓이는 얼마입니까?
Sep 01, 2023 pm 09:29 PM
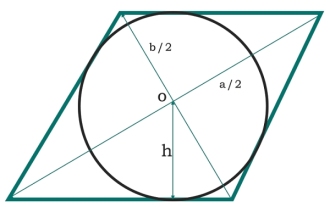
여기에서는 마름모에 새겨진 원의 면적을 볼 수 있습니다. 마름모의 대각선은 각각 'a'와 'b'입니다. 원의 반지름은 h입니다. 두 개의 대각선이 네 개의 동일한 삼각형을 형성합니다. 모든 삼각형은 직각삼각형이므로 그 넓이는 다음과 같습니다. - 마름모의 각 변은 빗변입니다. - 따라서 원의 넓이는 다음과 같습니다. - 예#include<iostream>#include<cmath>usingnamespacestd;floatarea(floata,floatb ) { if(a<0||b<0)//ifthevaluesren
 C 프로그램에서 다음을 중국어로 번역합니다. 정삼각형에 내접한 원에 내접한 정사각형의 면적은 얼마입니까?
Aug 31, 2023 pm 12:25 PM
C 프로그램에서 다음을 중국어로 번역합니다. 정삼각형에 내접한 원에 내접한 정사각형의 면적은 얼마입니까?
Aug 31, 2023 pm 12:25 PM
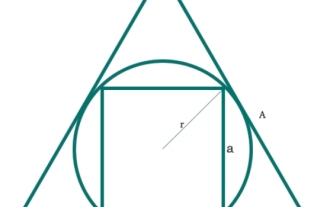
여기서 우리는 정사각형의 면적이 원에 내접되어 있고 원이 정삼각형에 내접되어 있음을 볼 수 있습니다. 정사각형의 변은 "a"입니다. 원의 반지름은 "r"이고 육각형의 변은 "A"입니다. 차트는 아래와 같습니다. 따라서 정사각형의 대각선은 - 정사각형의 면적은 - 예 #include<iostream>#include<cmath>usingnamespacestd;floatarea(floatA){//Aisthesideofthetriangle if(A<0)//ifthevalueisne
 Java에서 사각형에 새겨진 원의 면적 찾기
Aug 19, 2023 pm 04:53 PM
Java에서 사각형에 새겨진 원의 면적 찾기
Aug 19, 2023 pm 04:53 PM
원은 모서리가 없는 2차원 다이어그램 주위에 있습니다. 모든 원은 원점이 있고 원 위의 모든 점은 원점으로부터 동일한 거리를 유지합니다. 원점과 원점 사이의 거리는 원의 반경으로 알려져 있습니다.
 C 프로그래밍에서 원의 넓이 구하기
Aug 25, 2023 pm 10:57 PM
C 프로그래밍에서 원의 넓이 구하기
Aug 25, 2023 pm 10:57 PM
원은 닫힌 그림입니다. 원의 모든 점은 원 내부의 점에서 등거리에 있습니다. 중심점을 원의 중심이라고 합니다. 한 점에서 원의 중심까지의 거리를 반지름이라고 합니다. 면적은 닫힌 그림의 크기 범위를 정량적으로 표현한 것입니다. 원의 면적은 원의 치수 내에 둘러싸인 면적입니다. 원의 면적을 계산하는 공식, Area=π*r*r 면적을 계산하기 위해 원의 반경을 입력으로 주고 공식을 사용하여 면적을 계산합니다. 알고리즘 STEP1: Takeradiusasinputfromtheuserusingstdinput.STEP2 : 원의 면적을 계산합니다. 면적=(
 반원에 새겨진 직사각형 안에 원의 면적은 얼마입니까?
Sep 04, 2023 pm 11:33 PM
반원에 새겨진 직사각형 안에 원의 면적은 얼마입니까?
Sep 04, 2023 pm 11:33 PM
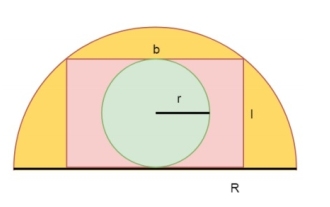
주어진 반원을 생각해 봅시다. 반경은 R입니다. 길이가 l이고 너비가 b인 직사각형이 반원에 새겨져 있습니다. 이제 반지름이 r인 원이 직사각형에 새겨져 있습니다. 안쪽 원의 넓이를 구해야 합니다. 반원에 내접할 수 있는 가장 큰 직사각형의 길이는 l이고 폭은 b이므로 l과 b의 방정식은 다음과 같습니다. 이제 직사각형에 내접할 수 있는 가장 큰 원의 반지름은 r입니다. 다음과 같습니다 -
 직각삼각형인 정사각형에 새겨진 가장 큰 루에로삼각형은 무엇입니까?
Sep 04, 2023 pm 10:29 PM
직각삼각형인 정사각형에 새겨진 가장 큰 루에로삼각형은 무엇입니까?
Sep 04, 2023 pm 10:29 PM
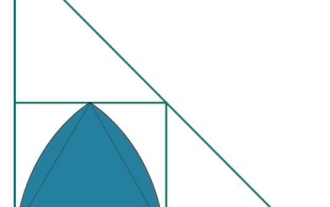
여기서 우리는 정사각형에 내접된 가장 큰 Reuleaux 삼각형의 면적을 볼 수 있으며, 이는 다시 직각 삼각형에 내접됩니다. 정사각형의 한 변의 길이는 'a'입니다. Reuleaux 삼각형의 높이는 x입니다. 삼각형의 밑변은 b, 높이는 l, 빗변은 h입니다. 우리는 높이가 l이고 밑변이 b인 직각삼각형에 내접하는 정사각형이 한 변의 길이를 갖는다는 것을 알고 있습니다. 릴로삼각형의 높이는 a와 같습니다. 따라서 a=x입니다. 따라서 Reuleaux 삼각형의 면적은 - 예#include<iostream>#include<cmath>usingnamespacestd;fl




