C 프로그램에서 다음을 중국어로 번역합니다. 정삼각형에 새겨진 원 안의 정사각형의 면적은 얼마입니까?
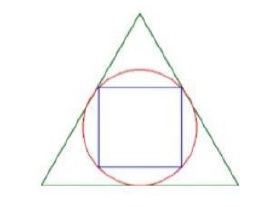
정삼각형에 내접한 원에 내접한 정사각형의 넓이를 구하세요. 정삼각형에 내접하는 원의 반지름은 a/(2√3)입니다.
원의 지름은 정사각형의 대각선, d = 2 * r = a/ √3
정사각형의 면적 공식은 ½ d2,
A = 0.5 * d2입니다. A = (1/2) * (a2) / (3) = (a2/6)
예
#include <iostream>
using namespace std;
int main() {
float area,a = 10;
area = (a*a) / 6;
cout <<"area = "<<area<< endl;
return 0;
}출력
area = 16.6667
위 내용은 C 프로그램에서 다음을 중국어로 번역합니다. 정삼각형에 새겨진 원 안의 정사각형의 면적은 얼마입니까?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7629
7629
 15
15
 1389
1389
 52
52
 89
89
 11
11
 70
70
 19
19
 31
31
 141
141
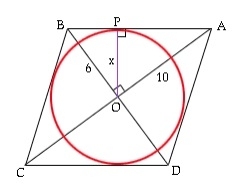 마름모에 새겨진 원의 넓이는 얼마입니까?
Sep 05, 2023 am 08:25 AM
마름모에 새겨진 원의 넓이는 얼마입니까?
Sep 05, 2023 am 08:25 AM
마름모의 내접원은 네 변과 네 끝점에 접합니다. 마름모의 변은 원에 접합니다. 여기서 r은 a와 주어진 값의 대각선을 사용하여 구한 반지름입니다. 이제 면적 삼각형 AOB = ½*OA*OB = ½*AB*r(둘 다 공식 ½*b*h 사용)입니다. ½*a/2*b/2=½*(√(a2/4+b2/4))*ra*b/8=√(a2+b2)*r/4r=a*b/2√(a2 +b2) 원 면적 = π*r*r=π*(a2*b2)/4(a2support>+b2) 마름모 5와 10의 대각선의 예. 면적은 15.700000입니다. 예시 코드 실시간 데모 #include<stdio.h>intma
 Java에서 사각형에 새겨진 원의 면적 찾기
Aug 19, 2023 pm 04:53 PM
Java에서 사각형에 새겨진 원의 면적 찾기
Aug 19, 2023 pm 04:53 PM
원은 모서리가 없는 2차원 다이어그램 주위에 있습니다. 모든 원은 원점이 있고 원 위의 모든 점은 원점으로부터 동일한 거리를 유지합니다. 원점과 원점 사이의 거리는 원의 반경으로 알려져 있습니다.
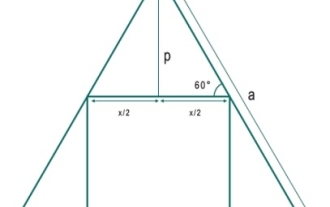 정삼각형에 내접할 수 있는 가장 큰 정사각형은 무엇입니까?
Sep 22, 2023 pm 06:21 PM
정삼각형에 내접할 수 있는 가장 큰 정사각형은 무엇입니까?
Sep 22, 2023 pm 06:21 PM
여기서 우리는 정삼각형에 내접할 수 있는 가장 큰 정사각형의 면적을 볼 수 있습니다. 삼각형의 변의 길이는 'a'이고 정사각형의 변의 길이는 x입니다. 삼각형의 변 길이 'a'는 − 따라서 x는 −입니다. 예 #include<iostream>#include<cmath>usingnamespacestd;floatareaSquare(floata){//aissideoftriangle if(a<0)//ifaisnegative,thenthisisi
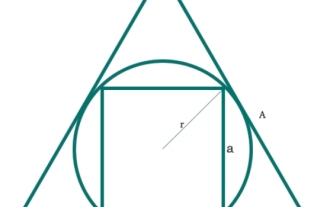 C 프로그램에서 다음을 중국어로 번역합니다. 정삼각형에 내접한 원에 내접한 정사각형의 면적은 얼마입니까?
Aug 31, 2023 pm 12:25 PM
C 프로그램에서 다음을 중국어로 번역합니다. 정삼각형에 내접한 원에 내접한 정사각형의 면적은 얼마입니까?
Aug 31, 2023 pm 12:25 PM
여기서 우리는 정사각형의 면적이 원에 내접되어 있고 원이 정삼각형에 내접되어 있음을 볼 수 있습니다. 정사각형의 변은 "a"입니다. 원의 반지름은 "r"이고 육각형의 변은 "A"입니다. 차트는 아래와 같습니다. 따라서 정사각형의 대각선은 - 정사각형의 면적은 - 예 #include<iostream>#include<cmath>usingnamespacestd;floatarea(floatA){//Aisthesideofthetriangle if(A<0)//ifthevalueisne
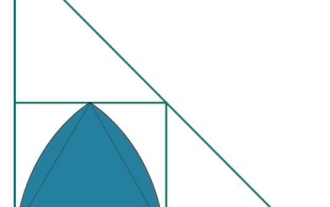 직각삼각형인 정사각형에 새겨진 가장 큰 루에로삼각형은 무엇입니까?
Sep 04, 2023 pm 10:29 PM
직각삼각형인 정사각형에 새겨진 가장 큰 루에로삼각형은 무엇입니까?
Sep 04, 2023 pm 10:29 PM
여기서 우리는 정사각형에 내접된 가장 큰 Reuleaux 삼각형의 면적을 볼 수 있으며, 이는 다시 직각 삼각형에 내접됩니다. 정사각형의 한 변의 길이는 'a'입니다. Reuleaux 삼각형의 높이는 x입니다. 삼각형의 밑변은 b, 높이는 l, 빗변은 h입니다. 우리는 높이가 l이고 밑변이 b인 직각삼각형에 내접하는 정사각형이 한 변의 길이를 갖는다는 것을 알고 있습니다. 릴로삼각형의 높이는 a와 같습니다. 따라서 a=x입니다. 따라서 Reuleaux 삼각형의 면적은 - 예#include<iostream>#include<cmath>usingnamespacestd;fl
 육각형에 새겨진 원 안의 정사각형의 면적을 계산하는 C 프로그램
Aug 28, 2023 pm 08:41 PM
육각형에 새겨진 원 안의 정사각형의 면적을 계산하는 C 프로그램
Aug 28, 2023 pm 08:41 PM
정육각형이 내접한 원에 내접한 정사각형이 있을 때 정사각형의 넓이를 구해야 하고, 이를 위해서는 정사각형의 한 변의 길이와 정육각형의 한 변의 길이 사이의 관계를 찾아야 합니다. . 정육각형의 내접원 반지름의 수학식은 r=A√3/2입니다. 정사각형의 대각선은 원의 지름과 같으므로 반지름과 변의 길이 사이의 관계는 다음과 같습니다. 정육각형에 따른 a=√r 의 변의 길이, a=√3A/√2, 즉 정사각형의 면적,area=a2=(√3A/√2)2 예시 #include<stdio. h>#포함
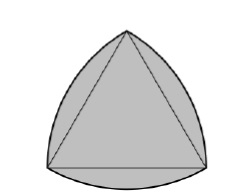 C에서는 정사각형 내부의 가장 큰 Reuleaux 삼각형입니다.
Sep 07, 2023 pm 12:29 PM
C에서는 정사각형 내부의 가장 큰 Reuleaux 삼각형입니다.
Sep 07, 2023 pm 12:29 PM
룰 삼각형은 세 개의 디스크가 교차하여 형성된 모양으로, 각 디스크의 중심은 다른 두 디스크의 경계에 있습니다. 그 경계는 일정한 너비의 곡선으로, 원 자체를 제외하면 가장 단순하고 잘 알려진 곡선이다. 폭이 일정하다는 것은 두 개의 평행한 지지선 사이의 간격이 방향에 관계없이 동일하다는 것을 의미합니다. 직경이 모두 동일하기 때문입니다. Lule 삼각형의 경계는 정삼각형을 기반으로 하는 일정한 너비의 곡선입니다. 모서리의 모든 점은 반대쪽 꼭지점에서 등거리에 있습니다. Lule 삼각형을 만드는 공식은 곡선이 정삼각형을 기반으로 하고 삼각형의 변의 길이가 h인 경우 Lule 삼각형의 면적은 A=(π*h2)/2–2*(입니다. 아리아오
 C 프로그램에서 다음을 중국어로 번역합니다. 정육각형에 내접한 원에 내접한 정사각형의 면적은 얼마입니까?
Sep 05, 2023 pm 09:33 PM
C 프로그램에서 다음을 중국어로 번역합니다. 정육각형에 내접한 원에 내접한 정사각형의 면적은 얼마입니까?
Sep 05, 2023 pm 09:33 PM
여기에서 우리는 하나의 원에 내접된 사각형의 영역과 육각형에 내접된 원의 영역을 볼 수 있습니다. 사각형의 변은 'a'입니다. 원의 반경은 'r'이고 육각형의 변은 'A'입니다. 다이어그램은 b와 같습니다.




