C++에서는 접두사에 -1을 곱하여 배열의 합을 최대화합니다.

정수 배열이 있고 작업은 먼저 배열의 접두사를 가져온 다음 -1을 곱하고, 두 번째로 배열의 접두사 합계를 계산하고 마지막으로 생성된 접두사에서 최대 합계를 찾는 것입니다. 정렬.
접두사 배열은 다음과 같이 생성됩니다.
접두사 배열의 첫 번째 요소 prefixArray[0] = 배열의 첫 번째 요소
접두사 배열의 두 번째 요소 prefixArray[1] = prefixArray[0] + arr [1]
접두사 배열의 세 번째 요소 prefixArray[2] = prefixArray[1] + arr[2]
접두사 배열의 네 번째 요소 prefixArray[3] = prefixArray[2] + arr[3] . ..기타.
이 문제의 다양한 입력 및 출력 상황을 살펴보겠습니다. -
For int arr[] = {2, 4, 1, 5, 2}
출력 접두사 배열은 -2 2 3입니다. 8 10 접두사에 -1을 곱하여 배열의 합을 최대화합니다. 21
Explanation - 정수 배열이 있습니다. 먼저 배열의 접두사인 2를 얻고 여기에 -1을 곱합니다. 따라서 새 배열은 {-2, 4, 1, 5, 2}입니다. 이제 접두사 배열의 최대 합을 구성하겠습니다.
접두사 배열은 {-2, 2, 3, 8, 10}입니다. 마지막 단계는 합계를 -2+2+3+8+`0 = 21로 최대화하는 것입니다. 이는 최종 출력입니다.In - int arr[] = {-1, 4, 2, 1, -9, 6};
출력 - 접두사 배열은 다음과 같습니다. 1 5 7 8 -1 5 -1을 곱한 배열, 최대화된 배열의 합은 다음과 같습니다. 19
Explanation- 정수 배열이 있습니다. 먼저 배열의 접두사 -1에 -1을 곱합니다. 따라서 새 배열은 {1, 4, 2, 1, -9, 6}이 됩니다. 이제 우리는 형성할 것이다 접두사 배열은 {1, 5, 7, 8, -1, 5}입니다. 마지막 단계는 합을 1+5+8+5 = 19로 최대화하는 것이며, 이것이 최종 출력입니다.
아래 프로그램에서 사용한 방법은 다음과 같습니다. -
정수 배열과 임시 변수 x를 -1로 선언한 후 arr[0]을 arr[0] * x로 설정합니다.
배열의 크기를 계산합니다. 접두사 배열 prefix_array[size]를 선언합니다. 주어진 배열에 대한 접두사 배열을 생성하려면 create_prefix_arr(arr, size, prefix_array) 함수를 호출하세요. 접두사 배열 인쇄
는 배열의 최대 합계를 저장하는 maximum_sum(prefix_array, size) 함수를 호출합니다.
-
함수 내에서 void create_prefix_arr(int arr[], int size, int prefix_array[])
prefix_array[0]을 arr[0]으로 설정하세요.
배열 크기가 나올 때까지 i부터 0까지 반복을 시작합니다. 루프 내에서 prefix_array[i]를 prefix_array[i-1] + arr[i]로 설정합니다.
-
함수 내부에서 int maximum_sum(int prefix_array[], int size)
임시 변수 temp를 선언하고 -1로 설정합니다.
배열 크기가 나올 때까지 i부터 0까지 반복을 시작합니다. 루프 내에서 temp를 max(temp, prefix_array[i])
배열 arr[temp +1]을 선언하고 배열의 모든 요소를 0으로 초기화합니다.
배열 크기가 나올 때까지 i부터 0까지 반복을 시작합니다. 루프 내에서 임시 변수 max_sum arr[prefix_array[i]]++
을 선언하고 이를 0으로 설정합니다. i>0일 때 루프를 시작하려면 변수 i를 temp
로 선언하세요. arr[i] > 0인지 확인한 다음 max_sum을 max_sum + i로 설정하고 arr[i-1]-- 및 arr[i]--를 설정합니다. 그렇지 않으면 i를 1씩 감소시킵니다.
max_sum을 반환합니다.
예제
#include <bits/stdc++.h>
using namespace std;
#define Max_size 5
//create the prefix array
void create_prefix_arr(int arr[], int size, int prefix_array[]) {
prefix_array[0] = arr[0];
for(int i=0; i<size; i++) {
prefix_array[i] = prefix_array[i-1] + arr[i];
}
}
//find the maximum sum of prefix array
int maximize_sum(int prefix_array[], int size) {
int temp = -1;
for(int i = 0; i < size; i++) {
temp = max(temp, prefix_array[i]);
}
int arr[temp + 1];
memset(arr, 0, sizeof(arr));
for(int i = 0; i < size; i++) {
arr[prefix_array[i]]++;
}
int max_sum = 0;
int i = temp;
while(i>0) {
if(arr[i] > 0) {
max_sum = max_sum + i;
arr[i-1]--;
arr[i]--;
} else {
i--;
}
}
return max_sum;
}
int main() {
int arr[] = {2, 4, 1, 5, 2};
int x = -1;
arr[0] = arr[0] * x;
int size = sizeof(arr) / sizeof(arr[0]);
int prefix_array[size];
//call function to create a prefix array
create_prefix_arr(arr, size, prefix_array);
//print the prefix array
cout<<"Prefix array is: ";
for(int i = 0; i < size; i++) {
cout << prefix_array[i] << " ";
}
//print the maximum sum of prefix array
cout<<"\nMaximize the sum of array by multiplying prefix of array with -1 are:" <<maximize_sum(prefix_array, size);
return 0;
}Output
위 코드를 실행하면 다음과 같은 출력이 생성됩니다
Prefix array is: -2 2 3 8 10 Maximize the sum of array by multiplying prefix of array with -1 are: 21
위 내용은 C++에서는 접두사에 -1을 곱하여 배열의 합을 최대화합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7518
7518
 15
15
 1378
1378
 52
52
 81
81
 11
11
 53
53
 19
19
 21
21
 68
68
 C++를 사용하여 N번째 제곱수가 아닌 숫자를 찾는 코드를 작성하세요.
Aug 30, 2023 pm 10:41 PM
C++를 사용하여 N번째 제곱수가 아닌 숫자를 찾는 코드를 작성하세요.
Aug 30, 2023 pm 10:41 PM
우리 모두는 2, 3, 5, 7, 8 등과 같이 어떤 숫자의 제곱도 아닌 숫자를 알고 있습니다. N개의 정사각형이 아닌 숫자가 있으며 모든 숫자를 아는 것은 불가능합니다. 그래서 이 글에서는 제곱이 없는 숫자나 제곱이 아닌 숫자에 대한 모든 것과 C++에서 N번째 제곱이 아닌 숫자를 찾는 방법을 설명할 것입니다. N번째 비제곱수 어떤 숫자가 정수의 제곱인 경우, 그 숫자를 완전제곱수라고 합니다. 완전제곱수의 몇 가지 예는 다음과 같습니다. -1issquareof14issquareof29issquareof316issquareof425issquareof5 숫자가 정수의 제곱이 아닌 경우 해당 숫자를 제곱이 아닌 숫자라고 합니다. 예를 들어, 처음 15개의 정사각형이 아닌 숫자는 -2,3,5,6입니다.
 C 프로그래밍에서 원의 넓이 구하기
Aug 25, 2023 pm 10:57 PM
C 프로그래밍에서 원의 넓이 구하기
Aug 25, 2023 pm 10:57 PM
원은 닫힌 그림입니다. 원의 모든 점은 원 내부의 점에서 등거리에 있습니다. 중심점을 원의 중심이라고 합니다. 한 점에서 원의 중심까지의 거리를 반지름이라고 합니다. 면적은 닫힌 그림의 크기 범위를 정량적으로 표현한 것입니다. 원의 면적은 원의 치수 내에 둘러싸인 면적입니다. 원의 면적을 계산하는 공식, Area=π*r*r 면적을 계산하기 위해 원의 반경을 입력으로 주고 공식을 사용하여 면적을 계산합니다. 알고리즘 STEP1: Takeradiusasinputfromtheuserusingstdinput.STEP2 : 원의 면적을 계산합니다. 면적=(
 C++로 작성된 배열의 오른쪽 회전을 위한 반전 알고리즘
Sep 08, 2023 pm 08:17 PM
C++로 작성된 배열의 오른쪽 회전을 위한 반전 알고리즘
Sep 08, 2023 pm 08:17 PM
이 기사에서는 주어진 배열을 k 요소만큼 오른쪽으로 회전하는 반전 알고리즘에 대해 알아봅니다(예: −Input:arr[]={4,6,2,6,43,7,3,7}). k= 4 출력:{43,7,3,7,4,6,2,6}설명: 배열의 각 요소를 4개 요소별로 오른쪽으로 회전하면 {43,7,3,7,4,6,2,6}이 됩니다.입력:arr[]= {8 ,5,8,2,1,4,9,3},k=3출력:{4,9,3,8,5,8,2,1} 해결책 찾기
 C++를 사용하여 배열의 고유 쌍 수 찾기
Sep 07, 2023 am 11:53 AM
C++를 사용하여 배열의 고유 쌍 수 찾기
Sep 07, 2023 am 11:53 AM
C++의 배열 구문에서 여러 개의 고유한 쌍을 생성하려면 적절한 지식이 필요합니다. 고유 쌍의 수를 찾는 동안 주어진 배열의 모든 고유 쌍을 계산합니다. 즉, 각 쌍이 고유해야 하는 모든 가능한 쌍이 형성될 수 있습니다. 예를 들어 -Input:array[]={5,5,9}Output:4Explanation:Thenumberoffalluniquepairsare(5,5),(5,9),(9,5)and(9,9).Input:array[] = {5,4,3,2,2} 출력: 해결 방법을 찾는 16가지 방법 이 문제를 해결하는 방법에는 두 가지가 있습니다.
 C++를 사용하여 최소값과 최대값이 동일한 하위 배열의 수를 찾는 코드를 작성하세요.
Aug 25, 2023 pm 11:33 PM
C++를 사용하여 최소값과 최대값이 동일한 하위 배열의 수를 찾는 코드를 작성하세요.
Aug 25, 2023 pm 11:33 PM
이번 글에서는 C++를 이용하여 최대값과 최소값이 같은 부분배열의 개수를 찾는 문제를 해결해보겠습니다. 다음은 문제의 예입니다. −Input:array={2,3,6,6,2,4,4,4}Output:12Explanation:{2},{3},{6},{6}, {2 },{4},{4},{4},{6,6},{4,4},{4,4}및{4,4,4}는 동일한 최대 및 최소 요소로 구성할 수 있는 하위 배열입니다.입력:배열={3, 3, 1,5,
 C++로 작성되어 집합의 반사 관계 수를 찾습니다.
Aug 26, 2023 pm 08:17 PM
C++로 작성되어 집합의 반사 관계 수를 찾습니다.
Aug 26, 2023 pm 08:17 PM
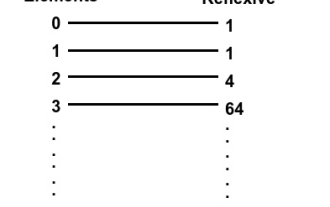
이 기사에서는 집합에서 반사 관계를 찾는 방법을 설명합니다. 이 문제에서는 숫자 n과 n개의 자연수 집합이 주어지며 반사 관계의 수를 결정해야 합니다. 재귀 관계 - 집합 A의 모든 'a'에 대해 (a, a)가 관계 R에 속하면 관계 R은 집합 A에 대한 재귀 관계라고 합니다. 예를 들어 -Input:x=1Output:1Explanation:set={1},reflexiverelationsonA*A:{{1}}Input:x=2Output:4Explanation:set={1,2},reflexiverelationsonA*
 C++를 사용하여 주어진 크기로 역방향 이중 연결 목록 그룹화
Sep 04, 2023 am 09:49 AM
C++를 사용하여 주어진 크기로 역방향 이중 연결 목록 그룹화
Sep 04, 2023 am 09:49 AM
이 문제에서는 연결 리스트의 헤드에 대한 포인터와 정수 k가 제공됩니다. 크기가 k인 그룹에서는 연결된 목록을 뒤집어야 합니다. 예를 들어 -Input:1<->2<->3<->4<->5(이중 링크 목록),k=3Output:3<->2<->1<->5<->4 솔루션 찾기 방법 이 문제에서는 이 문제를 해결하기 위한 재귀 알고리즘을 공식화합니다. 이 방법에서는 재귀를 사용하고 재귀를 사용하여 문제를 해결합니다. 예#include<iostream&
 C++로 작성된 배열 회전 반전 알고리즘
Aug 28, 2023 pm 11:13 PM
C++로 작성된 배열 회전 반전 알고리즘
Aug 28, 2023 pm 11:13 PM
주어진 문제에는 배열이 있고 −Input:arr[]=[1,2,3,4,5,6,7], d=2Output과 같은 반전 알고리즘을 사용하여 d 요소만큼 배열을 회전해야 합니다. arr[]=[3,4,5,6,7,1,2]설명: 보시다시피 이 배열을 d=2로 회전해야 하지만 우리의 주요 작업은 반전 기술을 사용하여 이를 달성하는 것입니다. 우리는 반전 기술을 사용하여 배열 회전에 대한 몇 가지 계산을 수행하고 결론을 내렸습니다.




