비순환 그래프가 주어지면 각 깊이에서 요소의 최소 합을 계산합니다.

사이클이나 루프가 포함되지 않은 그래프를 비순환 그래프라고 합니다. 트리는 모든 노드가 다른 고유 노드에 연결되는 비순환 그래프입니다. 비순환 그래프는 비순환 그래프라고도 합니다.

순환 그래프와 비순환 그래프의 차이점 -

의 중국어 번역은 입니다.

Cycle Graph	Cycle Graph	비순환 그래프
그래프는 닫힌 루프를 형성합니다.	차트는 폐쇄 루프를 형성하지 않습니다.
딥 루프는 차트에 포함되지 않습니다	차트는 모든 깊이를 담고 있습니다.

예 1

순환 그래프의 예를 들어보겠습니다 −

폐쇄 루프가 존재하면 순환 그래프가 형성됩니다.

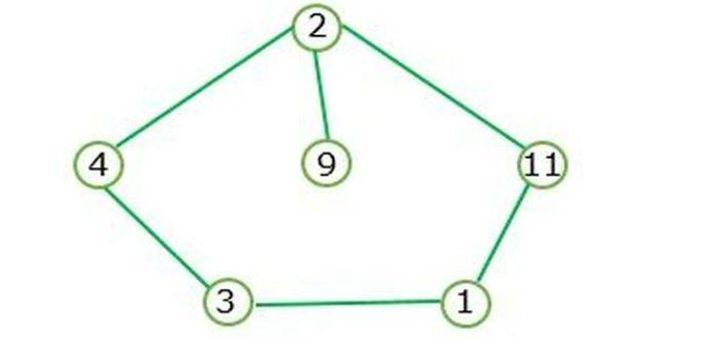
그림 I은 주기 그래프를 나타내며 깊이 노드를 포함하지 않습니다.

예 2

는 다음과 같이 번역됩니다.

예 2

비순환 그래프의 예를 들어 설명하겠습니다.

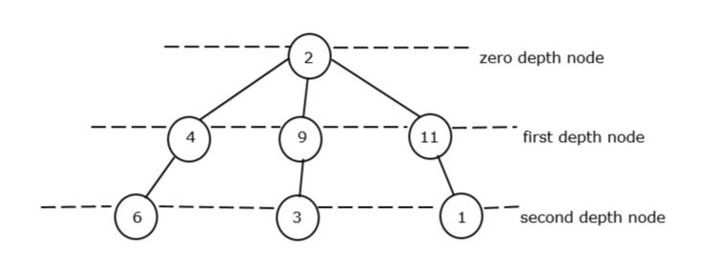
트리의 루트 노드를 제로 깊이 노드라고 합니다. 그림 II에는 깊이가 0인 루트가 하나만 있으며, 이는 2입니다. 따라서 최소 깊이가 0인 노드로 간주됩니다.

첫 번째 깊이 노드에는 4, 9, 1과 같은 3개의 노드 요소가 있지만 가장 작은 요소는 4입니다.

두 번째 깊이 노드에는 다시 6, 3, 1과 같은 3개의 노드 요소가 있지만 최소 요소는 1입니다.

전체 깊이 노드가 어떻게 파생되는지 알 수 있습니다.

총 깊이 노드 = Zero_Depth 노드의 최소값 + First_Depth 노드의 최소값 + Zero_Depth 노드의 최소값

총 깊이 노드 = 2 + 4 + 3 = 9. 따라서 9는 비순환 그래프의 총 최소 합입니다.

문법

으아악

• struct − 이 키워드는 구조 데이터 유형을 나타내는 데 사용됩니다.

• name_of_struct - 구조에 대한 이름을 제공합니다.

• 구조체는 다양한 관련 변수를 한 곳에 모아 놓은 것입니다.

으아악 으아악

매개변수

C++의 쌍 대기열 -

• 이것은 서로 다른 두 데이터 유형의 대기열 쌍을 결합하기 위한 일반 STL 템플릿입니다. 대기열 쌍은 유틸리티 헤더 파일 아래에 있습니다.

• Queue_of_pair - 쌍에 이름을 지정합니다.

• make_pair() - 두 요소로 쌍 개체를 구성하는 데 사용됩니다.

으아악

매개변수

• name_of_queue - 대기열 이름을 지정하고 있습니다.

• push() − 대기열 헤드의 일부인 미리 정의된 메서드입니다. 푸시 메서드는 요소나 값을 삽입하는 데 사용됩니다.

으아악

매개변수

• name_of_queue − 대기열에 이름을 지정합니다.

• pop() - 큐 헤더 파일에 속하는 미리 정의된 메소드로 전체 요소나 값을 삭제하는 데 사용됩니다.

알고리즘

• 프로그램 헤더 파일, 즉 'iostream', 'climits', 'utility', 및 'queue'를 시작합니다.

• 우리는 노드 값을 얻기 위해 정수 값 "val"을 사용하여 구조 "tree_node"를 생성하고 있습니다. 그런 다음 주어진 데이터로 tree_node 포인터를 생성하여 왼쪽 자식 노드와 오른쪽 자식 노드를 초기화하여 값을 저장합니다. 다음으로 int x가 인수로 전달되는 tree_node 함수를 생성하고 'val' 정수와 동일한지 확인하고 왼쪽 및 오른쪽 하위 노드를 null 에 할당합니다.

• 이제 각 깊이에서 최소 합계를 찾기 위해 정수 값을 인수로 받아들이는 함수 minimum_sum_at_each_length()를 정의하겠습니다. if 문을 사용하여 트리의 루트 값이 비어 있는지 확인하고 비어 있으면 0을 반환합니다.

• 두 값을 결합하기 위해 STL(Standard Template Library)의 대기열 쌍을 생성하고 있습니다.

• 두 가지 메소드, 즉 push() 및 make_pair()를 한 쌍으로 사용하는 q라는 대기열 변수를 생성합니다. 이 두 가지 방법을 사용하여 값을 삽입하고 두 쌍의 객체를 구성합니다.

• 현재 합계를 추가로 찾고 전체 최소 합계를 찾는 데 사용되는 'present_length', 'present_sum' 및 'totalSum'이라는 세 가지 변수를 초기화하고 있습니다.

• 변수를 초기화한 후 조건을 확인하기 위해 while 루프를 생성합니다. 대기열 쌍이 비어 있지 않으면 노드 수가 처음부터 시작됩니다. 다음으로, 최소 합계를 계산하기 위해 트리의 다음 깊이로 이동하므로 'pop()' 메서드를 사용하여 기존 노드를 제거합니다.

• 이제 합계의 최소 합계를 반환하는 세 개의 if 문을 만들어 보겠습니다.

• 이후에는 메인 함수를 시작하고 루트 포인터, 왼쪽 및 오른쪽 하위 노드를 각각 사용하여 입력 모드의 트리 구조를 구축하고 새로운 'tree_node'를 통해 노드 값을 전달합니다.

• 마지막으로 'minimum_sum_at_each_length(root)' 함수를 호출하고 매개변수 루트를 전달하여 각 깊이의 최소 합계를 계산합니다. 다음으로, "비순환 그래프의 각 깊이의 합"이라는 문을 인쇄하고 결과를 얻습니다.

페어 큐는 큐 요소 쌍을 포함하는 컨테이너라는 점을 기억하세요.

Example

의 중국어 번역은

Example

입니다.

이 프로그램에서는 각 깊이에 대한 모든 최소 노드의 합을 계산합니다.

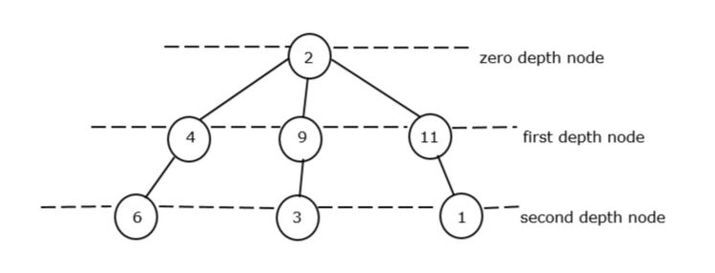
그림 2에서 총 깊이의 최소 합은 15+8+4+1 = 13입니다.

现在我们将把这个数字作为该程序的输入。

#include <iostream>
#include <queue> 

// required for FIFO operation
#include <utility> 

// required for queue pair
#include <climits>
using namespace std;

// create the structure definition for a binary tree node of non-cycle graph
struct tree_node {
   int val;
   tree_node *left;
   tree_node *right;
   tree_node(int x) {
      val = x;
      left = NULL;
      right = NULL;
   }
};
// This function is used to find the minimum sum at each depth
int minimum_sum_at_each_depth(tree_node* root) {
   if (root == NULL) {
      return 0;
   }
   queue<pair<tree_node*, int>> q;
   // create a queue to store node and depth and include pair to combine two together values.
   q.push(make_pair(root, 0)); 
   
   // construct a pair object with two element
   int present_depth = -1; 
   
   // present depth
   int present_sum = 0; 
   
   // present sum for present depth
   int totalSum = 0; 
   
   // Total sum for all depths
   while (!q.empty()) {
      pair<tree_node*, int> present = q.front(); 
      
      // assign queue pair - present
      q.pop();
      
      // delete an existing element from the beginning
      if (present.second != present_depth) {
      
         // We are moving to a new depth, so update the total sum and reset the present sum
         present_depth = present.second;
         totalSum += present_sum;
         present_sum = INT_MAX;
      }

      // Update the present sum with the value of the present node
      present_sum = min(present_sum, present.first->val);
      
      //We are adding left and right children to the queue for updating the new depth.
      if (present.first->left) {
         q.push(make_pair(present.first->left, present.second + 1));
      }
      if (present.first->right) {
         q.push(make_pair(present.first->right, present.second + 1));
      }
   }
   
   // We are adding the present sum of last depth to the total sum
   totalSum += present_sum;
   return totalSum;
}

// start the main function
int main() {
   tree_node *root = new tree_node(15);
   root->left = new tree_node(14);
   root->left->left = new tree_node(11);
   root->left->right = new tree_node(4);
   root->right = new tree_node(8);
   root->right->left = new tree_node(13);
   root->right->right = new tree_node(16);
   root->left->left->left = new tree_node(1);
   root->left->right->left = new tree_node(6);
   root->right->right->right = new tree_node(2);
   root->right->left->right = new tree_node(7);

   cout << "Total sum at each depth of non cycle graph: " << minimum_sum_at_each_depth(root) << endl; 
   return 0;
}

输出

Total sum at each depth of non cycle graph: 28

结论

我们探讨了给定非循环图中每个深度的元素最小和的概念。我们看到箭头运算符连接节点并构建树形结构，利用它计算每个深度的最小和。该应用程序使用非循环图，例如城市规划、网络拓扑、谷歌地图等。

위 내용은 비순환 그래프가 주어지면 각 깊이에서 요소의 최소 합을 계산합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!