주어진 이진 검색 트리에서 더 큰 값을 모두 각 노드에 추가합니다.
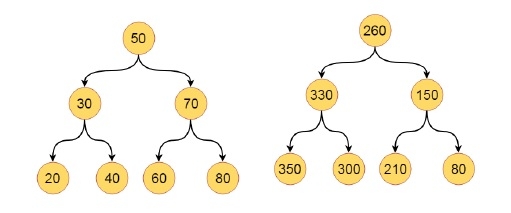
여기서 흥미로운 문제를 볼 수 있습니다. 주어진 이진 검색 트리의 각 노드에 더 큰 값을 추가합니다. 따라서 초기 및 최종 트리는 다음과 같습니다. -
알고리즘
bstUpdate(root, sum) -
Begin if root is null, then stop bstUpdate(right of room, sum) sum := sum + value of root update root value using sum bstUpdate(left of room, sum) End
Example
#include<iostream>
using namespace std;
class Node {
public:
int data;
Node *left, *right;
};
Node *getNode(int item) {
Node *newNode = new Node();
newNode->data = item;
newNode->left = newNode->right = NULL;
return newNode;
}
void updateBST(Node *root, int *sum) {
if (root == NULL)
return;
updateBST(root->right, sum); //update right sub tree
*sum = *sum + root->data;
root->data = *sum; //update root data
updateBST(root->left, sum); //update left sub tree
}
void BSTUpdate(Node *root) {
int sum = 0;
updateBST(root, &sum);
}
void inorder(Node *root) {
if (root != NULL) {
inorder(root->left);
cout<<root->data<<" ";
inorder(root->right);
}
}
Node* insert(Node* node, int data) {
if (node == NULL)
return getNode(data);
if (data <= node->data) //go to left
node->left = insert(node->left, data);
else //go to right
node->right = insert(node->right, data);
return node;
}
int main() {
int data[] = {50, 30, 20, 40, 70, 60, 80};
int n = sizeof(data)/sizeof(data[0]);
Node *root = NULL;
for(int i = 0; i < n; i++) {
root = insert(root, data[i]);
}
BSTUpdate(root);
inorder(root);
}output
350 330 300 260 210 150 80
위 내용은 주어진 이진 검색 트리에서 더 큰 값을 모두 각 노드에 추가합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7700
7700
 15
15
 1640
1640
 14
14
 1393
1393
 52
52
 1287
1287
 25
25
 1230
1230
 29
29
 큐를 사용하여 이진 검색 트리에서 경로를 바꾸는 C++ 코드
Sep 14, 2023 pm 07:21 PM
큐를 사용하여 이진 검색 트리에서 경로를 바꾸는 C++ 코드
Sep 14, 2023 pm 07:21 PM
예를 들어, 이진 검색 트리가 주어지면 특정 키에서 경로를 바꿔야 합니다. 솔루션을 찾는 방법 이 접근 방식에서는 대기열을 생성하고 루트 노드를 얻을 때까지 모든 노드를 푸시합니다. p>예제 #include<bits/stdc++.h>usingnamespacestd;structnode{ intkey structnode*left,*right;};structnode*newNode(intitem){&nb;
 C++의 이진 힙과 이진 검색 트리
Aug 22, 2023 pm 04:10 PM
C++의 이진 힙과 이진 검색 트리
Aug 22, 2023 pm 04:10 PM
C++ 프로그래밍에서 이진 힙과 이진 검색 트리는 일반적으로 사용되는 두 가지 데이터 구조로 유사점이 있지만 차이점도 있습니다. 이 기사에서는 이진 힙 및 이진 검색 트리의 개념, 기본 작업 및 응용 시나리오를 각각 소개합니다. 1. 이진 힙 1.1 개념 이진 힙은 다음 두 가지 속성을 만족하는 완전한 이진 트리입니다. 1.1.1 힙 순서 힙 순서란 이진 힙에서 각 노드의 값이 노드보다 크거나 작지 않다는 것을 의미합니다. 상위 노드의 값입니다. 여기서는 최대 힙을 예로 들어보겠습니다. 즉, 루트 노드의 값은 전체 트리에서 가장 큰 값이며,
 Python에서 이진 검색 트리를 구현하는 방법
Jun 10, 2023 am 08:57 AM
Python에서 이진 검색 트리를 구현하는 방법
Jun 10, 2023 am 08:57 AM
BST(Binary Search Tree)는 이진 트리를 기반으로 하는 검색 알고리즘입니다. 그 특징은 트리에 있는 각 노드의 왼쪽 하위 트리의 값이 이 노드의 값보다 작은 반면, 오른쪽 하위 트리의 값은 이 노드의 값보다 크다는 것입니다. 따라서 BST 검색 및 삽입 연산의 시간복잡도는 O(logN)이다. Python에서 이진 검색 트리를 구현하는 방법은 상대적으로 간단합니다. Python에는 두 개의 내장 데이터 구조인 목록과 사전이 있으며 둘 다 이진 트리를 구현하는 데 사용할 수 있기 때문입니다. 이것에
 Jul 24, 2023 pm 11:17 PM
Jul 24, 2023 pm 11:17 PM
Java는 Math 클래스의 max() 함수를 사용하여 두 숫자의 더 큰 값을 얻습니다. Java 프로그래밍에서는 종종 두 숫자의 크기를 비교한 다음 일부 작업을 수행하기 위해 더 큰 숫자를 선택해야 합니다. Java의 Math 클래스는 수학 연산을 위한 많은 함수를 제공하며, 그 중 max() 함수는 두 숫자의 더 큰 값을 얻는 데 도움이 될 수 있습니다. Math.max() 함수는 다음과 같이 정의됩니다. publicstaticintmax(inta,intb) 이 함수는 두 개의 정수를 허용합니다.
 C#을 사용하여 이진 검색 트리 알고리즘을 작성하는 방법
Sep 19, 2023 pm 01:03 PM
C#을 사용하여 이진 검색 트리 알고리즘을 작성하는 방법
Sep 19, 2023 pm 01:03 PM
C#을 사용하여 이진 검색 트리 알고리즘을 작성하려면 특정 코드 예제가 필요합니다. 이진 검색 트리(BST라고 함)는 빠른 삽입, 검색 및 삭제 작업의 특성을 갖는 일반적으로 사용되는 데이터 구조입니다. C#에서는 개체 지향 접근 방식을 사용하여 이진 검색 트리 알고리즘을 작성할 수 있습니다. 먼저 왼쪽 및 오른쪽 하위 노드에 대한 두 개의 포인터와 값을 포함하는 이진 검색 트리 노드에 대한 클래스를 정의해야 합니다. 코드는 다음과 같습니다: publicclassBST
 Java를 사용하여 이진 검색 트리 알고리즘을 구현하는 방법
Sep 19, 2023 am 08:48 AM
Java를 사용하여 이진 검색 트리 알고리즘을 구현하는 방법
Sep 19, 2023 am 08:48 AM
Java를 사용하여 이진 검색 트리 알고리즘을 구현하는 방법 이진 검색 트리(BinarySearchTree, 줄여서 BST)는 삽입, 삭제, 검색 등의 작업을 효율적으로 구현할 수 있는 일반적으로 사용되는 데이터 구조입니다. 이 기사에서는 Java를 사용하여 이진 검색 트리를 구현하는 방법을 소개하고 해당 코드 예제를 제공합니다. 1. 이진 검색 트리의 정의 이진 검색 트리는 다음과 같은 특성을 갖는 순서 트리입니다. 각 노드는 고유한 키 값을 갖습니다. 왼쪽 하위 트리의 키 값은 노드의 키 값보다 작고, 오른쪽 하위 트리의 키 값은 노드의 키 값보다 큽니다.
 주어진 이진 검색 트리에서 더 큰 값을 모두 각 노드에 추가합니다.
Sep 16, 2023 pm 08:45 PM
주어진 이진 검색 트리에서 더 큰 값을 모두 각 노드에 추가합니다.
Sep 16, 2023 pm 08:45 PM
여기서 우리는 흥미로운 문제를 보게 될 것입니다. 우리는 주어진 이진 검색 트리의 각 노드에 더 큰 값을 추가할 것입니다. 따라서 초기 및 최종 트리는 다음과 같습니다. 알고리즘 bstUpdate(root,sum)-Begin ifrootisnull, thenstop bstUpdate(rightofroom,sum) sum:=sum+valueofroot updaterootvalueus
 주어진 이진 검색 트리에서 더 큰 값을 모두 각 노드에 추가합니다.
Sep 07, 2023 pm 12:17 PM
주어진 이진 검색 트리에서 더 큰 값을 모두 각 노드에 추가합니다.
Sep 07, 2023 pm 12:17 PM
BST(Binary Search Tree)는 왼쪽 노드는 모두 루트 노드 값보다 작은 값을 갖고, 오른쪽 노드는 모두 루트 노드 값보다 큰 값을 갖는 이진 트리 형태이다. 이 문제에서는 이진 트리를 가져와 현재 노드 값보다 큰 모든 값을 추가합니다. "BST의 각 노드에 더 큰 값을 모두 추가"하는 문제는 BST의 경우 현재 노드 값보다 큰 모든 노드 값을 해당 노드 값에 추가하는 것으로 단순화됩니다. BST 문제 설명의 각 노드에 더 큰 값의 노드를 모두 추가합니다. BST(이진 검색 트리)가 주어지면 각 노드에 더 큰 값의 모든 노드의 합계를 추가해야 합니다. 10을 입력하세요.




