Floyd-Warshal 알고리즘을 사용하여 두 노드 사이의 최단 경로를 찾습니다.
C++에는 코드 조각이나 예상 값으로 정의되는 매크로가 있으며 사용자가 필요할 때마다 재사용됩니다. Floyd-Walshall 알고리즘은 주어진 가중치 그래프에서 모든 정점 쌍 사이의 최단 경로를 찾는 프로세스입니다. 알고리즘은 최소 가중치 그래프를 찾기 위해 동적 프로그래밍 접근 방식을 따릅니다.
프로이트-월셔 알고리즘의 의미를 다이어그램을 통해 이해해 봅시다 -
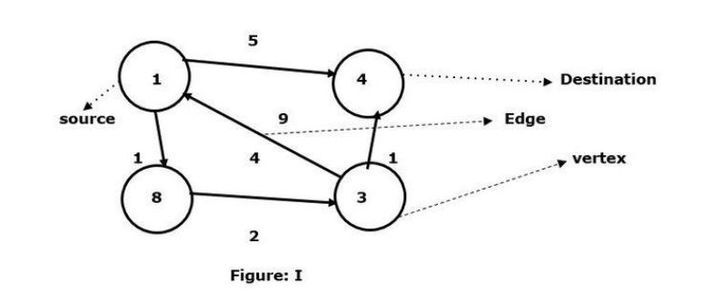
꼭지점 1을 소스로 하고 꼭지점 4을 목적지로 하여 둘 사이의 최단 경로를 찾습니다.
대상 정점 4에 연결될 수 있는 경로가 두 개 있다는 것을 확인했습니다.
1 -> 4 – 가장자리의 무게는 5
1 -> 8 -> 3 -> 4 – 가장자리 가중치(1+2+1)는 4입니다.
주어진 그래프 I에서 두 꼭지점을 연결하는 최소 모서리를 볼 수 있습니다. 따라서 정점 8에서 정점 3까지의 경로는 정점 1을 정점 4으로 연결하고 가장자리는 4입니다. 반면에 정점 1에서 정점 4까지 방향이 있는 가장자리가 있고 가장자리의 가중치는 5입니다.
이제 4과 5이라는 두 가지 가중치를 비교합니다. 따라서 여기서 4는 Floyd Warshall 알고리즘에 따라 계산된 그래프의 최소 가중치입니다.
이 기사에서는 Floyd Warshall 알고리즘을 사용하여 주어진 두 노드 사이의 최단 경로를 찾습니다.
문법
다음 구문은 프로그램에서 사용됩니다 -
으아악매개변수
data_type[][] - 사용자가 언급한 데이터 유형입니다. 첫 번째 배열은 행을 나타내고 두 번째 배열은 열을 나타냅니다. 따라서 이는 2차원 배열을 나타냅니다.
array_name - 배열에 지정된 이름입니다.
알고리즘
헤더 파일 'iostream'으로 프로그램을 시작하고 매크로 위치를 'INF'(무한대)로 정의합니다. 나중에 2D 배열 행렬과 if-else 문을 만족하게 되기 때문입니다.
다음으로 'printPath'라는 전역 함수 정의를 만들고 'parent[]', 'i' 및 'j'라는 세 가지 매개 변수를 허용하여 경로가 존재하는지 확인합니다.
그런 다음 주 함수를 시작하고 '4' 값을 정점 수를 나타내는 변수 'V'에 저장합니다. 둘째, 인접 행렬 형태로 값을 변수 'dist[V][V]'에 저장합니다. 우리가 알고 있듯이 dist[i][j]는 인접 행렬을 저장하여 'i'에서 'j'까지의 가장자리 가중치를 정의하는 2D 행렬을 나타냅니다.
다음으로 변수 'parent'에 대한 2D 배열을 크기 [V][V]로 초기화합니다.
두 개의 중첩된 for 루프를 사용하여 최단 경로를 찾을 수 있습니다. 첫 번째 for 루프는 행렬의 행을 반복합니다. 그런 다음 두 번째 for 루프를 통해 행렬의 열을 반복한 후 if-else 문을 사용하여 다음 조건을 확인합니다. -
-
If (dist[i][j] != INF && i != j) { parent[i][j] = i;}
의 중국어 번역은 다음과 같습니다. parent[i][j] = i;}if 문에서 'and' (&&) 연산자를 사용하여 두 조건이 모두 충족되면 'i'가 'parent[i][j]'에 저장되어 다음을 확인합니다. 경로가 존재합니다.
-
기타{ parent[i][j] = -1;}
의 중국어 번역은 다음과 같습니다. parent[i][j] = -1;}else 문에서는 "-1"을 "parent[i][j]"로 초기화하여 경로가 존재하지 않는지 확인합니다.
이제 3개의 중첩된 for 루프로 시작하고 0에서 V-1 사이의 범위에 k개의 정점을 적용합니다. 이 범위의 도움으로 최단 거리와 경로가 업데이트됩니다. 세 번째 중첩 루프에서는
이 변수에서 우리는 정점 'i' 및 'j' w.r.t 'parent[i][j]'.
의 각 쌍을 표시하는 데 사용합니다.다음으로 다음 조건을 제공하여 모든 정점 쌍의 최단 거리와 경로를 인쇄합니다
두 개의 중첩된 for 루프를 사용하여 최단 거리와 경로를 인쇄합니다.
두 번째 for 루프 아래의 if 문을 사용하여 dist[i][j]가 무한대인지 확인합니다. 무한대인 것으로 확인되면 "INF"를 인쇄하고, 그렇지 않으면 최단 경로를 인쇄합니다.
마지막으로 세 개의 매개변수(parent[i], i, j)를 전달하여 'printPath()'라는 함수를 호출합니다.
여기서 K는 새로 업데이트된 최단 경로와 거리를 확인하는 2D 배열 행렬의 행과 열 부분을 업데이트하고 있습니다.
예
이 프로그램에서는 Floyd Warshall 알고리즘을 사용하여 두 노드 사이의 최단 경로를 계산합니다.
#include <iostream>
using namespace std;
#define INF 1000000000 // Infinity
void printPath(int parent[], int i, int j) {
if (i == j)
cout << i << " ";
else if (parent[j] == -1)
cout << "No path exists";
else
{
printPath(parent, i, parent[j]);
cout << j << " ";
}
}
int main()
{
int V = 4;
// V represent number of vertices
int dist[V][V] = {{0, 2, INF, 4},
{6, 0, 5, 3},
{INF, 10, 0, 1},
{7, 9, 8, 0}};
// Represent the graph using adjacency matrix
// Apply the Floyd Warshall algorithm to find the shortest paths
int parent[V][V];
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
if (dist[i][j] != INF && i != j)
parent[i][j] = i;
else
parent[i][j] = -1;
}
}
// update the path and distance using the k vertex range from 0 to V-1.
for (int k = 0; k < V; k++)
{
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
if (dist[i][j] > dist[i][k] + dist[k][j])
{
dist[i][j] = dist[i][k] + dist[k][j];
parent[i][j] = parent[k][j];
}
}
}
}
// Print shortest distances and paths between all pairs of vertices
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
cout << "The Shortest distance between " << i << " and " << j << " is ";
if (dist[i][j] == INF)
cout << "INF ";
else
cout << dist[i][j] << " ";
cout << "and the shortest path is:- ";
printPath(parent[i], i, j);
cout << endl;
}
}
return 0;
}
输出
The Shortest distance between 0 and 0 is 0 and the shortest path is:- 0 The Shortest distance between 0 and 1 is 2 and the shortest path is:- 0 1 The Shortest distance between 0 and 2 is 7 and the shortest path is:- 0 1 2 The Shortest distance between 0 and 3 is 4 and the shortest path is:- 0 3 The Shortest distance between 1 and 0 is 6 and the shortest path is:- 1 0 The Shortest distance between 1 and 1 is 0 and the shortest path is:- 1 The Shortest distance between 1 and 2 is 5 and the shortest path is:- 1 2 The Shortest distance between 1 and 3 is 3 and the shortest path is:- 1 3 The Shortest distance between 2 and 0 is 8 and the shortest path is:- 2 3 0 The Shortest distance between 2 and 1 is 10 and the shortest path is:- 2 1 The Shortest distance between 2 and 2 is 0 and the shortest path is:- 2 The Shortest distance between 2 and 3 is 1 and the shortest path is:- 2 3 The Shortest distance between 3 and 0 is 7 and the shortest path is:- 3 0 The Shortest distance between 3 and 1 is 9 and the shortest path is:- 3 1 The Shortest distance between 3 and 2 is 8 and the shortest path is:- 3 2 The Shortest distance between 3 and 3 is 0 and the shortest path is:- 3
结论
我们学习了使用Floyd Warshall算法找到任意两个节点之间的最短路径的概念。我们使用邻接矩阵作为程序的输入,通过它我们找到了最短路径和距离。此外,为了更新路径和距离,我们使用了k个顶点来更新行和列。在我们的日常生活中,我们在谷歌地图上搜索最短路线或路径,从一个起点到目的地。
위 내용은 Floyd-Warshal 알고리즘을 사용하여 두 노드 사이의 최단 경로를 찾습니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7540
7540
 15
15
 1380
1380
 52
52
 83
83
 11
11
 55
55
 19
19
 21
21
 86
86
 트리에 있는 모든 최단 경로 쌍의 합
Aug 28, 2023 pm 03:17 PM
트리에 있는 모든 최단 경로 쌍의 합
Aug 28, 2023 pm 03:17 PM
트리에서 "모든 노드 쌍의 최단 경로의 합"이라는 용어는 모든 노드 쌍의 개별 최단 경로의 합을 계산하는 것을 의미합니다. 효과적인 방법은 이중 DFS(깊이 우선 탐색) 알고리즘을 사용하는 것입니다. 선택한 노드와 다른 모든 노드 사이의 거리는 첫 번째 DFS 순회 중에 결정됩니다. 두 번째 DFS 패스 동안 트리를 다시 탐색하여 각 노드를 잠재적인 LCA(최저 공통 조상)로 간주하고 선택한 LCA의 하위 노드 쌍 사이의 거리 합계를 계산합니다. 이 방법을 사용하면 트리의 모든 노드 쌍에 대한 최단 경로의 합을 계산하고 이상적인 솔루션을 보장할 수 있습니다. 사용된 방법 이중 DFS(깊이 우선 검색) 방법 동적 프로그래밍 방법 트리에 대한 이중 DFS(깊이 우선 검색) 방법 모든 최단 경로 쌍
 노드 X에서 시작하여 하위 트리의 최소 가중치와 최대 D의 거리를 쿼리합니다.
Aug 25, 2023 am 11:25 AM
노드 X에서 시작하여 하위 트리의 최소 가중치와 최대 D의 거리를 쿼리합니다.
Aug 25, 2023 am 11:25 AM
컴퓨터 프로그래밍을 할 때 특정 노드에서 시작되는 하위 트리의 최소 가중치를 찾아야 하는 경우가 있습니다. 단, 해당 하위 트리에는 지정된 노드에서 D 단위 이상 떨어진 노드가 포함될 수 없습니다. 이 문제는 그래프 이론, 트리 기반 알고리즘, 네트워크 최적화 등 다양한 분야와 응용 분야에서 발생합니다. 하위 트리는 더 큰 트리 구조의 하위 집합으로, 지정된 노드가 하위 트리의 루트 노드 역할을 합니다. 하위 트리에는 루트 노드의 모든 자손과 해당 연결 가장자리가 포함됩니다. 노드의 가중치는 해당 노드에 할당된 특정 값을 나타내며, 이는 중요도, 중요도 또는 기타 관련 측정항목을 나타낼 수 있습니다. 이 문제의 목표는 루트 노드에서 최대 D 단위 떨어진 노드로 하위 트리를 제한하면서 하위 트리의 모든 노드 중에서 최소 가중치를 찾는 것입니다. 다음 기사에서는 하위 트리에서 최소 가중치를 마이닝하는 복잡성에 대해 자세히 살펴보겠습니다.
 Vue와 jsmind를 통해 마인드맵의 노드 복사 및 잘라내기 기능을 구현하는 방법은 무엇입니까?
Aug 15, 2023 pm 05:57 PM
Vue와 jsmind를 통해 마인드맵의 노드 복사 및 잘라내기 기능을 구현하는 방법은 무엇입니까?
Aug 15, 2023 pm 05:57 PM
Vue와 jsmind를 통해 마인드맵의 노드 복사 및 잘라내기 기능을 구현하는 방법은 무엇입니까? 마인드맵은 우리의 생각을 정리하고 사고 논리를 정리하는 데 도움이 되는 일반적인 사고 도구입니다. 노드 복사 및 잘라내기 기능은 마인드맵에서 흔히 사용되는 작업으로, 기존 노드를 보다 편리하게 재사용하고 사고 정리의 효율성을 높일 수 있습니다. 이 글에서는 Vue와 jsmind라는 두 가지 도구를 사용하여 마인드맵의 노드 복사 및 잘라내기 기능을 구현해 보겠습니다. 먼저 Vue와 jsmind를 설치하고 생성해야 합니다.
 Java를 사용하여 최단 경로 알고리즘을 구현하는 방법
Sep 19, 2023 am 08:18 AM
Java를 사용하여 최단 경로 알고리즘을 구현하는 방법
Sep 19, 2023 am 08:18 AM
최단 경로 알고리즘을 구현하기 위해 Java를 사용하는 방법 개요: 최단 경로 알고리즘은 그래프 이론의 중요한 응용 프로그램이며 네트워크 라우팅, 지도 탐색 및 기타 분야에서 널리 사용됩니다. 이번 글에서는 Java를 이용하여 최단 경로 알고리즘을 구현하는 방법을 알아보고 구체적인 코드 예제를 제공하겠습니다. 알고리즘 아이디어: 최단 경로 알고리즘을 구현하는 방법에는 여러 가지가 있으며 그 중 가장 유명한 두 가지 알고리즘은 Dijkstra 알고리즘과 A* 알고리즘입니다. 여기서는 Dijkstra 알고리즘의 구현에 중점을 둘 것입니다. Dijkstra 알고리즘의 기초
 js에서 노드를 삭제하는 방법은 무엇입니까
Sep 01, 2023 pm 05:00 PM
js에서 노드를 삭제하는 방법은 무엇입니까
Sep 01, 2023 pm 05:00 PM
js에서 노드를 삭제하는 방법은 다음과 같습니다. 1. RemoveChild() 메서드는 부모 노드에서 지정된 자식 노드를 제거하는 데 사용됩니다. 첫 번째 매개 변수는 삭제할 자식 노드이고 두 번째 매개 변수는 다음과 같습니다. 2. parentNode.removeChild() 메소드는 하위 노드를 삭제하기 위해 상위 노드를 통해 직접 호출될 수 있습니다. 3. Remove() 메소드는 상위 노드를 지정하지 않고 노드를 직접 삭제할 수 있습니다. innerHTML 속성은 노드 내용을 삭제하는 데 사용됩니다.
 Floyd-Warshal 알고리즘을 사용하여 두 노드 사이의 최단 경로를 찾습니다.
Sep 20, 2023 pm 02:21 PM
Floyd-Warshal 알고리즘을 사용하여 두 노드 사이의 최단 경로를 찾습니다.
Sep 20, 2023 pm 02:21 PM
C++에는 코드 조각이나 예상 값으로 정의되는 매크로가 있으며 사용자가 필요할 때마다 재사용됩니다. Floyd-Walshall 알고리즘은 주어진 가중치 그래프에서 모든 정점 쌍 사이의 최단 경로를 찾는 프로세스입니다. 알고리즘은 최소 가중치 그래프를 찾기 위해 동적 프로그래밍 접근 방식을 따릅니다. Floyd-Walshall 알고리즘의 의미를 다이어그램을 통해 이해해 봅시다. 정점 1을 소스로 하고 정점 4를 목적지로 삼아 이들 사이의 최단 경로를 찾습니다. 우리는 대상 정점 4에 연결될 수 있는 두 개의 경로가 있음을 확인했습니다. 1->4 – 가장자리의 가중치는 51->8->3->4 – 가장자리의 가중치(1+2+1) 4입니다. 주어진 그래프 I에서 두 꼭지점을 연결하는 가장 작은 가장자리를 볼 수 있습니다. 그래서 여기 꼭지점
 js에서 요소 노드를 생성, 삭제, 추가 및 교체하는 방법(코드 예제 포함)
Aug 06, 2022 pm 05:26 PM
js에서 요소 노드를 생성, 삭제, 추가 및 교체하는 방법(코드 예제 포함)
Aug 06, 2022 pm 05:26 PM
이번 글은 주로 js에서 요소 노드를 생성, 삭제, 추가, 교체하는 방법을 소개합니다. 도움이 필요한 친구들에게 도움이 되었으면 좋겠습니다!
 주어진 그래프에서 두 노드 사이의 경로가 최단 경로를 나타내는지 확인합니다.
Sep 07, 2023 pm 06:57 PM
주어진 그래프에서 두 노드 사이의 경로가 최단 경로를 나타내는지 확인합니다.
Sep 07, 2023 pm 06:57 PM
그래프의 두 중심 사이의 주어진 경로가 최단 경로를 따르는지 확인하려면 다음과 같은 신뢰할 수 있는 최단 경로를 사용하여 주어진 경로를 따른 전체 간선 가중치를 동일한 중심 조합 간의 최단 거리와 비교하여 계산할 수 있습니다. Dijkstra의 계산 또는 Floyd-Warshall 계산. 주어진 경로의 모든 간선 가중치가 가장 제한된 삭제와 일치하면 이는 가장 간단한 경로를 나타냅니다. 또한: 전체 모서리 가중치가 최단 거리보다 더 두드러지면 그래프에서 두 중심 사이의 거리가 짧다는 것을 나타냅니다. 사용된 방법 Dijkstra 알고리즘 Floyd-Warshall 알고리즘 한계 반전 비용 탐욕 알고리즘 Dijkstra 계산은 널리 사용되는 그래프 순회 계산일 수 있습니다.




