가우스 혼합 모델을 사용하여 다중 모드 분포 분해-일체 포함-php.cn

가우스 혼합 모델을 사용하여 다중 모드 분포 분해

WBOY

풀어 주다： 2023-09-30 11:09:16

앞으로

1956명이 탐색했습니다.

1차원 다중 모드 분포는 Gaussian Mixture Model을 사용하여 여러 분포로 분할할 수 있습니다.

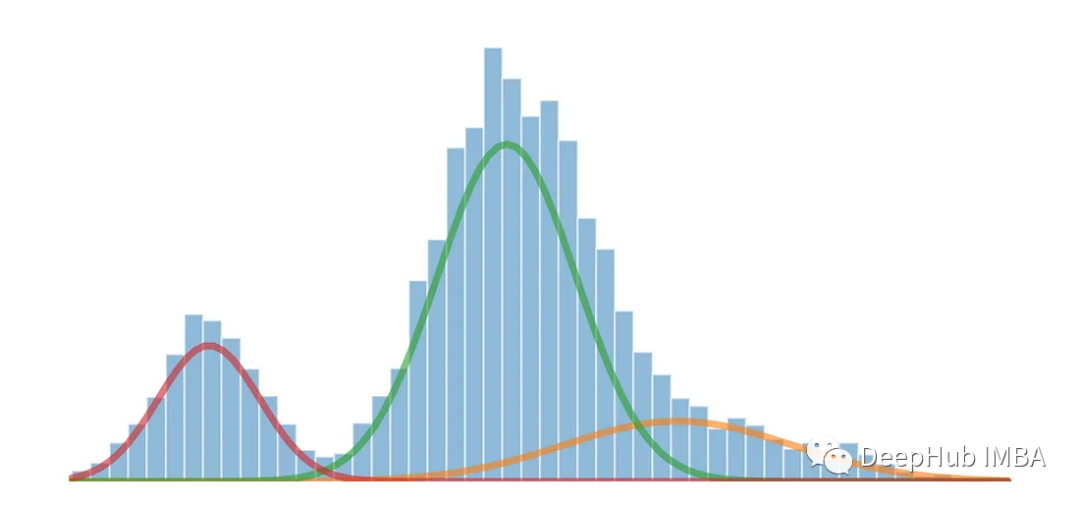
가우스 혼합 모델을 사용하여 다중 모드 분포 분해

Gaussian Mixture Models(GMM)은 통계 및 기계 학습 분야에서 일반적으로 사용되는 방법입니다. 복잡한 데이터 분포를 분석합니다. GMM은 관측된 데이터가 여러 개의 가우스 분포로 구성되어 있다고 가정하고 각 가우스 분포를 구성 요소라고 하며 이러한 구성 요소는 가중치를 통해 데이터에 대한 기여도를 제어한다고 가정하는 생성 모델입니다.

다중 모드 분포를 사용하여 데이터 생성

데이터 세트에 여러 개의 서로 다른 피크 또는 모드가 표시되는 경우 이는 일반적으로 데이터 세트에 여러 개의 눈에 띄는 클러스터 또는 데이터 포인트 집중이 있음을 의미합니다. 각 모드는 분포에서 데이터 포인트의 눈에 띄는 클러스터 또는 집중을 나타내며 데이터 값이 발생할 가능성이 더 높은 고밀도 영역으로 생각할 수 있습니다

우리는 numpy로 생성된 1차원 배열을 사용합니다 .

import numpy as np  dist_1 = np.random.normal(10, 3, 1000) dist_2 = np.random.normal(30, 5, 4000) dist_3 = np.random.normal(45, 6, 500)  multimodal_dist = np.concatenate((dist_1, dist_2, dist_3), axis=0)

로그인 후 복사

1차원 데이터 분포를 시각화해 보겠습니다.

import matplotlib.pyplot as plt import seaborn as sns sns.set_style('whitegrid')  plt.hist(multimodal_dist, bins=50, alpha=0.5) plt.show()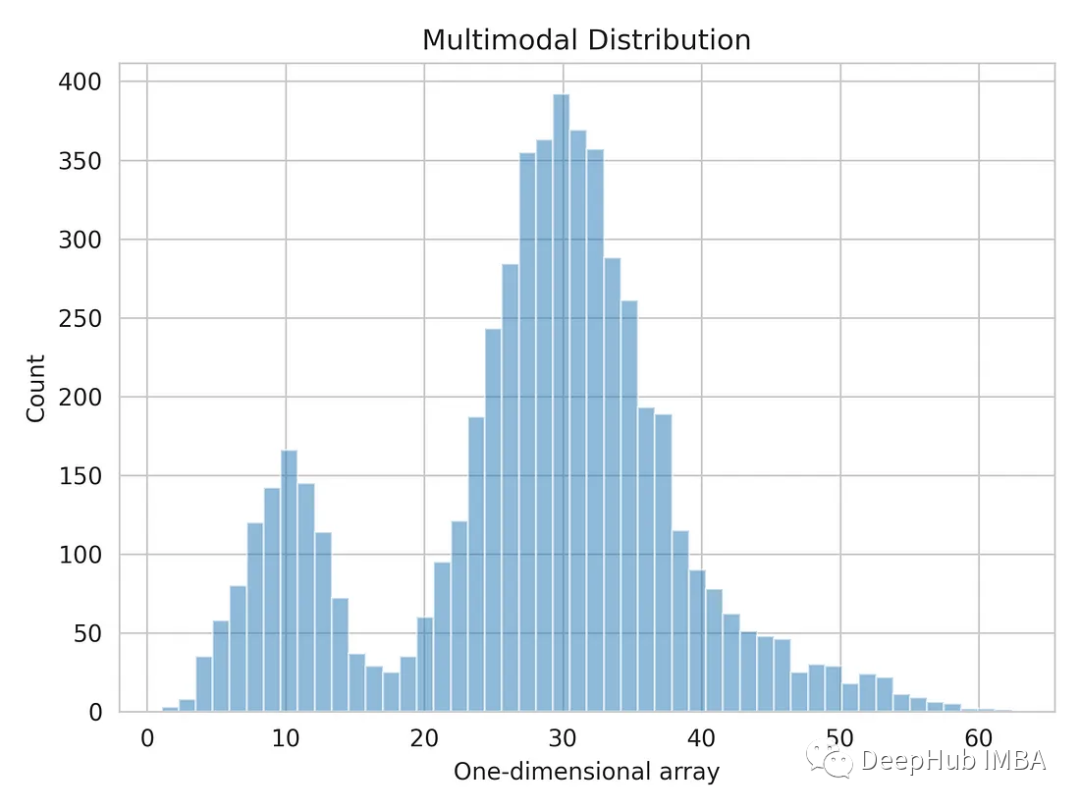

로그인 후 복사

가우스 혼합 모델을 사용하여 다중 모드 분포 분해

Gaussian 혼합 모델을 사용하여 다중 모드 분포 분할

가우시안 혼합 모델을 사용하여 각 분포의 평균과 표준 편차를 계산하여 다중 모드 분포를 3개의 원래 분포로 분리합니다. 가우스 혼합 모델은 데이터 클러스터링에 사용할 수 있는 비지도 확률 모델입니다. 기대값 최대화 알고리즘을 사용하여 밀도 영역을 추정합니다.

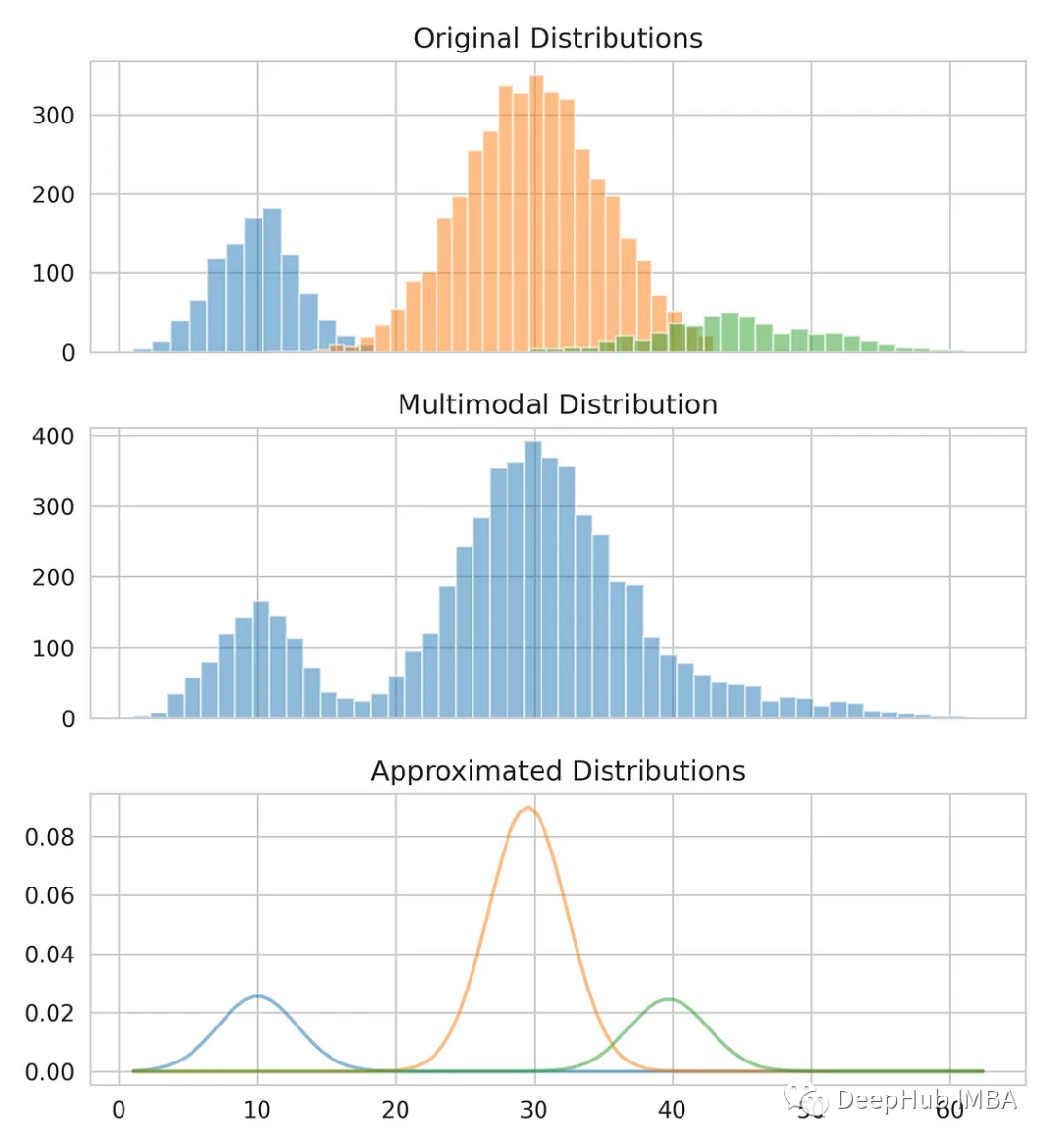
from sklearn.mixture import GaussianMixture  gmm = GaussianMixture(n_compnotallow=3) gmm.fit(multimodal_dist.reshape(-1, 1))  means = gmm.means_  # Conver covariance into Standard Deviation standard_deviations = gmm.covariances_**0.5  # Useful when plotting the distributions later weights = gmm.weights_   print(f"Means: {means}, Standard Deviations: {standard_deviations}")  #Means: [29.4, 10.0, 38.9], Standard Deviations: [4.6, 3.1, 7.9]

로그인 후 복사

원래 분포를 모델링하기 위한 평균과 표준 편차가 이미 있습니다. 평균과 표준편차가 정확하게 정확하지 않을 수도 있지만 대략적인 추정치를 제공한다는 것을 알 수 있습니다.

저희 추정치를 원본 데이터와 비교해 보세요.

from scipy.stats import norm  fig, axes = plt.subplots(nrows=3, ncols=1, sharex='col', figsize=(6.4, 7))  for bins, dist in zip([14, 34, 26], [dist_1, dist_2, dist_3]):axes[0].hist(dist, bins=bins, alpha=0.5)  axes[1].hist(multimodal_dist, bins=50, alpha=0.5)  x = np.linspace(min(multimodal_dist), max(multimodal_dist), 100)  for mean, covariance, weight in zip(means, standard_deviations, weights):pdf = weight*norm.pdf(x, mean, std)plt.plot(x.reshape(-1, 1), pdf.reshape(-1, 1), alpha=0.5)  plt.show()

로그인 후 복사

가우스 혼합 모델을 사용하여 다중 모드 분포 분해