테렌스 타오(Terence Tao)가 또 다른 60년 기하학 문제에 접근합니다! 주기적인 밀착 포장 문제에 새로운 돌파구가 마련되었습니다.
Tao Zhexuan은 주기 타일링 문제 연구에 새로운 돌파구를 마련했습니다
9월 18일 Tao Zhexuan과 Rachel Greenfeld는 사전 인쇄 논문 "Undecidability of Translational Monotilings"를 arXiv에 업로드했습니다.

문서 주소: https://arxiv.org/abs/2309.09504
이 논문의 주요 결론은 그리드의 차원이 무한하다면 그리드의 유한 분할을 결정한다는 것입니다. 집합이 그리드의 주기적인 부분 집합을 타일링할 수 있는지 여부에 대한 질문은 결정 불가능합니다
이 문제는 차원 1과 차원 2에서 결정 가능합니다.
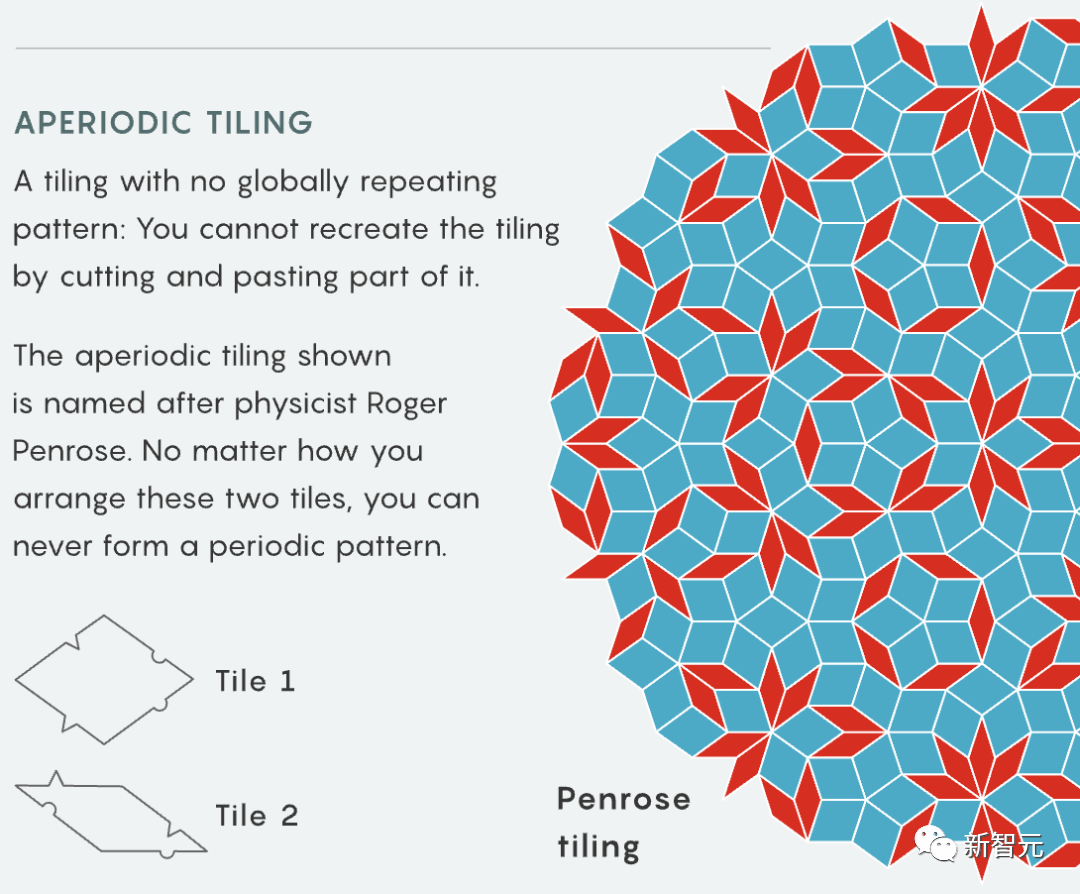
Tao Zhexuan은 기사에서 시연된 대부분의 구성 요소가 인기 게임과 유사하다는 것이 조금 이상하다고 말했습니다.
도미노의 타일 유사품, 스도쿠, 컴퓨터 게임 "테트리스" " , 어린이용 게임 '피즈 버즈'까지 등장
수학 문제를 공부하는데 왜 이렇게 많은 게임이 필요한 걸까요? Tao Zhexuan 또한 병진 단일 조밀 타일링의 결정불가능성을 설명할 수 없습니다. 이 논문은 두 사람의 이전 논문의 후속편입니다. 링크 주기 타일 문제

마지막 논문에서 그들은 고차원 그리드의 병진 단일 조밀 타일링
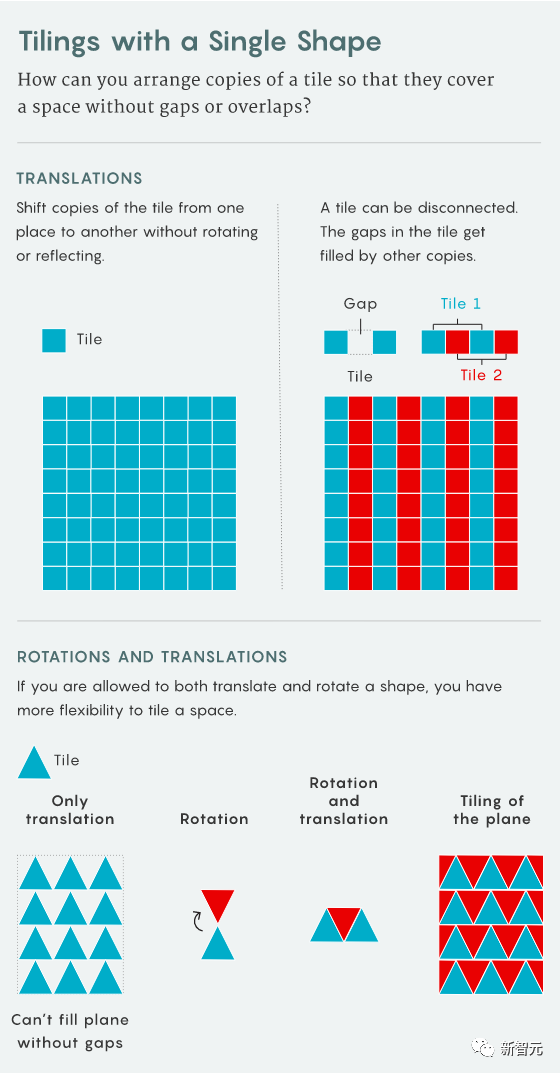
을 구성했습니다(그래서 단일 조밀 타일링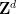 은 유한 집합), 비주기적입니다(이 타일링을 주기적인 타일링
은 유한 집합), 비주기적입니다(이 타일링을 주기적인 타일링 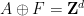 으로 "수정"할 수 있는 방법이 없습니다. 여기서
으로 "수정"할 수 있는 방법이 없습니다. 여기서
에 대해 주기적입니다). 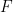
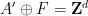
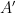 이 사실은 비주기적 조밀하게 포장된 단량체가 존재하지 않는다는 Stein, Grunbaum-Shephard 및 Lagarias-Wang의 가설을 부정합니다.
이 사실은 비주기적 조밀하게 포장된 단량체가 존재하지 않는다는 Stein, Grunbaum-Shephard 및 Lagarias-Wang의 가설을 부정합니다. 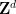 ("Hat Single Densely Packed"는 최근 발견된 비주기적 등각 투영 단일체입니다. 회전, 반사 및 이동이 허용되는 촘촘한 타일링
("Hat Single Densely Packed"는 최근 발견된 비주기적 등각 투영 단일체입니다. 회전, 반사 및 이동이 허용되는 촘촘한 타일링
또는 업데이트된 "고스트 모놀리스" 위의 모놀리스는 반사가 필요하지 않다는 점을 제외하면 모자 단일 촘촘한 타일링과 유사합니다. 
Tao Zhexuan과 Rachel Greenfeld가 이 추측에 영감을 준 이유 중 하나는 수학자 Hao Wang의 관찰입니다.
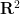 그는 주기적 타일링 추측이 참이라면 병진 타일링 문제가 알고리즘적으로 결정 가능하다는 것을 발견했습니다. ——
그는 주기적 타일링 추측이 참이라면 병진 타일링 문제가 알고리즘적으로 결정 가능하다는 것을 발견했습니다. ——
튜링 기계가 있습니다. 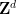 에 대해 차원
에 대해 차원 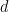 과 유한 부분집합
과 유한 부분집합 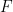 이 주어지면
이 주어지면 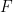 이 테셀레이션될 수 있는지
이 테셀레이션될 수 있는지 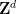 가 제한된 시간 내에 결정될 수 있습니다.
가 제한된 시간 내에 결정될 수 있습니다.
주기적인 타일링이 있으면 컴퓨터 검색을 통해 찾을 수 있기 때문입니다.
타일링이 전혀 없으면 압축 정리를 통해 유한한 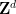 서브가 있음을 알 수 있습니다. 집합, 이러한 하위 집합은
서브가 있음을 알 수 있습니다. 집합, 이러한 하위 집합은 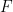 분리된 번역으로 처리할 수 없으며 컴퓨터 검색으로도 찾을 수 있습니다.
분리된 번역으로 처리할 수 없으며 컴퓨터 검색으로도 찾을 수 있습니다.
주기적 테셀레이션 추측은 이것이 유일한 두 가지 가능한 상황임을 주장하여 결정 가능성을 제공합니다.

반면에 Wang의 관점은 불변입니다. 주기적 테셀레이션 추측의 실패가 다른 알고리즘의 존재를 배제하지 않기 때문에 자동으로 변환 단일 테셀레이션 문제의 결정 불가능성을 의미하지는 않습니다. 테셀레이션을 결정하면 이 테셀레이션은 주기적인 테셀레이션의 존재와 무관할 수 있습니다
(예를 들어 새로 발견된 모자와 고스트 테셀레이션의 경우에도 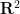 에서 유리수 계수를 갖는 다각형의 등각 단순 단면에 대해 열려 있는 상태로 유지됩니다. 조밀한 타일링 문제가 반사 여부에 따라 결정 가능한지 여부에 대한 질문입니다.
에서 유리수 계수를 갖는 다각형의 등각 단순 단면에 대해 열려 있는 상태로 유지됩니다. 조밀한 타일링 문제가 반사 여부에 따라 결정 가능한지 여부에 대한 질문입니다.
이 문서의 주요 결과는 이 문제를 다루고 있습니다(주의 사항 있음). 정리 1 ere에 대한 알고리즘은 없으며,주기적인 서브 세트
및 유한 서브 세트 
가 주어지면 내부에 패닝 가 있는지 여부를 결정할 수 있습니다. 제한된 시간
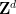 .
.
모두 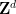 보다는
보다는 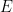 의 주기적 하위 집합
의 주기적 하위 집합 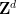 을 사용해야 한다는 점에 유의하는 것이 중요합니다. 이는 주로 이 접근 방식의 기술적 한계로 인한 것이며 추가 노력과 창의성을 통해 달성될 가능성이 높습니다. 제거하기.
을 사용해야 한다는 점에 유의하는 것이 중요합니다. 이는 주로 이 접근 방식의 기술적 한계로 인한 것이며 추가 노력과 창의성을 통해 달성될 가능성이 높습니다. 제거하기.
또한 Terence Tao와 Rachel Greenfeld도 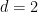 때 Bhattacharya에 의해 주기적인 포장 추측이 확립되었으므로 이 경우 문제는 결정 가능하다는 사실을 알아차렸습니다
때 Bhattacharya에 의해 주기적인 포장 추측이 확립되었으므로 이 경우 문제는 결정 가능하다는 사실을 알아차렸습니다 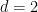 .
.
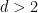 의 고정된 값에 대해 타일링 문제가 결정 가능한지 여부는 여전히 열려 있습니다(위 결과에서 차원
의 고정된 값에 대해 타일링 문제가 결정 가능한지 여부는 여전히 열려 있습니다(위 결과에서 차원 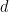 은 고정되지 않고 입력의 일부입니다).
은 고정되지 않고 입력의 일부입니다).
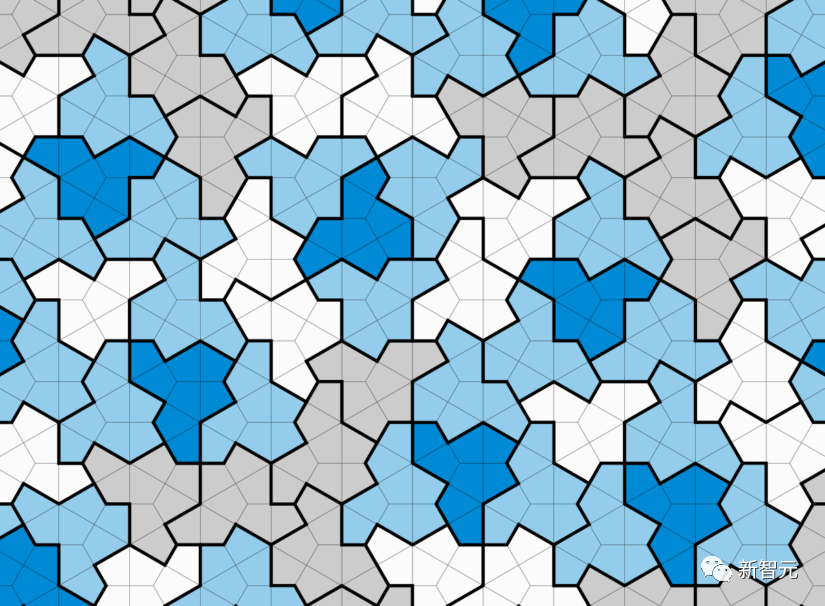
알고리즘 결정 불가능성과 논리적 결정 불가능성(논리적 독립성이라고도 함) 사이의 잘 알려진 연결로 인해 이 정리는 (원칙적으로 명확하게 설명할 수 있는) 차원의 존재를 암시합니다. of 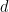 ,
, 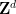 및
및 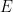 의 유한 부분 집합
의 유한 부분 집합 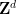 은
은 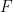 이 번역 타일링
이 번역 타일링 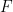 을 통과하도록 하며 ZFC 집합 이론에서 확인되거나 위조될 수 없습니다(물론 이론이 일관성이 있다고 가정). .
을 통과하도록 하며 ZFC 집합 이론에서 확인되거나 위조될 수 없습니다(물론 이론이 일관성이 있다고 가정). . 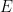 이 접근 방식의 결과로 여기에서
이 접근 방식의 결과로 여기에서
를 "거의 2차원" 그룹  으로 대체할 수도 있습니다. 여기서
으로 대체할 수도 있습니다. 여기서 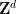 는 유한 아벨 그룹입니다(이제 입력의 일부, 대신 Dimensions
는 유한 아벨 그룹입니다(이제 입력의 일부, 대신 Dimensions 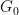 ).
). 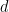 다음으로, 증명의 주요 아이디어 몇 가지를 설명하세요.
다음으로, 증명의 주요 아이디어 몇 가지를 설명하세요.
문제가 결정 불가능하다는 것을 증명하는 일반적인 방법은 결정 불가능하다고 알려진 다른 문제를 원래 문제로 "인코딩"하여 원래 문제를 결정하는 알고리즘이 내장된 문제도 결정할 수 있도록 하는 것입니다
따라서 우리는 Wang Dense Shop 문제를 단일 Density Shop 문제로 인코딩합니다. 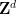 :
:

두 번째 문제는 Wang Dense Shop 문제에 관한 것입니다
타일 세트 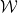 (단위 정사각형, 각 모서리에는 제한된 팔레트의 특정 색상이 할당됨), 인접한 타일이 공통 타일에서 동일한 색상을 갖도록 번역하여 표준 그리드
(단위 정사각형, 각 모서리에는 제한된 팔레트의 특정 색상이 할당됨), 인접한 타일이 공통 타일에서 동일한 색상을 갖도록 번역하여 표준 그리드 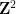 를 사용하여 평면을 테셀레이션하는 것이 가능합니까? 가장자리?
를 사용하여 평면을 테셀레이션하는 것이 가능합니까? 가장자리?
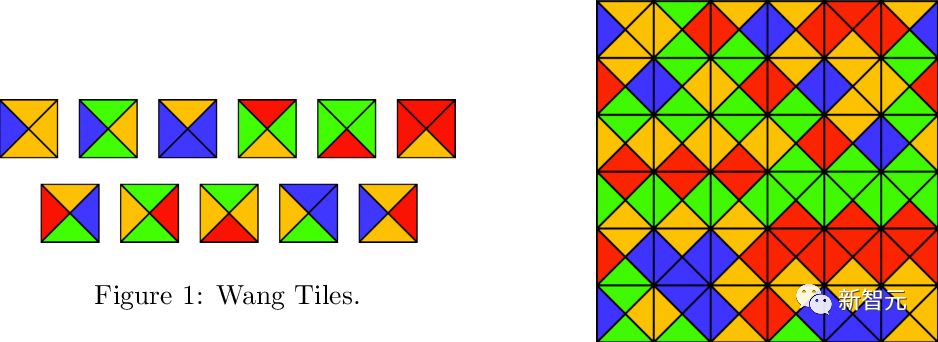
Berger는 이 질문을 결정할 수 없다는 유명한 결론을 내린 적이 있습니다.

다시 작성해야 할 내용은 Berger, Robert입니다.
이 질문을 상위 수준으로 변환하세요. 질문 차원 변환 단일 조밀 타일링 문제는 일부 중간 문제를 해결해야 합니다
우선, 우리는 Wang의 조밀 타일링 문제를 비슷한 문제, 즉 도미노 문제라고 부르는 문제에 쉽게 포함시킬 수 있습니다.

다음과 같이 다시 작성됨: 도미노 문제는 문제 3입니다.
한 쌍의 인접한 셀인 수평(또는 수직) 도미노 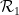 또는
또는 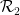 의 유한 집합이 주어지면 정사각형, 각 단위 정사각형은 다음과 같습니다. 유한 집합의 요소 점으로 장식
의 유한 집합이 주어지면 정사각형, 각 단위 정사각형은 다음과 같습니다. 유한 집합의 요소 점으로 장식 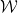 표준 격자 타일
표준 격자 타일 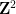 의 각 단위 사각형에 점을 할당하여 이 타일의 각 쌍이 수평(또는 수직) 사각형에서 도미노를 사용할 수 있도록 할 수 있습니까?
의 각 단위 사각형에 점을 할당하여 이 타일의 각 쌍이 수평(또는 수직) 사각형에서 도미노를 사용할 수 있도록 할 수 있습니까? 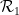 또는
또는 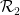 ?
?

실제로 각 Wang의 타일을 별도의 "점"으로 삽입하고 도미노 세트 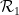 ,
, 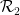 이 가로 또는 세로로 인접하도록 정의하기만 하면 되며 가장자리에는 Wang의 비밀 쌍이 있습니다. 같은 색.
이 가로 또는 세로로 인접하도록 정의하기만 하면 되며 가장자리에는 Wang의 비밀 쌍이 있습니다. 같은 색.
다음 단계에서는 도미노 문제와 스도쿠 문제를 결합해 보겠습니다.

문제 4(스도쿠 문제)
열 너비 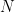 , 숫자 집합
, 숫자 집합 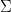 , 함수 집합
, 함수 집합 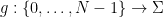
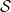 및 "초기 조건"
및 "초기 조건" 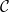 (여기서 자세히 설명하지 않음) "스도쿠 보드"
(여기서 자세히 설명하지 않음) "스도쿠 보드" 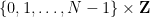 의 각 셀
의 각 셀 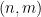 에 숫자
에 숫자 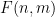 을 할당하여 모든 경사면
을 할당하여 모든 경사면 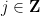 및 가로채기
및 가로채기 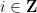 에 사용할 수 있습니까?
에 사용할 수 있습니까? 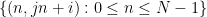 선에 있는 숫자
선에 있는 숫자 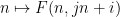 는
는 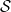 에 있습니다(그리고
에 있습니다(그리고 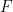 는 초기 조건
는 초기 조건 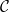 을 따릅니다)?
을 따릅니다)?
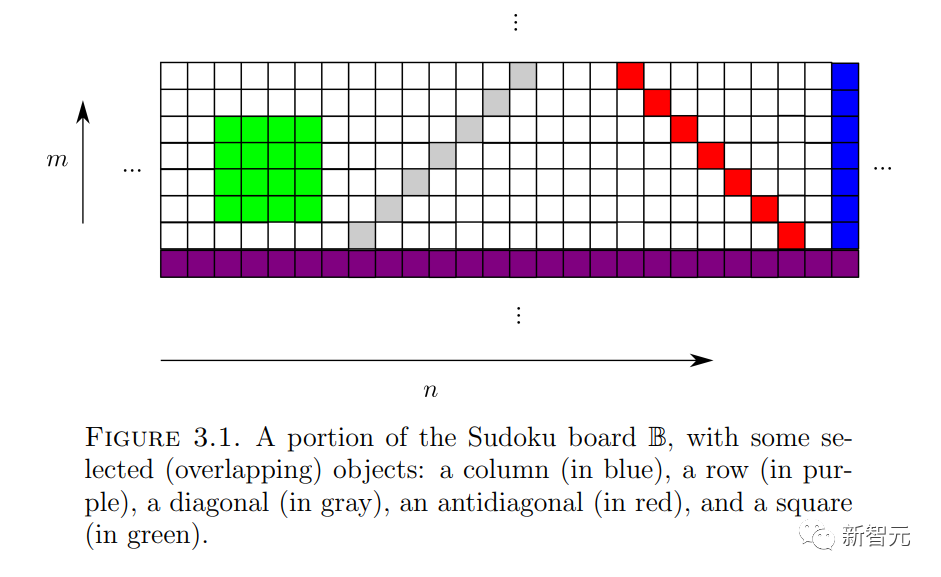
이 논문의 가장 참신한 부분은 도미노 문제가 실제로 스도쿠 문제에 포함될 수 있음을 증명하는 것입니다.
스도쿠 문제를 하나의 비밀 퍼즐에 포함시키는 것은 이전 논문에서 제안한 수정된 방법을 기반으로 합니다.
이 논문에서도 스도쿠 문제의 다른 버전을 제안하고 "암호 퍼즐"이라는 방법을 만들었습니다. 패딩 언어"는 다양한 문제(스도쿠 문제 포함)를 단일 포장 문제로 변환할 수 있습니다
도미노 문제를 스도쿠 문제로 인코딩하려면 도미노 함수를 얻어야 합니다
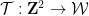 ( 일부 도미노 세트
( 일부 도미노 세트 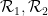 ) 이를 사용하여 스도쿠 기능
) 이를 사용하여 스도쿠 기능 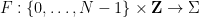 을 구축합니다(도미노 세트와 관련된 일부 스도쿠 제약 조건 준수). 반대로 각각은 숫자를 따릅니다. 스도쿠 퍼즐 규칙의 스도쿠 기능은 도미노에서 생성되어야 합니다. 어떤 방식으로든 기능합니다.
을 구축합니다(도미노 세트와 관련된 일부 스도쿠 제약 조건 준수). 반대로 각각은 숫자를 따릅니다. 스도쿠 퍼즐 규칙의 스도쿠 기능은 도미노에서 생성되어야 합니다. 어떤 방식으로든 기능합니다.
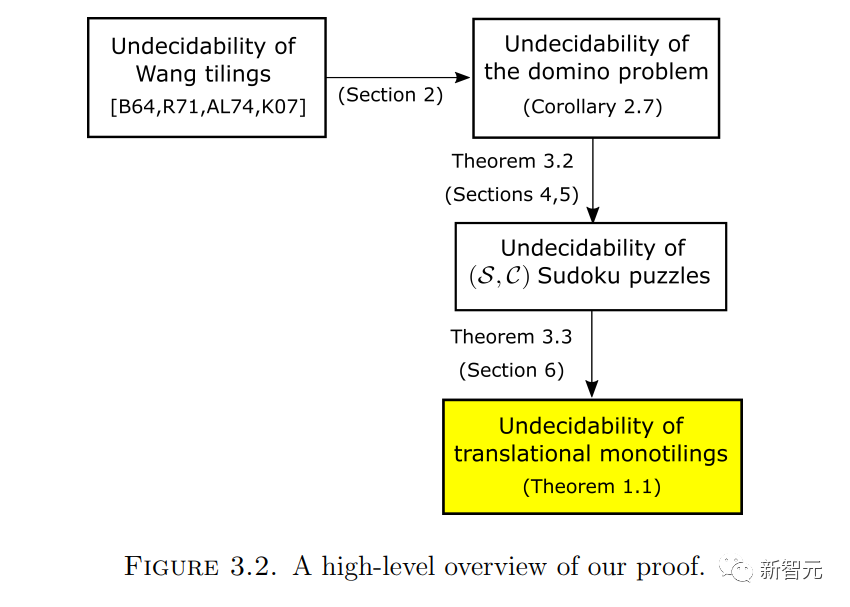
이 접근 방식은 즉시 명백하지는 않지만 Tao와 Rachel Greenfeld는 Emmanuel Jeandel의 도움을 받아 Aanderaa와 Lewis의 일부 아이디어를 적용했으며 특정 계층 구조를 사용하여 한 문제를 다른 문제로 인코딩했습니다.
여기서 계층 구조를 설명합니다 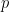 (도미노 문제의 2차원 특성으로 인해 두 개의 서로 다른 소수를 사용해야 함).
(도미노 문제의 2차원 특성으로 인해 두 개의 서로 다른 소수를 사용해야 함).
그런 다음 일종의 임베딩을 구현하는 공식 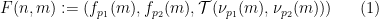 을 통해
을 통해 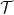 을 사용하여 스도쿠 함수
을 사용하여 스도쿠 함수 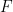 를 구축하세요.
를 구축하세요.
여기서 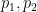 는 두 개의 서로 다른 큰 소수입니다(예:
는 두 개의 서로 다른 큰 소수입니다(예: 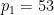 ,
, 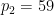 을 사용할 수 있음).
을 사용할 수 있음). 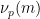 는
는 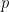 을
을 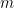 로 나눈 횟수를 나타냅니다.
로 나눈 횟수를 나타냅니다.
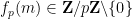 은
은 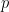 확장의 마지막 0이 아닌 숫자입니다.
확장의 마지막 0이 아닌 숫자입니다. 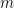
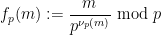 (
(
및 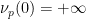 ).情况의 경우 (1)의 첫 번째 구성 요소는 다음과 같습니다.
).情况의 경우 (1)의 첫 번째 구성 요소는 다음과 같습니다. 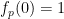
최종 가중치 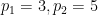 의 일반적인 예는 다음과 같습니다.
의 일반적인 예는 다음과 같습니다.
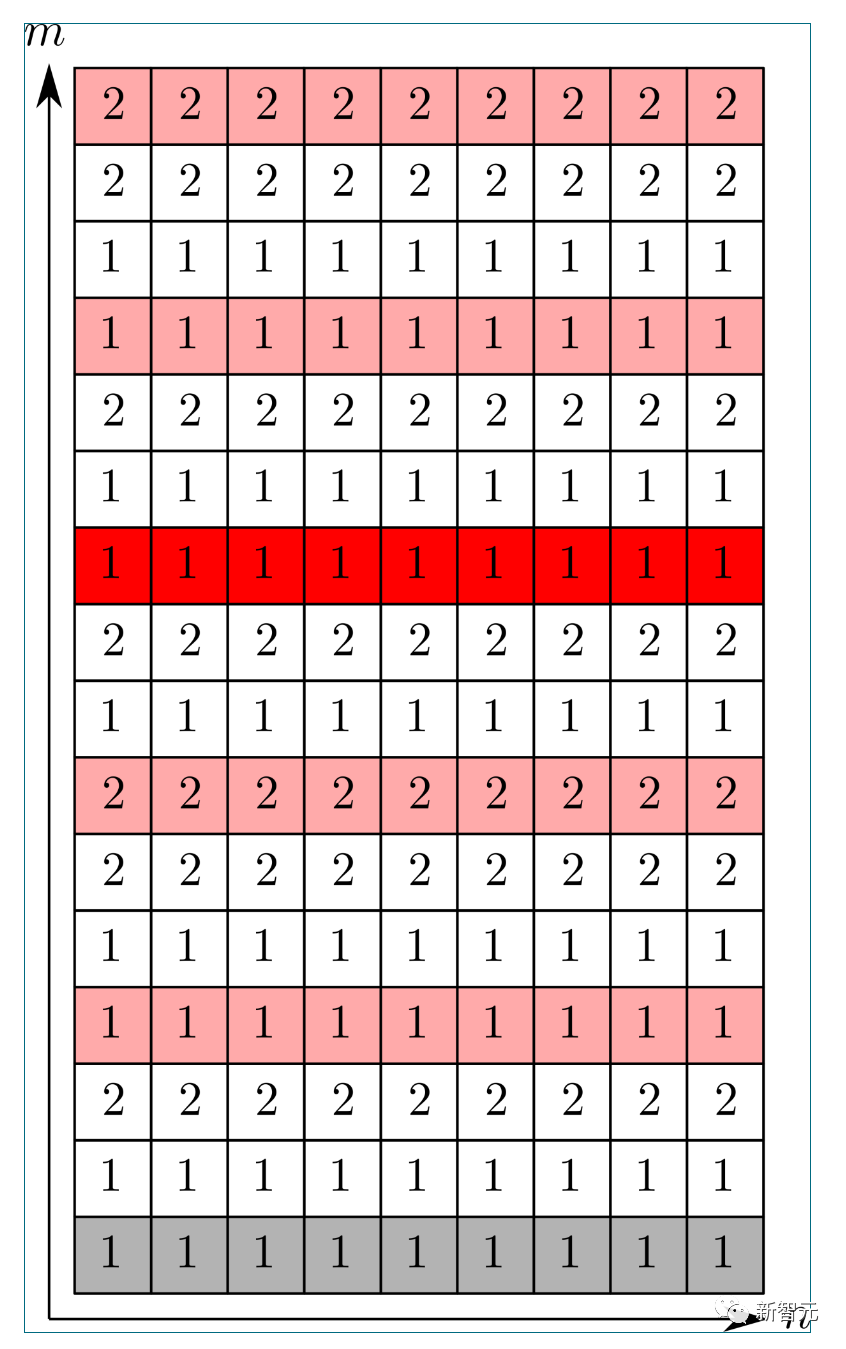
흥미롭게도 어떤 이유에서인지 , 여기 장식은 기본적으로 어린이 게임 "Fizz buzz"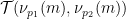 의 규칙을 따릅니다.
의 규칙을 따릅니다.
위 내용은 테렌스 타오(Terence Tao)가 또 다른 60년 기하학 문제에 접근합니다! 주기적인 밀착 포장 문제에 새로운 돌파구가 마련되었습니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7470
7470
 15
15
 1377
1377
 52
52
 77
77
 11
11
 48
48
 19
19
 19
19
 29
29
 AI가 수학적 연구를 전복시킨다! 필즈상 수상자이자 중국계 미국인 수학자, Terence Tao가 좋아하는 11개 논문 발표 |
Apr 09, 2024 am 11:52 AM
AI가 수학적 연구를 전복시킨다! 필즈상 수상자이자 중국계 미국인 수학자, Terence Tao가 좋아하는 11개 논문 발표 |
Apr 09, 2024 am 11:52 AM
AI는 실제로 수학을 변화시키고 있습니다. 최근 이 문제에 주목하고 있는 타오저쉬안(Tao Zhexuan)은 '미국수학회지(Bulletin of the American Mathematical Society)' 최신호를 게재했다. '기계가 수학을 바꿀 것인가?'라는 주제를 중심으로 많은 수학자들이 그들의 의견을 표현했습니다. 저자는 필즈상 수상자 Akshay Venkatesh, 중국 수학자 Zheng Lejun, 뉴욕대학교 컴퓨터 과학자 Ernest Davis 등 업계의 유명 학자들을 포함해 강력한 라인업을 보유하고 있습니다. AI의 세계는 극적으로 변했습니다. 이 기사 중 상당수는 1년 전에 제출되었습니다.
 칠각형 수
Sep 24, 2023 am 10:33 AM
칠각형 수
Sep 24, 2023 am 10:33 AM
칠각형 숫자는 칠각형으로 표현될 수 있는 숫자입니다. 칠각형 숫자는 칠각형으로 표현될 수 있습니다. 칠각형 숫자는 칠각형(7면 다각형)의 연속적인 레이어의 조합으로 표현될 수 있습니다. 칠각형 숫자는 아래 그림으로 더 잘 설명될 수 있습니다. 그러므로,
 획기적인 CVM 알고리즘으로 40년 이상의 계산 문제를 해결합니다! 컴퓨터 과학자가 동전을 던져 '햄릿'이라는 고유한 단어를 알아냈습니다.
Jun 07, 2024 pm 03:44 PM
획기적인 CVM 알고리즘으로 40년 이상의 계산 문제를 해결합니다! 컴퓨터 과학자가 동전을 던져 '햄릿'이라는 고유한 단어를 알아냈습니다.
Jun 07, 2024 pm 03:44 PM
계산하는 것은 간단해 보이지만 실제로는 매우 어렵습니다. 야생동물 인구조사를 실시하기 위해 깨끗한 열대우림으로 이동했다고 상상해 보세요. 동물을 볼 때마다 사진을 찍어보세요. 디지털 카메라는 추적된 동물의 총 수만 기록하는데, 고유한 동물의 수에 관심이 있지만 통계가 없습니다. 그렇다면 이 독특한 동물 집단에 접근하는 가장 좋은 방법은 무엇입니까? 이 시점에서 지금부터 세기 시작하고 마지막으로 사진의 새로운 종을 목록과 비교해야 합니다. 그러나 이 일반적인 계산 방법은 최대 수십억 개의 항목에 달하는 정보에 적합하지 않은 경우가 있습니다. 인도 통계 연구소, UNL 및 싱가포르 국립 대학교의 컴퓨터 과학자들이 새로운 알고리즘인 CVM을 제안했습니다. 긴 목록에 있는 다양한 항목의 계산을 대략적으로 계산할 수 있습니다.
 MLP가 하룻밤 사이에 사망했습니다! MIT Caltech 및 기타 혁신적인 KAN, 기록을 깨고 DeepMind를 무너뜨린 수학적 정리 발견
May 06, 2024 pm 03:10 PM
MLP가 하룻밤 사이에 사망했습니다! MIT Caltech 및 기타 혁신적인 KAN, 기록을 깨고 DeepMind를 무너뜨린 수학적 정리 발견
May 06, 2024 pm 03:10 PM
하룻밤 사이에 머신러닝 패러다임이 곧 바뀔 것입니다! 오늘날 딥 러닝 분야를 지배하는 인프라는 뉴런에 활성화 기능을 배치하는 다층 퍼셉트론(MLP)입니다. 그렇다면 그 외에 우리가 취할 수 있는 새로운 경로는 없을까요? 바로 오늘 MIT, Caltech, Northeastern University 및 기타 기관의 팀이 새로운 신경망 구조인 Kolmogorov-Arnold Networks(KAN)를 출시했습니다. 연구원들은 학습 가능한 활성화 함수를 노드(뉴런)에서 에지(가중치)로 이동하여 MLP를 간단하게 변경했습니다! 논문 주소: https://arxiv.org/pdf/2404.19756 이 변경 사항은 언뜻 보면 근거가 없어 보입니다.
 AI 그림에는 여전히 수학을 알아야 합니까?
Jun 12, 2023 pm 02:05 PM
AI 그림에는 여전히 수학을 알아야 합니까?
Jun 12, 2023 pm 02:05 PM
비전 인공지능 기술의 발전으로 요즘 AI 페인팅이 화제가 되고 있습니다. 인공지능은 딥러닝 알고리즘을 사용하여 사실적인 이미지를 생성하여 놀라운 예술 작품을 만들 수 있습니다. 이러한 놀라운 작품의 이면에는 수학적 지식의 뒷받침이 있습니다. 수학적 모델은 AI 페인팅에서 중요한 역할을 합니다. 한편, 수학적 모델은 이미지 정보를 설명하고 표현하는 데 사용되며, 이를 통해 컴퓨터는 이미지를 이해하고 처리할 수 있습니다. 반면, 수학적 모델은 이미지 자동 생성을 달성하기 위해 딥 러닝 모델을 훈련하는 데에도 사용됩니다. 딥러닝 모델은 고품질 이미지 생성을 제공합니다. 딥러닝 모델은 AI 페인팅의 핵심 부분입니다. 대량의 영상 데이터를 학습하고 다단계 데이터 처리를 통해 영상의 특성을 파악하고 시뮬레이션합니다.
 확산 모델 뒤에 숨은 수학은 소화하기 너무 어렵나요? Google은 통일된 관점으로 이를 명확하게 설명합니다.
Apr 11, 2023 pm 07:46 PM
확산 모델 뒤에 숨은 수학은 소화하기 너무 어렵나요? Google은 통일된 관점으로 이를 명확하게 설명합니다.
Apr 11, 2023 pm 07:46 PM
최근 AI 페인팅이 큰 인기를 끌고 있다. AI의 페인팅 기능에 감탄하면서도 확산 모델이 큰 역할을 한다는 사실은 알지 못할 수도 있습니다. 인기 모델인 OpenAI의 DALL·E 2를 예로 들어 보겠습니다. 간단한 텍스트(프롬프트)만 입력하면 1024*1024 고화질 이미지를 여러 개 생성할 수 있습니다. DALL·E 2가 발표된 지 얼마 지나지 않아 Google은 주어진 텍스트 설명에서 장면의 사실적인 이미지를 생성할 수 있는 텍스트-이미지 AI 모델인 Imagen을 출시했습니다. 불과 며칠 전 Stability.Ai는 텍스트 생성 이미지 모델 Stable Diffusi를 공개했습니다.
 '수학적 멍청한 놈' ChatGPT는 인간의 선호도를 매우 잘 이해합니다! 온라인에서 난수를 생성하는 것은 우주에 대한 궁극적인 해답입니다
Apr 01, 2023 am 11:48 AM
'수학적 멍청한 놈' ChatGPT는 인간의 선호도를 매우 잘 이해합니다! 온라인에서 난수를 생성하는 것은 우주에 대한 궁극적인 해답입니다
Apr 01, 2023 am 11:48 AM
ChatGPT는 또한 난수 생성과 관련하여 인간의 속임수를 이해합니다. ChatGPT는 헛소리 예술가이자 잘못된 정보를 퍼뜨리는 사람일 수 있지만 "수학자"는 아닙니다! 최근 메타 데이터 과학자인 Colin Fraser는 ChatGPT가 진정한 난수를 생성할 수 없고 "인간 난수"에 더 가깝다는 사실을 발견했습니다. 실험을 통해 프레이저는 "ChatGPT는 숫자 42와 7을 매우 좋아한다"고 결론지었습니다. 네티즌들은 이는 인간이 이 숫자를 매우 좋아한다는 것을 의미한다고 말했습니다. ChatGPT는 또한 "The Ultimate Answer to the Universe"를 좋아합니다. 테스트에서 Fraser가 입력한 프롬프트는 다음과 같습니다. "임의의 숫자를 선택하세요.
 낮에는 일하고 밤에는 연구를 수행하는 Google Brain 연구 과학자들은 수십 년 동안 수학계를 곤혹스럽게 만들었던 추측을 풀었습니다.
Apr 12, 2023 am 09:49 AM
낮에는 일하고 밤에는 연구를 수행하는 Google Brain 연구 과학자들은 수십 년 동안 수학계를 곤혹스럽게 만들었던 추측을 풀었습니다.
Apr 12, 2023 am 09:49 AM
2022년 10월 중순, 저스틴 길머는 동부 해안에 있는 러트거스 대학교의 수학자이자 전 멘토였던 마이클 삭스를 만나기 위해 캘리포니아에서 뉴욕으로 날아갔습니다. 회상하는 동안 그들은 수학에 관해 이야기하지 않았습니다. 실제로 길머는 2015년 러트거스 대학교에서 박사 학위를 취득한 이후로 수학에 대해 진지하게 생각해 본 적이 없습니다. 그 당시 그는 학계에서 경력을 쌓지 않기로 결정하고 프로그래밍을 독학하기 시작했습니다. Saks와 저녁 식사를 하면서 Gilmer는 멘토에게 Google에서 하는 일, 즉 기계 학습과 인공 지능에 대해 이야기했습니다. 캠퍼스 길을 따라 걸으며 길머는 2013년에 이 길을 걷는 데 1년이 넘는 시간을 보냈다고 회상했다.




