PyTorch를 사용하여 노이즈 제거 확산 모델 구현
DDPM(Denoising Diffusion Probabilistic Model)의 작동 원리를 자세히 이해하기 전에, 먼저 DDPM의 기초 연구 중 하나인 생성 인공지능(Generative Artificial Intelligence)의 발전 과정을 먼저 이해해 보겠습니다.

VAE
VAE는 인코더, 확률적 잠재 공간 및 디코더를 사용합니다. 훈련 중에 인코더는 각 이미지의 평균과 분산을 예측하고 가우스 분포에서 이러한 값을 샘플링합니다. 샘플링 결과는 디코더로 전달되어 입력 이미지를 출력 이미지와 유사한 형태로 변환합니다. KL 발산은 손실을 계산하는 데 사용됩니다. VAE의 중요한 장점은 다양한 이미지를 생성할 수 있다는 것입니다. 샘플링 단계에서는 가우스 분포에서 직접 샘플링하고 디코더를 통해 새로운 이미지를 생성할 수 있습니다.
GAN
변형 자동 인코더(VAE)가 나온 지 불과 1년 만에 획기적인 생성 모델 제품군이 등장했습니다. 생성적 적대 네트워크(GAN)는 생성 모델의 새로운 클래스를 제시합니다. 두 개의 신경망(생성자와 판별자)의 협력에는 적대적 훈련 프로세스가 포함됩니다. 생성기의 목적은 무작위 노이즈로부터 이미지와 같은 실제 데이터를 생성하는 것이고, 판별기는 생성된 데이터와 실제 데이터를 구별하려고 노력합니다. 훈련 단계 전반에 걸쳐 생성자와 판별자는 경쟁력 있는 학습 프로세스를 통해 지속적으로 능력을 향상시킵니다. 생성기는 점점 더 확실한 데이터를 생성하므로 판별기보다 더 똑똑해지며 결과적으로 실제 샘플과 생성된 샘플을 구별하는 능력이 향상됩니다. 이러한 적대적 상호작용은 고품질의 현실적인 데이터를 생성하는 생성기에서 정점에 이릅니다. 샘플링 단계에서는 GAN 훈련 후 생성기가 무작위 노이즈를 입력하여 새로운 샘플을 생성합니다. 이 노이즈를 일반적으로 실제 사례를 반영하는 데이터로 변환합니다.
다른 모델 아키텍처가 필요한 이유
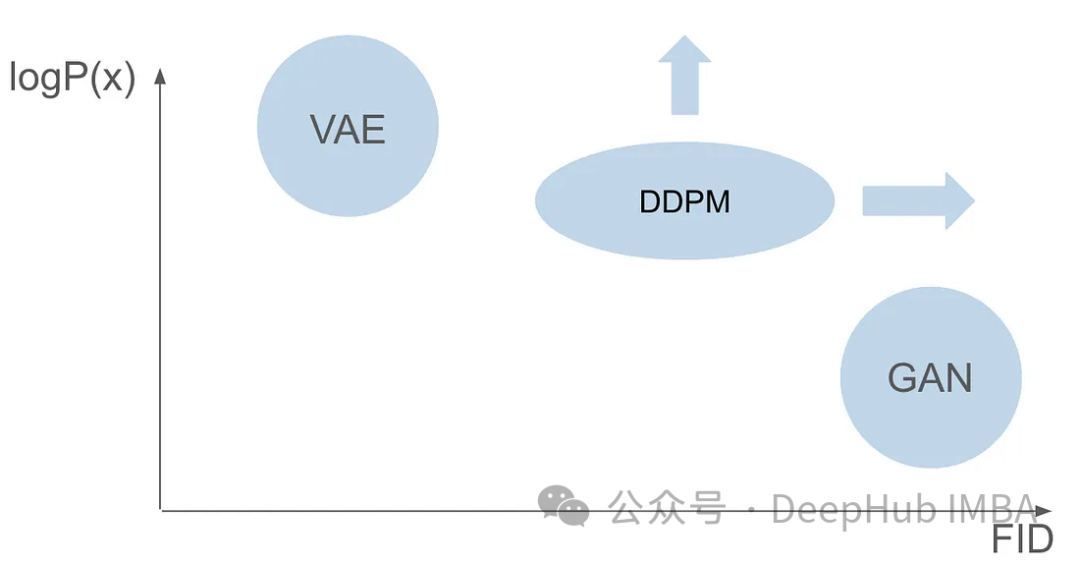
GAN과 VAE는 이미지 생성에 있어 장점이 있지만 둘 다 몇 가지 문제가 있습니다. GAN은 훈련 세트의 이미지와 매우 유사한 사실적인 이미지를 생성할 수 있지만 생성된 결과에는 다양성이 부족합니다. VAE는 다양한 이미지를 생성할 수 있지만 흐릿한 이미지를 생성하는 경향이 있습니다. 그러나 이 두 가지 기능을 결합하여 매우 사실적이고 다양한 이미지를 만드는 데는 성공하지 못했습니다. 이 과제는 연구자들에게 중요한 장애물이며 해결되어야 합니다. 따라서 향후 연구 방향 중 하나는 GAN과 VAE의 장점을 결합하여 매우 현실적이고 다양한 이미지 생성을 달성하는 방법을 모색하는 것입니다. 이는 이미지 생성 분야에 획기적인 발전을 가져올 것이며 다양한 분야에서 널리 사용될 것입니다.
GAN 논문이 출판된 지 6년, VAE 논문이 출판된 지 7년 후, 획기적인 모델, 즉 DDPM(Denoising Diffusion Probabilistic Model)이 등장했습니다. DDPM은 두 분야의 장점을 결합하여 다양하고 사실적인 이미지를 만들어냅니다.
이 기사에서는 교육 프로세스, 정방향 및 역방향 프로세스, 샘플링 방법을 포함하여 DDPM의 복잡성을 자세히 살펴봅니다. 우리는 PyTorch를 사용하여 처음부터 DDPM을 구축하고 교육하여 독자들에게 전체 프로세스를 안내할 것입니다.
여러분은 이미 딥러닝의 기초에 익숙하고 딥 컴퓨터 비전에 대한 탄탄한 기초를 갖추고 있다고 가정합니다. 우리는 이러한 기본 개념에 대해 자세히 설명하지 않고 대신 진정성을 믿을 수 있는 이미지를 생성하는 데 중점을 둘 것입니다.
DDPM
DDPM(Denoising Diffusion Probabilistic Model)은 생성 모델 분야의 최첨단 방법입니다. 명시적 우도 함수에 의존하는 기존 모델과 비교하여 DDPM은 반복적인 노이즈 제거 확산 프로세스를 통해 작동합니다. 이 프로세스에는 이미지에 점차적으로 노이즈를 추가하고 해당 노이즈를 제거하는 작업이 포함됩니다. 기본 이론은 일련의 확산 단계를 통해 단순한 분포(예: 가우시안 분포)를 복잡하고 표현력이 풍부한 이미지 데이터 분포로 변환한다는 아이디어를 기반으로 합니다. 즉, 원본 이미지 분포에서 가우스 분포로 샘플을 이동함으로써 이 프로세스를 역전시키는 모델을 구축할 수 있습니다. 이를 통해 완전 가우스 분포에서 시작하여 이미지 분포 특성을 가진 새로운 이미지를 생성하여 효율적인 이미지 생성을 달성할 수 있습니다.
DDPM 교육은 두 가지 기본 단계, 즉 고정되고 학습할 수 없는 시끄러운 이미지를 생성하는 순방향 프로세스와 후속 역방향 프로세스로 구성됩니다. 역 프로세스의 주요 목표는 특수 기계 학습 모델을 사용하여 이미지의 노이즈를 제거하는 것입니다.
순방향 확산 프로세스
순방향 프로세스는 고정되고 학습할 수 없는 단계이지만 미리 정의된 몇 가지 설정이 필요합니다. 설정에 들어가기 전에 먼저 작동 방식을 이해해 보겠습니다.
이 프로세스의 핵심 개념은 선명한 이미지에서 시작하는 것입니다. "T"로 표시된 특정 단계 크기에서는 가우스 분포를 따라 소량의 노이즈가 점차 도입됩니다.

이미지에서 볼 수 있듯이 각 단계에서 노이즈가 증가하고 있습니다. 이 노이즈의 수학적 표현을 살펴보겠습니다.
노이즈는 가우스 분포에서 샘플링됩니다. 각 단계에서 소량의 노이즈를 도입하기 위해 Markov 체인을 사용합니다. 현재 타임스탬프의 이미지를 생성하려면 마지막 타임스탬프의 이미지만 필요합니다. 마르코프 체인의 개념은 여기서 핵심이며 이후의 수학적 세부 사항에 매우 중요합니다.
마르코프 체인은 특정 상태로의 전환 확률이 이전 이벤트 시퀀스가 아닌 현재 상태와 경과 시간에만 의존하는 확률론적 프로세스입니다. 이 기능은 노이즈 추가 프로세스의 모델링을 단순화하여 수학적으로 분석하기를 더 쉽게 만듭니다.
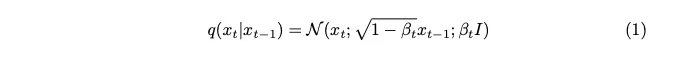
베타로 표현되는 분산 매개변수는 각 단계에서 최소한의 노이즈만 도입하기 위해 의도적으로 매우 작은 값으로 설정됩니다.
단계 매개변수 "T"는 완전히 노이즈가 있는 이미지를 생성하는 데 필요한 단계 크기를 결정합니다. 이 글에서는 이 매개변수를 1000으로 설정했는데, 꽤 커 보일 수 있습니다. 데이터 세트의 모든 원본 이미지에 대해 1000개의 노이즈 이미지를 생성해야 합니까? Markov 체인 측면이 이 문제를 해결하는 데 도움이 되는 것으로 입증되었습니다. 다음 단계를 예측하려면 이전 단계의 이미지만 필요하고 각 단계에서 추가된 노이즈는 동일하게 유지되므로 특정 타임스탬프에서 노이즈 이미지를 생성하여 계산을 단순화할 수 있습니다. 쌍 재매개변수화 기술을 사용하면 방정식을 더욱 단순화할 수 있습니다.
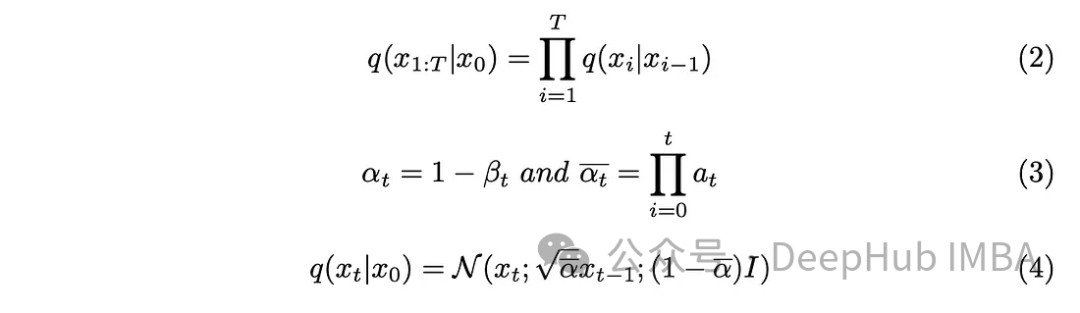
식(3)에 도입된 새로운 매개변수를 식(2)에 통합하고 식(2)를 전개하여 결과를 얻습니다.
역 확산 과정
이미지에 노이즈를 도입했으며 다음 단계는 역확산 과정을 수행하는 것입니다. 초기 조건, 즉 t = 0에서 노이즈가 제거되지 않은 이미지를 알지 못하는 한, 이미지의 노이즈를 제거하기 위해 역과정을 수학적으로 구현하는 것은 불가능합니다. 우리의 목표는 노이즈에서 직접 샘플링하여 새로운 이미지를 만드는 것인데, 여기에는 결과에 대한 정보가 부족합니다. 따라서 결과를 알지 못한 채 이미지의 노이즈를 점진적으로 제거하는 방법을 고안해야 합니다. 그래서 이 복잡한 수학적 함수를 근사화하기 위해 딥 러닝 모델을 사용하는 솔루션이 등장했습니다.
약간의 수학적 배경을 사용하여 모델은 방정식 (5)를 근사화합니다. 주목할 만한 한 가지 세부 사항은 원본 DDPM 논문을 고수하고 분산을 고정된 상태로 유지하면서 모델이 이를 학습하도록 하는 것도 가능하다는 것입니다.
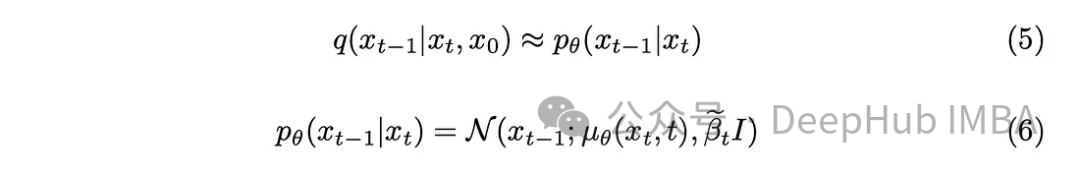
모델의 임무는 현재 타임스탬프와 이전 타임스탬프 사이에 추가된 노이즈의 평균을 예측하는 것입니다. 이렇게 하면 노이즈를 효과적으로 제거하고 원하는 효과를 얻을 수 있습니다. 하지만 우리의 목표가 "원본 이미지"에서 마지막 타임스탬프에 추가된 노이즈를 모델이 예측하도록 하는 것이라면 어떨까요?
노이즈가 없는 초기 이미지를 알지 못하면 역과정을 수행하는 것이 수학적으로 어렵습니다. 사후 분산을 정의함으로써.

모델의 임무는 초기 이미지로부터 타임스탬프 t에서 이미지에 추가되는 노이즈를 예측하는 것입니다. 순방향 프로세스를 사용하면 선명한 이미지에서 시작하여 타임스탬프 t에서 노이즈가 있는 이미지로 진행하는 이 작업을 수행할 수 있습니다.
훈련 알고리즘
예측에 사용되는 모델 아키텍처가 U-Net이라고 가정합니다. 훈련 단계의 목표는 데이터 세트의 각 이미지에 대해 [0, T] 범위의 타임스탬프를 무작위로 선택하고 순방향 확산 프로세스를 계산하는 것입니다. 이는 사용된 실제 노이즈뿐만 아니라 명확하고 다소 노이즈가 있는 이미지를 생성합니다. 그런 다음 이 모델은 역과정에 대한 이해를 바탕으로 이미지에 추가되는 노이즈를 예측하는 데 사용됩니다. 실제 노이즈와 예측 노이즈를 통해 우리는 지도형 기계 학습 문제에 들어간 것으로 보입니다.
모델을 훈련하기 위해 어떤 손실 함수를 사용해야 할까요? 우리가 확률적 잠재 공간을 다루기 때문에 Kullback-Leibler(KL) 발산이 적합한 선택입니다.
KL 발산은 두 확률 분포(이 경우에는 모델에서 예측한 분포와 예상 분포) 간의 차이를 측정합니다. KL 발산을 손실 함수에 통합하면 모델이 정확한 예측을 생성하도록 안내할 뿐만 아니라 잠재 공간 표현이 원하는 확률 구조를 준수하도록 보장합니다.
KL 발산은 L2 손실 함수로 근사화할 수 있으므로 다음과 같은 손실 함수를 얻을 수 있습니다.
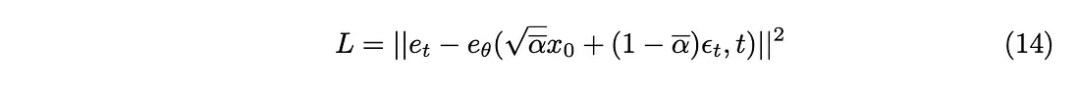
마지막으로 논문에서 제안한 훈련 알고리즘을 얻습니다.

Sampling
역과정을 설명했으니, 사용법은 이렇습니다. 시간 T의 완전히 무작위적인 이미지에서 시작하여 역과정을 T번 수행하면 마침내 시간 0에 도달합니다. 이는 이 기사에 설명된 두 번째 알고리즘을 형성합니다.

매개변수
베타, beta_tildes, 알파, alpha_hat 등 다양한 매개변수가 있습니다. 이 매개변수를 선택하는 방법을 아직 모르겠습니다. 그러나 이 시점에서 알려진 유일한 매개변수는 1000으로 설정된 T입니다.
나열된 모든 매개변수의 경우 베타에 따라 선택이 달라집니다. 어떤 의미에서 Beta는 각 단계에서 추가하려는 노이즈의 양을 결정합니다. 따라서 알고리즘의 성공을 보장하려면 신중한 베타 선택이 중요합니다. 그 외 변수가 너무 많기 때문에 논문을 참고하시기 바랍니다.
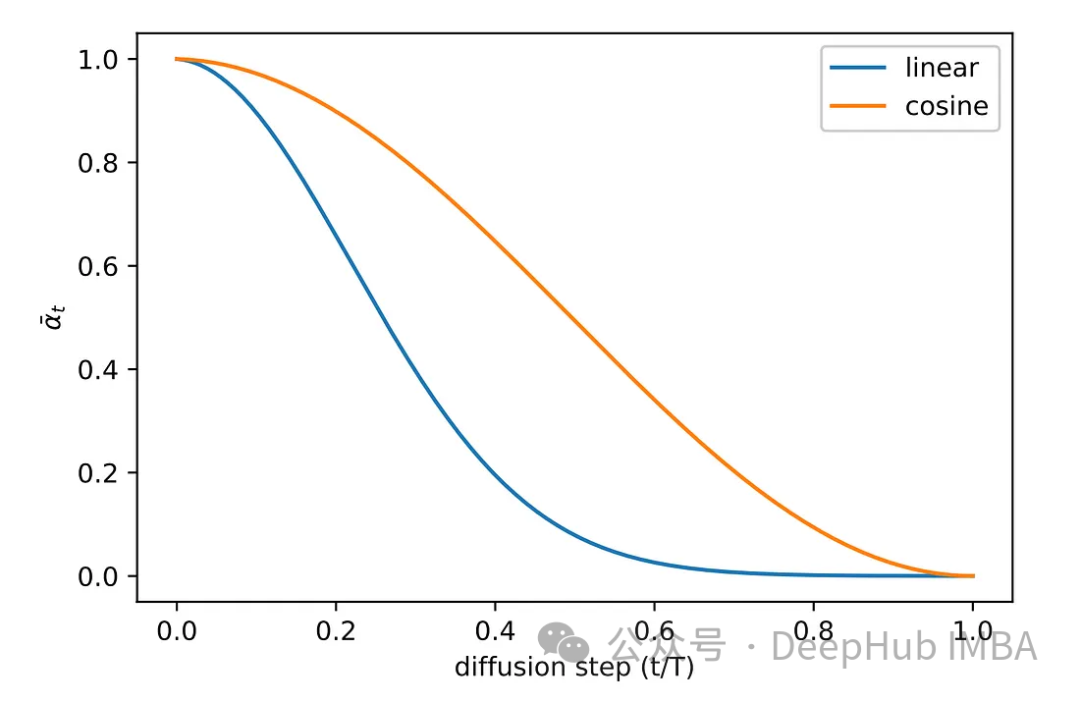
원고의 실험 단계에서 다양한 샘플링 방법을 모색했습니다. 원래의 선형 샘플링 방법 이미지는 노이즈가 충분하지 않거나 너무 노이즈가 발생했습니다. 이 문제를 해결하기 위해 또 다른 일반적인 방법, 즉 코사인 샘플링이 채택됩니다. 코사인 샘플링은 더욱 부드럽고 일관된 노이즈 추가를 제공합니다.
모델 Pytorch 구현
U-Net 아키텍처를 노이즈 예측에 활용하겠습니다. U-Net을 선택한 이유는 U-Net이 이미지 처리, 공간 캡처 및 기능에 가장 적합하기 때문입니다. 동일한 출력 크기에 이상적인 아키텍처를 제공하고 입력합니다.
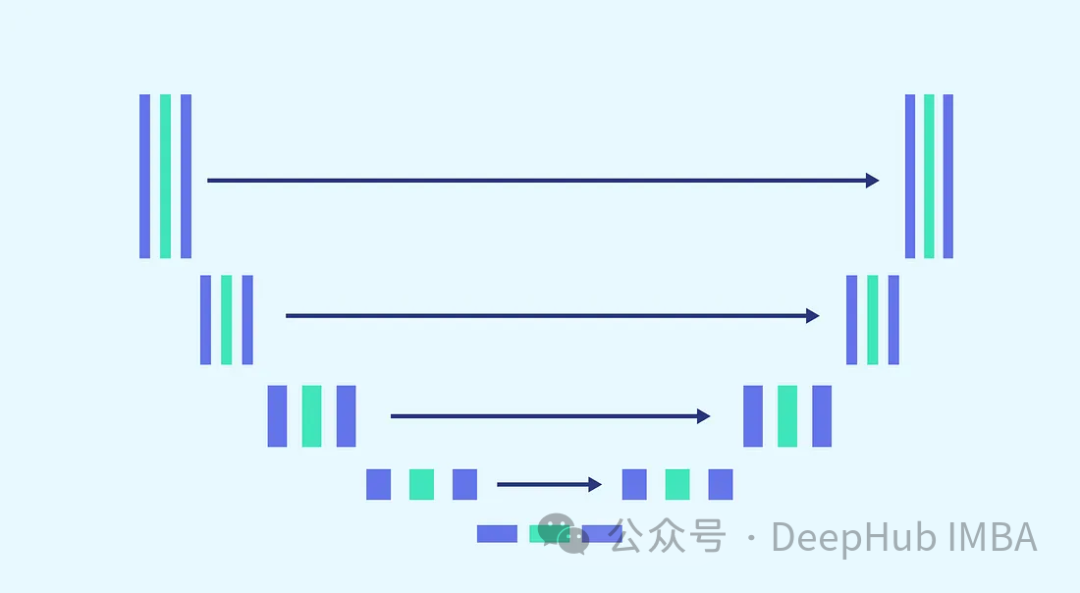
작업의 복잡성과 모든 단계에서 동일한 모델을 사용해야 한다는 요구 사항을 고려하여(모델은 동일한 가중치로 완전히 노이즈가 많은 이미지와 약간 노이즈가 많은 이미지를 제거할 수 있어야 함) 모델을 조정합니다. 필수 불가결합니다. 여기에는 보다 복잡한 블록을 병합하고 정현파 임베딩 단계를 통해 사용되는 타임스탬프에 대한 인식을 도입하는 것이 포함됩니다. 이러한 개선의 목적은 모델을 잡음 제거 작업의 전문가로 만드는 것입니다. 전체 모델 구축을 진행하기 전에 각 블록을 소개하겠습니다.
ConvNext Block
모델 복잡성을 높여야 하는 요구 사항을 충족하기 위해 컨볼루션 블록은 중요한 역할을 합니다. 여기서는 u-net 논문의 기본 블록에만 의존할 수 없으며 이를 ConvNext와 결합할 것입니다.
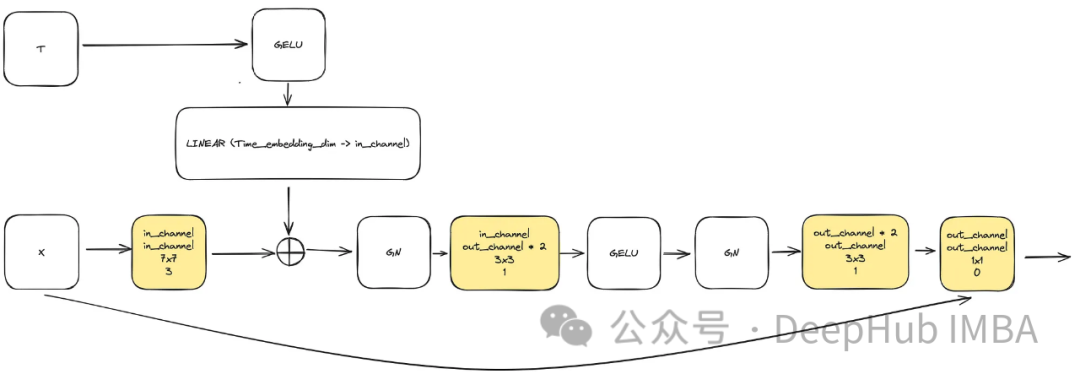
입력은 이미지를 나타내는 "x"와 "time_embedding_dim" 크기의 내장된 타임스탬프 시각화 "t"로 구성됩니다. 프로세스 전반에 걸쳐 블록은 복잡성과 입력 및 최종 레이어에 대한 잔여 연결로 인해 공간 및 기능 맵을 학습하는 데 중요한 역할을 합니다.
class ConvNextBlock(nn.Module):def __init__(self,in_channels,out_channels,mult=2,time_embedding_dim=None,norm=True,group=8,):super().__init__()self.mlp = (nn.Sequential(nn.GELU(), nn.Linear(time_embedding_dim, in_channels))if time_embedding_dimelse None) self.in_conv = nn.Conv2d(in_channels, in_channels, 7, padding=3, groups=in_channels) self.block = nn.Sequential(nn.GroupNorm(1, in_channels) if norm else nn.Identity(),nn.Conv2d(in_channels, out_channels * mult, 3, padding=1),nn.GELU(),nn.GroupNorm(1, out_channels * mult),nn.Conv2d(out_channels * mult, out_channels, 3, padding=1),) self.residual_conv = (nn.Conv2d(in_channels, out_channels, 1)if in_channels != out_channelselse nn.Identity()) def forward(self, x, time_embedding=None):h = self.in_conv(x)if self.mlp is not None and time_embedding is not None:assert self.mlp is not None, "MLP is None"h = h + rearrange(self.mlp(time_embedding), "b c -> b c 1 1")h = self.block(h)return h + self.residual_conv(x)
정현파 타임스탬프 임베딩
모델의 핵심 블록 중 하나는 정현파 타임스탬프 임베딩 블록입니다. 이를 통해 주어진 타임스탬프를 인코딩하여 모델이 디코딩하는 데 필요한 현재 시간에 대한 정보를 유지할 수 있습니다. 모델은 모든 다른 타임스탬프에 사용됩니다. this 이것은 매우 고전적인 구현이며 다양한 장소에 적용되며 코드를 직접 붙여 넣습니다. 이 모듈은 이를 활용하여 주어진 타임스탬프 t를 기반으로 시간 표현을 생성합니다. 이 MLP(다층 퍼셉트론)의 출력은 수정된 모든 ConvNext 블록에 대한 입력 "t" 역할도 합니다.
여기서 "dim"은 모델의 하이퍼파라미터로 첫 번째 블록에 필요한 채널 수를 나타냅니다. 이는 후속 블록의 채널 수에 대한 기본 계산 역할을 합니다. class SinusoidalPosEmb(nn.Module):def __init__(self, dim, theta=10000):super().__init__()self.dim = dimself.theta = theta def forward(self, x):device = x.devicehalf_dim = self.dim // 2emb = math.log(self.theta) / (half_dim - 1)emb = torch.exp(torch.arange(half_dim, device=device) * -emb)emb = x[:, None] * emb[None, :]emb = torch.cat((emb.sin(), emb.cos()), dim=-1)return emb
로그인 후 복사
class SinusoidalPosEmb(nn.Module):def __init__(self, dim, theta=10000):super().__init__()self.dim = dimself.theta = theta def forward(self, x):device = x.devicehalf_dim = self.dim // 2emb = math.log(self.theta) / (half_dim - 1)emb = torch.exp(torch.arange(half_dim, device=device) * -emb)emb = x[:, None] * emb[None, :]emb = torch.cat((emb.sin(), emb.cos()), dim=-1)return emb
Attention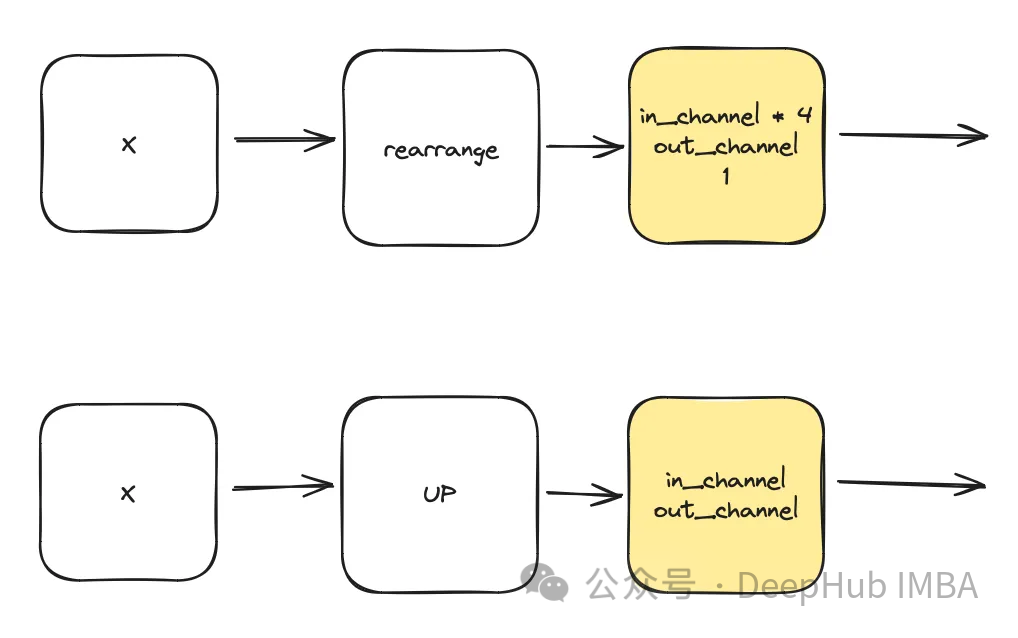
이것은 unet에서 사용되는 선택적 구성 요소입니다. 주의는 학습에서 잔여 연결의 역할을 향상시키는 데 도움이 됩니다. 잔여 연결로 계산된 Attention 메커니즘과 중간 및 낮은 잠재 공간으로 계산된 특징 맵을 통해 Unet의 왼쪽에서 얻은 중요한 공간 정보에 더 많은 관심을 기울입니다. ACC-UNet 논문에서 나온 것입니다.
gate는 하위 블록의 업샘플링된 출력을 나타내고, x-residual은 주의가 적용되는 수준의 잔여 연결을 나타냅니다. 
class BlockAttention(nn.Module):def __init__(self, gate_in_channel, residual_in_channel, scale_factor):super().__init__()self.gate_conv = nn.Conv2d(gate_in_channel, gate_in_channel, kernel_size=1, stride=1)self.residual_conv = nn.Conv2d(residual_in_channel, gate_in_channel, kernel_size=1, stride=1)self.in_conv = nn.Conv2d(gate_in_channel, 1, kernel_size=1, stride=1)self.relu = nn.ReLU()self.sigmoid = nn.Sigmoid() def forward(self, x: torch.Tensor, g: torch.Tensor) -> torch.Tensor:in_attention = self.relu(self.gate_conv(g) + self.residual_conv(x))in_attention = self.in_conv(in_attention)in_attention = self.sigmoid(in_attention)return in_attention * x
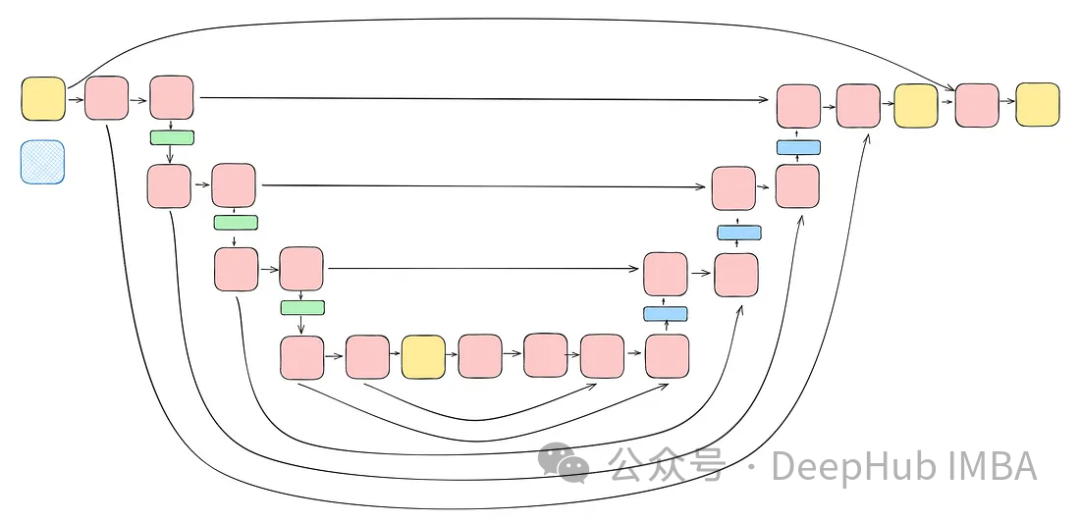
最后整合
将前面讨论的所有块(不包括注意力块)整合到一个Unet中。每个块都包含两个残差连接,而不是一个。这个修改是为了解决潜在的过度拟合问题。
class TwoResUNet(nn.Module):def __init__(self,dim,init_dim=None,out_dim=None,dim_mults=(1, 2, 4, 8),channels=3,sinusoidal_pos_emb_theta=10000,convnext_block_groups=8,):super().__init__()self.channels = channelsinput_channels = channelsself.init_dim = default(init_dim, dim)self.init_conv = nn.Conv2d(input_channels, self.init_dim, 7, padding=3) dims = [self.init_dim, *map(lambda m: dim * m, dim_mults)]in_out = list(zip(dims[:-1], dims[1:])) sinu_pos_emb = SinusoidalPosEmb(dim, theta=sinusoidal_pos_emb_theta) time_dim = dim * 4 self.time_mlp = nn.Sequential(sinu_pos_emb,nn.Linear(dim, time_dim),nn.GELU(),nn.Linear(time_dim, time_dim),) self.downs = nn.ModuleList([])self.ups = nn.ModuleList([])num_resolutions = len(in_out) for ind, (dim_in, dim_out) in enumerate(in_out):is_last = ind >= (num_resolutions - 1) self.downs.append(nn.ModuleList([ConvNextBlock(in_channels=dim_in,out_channels=dim_in,time_embedding_dim=time_dim,group=convnext_block_groups,),ConvNextBlock(in_channels=dim_in,out_channels=dim_in,time_embedding_dim=time_dim,group=convnext_block_groups,),DownSample(dim_in, dim_out)if not is_lastelse nn.Conv2d(dim_in, dim_out, 3, padding=1),])) mid_dim = dims[-1]self.mid_block1 = ConvNextBlock(mid_dim, mid_dim, time_embedding_dim=time_dim)self.mid_block2 = ConvNextBlock(mid_dim, mid_dim, time_embedding_dim=time_dim) for ind, (dim_in, dim_out) in enumerate(reversed(in_out)):is_last = ind == (len(in_out) - 1)is_first = ind == 0 self.ups.append(nn.ModuleList([ConvNextBlock(in_channels=dim_out + dim_in,out_channels=dim_out,time_embedding_dim=time_dim,group=convnext_block_groups,),ConvNextBlock(in_channels=dim_out + dim_in,out_channels=dim_out,time_embedding_dim=time_dim,group=convnext_block_groups,),Upsample(dim_out, dim_in)if not is_lastelse nn.Conv2d(dim_out, dim_in, 3, padding=1)])) default_out_dim = channelsself.out_dim = default(out_dim, default_out_dim) self.final_res_block = ConvNextBlock(dim * 2, dim, time_embedding_dim=time_dim)self.final_conv = nn.Conv2d(dim, self.out_dim, 1) def forward(self, x, time):b, _, h, w = x.shapex = self.init_conv(x)r = x.clone() t = self.time_mlp(time) unet_stack = []for down1, down2, downsample in self.downs:x = down1(x, t)unet_stack.append(x)x = down2(x, t)unet_stack.append(x)x = downsample(x) x = self.mid_block1(x, t)x = self.mid_block2(x, t) for up1, up2, upsample in self.ups:x = torch.cat((x, unet_stack.pop()), dim=1)x = up1(x, t)x = torch.cat((x, unet_stack.pop()), dim=1)x = up2(x, t)x = upsample(x) x = torch.cat((x, r), dim=1)x = self.final_res_block(x, t) return self.final_conv(x)
扩散的代码实现
最后我们介绍一下扩散是如何实现的。由于我们已经介绍了用于正向、逆向和采样过程的所有数学理论,所里这里将重点介绍代码。
class DiffusionModel(nn.Module):SCHEDULER_MAPPING = {"linear": linear_beta_schedule,"cosine": cosine_beta_schedule,"sigmoid": sigmoid_beta_schedule,} def __init__(self,model: nn.Module,image_size: int,*,beta_scheduler: str = "linear",timesteps: int = 1000,schedule_fn_kwargs: dict | None = None,auto_normalize: bool = True,) -> None:super().__init__()self.model = model self.channels = self.model.channelsself.image_size = image_size self.beta_scheduler_fn = self.SCHEDULER_MAPPING.get(beta_scheduler)if self.beta_scheduler_fn is None:raise ValueError(f"unknown beta schedule {beta_scheduler}") if schedule_fn_kwargs is None:schedule_fn_kwargs = {} betas = self.beta_scheduler_fn(timesteps, **schedule_fn_kwargs)alphas = 1.0 - betasalphas_cumprod = torch.cumprod(alphas, dim=0)alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)posterior_variance = (betas * (1.0 - alphas_cumprod_prev) / (1.0 - alphas_cumprod)) register_buffer = lambda name, val: self.register_buffer(name, val.to(torch.float32)) register_buffer("betas", betas)register_buffer("alphas_cumprod", alphas_cumprod)register_buffer("alphas_cumprod_prev", alphas_cumprod_prev)register_buffer("sqrt_recip_alphas", torch.sqrt(1.0 / alphas))register_buffer("sqrt_alphas_cumprod", torch.sqrt(alphas_cumprod))register_buffer("sqrt_one_minus_alphas_cumprod", torch.sqrt(1.0 - alphas_cumprod))register_buffer("posterior_variance", posterior_variance) timesteps, *_ = betas.shapeself.num_timesteps = int(timesteps) self.sampling_timesteps = timesteps self.normalize = normalize_to_neg_one_to_one if auto_normalize else identityself.unnormalize = unnormalize_to_zero_to_one if auto_normalize else identity @torch.inference_mode()def p_sample(self, x: torch.Tensor, timestamp: int) -> torch.Tensor:b, *_, device = *x.shape, x.devicebatched_timestamps = torch.full((b,), timestamp, device=device, dtype=torch.long) preds = self.model(x, batched_timestamps) betas_t = extract(self.betas, batched_timestamps, x.shape)sqrt_recip_alphas_t = extract(self.sqrt_recip_alphas, batched_timestamps, x.shape)sqrt_one_minus_alphas_cumprod_t = extract(self.sqrt_one_minus_alphas_cumprod, batched_timestamps, x.shape) predicted_mean = sqrt_recip_alphas_t * (x - betas_t * preds / sqrt_one_minus_alphas_cumprod_t) if timestamp == 0:return predicted_meanelse:posterior_variance = extract(self.posterior_variance, batched_timestamps, x.shape)noise = torch.randn_like(x)return predicted_mean + torch.sqrt(posterior_variance) * noise @torch.inference_mode()def p_sample_loop(self, shape: tuple, return_all_timesteps: bool = False) -> torch.Tensor:batch, device = shape[0], "mps" img = torch.randn(shape, device=device)# This cause me a RunTimeError on MPS device due to MPS back out of memory# No ideas how to resolve it at this point # imgs = [img] for t in tqdm(reversed(range(0, self.num_timesteps)), total=self.num_timesteps):img = self.p_sample(img, t)# imgs.append(img) ret = img # if not return_all_timesteps else torch.stack(imgs, dim=1) ret = self.unnormalize(ret)return ret def sample(self, batch_size: int = 16, return_all_timesteps: bool = False) -> torch.Tensor:shape = (batch_size, self.channels, self.image_size, self.image_size)return self.p_sample_loop(shape, return_all_timesteps=return_all_timesteps) def q_sample(self, x_start: torch.Tensor, t: int, noise: torch.Tensor = None) -> torch.Tensor:if noise is None:noise = torch.randn_like(x_start) sqrt_alphas_cumprod_t = extract(self.sqrt_alphas_cumprod, t, x_start.shape)sqrt_one_minus_alphas_cumprod_t = extract(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape) return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise def p_loss(self,x_start: torch.Tensor,t: int,noise: torch.Tensor = None,loss_type: str = "l2",) -> torch.Tensor:if noise is None:noise = torch.randn_like(x_start)x_noised = self.q_sample(x_start, t, noise=noise)predicted_noise = self.model(x_noised, t) if loss_type == "l2":loss = F.mse_loss(noise, predicted_noise)elif loss_type == "l1":loss = F.l1_loss(noise, predicted_noise)else:raise ValueError(f"unknown loss type {loss_type}")return loss def forward(self, x: torch.Tensor) -> torch.Tensor:b, c, h, w, device, img_size = *x.shape, x.device, self.image_sizeassert h == w == img_size, f"image size must be {img_size}" timestamp = torch.randint(0, self.num_timesteps, (1,)).long().to(device)x = self.normalize(x)return self.p_loss(x, timestamp)扩散过程是训练部分的模型。它打开了一个采样接口,允许我们使用已经训练好的模型生成样本。
训练的要点总结
对于训练部分,我们设置了37,000步的训练,每步16个批次。由于GPU内存分配限制,图像大小被限制为128x128。使用指数移动平均(EMA)模型权重每1000步生成样本以平滑采样,并保存模型版本。
在最初的1000步训练中,模型开始捕捉一些特征,但仍然错过了某些区域。在10000步左右,这个模型开始产生有希望的结果,进步变得更加明显。在3万步的最后,结果的质量显著提高,但仍然存在黑色图像。这只是因为模型没有足够的样本种类,真实图像的数据分布并没有完全映射到高斯分布。

有了最终的模型权重,我们可以生成一些图片。尽管由于128x128的尺寸限制,图像质量受到限制,但该模型的表现还是不错的。

注:本文使用的数据集是森林地形的卫星图片,具体获取方式请参考源代码中的ETL部分。
总结
我们已经完整的介绍了有关扩散模型的必要知识,并且使用Pytorch进行了完整的实现,本文的代码:
https://github.com/Camaltra/this-is-not-real-aerial-imagery/
위 내용은 PyTorch를 사용하여 노이즈 제거 확산 모델 구현의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7456
7456
 15
15
 1375
1375
 52
52
 77
77
 11
11
 40
40
 19
19
 14
14
 9
9
 iFlytek: Huawei의 Ascend 910B의 기능은 기본적으로 Nvidia의 A100과 비슷하며, 우리 나라의 일반 인공 지능을 위한 새로운 기반을 만들기 위해 협력하고 있습니다.
Oct 22, 2023 pm 06:13 PM
iFlytek: Huawei의 Ascend 910B의 기능은 기본적으로 Nvidia의 A100과 비슷하며, 우리 나라의 일반 인공 지능을 위한 새로운 기반을 만들기 위해 협력하고 있습니다.
Oct 22, 2023 pm 06:13 PM
이 사이트는 10월 22일에 올해 3분기에 iFlytek이 전년 대비 81.86% 감소한 2,579만 위안의 순이익을 달성했다고 보도했습니다. 전년 대비 76.36% 감소했습니다. iFlytek 부사장 Jiang Tao는 3분기 실적 보고에서 iFlytek이 2023년 초 Huawei Shengteng과 특별 연구 프로젝트를 시작했으며 Huawei와 고성능 연산자 라이브러리를 공동 개발하여 중국 일반 인공 지능의 새로운 기반을 마련했다고 밝혔습니다. 이 아키텍처는 독립적인 혁신적인 소프트웨어 및 하드웨어를 기반으로 합니다. 그는 Huawei Ascend 910B의 현재 기능이 기본적으로 Nvidia의 A100과 비슷하다고 지적했습니다. 다가오는 iFlytek 1024 글로벌 개발자 페스티벌에서 iFlytek과 Huawei는 인공 지능 컴퓨팅 기반에 대한 추가 공동 발표를 할 예정입니다. 그는 또한 다음과 같이 언급했습니다.
 PyCharm과 PyTorch의 완벽한 조합: 자세한 설치 및 구성 단계
Feb 21, 2024 pm 12:00 PM
PyCharm과 PyTorch의 완벽한 조합: 자세한 설치 및 구성 단계
Feb 21, 2024 pm 12:00 PM
PyCharm은 강력한 통합 개발 환경(IDE)이고, PyTorch는 딥 러닝 분야에서 인기 있는 오픈 소스 프레임워크입니다. 머신러닝과 딥러닝 분야에서 PyCharm과 PyTorch를 개발에 활용하면 개발 효율성과 코드 품질을 크게 향상시킬 수 있습니다. 이 기사에서는 PyCharm에서 PyTorch를 설치 및 구성하는 방법을 자세히 소개하고 독자가 이 두 가지의 강력한 기능을 더 잘 활용할 수 있도록 특정 코드 예제를 첨부합니다. 1단계: PyCharm 및 Python 설치
 자연어 생성 작업의 5가지 샘플링 방법 및 Pytorch 코드 구현 소개
Feb 20, 2024 am 08:50 AM
자연어 생성 작업의 5가지 샘플링 방법 및 Pytorch 코드 구현 소개
Feb 20, 2024 am 08:50 AM
자연어 생성 작업에서 샘플링 방법은 생성 모델에서 텍스트 출력을 얻는 기술입니다. 이 기사에서는 5가지 일반적인 방법을 논의하고 PyTorch를 사용하여 구현합니다. 1. GreedyDecoding 그리디 디코딩에서는 생성 모델이 시간 단위로 입력 시퀀스를 기반으로 출력 시퀀스의 단어를 예측합니다. 각 시간 단계에서 모델은 각 단어의 조건부 확률 분포를 계산한 다음, 현재 시간 단계의 출력으로 조건부 확률이 가장 높은 단어를 선택합니다. 이 단어는 다음 시간 단계의 입력이 되며 지정된 길이의 시퀀스 또는 특수 종료 표시와 같은 일부 종료 조건이 충족될 때까지 생성 프로세스가 계속됩니다. GreedyDecoding의 특징은 매번 현재 조건부 확률이 가장 좋다는 것입니다.
 PyTorch를 사용하여 노이즈 제거 확산 모델 구현
Jan 14, 2024 pm 10:33 PM
PyTorch를 사용하여 노이즈 제거 확산 모델 구현
Jan 14, 2024 pm 10:33 PM
DDPM(Denoising Diffusion Probabilistic Model)의 작동 원리를 자세히 이해하기 전에 먼저 DDPM의 기초 연구 중 하나인 생성 인공 지능(Generative Artificial Intelligence)의 개발에 대해 먼저 이해해 보겠습니다. VAEVAE는 인코더, 확률적 잠재 공간 및 디코더를 사용합니다. 훈련 중에 인코더는 각 이미지의 평균과 분산을 예측하고 가우스 분포에서 이러한 값을 샘플링합니다. 샘플링 결과는 디코더로 전달되어 입력 이미지를 출력 이미지와 유사한 형태로 변환합니다. KL 발산은 손실을 계산하는 데 사용됩니다. VAE의 중요한 장점은 다양한 이미지를 생성할 수 있다는 것입니다. 샘플링 단계에서는 가우스 분포에서 직접 샘플링하고 디코더를 통해 새로운 이미지를 생성할 수 있습니다. GAN은 단 1년 만에 VAE(변형 자동 인코더) 분야에서 큰 발전을 이루었습니다.
 PyTorch와 함께 PyCharm을 설치하는 방법에 대한 튜토리얼
Feb 24, 2024 am 10:09 AM
PyTorch와 함께 PyCharm을 설치하는 방법에 대한 튜토리얼
Feb 24, 2024 am 10:09 AM
강력한 딥 러닝 프레임워크인 PyTorch는 다양한 머신 러닝 프로젝트에서 널리 사용됩니다. 강력한 Python 통합 개발 환경인 PyCharm은 딥 러닝 작업을 구현할 때에도 훌륭한 지원을 제공할 수 있습니다. 이 기사에서는 PyCharm에 PyTorch를 설치하는 방법을 자세히 소개하고 독자가 딥 러닝 작업에 PyTorch를 사용하여 빠르게 시작할 수 있도록 구체적인 코드 예제를 제공합니다. 1단계: PyCharm 설치 먼저 다음 사항을 확인해야 합니다.
 PHP와 PyTorch를 사용한 딥 러닝
Jun 19, 2023 pm 02:43 PM
PHP와 PyTorch를 사용한 딥 러닝
Jun 19, 2023 pm 02:43 PM
딥러닝은 인공지능 분야에서 중요한 분야로 최근 몇 년간 점점 더 많은 주목을 받고 있습니다. 딥 러닝 연구 및 응용을 수행하려면 이를 달성하는 데 도움이 되는 일부 딥 러닝 프레임워크를 사용해야 하는 경우가 많습니다. 이번 글에서는 딥러닝에 PHP와 PyTorch를 활용하는 방법을 소개하겠습니다. 1. PyTorch란 무엇입니까? PyTorch는 Facebook에서 개발한 오픈 소스 머신 러닝 프레임워크로, 딥 러닝 모델을 빠르게 생성하고 훈련하는 데 도움이 됩니다. 파이톡
 너무 빨라요! 10줄 미만의 코드로 단 몇 분 만에 비디오 음성을 텍스트로 인식합니다.
Feb 27, 2024 pm 01:55 PM
너무 빨라요! 10줄 미만의 코드로 단 몇 분 만에 비디오 음성을 텍스트로 인식합니다.
Feb 27, 2024 pm 01:55 PM
안녕하세요 여러분, 저는 Kite입니다. 2년 전에는 오디오 및 비디오 파일을 텍스트 콘텐츠로 변환하는 작업이 어려웠지만 이제는 단 몇 분만에 쉽게 해결할 수 있습니다. 훈련 데이터를 얻기 위해 일부 회사에서는 Douyin, Kuaishou 등 짧은 비디오 플랫폼에서 비디오를 완전히 크롤링한 다음 비디오에서 오디오를 추출하고 이를 텍스트 형식으로 변환하여 빅데이터 모델의 훈련 코퍼스로 사용했다고 합니다. . 비디오 또는 오디오 파일을 텍스트로 변환해야 하는 경우 현재 제공되는 이 오픈 소스 솔루션을 사용해 볼 수 있습니다. 예를 들어, 영화나 TV 프로그램의 대화가 나오는 특정 시점을 검색할 수 있습니다. 더 이상 고민하지 않고 요점을 살펴보겠습니다. Whisper는 OpenAI의 오픈 소스 Whisper입니다. 물론 Python으로 작성되었습니다. 몇 가지 간단한 설치 패키지만 있으면 됩니다.
 pycharm에 pytorch를 설치하는 방법
Dec 08, 2023 pm 03:05 PM
pycharm에 pytorch를 설치하는 방법
Dec 08, 2023 pm 03:05 PM
설치 단계: 1. PyCharm을 열고 새 Python 프로젝트를 생성합니다. 2. PyCharm 하단 상태 표시줄에서 "터미널" 아이콘을 클릭하여 터미널 창을 엽니다. 3. 터미널 창에서 pip 명령을 사용하여 PyTorch를 설치합니다. , 시스템 및 요구 사항에 따라 다양한 설치 방법을 선택할 수 있습니다. 4. 설치가 완료된 후 PyCharm에 코드를 작성하고 PyTorch 라이브러리를 가져와 사용할 수 있습니다.




