소프트 및 하드 제약 조건 하의 궤적 생성: 이론 및 코드에 대한 자세한 설명
이 프로젝트의 코드:
github.com/liangwq/robot_motion_planing
궤적 제약의 소프트 및 하드 제약
이전 기사에서는 이미 궤적 제약의 본질이 제약된 궤적 피팅을 수행하는 것이라고 소개했습니다. 입력은 웨이포인트 목록이며, 제약에는 하드 제약과 소프트 제약의 두 가지 유형이 있습니다. 소위 하드 제약은 비용 함수의 수학적 형태에 해당하고 하드 제약은 최적화 가을의 제약 조건에 해당합니다. 물리적인 의미에 따라, 로봇이 걸을 수 있는 안전한 궤적을 얻기 위해 다음과 같은 것들이 있습니다:
- 비용 함수를 통해 장애물로부터 궤적을 밀어냅니다.
- 장애물 사이에 걸을 수 있는 볼록 선체 복도를 제공하고 사용합니다. 로봇 궤적은 볼록한 선체 복도를 따라 걸어야 합니다

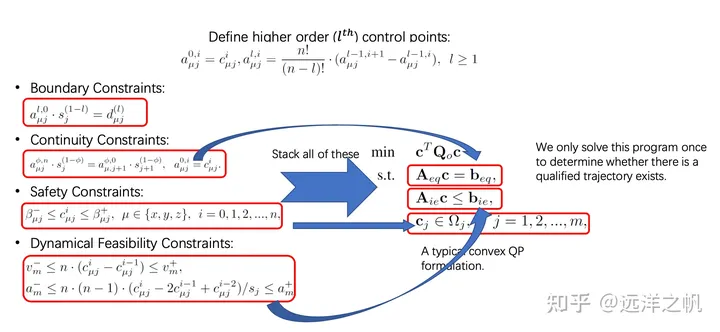
위 그림은 소프트 및 하드 제약 하에서 베지어 곡선 피팅을 해결하기 위한 수학적 프레임워크와 다양한 제약 조건을 수학적 솔루션으로 변환하는 방법을 보여줍니다. 비용 함수(소프트 제약 조건) 또는 해결해야 할 제약 조건(소프트 제약 조건). image.png
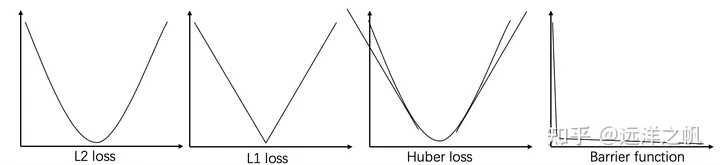
위는 일반적으로 사용되는 비용 함수 제약 조건의 여러 표현의 예입니다. image.png
베지어 곡선 피팅 궤적
이전 기사에서는 베지어 곡선 피팅의 다양한 장점을 소개했습니다:
- 끝점 보간. 베지어 곡선은 항상 첫 번째 제어점에서 시작하고 마지막 제어점에서 끝나며 다른 제어점을 통과하지 않습니다.
- 볼록한 껍질. 베지어 곡선( )은 일련의 제어점으로 구성되며 모든 제어점에 의해 정의된 볼록 껍질 내에 완전히 제한됩니다.
- 속도 곡선. 베지어 곡선( )의 미분 곡선 ′( )을 속도 곡선이라 부르는데, 이는 제어점에 의해 정의되는 베지어 곡선이기도 하며, 여기서 제어점은 ∙( +1− )이고, 여기서 차수는 이다.
- 고정된 시간 간격. 베지어 곡선은 항상 [0,1]에 정의됩니다.
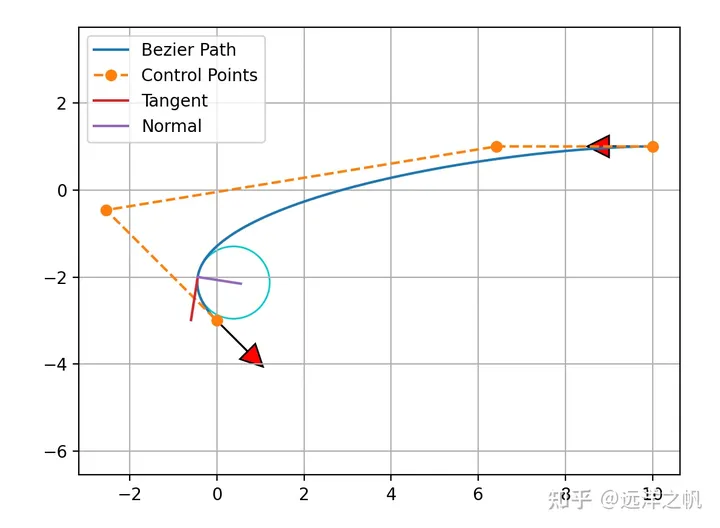
그림1. 궤적의 한 부분에 베지어 곡선이 맞춰져 있습니다. image.png
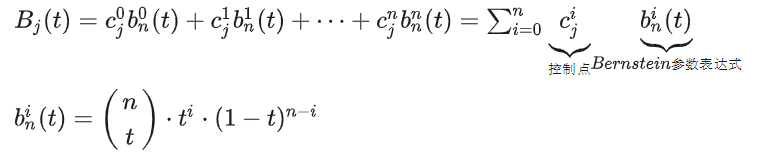
위의 두 표현식에 해당하는 코드는 다음과 같이 구현됩니다.
def bernstein_poly(n, i, t):"""Bernstein polynom.:param n: (int) polynom degree:param i: (int):param t: (float):return: (float)"""return scipy.special.comb(n, i) * t ** i * (1 - t) ** (n - i)def bezier(t, control_points):"""Return one point on the bezier curve.:param t: (float) number in [0, 1]:param control_points: (numpy array):return: (numpy array) Coordinates of the point"""n = len(control_points) - 1return np.sum([bernstein_poly(n, i, t) * control_points[i] for i in range(n + 1)], axis=0)
베지어 곡선을 사용하여 표현하려면 곡선 섹션은 위에 나와 있습니다. 표현식과 코드 구현이 방해가 되면서 이제 누락된 것은 제어점을 가져오고 베지어 곡선 표현식을 사용하여 필요한 점의 좌표를 계산합니다. 주어진 끝점과 끝점에 그려집니다. 다음 코드는 곡선을 그리기 위해 4개의 제어점과 6개의 제어점의 베지어 곡선 구현을 제공하며 170개의 온라인 점을 계산해야 합니다. 코드는 다음과 같습니다.
def calc_4points_bezier_path(sx, sy, syaw, ex, ey, eyaw, offset):"""Compute control points and path given start and end position.:param sx: (float) x-coordinate of the starting point:param sy: (float) y-coordinate of the starting point:param syaw: (float) yaw angle at start:param ex: (float) x-coordinate of the ending point:param ey: (float) y-coordinate of the ending point:param eyaw: (float) yaw angle at the end:param offset: (float):return: (numpy array, numpy array)"""dist = np.hypot(sx - ex, sy - ey) / offsetcontrol_points = np.array([[sx, sy], [sx + dist * np.cos(syaw), sy + dist * np.sin(syaw)], [ex - dist * np.cos(eyaw), ey - dist * np.sin(eyaw)], [ex, ey]])path = calc_bezier_path(control_points, n_points=170)return path, control_pointsdef calc_6points_bezier_path(sx, sy, syaw, ex, ey, eyaw, offset):"""Compute control points and path given start and end position.:param sx: (float) x-coordinate of the starting point:param sy: (float) y-coordinate of the starting point:param syaw: (float) yaw angle at start:param ex: (float) x-coordinate of the ending point:param ey: (float) y-coordinate of the ending point:param eyaw: (float) yaw angle at the end:param offset: (float):return: (numpy array, numpy array)"""dist = np.hypot(sx - ex, sy - ey) * offsetcontrol_points = np.array([[sx, sy], [sx + 0.25 * dist * np.cos(syaw), sy + 0.25 * dist * np.sin(syaw)], [sx + 0.40 * dist * np.cos(syaw), sy + 0.40 * dist * np.sin(syaw)], [ex - 0.40 * dist * np.cos(eyaw), ey - 0.40 * dist * np.sin(eyaw)], [ex - 0.25 * dist * np.cos(eyaw), ey - 0.25 * dist * np.sin(eyaw)], [ex, ey]])path = calc_bezier_path(control_points, n_points=170)return path, control_pointsdef calc_bezier_path(control_points, n_points=100):"""Compute bezier path (trajectory) given control points.:param control_points: (numpy array):param n_points: (int) number of points in the trajectory:return: (numpy array)"""traj = []for t in np.linspace(0, 1, n_points):traj.append(bezier(t, control_points))return np.array(traj)
베지어 곡선의 피팅 방법에서 다음으로 해야 할 일은 여러 개의 베지어 곡선을 생성하여 궤적을 합성하는 방법이며 비용 함수 방법(소프트 제약 조건)을 거쳐야 합니다. 부드러운 궤적 곡선을 생성하려면 지정된 점 + 공식을 통과해야 합니다. 점 연결은 연속적(하드 제약 조건)이어야 합니다.
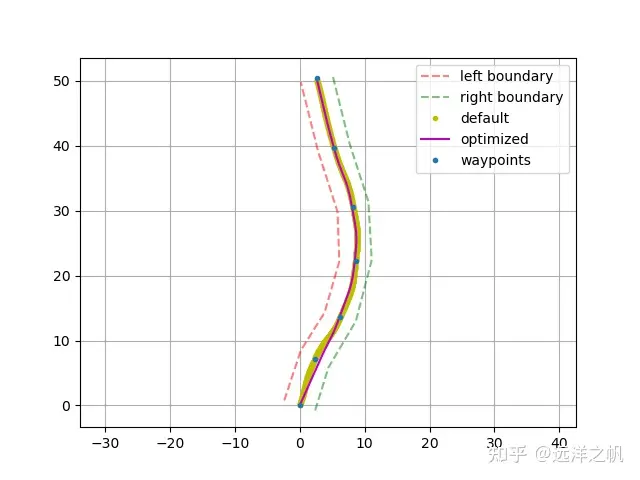
Fig2. 장애물 없음, 결합 궤적을 통한 원활한 최적화 Figure_1.png
다중 세그먼트 베지어 곡선 생성 코드는 실제로 여러 개의 웨이포인트가 주어지면 원리는 매우 간단합니다. 세그먼트 베지저 곡선의 코드는 다음과 같습니다.
# Bezier path one as per the approach suggested in# https://users.soe.ucsc.edu/~elkaim/Documents/camera_WCECS2008_IEEE_ICIAR_58.pdfdef cubic_bezier_path(self, ax, ay):dyaw, _ = self.calc_yaw_curvature(ax, ay)cx = []cy = []ayaw = dyaw.copy()for n in range(1, len(ax)-1):yaw = 0.5*(dyaw[n] + dyaw[n-1])ayaw[n] = yawlast_ax = ax[0]last_ay = ay[0]last_ayaw = ayaw[0]# for n waypoints, there are n-1 bezier curvesfor i in range(len(ax)-1):path, ctr_points = calc_4points_bezier_path(last_ax, last_ay, ayaw[i], ax[i+1], ay[i+1], ayaw[i+1], 2.0)cx = np.concatenate((cx, path.T[0][:-2]))cy = np.concatenate((cy, path.T[1][:-2]))cyaw, k = self.calc_yaw_curvature(cx, cy)last_ax = path.T[0][-1]last_ay = path.T[1][-1]return cx, cy
비용 함수 계산에는 곡률 비용 + 편차 비용 + 거리 비용 + 연속성 비용뿐만 아니라 경계 조건, 궤적이 튜브 내에 있어야 한다는 부등식 제약 조건 및 문제가 포함됩니다. 최적화 솔루션. 구체적인 코드는 다음과 같이 구현됩니다.
# Objective function of cost to be minimizeddef cubic_objective_func(self, deviation):ax = self.waypoints.x.copy()ay = self.waypoints.y.copy()for n in range(0, len(deviation)):ax[n+1] -= deviation[n]*np.sin(self.waypoints.yaw[n+1])ay[n+1] += deviation[n]*np.cos(self.waypoints.yaw[n+1])bx, by = self.cubic_bezier_path(ax, ay)yaw, k = self.calc_yaw_curvature(bx, by)# cost of curvature continuityt = np.zeros((len(k)))dk = self.calc_d(t, k)absolute_dk = np.absolute(dk)continuity_cost = 10.0 * np.mean(absolute_dk)# curvature costabsolute_k = np.absolute(k)curvature_cost = 14.0 * np.mean(absolute_k)# cost of deviation from input waypointsabsolute_dev = np.absolute(deviation)deviation_cost = 1.0 * np.mean(absolute_dev)distance_cost = 0.5 * self.calc_path_dist(bx, by)return curvature_cost + deviation_cost + distance_cost + continuity_cost# Minimize objective function using scipy optimize minimizedef optimize_min_cubic(self):print("Attempting optimization minima")initial_guess = [0, 0, 0, 0, 0]bnds = ((-self.bound, self.bound), (-self.bound, self.bound), (-self.bound, self.bound), (-self.bound, self.bound), (-self.bound, self.bound))result = optimize.minimize(self.cubic_objective_func, initial_guess, bounds=bnds)ax = self.waypoints.x.copy()ay = self.waypoints.y.copy()if result.success:print("optimized true")deviation = result.xfor n in range(0, len(deviation)):ax[n+1] -= deviation[n]*np.sin(self.waypoints.yaw[n+1])ay[n+1] += deviation[n]*np.cos(self.waypoints.yaw[n+1])x, y = self.cubic_bezier_path(ax, ay)yaw, k = self.calc_yaw_curvature(x, y)self.optimized_path = Path(x, y, yaw, k)else:print("optimization failure, defaulting")exit()장애물이 있는 베지어 곡선 궤적은 장애물이 있는 장면을
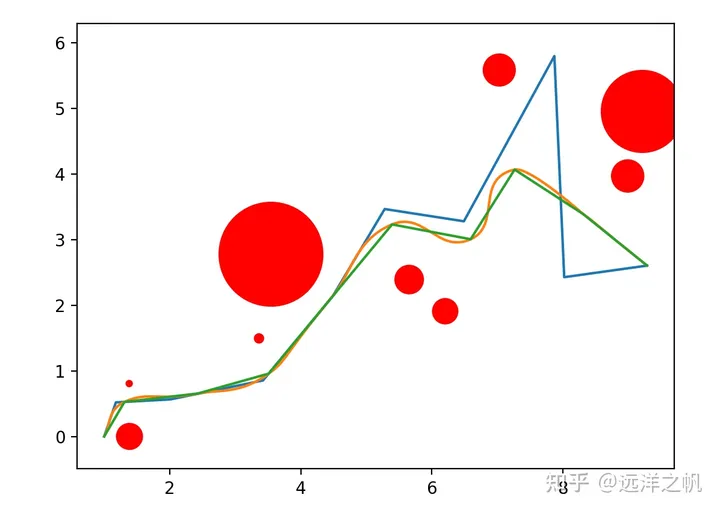
생성하고 비용 함수는 생성된 곡선을 장애물로부터 멀리 유지하는 데 사용됩니다. 안전하게 걸을 수 있는 궤적을 얻기 위한 구체적인 코드 구현은 다음과 같습니다. Optimizer_k의 람다 함수 f는 궤도가 장애물 근처를 통과할 때의 비용을 해결하는 것입니다. 페널티1과 페널티2는 장애물 근처를 통과하는 곡선의 특정 비용 값을 찾는 것입니다.
b.arc_len(granuality=10)+B. arc_len(granuality= 10)+m_k + 페널티1 + 페널티2는 궤적의 전체 비용입니다. for 루프 부분은 scipy의 최적화 및 최소화를 사용하여 궤적을 해결합니다.
def optimizer_k(cd, k, path, i, obs, curve_penalty_multiplier, curve_penalty_divider, curve_penalty_obst):"""Bezier curve optimizer that optimizes the curvature and path length by changing the distance of p1 and p2 from points p0 and p3, respectively. """p_tmp = copy.deepcopy(path)if i+3 > len(path)-1:b = CubicBezier()b.p0 = p_tmp[i]x, y = calc_p1(p_tmp[i], p_tmp[i + 1], p_tmp[i - 1], i, cd[0])b.p1 = Point(x, y)x, y = calc_p2(p_tmp[i-1], p_tmp[i + 0], p_tmp[i + 1], i, cd[1])b.p2 = Point(x, y)b.p3 = p_tmp[i + 1]B = CubicBezier()else:b = CubicBezier()b.p0 = p_tmp[i]x, y = calc_p1(p_tmp[i],p_tmp[i+1],p_tmp[i-1], i, cd[0])b.p1 = Point(x, y)x, y = calc_p2(p_tmp[i],p_tmp[i+1],p_tmp[i+2], i, cd[1])b.p2 = Point(x, y)b.p3 = p_tmp[i + 1]B = CubicBezier()B.p0 = p_tmp[i]x, y = calc_p1(p_tmp[i+1], p_tmp[i + 2], p_tmp[i], i, 10)B.p1 = Point(x, y)x, y = calc_p2(p_tmp[i+1], p_tmp[i + 2], p_tmp[i + 3], i, 10)B.p2 = Point(x, y)B.p3 = p_tmp[i + 1]m_k = b.max_k()if m_k>k:m_k= m_k*curve_penalty_multiplierelse:m_k = m_k/curve_penalty_dividerf = lambda x, y: max(math.sqrt((x[0] - y[0].x) ** 2 + (x[1] - y[0].y) ** 2) * curve_penalty_obst, 10) if math.sqrt((x[0] - y[0].x) ** 2 + (x[1] - y[0].y) ** 2) <h2 id="span-带飞行走廊的Bezier轨迹生成-span"><span>带飞行走廊的Bezier轨迹生成</span></h2><p>得益于贝赛尔曲线拟合的优势,如果我们可以让机器人可行走的轨迹转成多个有重叠区域的凸多面体,那么轨迹完全位于飞行走廊内。</p><p style="text-align:center;"><img src="/static/imghw/default1.png" data-src="https://img.php.cn/upload/article/000/887/227/170524425539093.png" class="lazy" alt="소프트 및 하드 제약 조건 하의 궤적 생성: 이론 및 코드에 대한 자세한 설명"></p><p>image.png</p>
- 飞行走廊由凸多边形组成。
- 每个立方体对应于一段贝塞尔曲线。
- 此曲线的控制点被强制限制在多边形内部。
- 轨迹完全位于所有点的凸包内。
如何通过把障碍物地图生成可行凸包走廊
生成凸包走廊的方法目前有以下三大类的方法:
平行凸簇膨胀方法
从栅格地图出发,利用最小凸集生成算法,完成凸多面体的生成。其算法的思想是首先获得一个凸集,再沿着凸集的表面进行扩张,扩张之后再进行凸集检测,判断新扩张的集合是否保持为凸。一直扩张到不能再扩张为止,再提取凸集的边缘点,利用快速凸集生成算法,生成凸多面体。该算法的好处在于可以利用这种扩张的思路,将安全的多面体的体积尽可能的充满整个空间,因此获得的安全通道更大。但其也具有一定的缺点,就是计算量比较大,计算所需要的时间比较长,为了解决这个问题,在该文章中,又提出了采用GPU加速的方法,来加速计算。
基于凸分解的安全通道生成
基于凸分解的安全通道生成方法由四个步骤完成安全通道的生成,分别为:找到椭球、找到多面体、边界框、收缩。
半定规划的迭代区域膨胀
为了获取多面体,这个方法首先构造一个初始椭球,由一个以选定点为中心的单位球组成。然后,遍历障碍物,为每个障碍物生成一个超平面,该超平面与障碍物相切并将其与椭球分开。再次,这些超平面定义了一组线性约束,它们的交集是一个多面体。然后,可以在那个多面体中找到一个最大的椭球,使用这个椭球来定义一组新的分离超平面,从而定义一个新的多面体。选择生成分离超平面的方法,这样椭圆体的体积在迭代之间永远不会减少。可以重复这个过程,直到椭圆体的增长率低于某个阈值,此时我们返回多面体和内接椭圆体。这个方法具有迭代的思想,并且具有收敛判断的标准,算法的收敛快慢和初始椭球具有很大的关系。
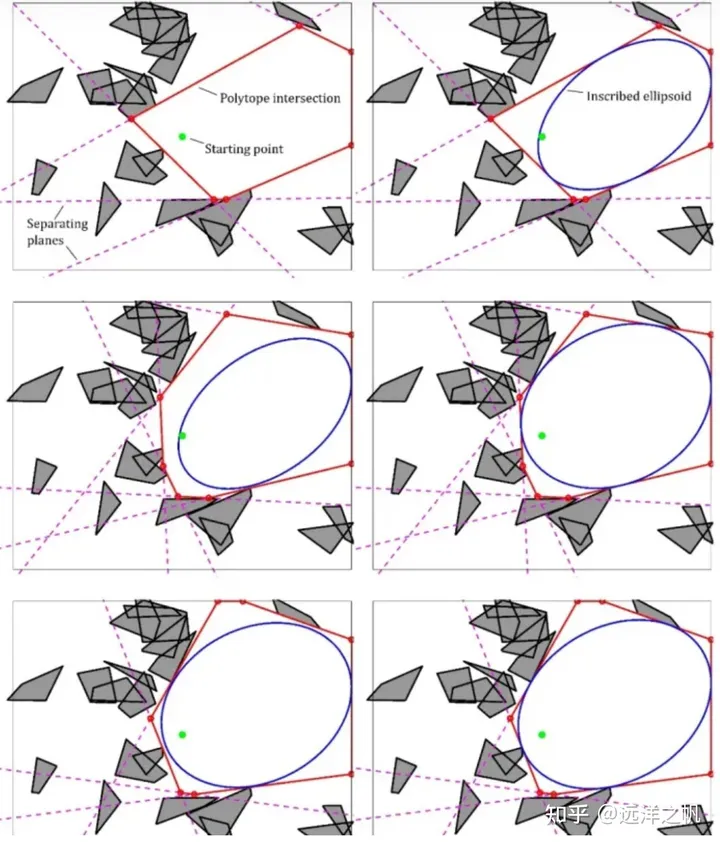
Fig3.半定规划的迭代区域膨胀。每一行即为一次迭代操作,直到椭圆体的增长率低于阈值。image.png
这篇文章介绍的是“半定规划的迭代区域膨胀”方法,具体代码实现如下:
# 根据输入路径对空间进行凸分解def decomp(self, line_points: list[np.array], obs_points: list[np.array], visualize=True):# 最终结果decomp_polygons = list()# 构建输入障碍物点的kdtreeobs_kdtree = KDTree(obs_points)# 进行空间分解for i in range(len(line_points) - 1):# 得到当前线段pf, pr = line_points[i], line_points[i + 1]print(pf)print(pr)# 构建初始多面体init_polygon = self.initPolygon(pf, pr)print(init_polygon.getInterPoints())print(init_polygon.getVerticals())# 过滤障碍物点candidate_obs_point_indexes = obs_kdtree.query_ball_point((pf + pr) / 2, np.linalg.norm([np.linalg.norm(pr - pf) / 2 + self.consider_range_, self.consider_range_]))local_obs_points = list()for index in candidate_obs_point_indexes:if init_polygon.inside(obs_points[index]):local_obs_points.append(obs_points[index])# 得到初始椭圆ellipse = self.findEllipse(pf, pr, local_obs_points)# 根据初始椭圆构建多面体polygon = self.findPolygon(ellipse, init_polygon, local_obs_points)# 进行保存decomp_polygons.append(polygon)if visualize:# 进行可视化plt.figure()# 绘制路径段plt.plot([pf[1], pr[1]], [pf[0], pr[0]], color="red")# 绘制初始多面体verticals = init_polygon.getVerticals()# 绘制多面体顶点plt.plot([v[1] for v in verticals] + [verticals[0][1]], [v[0] for v in verticals] + [verticals[0][0]], color="blue", linestyle="--")# 绘制障碍物点plt.scatter([p[1] for p in local_obs_points], [p[0] for p in local_obs_points], marker="o")# 绘制椭圆ellipse_x, ellipse_y = list(), list()for theta in np.linspace(-np.pi, np.pi, 1000):raw_point = np.array([np.cos(theta), np.sin(theta)])ellipse_point = np.dot(ellipse.C_, raw_point) + ellipse.d_ellipse_x.append(ellipse_point[0])ellipse_y.append(ellipse_point[1])plt.plot(ellipse_y, ellipse_x, color="orange")# 绘制最终多面体# 得到多面体顶点verticals = polygon.getVerticals()# 绘制多面体顶点plt.plot([v[1] for v in verticals] + [verticals[0][1]], [v[0] for v in verticals] + [verticals[0][0]], color="green")plt.show()return decomp_polygons# 构建初始多面体def initPolygon(self, pf: np.array, pr: np.array) -> Polygon:# 记录多面体的平面polygon_planes = list()# 得到线段方向向量dire = self.normalize(pr - pf)# 得到线段法向量dire_h = np.array([dire[1], -dire[0]])# 得到平行范围p_1 = pf + self.consider_range_ * dire_hp_2 = pf - self.consider_range_ * dire_hpolygon_planes.append(Hyperplane(dire_h, p_1))polygon_planes.append(Hyperplane(-dire_h, p_2))# 得到垂直范围p_3 = pr + self.consider_range_ * direp_4 = pf - self.consider_range_ * direpolygon_planes.append(Hyperplane(dire, p_3))polygon_planes.append(Hyperplane(-dire, p_4))# 构建多面体polygon = Polygon(polygon_planes)return polygon# 得到初始椭圆def findEllipse(self, pf: np.array, pr: np.array, obs_points: list[np.array]) -> Ellipse:# 计算长轴long_axis_value = np.linalg.norm(pr - pf) / 2axes = np.array([long_axis_value, long_axis_value])# 计算旋转rotation = self.vec2Rotation(pr - pf)# 计算初始椭圆C = np.dot(rotation, np.dot(np.array([[axes[0], 0], [0, axes[1]]]), np.transpose(rotation)))d = (pr + pf) / 2ellipse = Ellipse(C, d)# 得到椭圆内的障碍物点inside_obs_points = ellipse.insidePoints(obs_points)# 对椭圆进行调整,使得全部障碍物点都在椭圆外while inside_obs_points:# 得到与椭圆距离最近的点closest_obs_point = ellipse.closestPoint(inside_obs_points)# 将最近点转到椭圆坐标系下closest_obs_point = np.dot(np.transpose(rotation), closest_obs_point - ellipse.d_) # 根据最近点,在椭圆长轴不变的情况下对短轴进行改变,使得,障碍物点在椭圆上if Compare.small(closest_obs_point[0], axes[0]):axes[1] = np.abs(closest_obs_point[1]) / np.sqrt(1 - (closest_obs_point[0] / axes[0]) ** 2)# 更新椭圆ellipse.C_ = np.dot(rotation, np.dot(np.array([[axes[0], 0], [0, axes[1]]]), np.transpose(rotation)))# 更新椭圆内部障碍物inside_obs_points = ellipse.insidePoints(inside_obs_points, include_bound=False)return ellipse# 进行多面体的构建def findPolygon(self, ellipse: Ellipse, init_polygon: Polygon, obs_points: list[np.array]) -> Polygon:# 多面体由多个超平面构成polygon_planes = copy.deepcopy(init_polygon.hyper_planes_)# 初始化范围超平面remain_obs_points = obs_pointswhile remain_obs_points:# 得到与椭圆最近障碍物closest_point = ellipse.closestPoint(remain_obs_points)# 计算该处的切平面的法向量norm_vector = np.dot(np.linalg.inv(ellipse.C_), np.dot(np.linalg.inv(ellipse.C_), (closest_point - ellipse.d_)))norm_vector = self.normalize(norm_vector)# 构建平面hyper_plane = Hyperplane(norm_vector, closest_point)# 保存到多面体平面中polygon_planes.append(hyper_plane)# 去除切平面外部的障碍物new_remain_obs_points = list()for point in remain_obs_points:if Compare.small(hyper_plane.signDist(point), 0):new_remain_obs_points.append(point)remain_obs_points = new_remain_obs_pointspolygon = Polygon(polygon_planes)return polygon
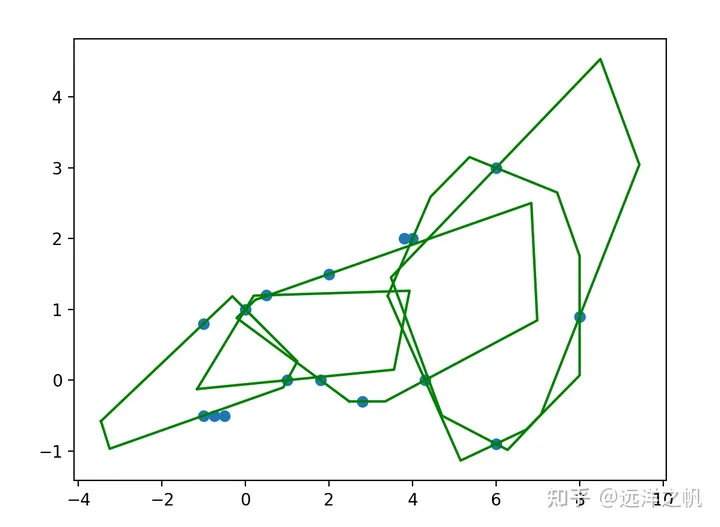
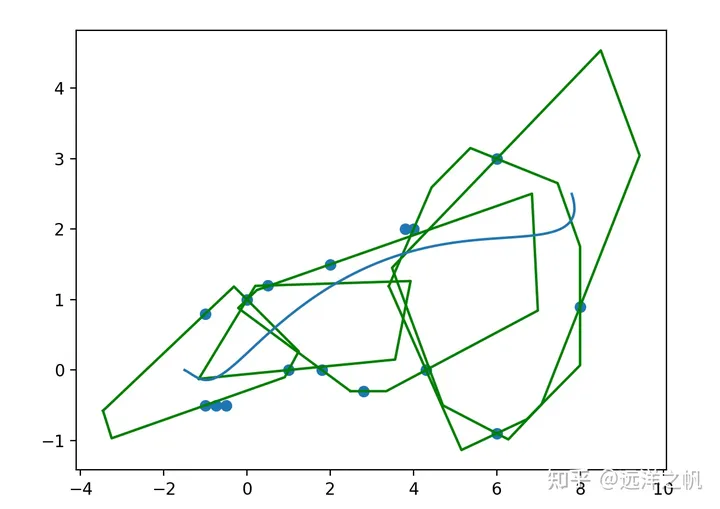
上面图是给定16个障碍物点,必经6个路径点后得到的凸包可行走廊,具体代码如下:
def main():# 路径点line_points = [np.array([-1.5, 0.0]), np.array([0.0, 0.8]), np.array([1.5, 0.3]), np.array([5, 0.6]), np.array([6, 1.2]), np.array([7.6, 2.2])]# 障碍物点obs_points = [np.array([4, 2.0]),np.array([6, 3.0]),np.array([2, 1.5]),np.array([0, 1]),np.array([1, 0]),np.array([1.8, 0]),np.array([3.8, 2]),np.array([0.5, 1.2]),np.array([4.3, 0]),np.array([8, 0.9]),np.array([2.8, -0.3]),np.array([6, -0.9]),np.array([-0.5, -0.5]),np.array([-0.75 ,-0.5]),np.array([-1, -0.5]),np.array([-1, 0.8])]convex_decomp = ConvexDecomp(2)decomp_polygons = convex_decomp.decomp(line_points, obs_points, False)#convex_decomp.decomp(line_points, obs_points,False)plt.figure()# 绘制障碍物点plt.scatter([p[0] for p in obs_points], [p[1] for p in obs_points], marker="o")# 绘制边界for polygon in decomp_polygons:verticals = polygon.getVerticals()# 绘制多面体顶点plt.plot([v[0] for v in verticals] + [verticals[0][0]], [v[1] for v in verticals] + [verticals[0][1]], color="green")#plt.plot(x_samples, y_samples)plt.show()
带凸包走廊求解
带凸包走廊的光滑轨迹生成。前面已经求解得到了可行的凸包走廊,这部分可以做为硬约束作为最优化求解的不等式条件。要求的光滑路径和必须经过点的点,这部分可以把必须经过点作为等式约束,光滑路径可以通过代价函数来实现。这样就可以把带软硬约束的轨迹生成框架各种技能点都用上了。
下面看具体代码实现:
# 进行优化def optimize(self, start_state: np.array, end_state: np.array, line_points: list[np.array], polygons: list[Polygon]):assert(len(line_points) == len(polygons) + 1)# 得到分段数量segment_num = len(polygons)assert(segment_num >= 1)# 计算初始时间分配time_allocations = list()for i in range(segment_num):time_allocations.append(np.linalg.norm(line_points[i+1] - line_points[i]) / self.vel_max_)# 进行优化迭代max_inter = 10cur_iter = 0while cur_iter <h2 id="span-小结-span"><span>小结:</span></h2><p>这篇文章介绍了带软硬约束的轨迹优化算法框架。第一部份介绍了软硬约束对应到最优求解问题数学上如何表示。第二部份介绍了贝赛尔曲线的代码实现,给出了具体的代码实现和讲解;并针对没有障碍物场景只给定waypoint点,生成光滑的Bezier轨迹的朴素求解代码实现。第三部份给出了带障碍物情况下如何做最优化求解,如何通过代价函数的方式来给轨迹施加推力让轨迹远离障碍物的代码实现。第四部分是一个综合性的例子,把软硬约束最优轨迹生成的求解框架做了一个综合呈现。详细的介绍了如何利用障碍物地图生成最大可行区域的凸包走廊,如何利用Bezier曲线的特性给定凸包两点生成路径一定在凸包中;以及如何利用代价行数来保证轨迹的光滑性、安全性,通过等式、不等式约束实现轨迹必须经过哪些点,某个点的运动状态如何。<br>这一系列的文章已经进入结尾的阶段,后面会简单介绍在碰到移动的物体时候单机器人如何处理;以及在多个机器人运行环境如何协同,最后会给出一个Motion Planning的综合实现例子讲解实际环境数据输入、前端规划、后端轨迹生成。至于定位和感知部分的内容后面可以根据情况而定是否在开一个新的系列来讲解介绍,对于更前沿的技术点会跟进论文做些文章分享。<br>最后本系列文章的代码在以下git链接,这部分代码相对零碎主要是配合文章理论来讲的,里面很多片段直接来源于网络整合。后面这可项目会持续维护,把项目代码(应该是c++实现,更体系)、整合进来,根据需要在看看有没必要整合出一个库。</p><p style="text-align:center;"><img src="/static/imghw/default1.png" data-src="https://img.php.cn/upload/article/000/887/227/170524425687764.jpg" class="lazy" alt="소프트 및 하드 제약 조건 하의 궤적 생성: 이론 및 코드에 대한 자세한 설명"></p><p>原文链接:https://mp.weixin.qq.com/s/0EVgYKTxLzUj64L5jzMVug</p>
위 내용은 소프트 및 하드 제약 조건 하의 궤적 생성: 이론 및 코드에 대한 자세한 설명의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

Video Face Swap
완전히 무료인 AI 얼굴 교환 도구를 사용하여 모든 비디오의 얼굴을 쉽게 바꾸세요!

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7658
7658
 15
15
 1393
1393
 52
52
 91
91
 11
11
 73
73
 19
19
 38
38
 113
113
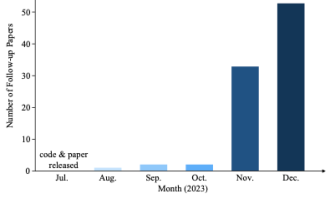 자율주행 분야에서 Gaussian Splatting이 인기를 끌면서 NeRF가 폐기되기 시작한 이유는 무엇입니까?
Jan 17, 2024 pm 02:57 PM
자율주행 분야에서 Gaussian Splatting이 인기를 끌면서 NeRF가 폐기되기 시작한 이유는 무엇입니까?
Jan 17, 2024 pm 02:57 PM
위에 작성됨 및 저자의 개인적인 이해 3DGS(3차원 가우스플래팅)는 최근 몇 년간 명시적 방사선장 및 컴퓨터 그래픽 분야에서 등장한 혁신적인 기술입니다. 이 혁신적인 방법은 수백만 개의 3D 가우스를 사용하는 것이 특징이며, 이는 주로 암시적 좌표 기반 모델을 사용하여 공간 좌표를 픽셀 값에 매핑하는 NeRF(Neural Radiation Field) 방법과 매우 다릅니다. 명시적인 장면 표현과 미분 가능한 렌더링 알고리즘을 갖춘 3DGS는 실시간 렌더링 기능을 보장할 뿐만 아니라 전례 없는 수준의 제어 및 장면 편집 기능을 제공합니다. 이는 3DGS를 차세대 3D 재구성 및 표현을 위한 잠재적인 게임 체인저로 자리매김합니다. 이를 위해 우리는 처음으로 3DGS 분야의 최신 개발 및 관심사에 대한 체계적인 개요를 제공합니다.
 자율주행 시나리오에서 롱테일 문제를 해결하는 방법은 무엇입니까?
Jun 02, 2024 pm 02:44 PM
자율주행 시나리오에서 롱테일 문제를 해결하는 방법은 무엇입니까?
Jun 02, 2024 pm 02:44 PM
어제 인터뷰 도중 롱테일 관련 질문을 해본 적이 있느냐는 질문을 받아서 간략하게 요약해볼까 생각했습니다. 자율주행의 롱테일 문제는 자율주행차의 엣지 케이스, 즉 발생 확률이 낮은 가능한 시나리오를 말한다. 인지된 롱테일 문제는 현재 단일 차량 지능형 자율주행차의 운영 설계 영역을 제한하는 주요 이유 중 하나입니다. 자율주행의 기본 아키텍처와 대부분의 기술적인 문제는 해결되었으며, 나머지 5%의 롱테일 문제는 점차 자율주행 발전을 제한하는 핵심이 되었습니다. 이러한 문제에는 다양한 단편적인 시나리오, 극단적인 상황, 예측할 수 없는 인간 행동이 포함됩니다. 자율 주행에서 엣지 시나리오의 "롱테일"은 자율주행차(AV)의 엣지 케이스를 의미하며 발생 확률이 낮은 가능한 시나리오입니다. 이런 희귀한 사건
 카메라 또는 LiDAR를 선택하시겠습니까? 강력한 3D 객체 감지 달성에 대한 최근 검토
Jan 26, 2024 am 11:18 AM
카메라 또는 LiDAR를 선택하시겠습니까? 강력한 3D 객체 감지 달성에 대한 최근 검토
Jan 26, 2024 am 11:18 AM
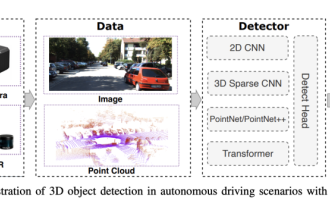
0. 전면 작성&& 자율주행 시스템은 다양한 센서(예: 카메라, 라이더, 레이더 등)를 사용하여 주변 환경을 인식하고 알고리즘과 모델을 사용하는 고급 인식, 의사결정 및 제어 기술에 의존한다는 개인적인 이해 실시간 분석과 의사결정을 위해 이를 통해 차량은 도로 표지판을 인식하고, 다른 차량을 감지 및 추적하며, 보행자 행동을 예측하는 등 복잡한 교통 환경에 안전하게 작동하고 적응할 수 있게 되므로 현재 널리 주목받고 있으며 미래 교통의 중요한 발전 분야로 간주됩니다. . 하나. 하지만 자율주행을 어렵게 만드는 것은 자동차가 주변에서 일어나는 일을 어떻게 이해할 수 있는지 알아내는 것입니다. 이를 위해서는 자율주행 시스템의 3차원 객체 감지 알고리즘이 주변 환경의 객체의 위치를 포함하여 정확하게 인지하고 묘사할 수 있어야 하며,
 Stable Diffusion 3 논문이 드디어 공개되고, 아키텍처의 세부 사항이 공개되어 Sora를 재현하는 데 도움이 될까요?
Mar 06, 2024 pm 05:34 PM
Stable Diffusion 3 논문이 드디어 공개되고, 아키텍처의 세부 사항이 공개되어 Sora를 재현하는 데 도움이 될까요?
Mar 06, 2024 pm 05:34 PM
StableDiffusion3의 논문이 드디어 나왔습니다! 이 모델은 2주 전에 출시되었으며 Sora와 동일한 DiT(DiffusionTransformer) 아키텍처를 사용합니다. 출시되자마자 큰 화제를 불러일으켰습니다. 이전 버전과 비교하여 StableDiffusion3에서 생성된 이미지의 품질이 크게 향상되었습니다. 이제 다중 테마 프롬프트를 지원하고 텍스트 쓰기 효과도 향상되었으며 더 이상 잘못된 문자가 표시되지 않습니다. StabilityAI는 StableDiffusion3이 800M에서 8B 범위의 매개변수 크기를 가진 일련의 모델임을 지적했습니다. 이 매개변수 범위는 모델이 많은 휴대용 장치에서 직접 실행될 수 있어 AI 사용이 크게 줄어든다는 것을 의미합니다.
 자율주행과 궤도예측에 관한 글은 이 글이면 충분합니다!
Feb 28, 2024 pm 07:20 PM
자율주행과 궤도예측에 관한 글은 이 글이면 충분합니다!
Feb 28, 2024 pm 07:20 PM
자율주행 궤적 예측은 차량의 주행 과정에서 발생하는 다양한 데이터를 분석하여 차량의 향후 주행 궤적을 예측하는 것을 의미합니다. 자율주행의 핵심 모듈인 궤도 예측의 품질은 후속 계획 제어에 매우 중요합니다. 궤적 예측 작업은 풍부한 기술 스택을 보유하고 있으며 자율 주행 동적/정적 인식, 고정밀 지도, 차선, 신경망 아키텍처(CNN&GNN&Transformer) 기술 등에 대한 익숙함이 필요합니다. 시작하기가 매우 어렵습니다! 많은 팬들은 가능한 한 빨리 궤도 예측을 시작하여 함정을 피하기를 희망합니다. 오늘은 궤도 예측을 위한 몇 가지 일반적인 문제와 입문 학습 방법을 살펴보겠습니다. 관련 지식 입문 1. 미리보기 논문이 순서대로 되어 있나요? A: 먼저 설문조사를 보세요, p
 엔드투엔드(End-to-End)와 차세대 자율주행 시스템, 그리고 엔드투엔드 자율주행에 대한 몇 가지 오해에 대해 이야기해볼까요?
Apr 15, 2024 pm 04:13 PM
엔드투엔드(End-to-End)와 차세대 자율주행 시스템, 그리고 엔드투엔드 자율주행에 대한 몇 가지 오해에 대해 이야기해볼까요?
Apr 15, 2024 pm 04:13 PM
지난 달에는 몇 가지 잘 알려진 이유로 업계의 다양한 교사 및 급우들과 매우 집중적인 교류를 가졌습니다. 교환에서 피할 수 없는 주제는 자연스럽게 엔드투엔드와 인기 있는 Tesla FSDV12입니다. 저는 이 기회를 빌어 여러분의 참고와 토론을 위해 지금 이 순간 제 생각과 의견을 정리하고 싶습니다. End-to-End 자율주행 시스템을 어떻게 정의하고, End-to-End 해결을 위해 어떤 문제가 예상되나요? 가장 전통적인 정의에 따르면, 엔드 투 엔드 시스템은 센서로부터 원시 정보를 입력하고 작업과 관련된 변수를 직접 출력하는 시스템을 의미합니다. 예를 들어 이미지 인식에서 CNN은 기존의 특징 추출 + 분류기 방식에 비해 end-to-end 방식으로 호출할 수 있습니다. 자율주행 작업에서는 다양한 센서(카메라/LiDAR)로부터 데이터를 입력받아
 SIMPL: 자율 주행을 위한 간단하고 효율적인 다중 에이전트 동작 예측 벤치마크
Feb 20, 2024 am 11:48 AM
SIMPL: 자율 주행을 위한 간단하고 효율적인 다중 에이전트 동작 예측 벤치마크
Feb 20, 2024 am 11:48 AM
원제목: SIMPL: ASimpleandEfficientMulti-agentMotionPredictionBaselineforAutonomousDriving 논문 링크: https://arxiv.org/pdf/2402.02519.pdf 코드 링크: https://github.com/HKUST-Aerial-Robotics/SIMPL 저자 단위: Hong Kong University of Science 및 기술 DJI 논문 아이디어: 이 논문은 자율주행차를 위한 간단하고 효율적인 모션 예측 기준선(SIMPL)을 제안합니다. 기존 에이전트 센트와 비교
 FisheyeDetNet: 어안 카메라를 기반으로 한 최초의 표적 탐지 알고리즘
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: 어안 카메라를 기반으로 한 최초의 표적 탐지 알고리즘
Apr 26, 2024 am 11:37 AM
표적 탐지는 자율주행 시스템에서 상대적으로 성숙한 문제이며, 그 중 보행자 탐지는 가장 먼저 배포되는 알고리즘 중 하나입니다. 대부분의 논문에서 매우 포괄적인 연구가 수행되었습니다. 그러나 서라운드 뷰를 위한 어안 카메라를 사용한 거리 인식은 상대적으로 덜 연구되었습니다. 큰 방사형 왜곡으로 인해 표준 경계 상자 표현은 어안 카메라에서 구현하기 어렵습니다. 위의 설명을 완화하기 위해 확장된 경계 상자, 타원 및 일반 다각형 디자인을 극/각 표현으로 탐색하고 인스턴스 분할 mIOU 메트릭을 정의하여 이러한 표현을 분석합니다. 제안된 다각형 형태의 모델 fisheyeDetNet은 다른 모델보다 성능이 뛰어나며 동시에 자율 주행을 위한 Valeo fisheye 카메라 데이터 세트에서 49.5% mAP를 달성합니다.




