PyTorch를 사용하여 혼합 전문가 모델(MoE) 구현-일체 포함-php.cn

Mixtral 8x7B의 출시는 개방형 AI 분야, 특히 모두에게 잘 알려진 MoE(Mixture-of-Experts) 개념에서 광범위한 관심을 끌었습니다. MoE(Hybrid Expertise) 개념은 협업 지능을 상징하며 전체가 부분의 합보다 크다는 생각을 구현합니다. MoE 모델은 여러 전문가 모델의 장점을 통합하여 보다 정확한 예측을 제공합니다. 이는 게이트 네트워크와 전문가 네트워크 세트로 구성되며, 각 전문가 네트워크는 특정 작업의 다양한 측면을 처리하는 데 능숙합니다. MoE 모델은 작업과 가중치를 적절하게 할당함으로써 전문가의 전문 지식을 활용하여 전반적인 예측 성능을 향상시킬 수 있습니다. 이 협업 지능형 모델은 AI 분야 개발에 새로운 혁신을 가져왔으며 향후 응용 분야에서 중요한 역할을 할 것입니다.

이 기사에서는 PyTorch를 사용하여 MoE 모델을 구현합니다. 구체적인 코드를 소개하기에 앞서 하이브리드 전문가의 아키텍처에 대해 간략히 소개하겠습니다.

MoE 아키텍처

MoE는 (1) 전문가 네트워크와 (2) 게이트 네트워크의 두 가지 유형의 네트워크로 구성됩니다.

Expert Network는 데이터 하위 집합에서 우수한 성능을 발휘하는 독점 모델을 사용하는 방법입니다. 핵심 개념은 문제에 대한 포괄적인 솔루션을 보장하기 위해 보완적인 강점을 가진 여러 전문가를 통해 문제 공간을 다루는 것입니다. 각 전문가 모델은 고유한 기능과 경험으로 교육되어 전반적인 시스템 성능과 효율성이 향상됩니다. 전문가 네트워크를 활용하면 복잡한 작업과 요구 사항을 효과적으로 처리하고 더 나은 솔루션을 제공할 수 있습니다.

게이트 네트워크는 전문가의 기여를 지시, 조정 또는 관리하는 데 사용되는 네트워크입니다. 다양한 유형의 입력에 대해 다양한 네트워크의 기능을 학습하고 평가하여 특정 입력을 처리하는 데 가장 적합한 네트워크를 결정합니다. 잘 훈련된 게이팅 네트워크는 새로운 입력 벡터를 평가하고 숙련도에 따라 가장 적절한 전문가 또는 전문가 조합에 처리 작업을 할당할 수 있습니다. 게이팅 네트워크는 전문가의 출력과 현재 입력의 관련성에 따라 가중치를 동적으로 조정하여 개인화된 응답을 보장합니다. 가중치를 동적으로 조정하는 이 메커니즘을 통해 게이팅 네트워크가 다양한 상황과 요구 사항에 유연하게 적응할 수 있습니다.

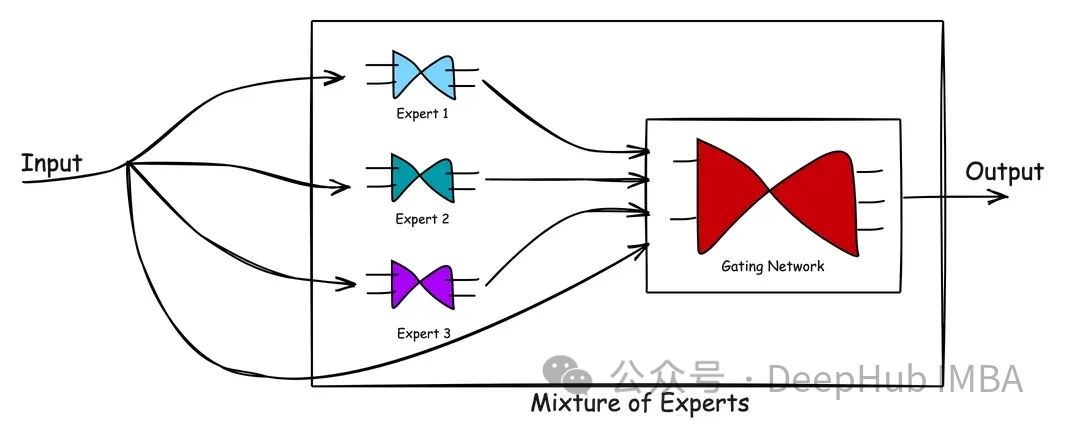
PyTorch를 사용하여 혼합 전문가 모델(MoE) 구현

위 그림은 MoE의 처리 흐름을 보여줍니다. 혼합 전문가 모델의 장점은 단순성입니다. 문제를 해결하는 동안 복잡한 문제 공간과 전문가의 반응을 학습함으로써 MoE 모델은 단일 전문가보다 더 나은 솔루션을 생성하는 데 도움이 됩니다. Gating Network는 시나리오를 평가하고 최고의 전문가에게 작업을 전달하는 효과적인 관리자 역할을 합니다. 새로운 데이터가 입력되면 모델은 새로운 입력에 대한 전문가의 강점을 재평가하여 적응할 수 있으므로 유연한 학습 접근 방식이 가능해집니다. 즉, MoE 모델은 여러 전문가의 지식과 경험을 활용하여 복잡한 문제를 해결합니다. 게이트형 네트워크 관리를 통해 모델은 다양한 시나리오에 따라 작업을 처리하는 데 가장 적합한 전문가를 선택할 수 있습니다. 이 접근 방식의 장점은 단일 전문가보다 더 나은 솔루션을 생성할 수 있는 능력과 새로운 입력 데이터에 적응할 수 있는 유연성입니다. 전반적으로 MoE 모델은 다양하고 복잡한 문제를 해결하는 데 사용할 수 있는 효과적이고 간단한 방법입니다.

MoE는 기계 학습 모델 배포에 큰 이점을 제공합니다. 여기에는 두 가지 주목할만한 이점이 있습니다.

MoE의 핵심 강점은 다양하고 전문적인 전문가 네트워크에 있습니다. MoE의 설정은 단일 모델로는 달성하기 어려운 여러 분야의 문제를 높은 정확도로 처리할 수 있습니다.

MoE는 본질적으로 확장 가능합니다. 작업 복잡성이 증가함에 따라 더 많은 전문가가 시스템에 원활하게 통합되어 다른 전문가 모델을 변경할 필요 없이 전문 지식의 범위를 확장할 수 있습니다. 즉, MoE는 사전 교육을 받은 전문가를 기계 학습 시스템에 패키지하여 시스템이 증가하는 작업 요구 사항에 대처할 수 있도록 도울 수 있습니다.

혼합 전문가 모델은 추천 시스템, 언어 모델링, 다양하고 복잡한 예측 작업을 비롯한 다양한 분야에 적용됩니다. GPT-4가 다수의 전문가로 구성되어 있다는 소문이 돌고 있다. 확인할 수는 없지만 gpt-4와 같은 모델은 MoE 접근 방식을 통해 여러 모델의 기능을 활용하여 최상의 결과를 제공합니다.

Pytorch code

여기에서는 Mixtral 8x7B와 같은 대형 모델에 사용되는 MOE 기술을 논의하지 않고 대신 모든 작업에 적용할 수 있는 간단한 사용자 정의 MOE를 작성합니다. code MOE의 작동 원리는 MOE가 대형 모델에서 어떻게 작동하는지 이해하는 데 매우 도움이 됩니다.

아래에서는 PyTorch의 코드 구현을 하나씩 소개하겠습니다.

라이브러리 가져오기:

import torch import torch.nn as nn import torch.optim as optim

로그인 후 복사

전문가 모델 정의:

class Expert(nn.Module): def __init__(self, input_dim, hidden_dim, output_dim): super(Expert, self).__init__() self.layer1 = nn.Linear(input_dim, hidden_dim) self.layer2 = nn.Linear(hidden_dim, output_dim)  def forward(self, x): x = torch.relu(self.layer1(x)) return torch.softmax(self.layer2(x), dim=1)

로그인 후 복사

여기서 간단한 전문가 모델을 정의합니다. Relu 활성화를 사용하고 마지막으로 소프트맥스 출력을 사용하는 2계층 MLP임을 알 수 있습니다. 분류 확률.

게이트 모델 정의:

# Define the gating model class Gating(nn.Module): def __init__(self, input_dim,num_experts, dropout_rate=0.1): super(Gating, self).__init__()  # Layers self.layer1 = nn.Linear(input_dim, 128) self.dropout1 = nn.Dropout(dropout_rate)  self.layer2 = nn.Linear(128, 256) self.leaky_relu1 = nn.LeakyReLU() self.dropout2 = nn.Dropout(dropout_rate)  self.layer3 = nn.Linear(256, 128) self.leaky_relu2 = nn.LeakyReLU() self.dropout3 = nn.Dropout(dropout_rate)  self.layer4 = nn.Linear(128, num_experts)  def forward(self, x): x = torch.relu(self.layer1(x)) x = self.dropout1(x)  x = self.layer2(x) x = self.leaky_relu1(x) x = self.dropout2(x)  x = self.layer3(x) x = self.leaky_relu2(x) x = self.dropout3(x)  return torch.softmax(self.layer4(x), dim=1)

로그인 후 복사

门控模型更复杂，有三个线性层和dropout层用于正则化以防止过拟合。它使用ReLU和LeakyReLU激活函数引入非线性。最后一层的输出大小等于专家的数量，并对这些输出应用softmax函数。输出权重，这样可以将专家的输出与之结合。

说明：其实门控网络，或者叫路由网络是MOE中最复杂的部分，因为它涉及到控制输入到那个专家模型，所以门控网络也有很多个设计方案，例如（如果我没记错的话）Mixtral 8x7B 只是取了8个专家中的top2。所以我们这里不详细讨论各种方案，只是介绍其基本原理和代码实现。

完整的MOE模型：

class MoE(nn.Module): def __init__(self, trained_experts): super(MoE, self).__init__() self.experts = nn.ModuleList(trained_experts) num_experts = len(trained_experts) # Assuming all experts have the same input dimension input_dim = trained_experts[0].layer1.in_features self.gating = Gating(input_dim, num_experts)  def forward(self, x): # Get the weights from the gating network weights = self.gating(x)  # Calculate the expert outputs outputs = torch.stack([expert(x) for expert in self.experts], dim=2)  # Adjust the weights tensor shape to match the expert outputs weights = weights.unsqueeze(1).expand_as(outputs)  # Multiply the expert outputs with the weights and # sum along the third dimension return torch.sum(outputs * weights, dim=2)

로그인 후 복사

这里主要看前向传播的代码，通过输入计算出权重和每个专家给出输出的预测，最后使用权重将所有专家的结果求和最终得到模型的输出。

这个是不是有点像“集成学习”。

测试

下面我们来对我们的实现做个简单的测试，首先生成一个简单的数据集:

# Generate the dataset num_samples = 5000 input_dim = 4 hidden_dim = 32  # Generate equal numbers of labels 0, 1, and 2 y_data = torch.cat([ torch.zeros(num_samples // 3), torch.ones(num_samples // 3), torch.full((num_samples - 2 * (num_samples // 3),), 2)# Filling the remaining to ensure exact num_samples ]).long()  # Biasing the data based on the labels x_data = torch.randn(num_samples, input_dim)  for i in range(num_samples): if y_data[i] == 0: x_data[i, 0] += 1# Making x[0] more positive elif y_data[i] == 1: x_data[i, 1] -= 1# Making x[1] more negative elif y_data[i] == 2: x_data[i, 0] -= 1# Making x[0] more negative  # Shuffle the data to randomize the order indices = torch.randperm(num_samples) x_data = x_data[indices] y_data = y_data[indices]  # Verify the label distribution y_data.bincount()  # Shuffle the data to ensure x_data and y_data remain aligned shuffled_indices = torch.randperm(num_samples) x_data = x_data[shuffled_indices] y_data = y_data[shuffled_indices]  # Splitting data for training individual experts # Use the first half samples for training individual experts x_train_experts = x_data[:int(num_samples/2)] y_train_experts = y_data[:int(num_samples/2)]  mask_expert1 = (y_train_experts == 0) | (y_train_experts == 1) mask_expert2 = (y_train_experts == 1) | (y_train_experts == 2) mask_expert3 = (y_train_experts == 0) | (y_train_experts == 2)  # Select an almost equal number of samples for each expert num_samples_per_expert = \ min(mask_expert1.sum(), mask_expert2.sum(), mask_expert3.sum())  x_expert1 = x_train_experts[mask_expert1][:num_samples_per_expert] y_expert1 = y_train_experts[mask_expert1][:num_samples_per_expert]  x_expert2 = x_train_experts[mask_expert2][:num_samples_per_expert] y_expert2 = y_train_experts[mask_expert2][:num_samples_per_expert]  x_expert3 = x_train_experts[mask_expert3][:num_samples_per_expert] y_expert3 = y_train_experts[mask_expert3][:num_samples_per_expert]  # Splitting the next half samples for training MoE model and for testing x_remaining = x_data[int(num_samples/2)+1:] y_remaining = y_data[int(num_samples/2)+1:]  split = int(0.8 * len(x_remaining)) x_train_moe = x_remaining[:split] y_train_moe = y_remaining[:split]  x_test = x_remaining[split:] y_test = y_remaining[split:]  print(x_train_moe.shape,"\n", x_test.shape,"\n", x_expert1.shape,"\n", x_expert2.shape,"\n", x_expert3.shape)

로그인 후 복사

这段代码创建了一个合成数据集，其中包含三个类标签——0、1和2。基于类标签对特征进行操作，从而在数据中引入一些模型可以学习的结构。

数据被分成针对个别专家的训练集、MoE模型和测试集。我们确保专家模型是在一个子集上训练的，这样第一个专家在标签0和1上得到很好的训练，第二个专家在标签1和2上得到更好的训练，第三个专家看到更多的标签2和0。

我们期望的结果是：虽然每个专家对标签0、1和2的分类准确率都不令人满意，但通过结合三位专家的决策，MoE将表现出色。

模型初始化和训练设置:

# Define hidden dimension output_dim = 3 hidden_dim = 32  epochs = 500 learning_rate = 0.001   # Instantiate the experts expert1 = Expert(input_dim, hidden_dim, output_dim) expert2 = Expert(input_dim, hidden_dim, output_dim) expert3 = Expert(input_dim, hidden_dim, output_dim)  # Set up loss criterion = nn.CrossEntropyLoss()  # Optimizers for experts optimizer_expert1 = optim.Adam(expert1.parameters(), lr=learning_rate) optimizer_expert2 = optim.Adam(expert2.parameters(), lr=learning_rate) optimizer_expert3 = optim.Adam(expert3.parameters(), lr=learning_rate)

로그인 후 복사

实例化了专家模型和MoE模型。定义损失函数来计算训练损失，并为每个模型设置优化器，在训练过程中执行权重更新。

训练的步骤也非常简单

# Training loop for expert 1 for epoch in range(epochs):optimizer_expert1.zero_grad()outputs_expert1 = expert1(x_expert1)loss_expert1 = criterion(outputs_expert1, y_expert1)loss_expert1.backward()optimizer_expert1.step()  # Training loop for expert 2 for epoch in range(epochs):optimizer_expert2.zero_grad()outputs_expert2 = expert2(x_expert2)loss_expert2 = criterion(outputs_expert2, y_expert2)loss_expert2.backward()optimizer_expert2.step()  # Training loop for expert 3 for epoch in range(epochs):optimizer_expert3.zero_grad()outputs_expert3 = expert3(x_expert3)loss_expert3 = criterion(outputs_expert3, y_expert3)loss_expert3.backward()

로그인 후 복사

每个专家使用基本的训练循环在不同的数据子集上进行单独的训练。循环迭代指定数量的epoch。

下面是我们MOE的训练

# Create the MoE model with the trained experts moe_model = MoE([expert1, expert2, expert3])  # Train the MoE model optimizer_moe = optim.Adam(moe_model.parameters(), lr=learning_rate) for epoch in range(epochs):optimizer_moe.zero_grad()outputs_moe = moe_model(x_train_moe)loss_moe = criterion(outputs_moe, y_train_moe)loss_moe.backward()optimizer_moe.step()

로그인 후 복사

MoE模型是由先前训练过的专家创建的，然后在单独的数据集上进行训练。训练过程类似于单个专家的训练，但现在门控网络的权值在训练过程中更新。

最后我们的评估函数：

# Evaluate all models def evaluate(model, x, y):with torch.no_grad():outputs = model(x)_, predicted = torch.max(outputs, 1)correct = (predicted == y).sum().item()accuracy = correct / len(y)return accuracy

로그인 후 복사

evaluate函数计算模型在给定数据上的精度(x代表样本，y代表预期标签)。准确度计算为正确预测数与预测总数之比。

结果如下：

accuracy_expert1 = evaluate(expert1, x_test, y_test) accuracy_expert2 = evaluate(expert2, x_test, y_test) accuracy_expert3 = evaluate(expert3, x_test, y_test) accuracy_moe = evaluate(moe_model, x_test, y_test)  print("Expert 1 Accuracy:", accuracy_expert1) print("Expert 2 Accuracy:", accuracy_expert2) print("Expert 3 Accuracy:", accuracy_expert3) print("Mixture of Experts Accuracy:", accuracy_moe)  #Expert 1 Accuracy: 0.466 #Expert 2 Accuracy: 0.496 #Expert 3 Accuracy: 0.378 #Mixture of Experts Accuracy: 0.614

로그인 후 복사

可以看到

专家1正确预测了测试数据集中大约46.6%的样本的类标签。

专家2表现稍好，正确预测率约为49.6%。

专家3在三位专家中准确率最低，正确预测的样本约为37.8%。

而MoE模型显著优于每个专家，总体准确率约为61.4%。