Ford-Fulkerson 알고리즘을 구문 분석하고 Python을 통해 구현합니다.
Ford-Fulkerson 알고리즘은 네트워크의 최대 트래픽을 계산하는 데 사용되는 그리디 알고리즘입니다. 원칙은 남은 용량이 양수인 증가 경로를 찾는 것입니다. 증가 경로가 발견되는 한 계속해서 경로를 추가하고 트래픽을 계산할 수 있습니다. 증가 경로가 더 이상 존재하지 않을 때까지 최대 유량을 얻을 수 있습니다.
Ford-Fulkerson 알고리즘 용어
남은 용량: 용량에서 흐름을 뺀 값입니다. Ford-Fulkerson 알고리즘에서 남은 용량은 계속 경로가 될 수 있기 전의 양수입니다.
잔여 네트워크: 잔여 용량을 용량으로 사용하는 정점과 가장자리가 동일한 네트워크입니다.
증강 경로: 잔여 그래프의 소스 지점에서 수신 지점까지의 경로이며 최종 용량은 0입니다.
Ford-Fulkerson 알고리즘 원리 예
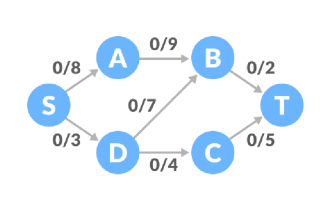
예를 들어 보면 흐름 네트워크의 모든 가장자리의 초기 트래픽이 0이고 해당하는 최대 용량 제한이 있습니다. S이고 수신 지점은 T입니다.
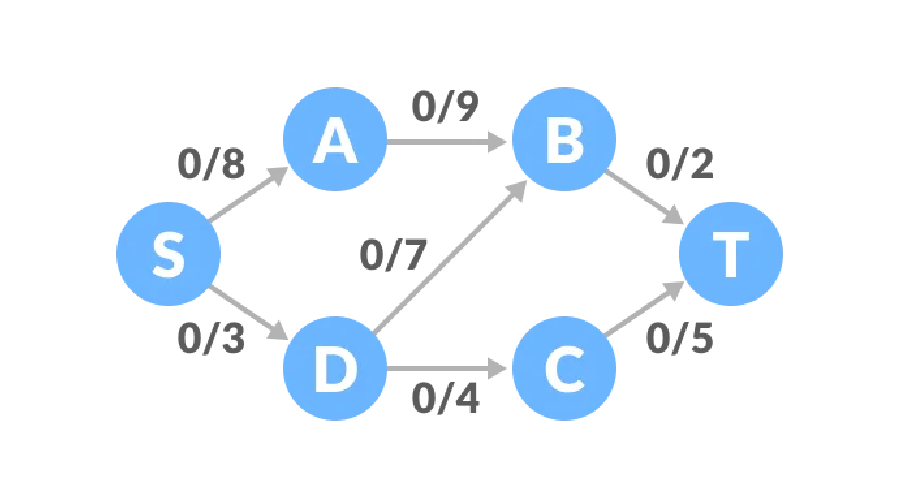
경로 1, S-A-B-T 경로의 남은 용량은 8, 9, 2이고 최소값은 2이므로 경로 1의 트래픽은 2, 네트워크 다이어그램의 트래픽은 2입니다.
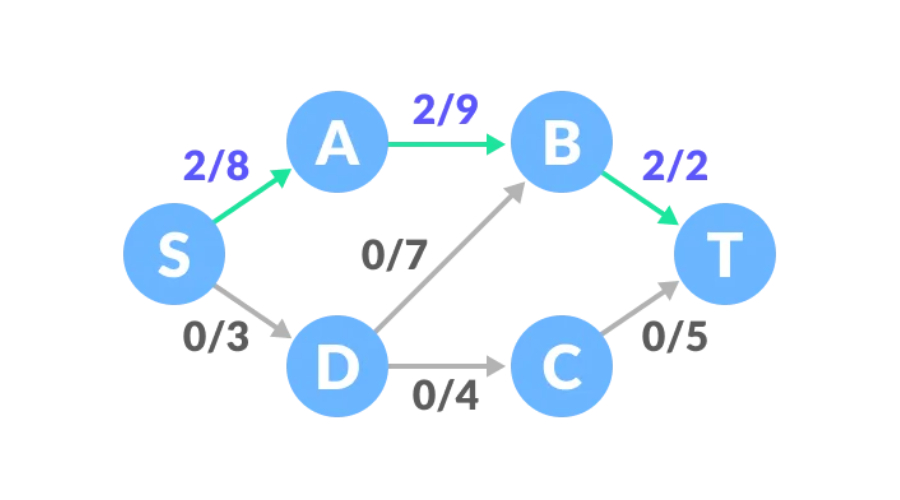
경로 2, S-D-C-T 경로의 남은 용량은 3, 4, 5이고 최소값은 3이므로 트래픽을 3씩 늘릴 수 있고 네트워크 트래픽은 5입니다.
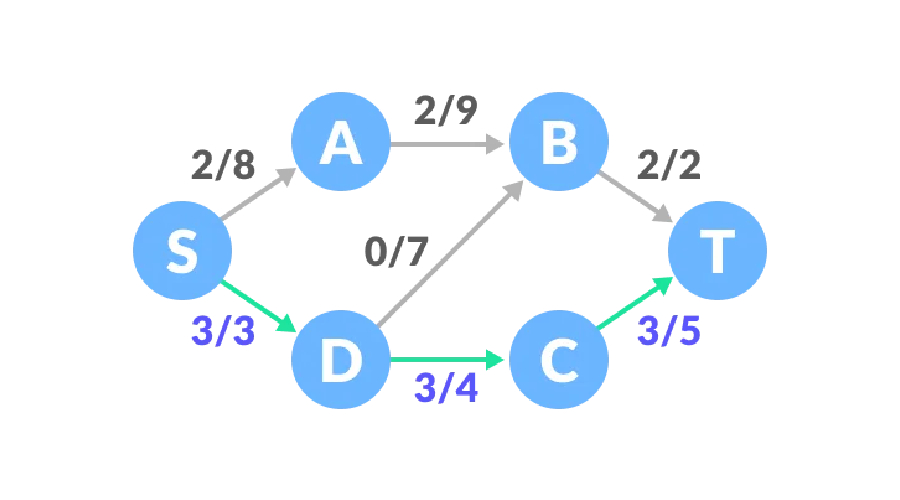
Path 3, S-A-B-D-C-T 경로의 남은 용량은 6, 7, 7, 1, 2이고 최소값은 1이므로 트래픽이 1씩 증가하고 네트워크 트래픽은 6이 됩니다.
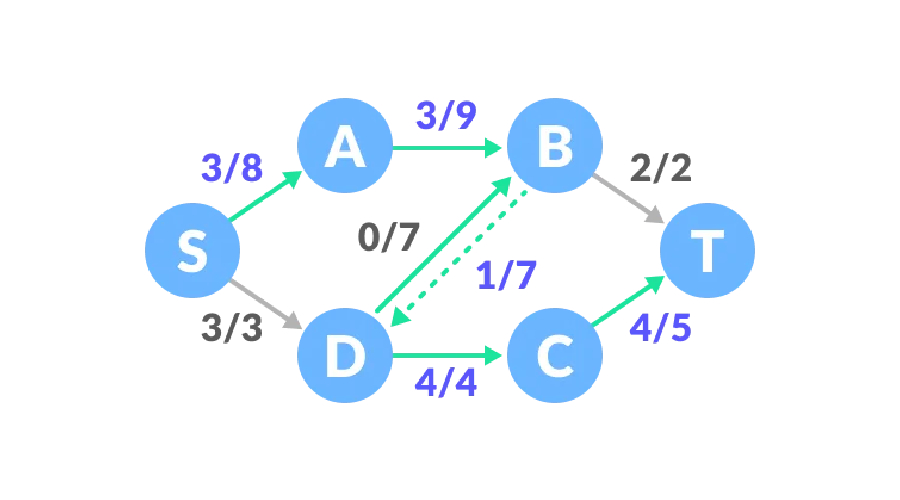
이 시점에서 긍정적인 잔여 용량은 없으며 이 흐름 네트워크의 최대 흐름은 6입니다.
Python은 Ford-Fulkerson 알고리즘을 구현합니다
from collections import defaultdict
class Graph:
def __init__(self, graph):
self.graph = graph
self. ROW = len(graph)
def searching_algo_BFS(self, s, t, parent):
visited = [False] * (self.ROW)
queue = []
queue.append(s)
visited[s] = True
while queue:
u = queue.pop(0)
for ind, val in enumerate(self.graph[u]):
if visited[ind] == False and val > 0:
queue.append(ind)
visited[ind] = True
parent[ind] = u
return True if visited[t] else False
def ford_fulkerson(self, source, sink):
parent = [-1] * (self.ROW)
max_flow = 0
while self.searching_algo_BFS(source, sink, parent):
path_flow = float("Inf")
s = sink
while(s != source):
path_flow = min(path_flow, self.graph[parent[s]][s])
s = parent[s]
max_flow += path_flow
v = sink
while(v != source):
u = parent[v]
self.graph[u][v] -= path_flow
self.graph[v][u] += path_flow
v = parent[v]
return max_flow
graph = [[0, 8, 0, 0, 3, 0],
[0, 0, 9, 0, 0, 0],
[0, 0, 0, 0, 7, 2],
[0, 0, 0, 0, 0, 5],
[0, 0, 7, 4, 0, 0],
[0, 0, 0, 0, 0, 0]]
g = Graph(graph)
source = 0
sink = 5
print("Max Flow: %d " % g.ford_fulkerson(source, sink))위 내용은 Ford-Fulkerson 알고리즘을 구문 분석하고 Python을 통해 구현합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7515
7515
 15
15
 1378
1378
 52
52
 79
79
 11
11
 53
53
 19
19
 19
19
 64
64
 C#에서 그리디 알고리즘을 구현하는 방법
Sep 19, 2023 am 11:48 AM
C#에서 그리디 알고리즘을 구현하는 방법
Sep 19, 2023 am 11:48 AM
C#에서 그리디 알고리즘을 구현하는 방법 그리디 알고리즘(Greedy Algorithm)은 일반적으로 사용되는 문제 해결 방법으로 전역 최적 솔루션을 얻기 위해 매번 현재 최적 솔루션을 선택합니다. C#에서는 그리디 알고리즘을 사용하여 많은 실제 문제를 해결할 수 있습니다. 이 문서에서는 C#에서 그리디 알고리즘을 구현하는 방법을 소개하고 구체적인 코드 예제를 제공합니다. 1. 그리디 알고리즘의 기본 원리 그리디 알고리즘의 기본 아이디어는 후속 단계의 가능한 영향에 관계없이 매번 현재 최적의 솔루션을 선택하는 것입니다. 이런 생각이
 그리디 알고리즘을 사용하여 PHP에서 최소 코인 변경 문제에 대한 효율적인 솔루션을 구현하는 방법은 무엇입니까?
Sep 19, 2023 am 10:22 AM
그리디 알고리즘을 사용하여 PHP에서 최소 코인 변경 문제에 대한 효율적인 솔루션을 구현하는 방법은 무엇입니까?
Sep 19, 2023 am 10:22 AM
그리디 알고리즘을 사용하여 PHP에서 최소 코인 변경 문제에 대한 효율적인 솔루션을 구현하는 방법은 무엇입니까? 서론: 일상 생활에서 우리는 종종 변화가 필요합니다. 특히 쇼핑이나 거래를 할 때 더욱 그렇습니다. 최대한 적은 코인을 사용하기 위해서는 가능한 한 적은 코인을 사용하여 거스름돈 금액을 합산해야 합니다. 컴퓨터 프로그래밍에서는 그리디 알고리즘을 사용하여 이 문제를 해결하여 효율적인 솔루션을 얻을 수 있습니다. 이 기사에서는 최소 코인 변경 문제에 대한 효율적인 솔루션을 얻기 위해 PHP에서 그리디 알고리즘을 사용하는 방법을 소개하고 해당 코드 예제를 제공합니다.
 Ford-Fulkerson 알고리즘을 구문 분석하고 Python을 통해 구현합니다.
Jan 22, 2024 pm 08:09 PM
Ford-Fulkerson 알고리즘을 구문 분석하고 Python을 통해 구현합니다.
Jan 22, 2024 pm 08:09 PM
Ford-Fulkerson 알고리즘은 네트워크의 최대 유량을 계산하는 데 사용되는 그리디 알고리즘입니다. 원칙은 남은 용량이 양수인 증가 경로를 찾는 것입니다. 증가 경로가 발견되는 한 계속해서 경로를 추가하고 트래픽을 계산할 수 있습니다. 증가 경로가 더 이상 존재하지 않을 때까지 최대 유량을 얻을 수 있습니다. Ford-Fulkerson 알고리즘의 잔여 용량이라는 용어는 용량에서 흐름을 빼는 것입니다. Ford-Fulkerson 알고리즘에서 잔여 용량은 경로로 계속 사용되기 전에 양수입니다. 잔여 네트워크(Residual network): 잔여 용량을 용량으로 사용하는 정점과 가장자리가 동일한 네트워크입니다. 증강 경로(Augmented path): 잔차 그래프의 소스 지점에서 수신 지점까지의 경로이며 최종 용량은 0입니다. Ford-Fulkerson 알고리즘 원리 예제의 가능한 개요
 Python을 사용하여 그리디 알고리즘을 구현하는 방법은 무엇입니까?
Sep 19, 2023 am 11:43 AM
Python을 사용하여 그리디 알고리즘을 구현하는 방법은 무엇입니까?
Sep 19, 2023 am 11:43 AM
Python을 사용하여 그리디 알고리즘을 구현하는 방법은 무엇입니까? Greedy Algorithm은 최적의 하부 구조 속성 문제를 해결하는 데 적합한 간단하고 효과적인 알고리즘입니다. 글로벌 최적의 솔루션을 찾기 위해 선택의 각 단계에서 현재 상태에서 최선의 선택을 취합니다. 이 기사에서는 Python을 사용하여 그리디 알고리즘을 구현하는 방법을 구체적인 코드 예제와 함께 소개합니다. 1. 그리디 알고리즘의 기본 아이디어 그리디 알고리즘의 기본 아이디어는 각 단계에서 현재 상태에서 최적의 해를 선택한 후,
 PHP를 사용하여 그리디 알고리즘을 작성하는 방법
Jul 07, 2023 pm 03:45 PM
PHP를 사용하여 그리디 알고리즘을 작성하는 방법
Jul 07, 2023 pm 03:45 PM
Greedy 알고리즘을 작성하기 위해 PHP를 사용하는 방법 Greedy 알고리즘(Greedy 알고리즘)은 일종의 최적화 문제를 해결하는 데 사용되는 간단하고 효과적인 알고리즘입니다. 기본 아이디어는 미래의 결과에 관계없이 각 단계에서 현재 가장 좋아 보이는 선택을 하는 것입니다. 이 기사에서는 PHP를 사용하여 그리디 알고리즘을 작성하는 방법을 소개하고 관련 코드 예제를 제공합니다. 1. 문제 설명 그리디 알고리즘을 설명하기 전에 먼저 이해를 돕기 위해 구체적인 문제를 정의해 보겠습니다. 일련의 작업이 있고 각 작업에는 시작이 있다고 가정합니다.
 그리디 알고리즘과 C++에서의 구현
Aug 22, 2023 am 10:04 AM
그리디 알고리즘과 C++에서의 구현
Aug 22, 2023 am 10:04 AM
그리디 알고리즘은 일반적으로 사용되는 알고리즘 아이디어로 많은 문제에서 널리 사용됩니다. 핵심 아이디어는 장기적인 영향을 고려하지 않고 각 단계에서 결정을 내릴 때 즉각적인 최적의 솔루션만 고려하는 것입니다. C++에서 그리디 알고리즘의 구현에는 정렬 및 데이터 처리와 같은 기본 작업이 포함되는 경우가 많습니다. 아래에서는 몇 가지 일반적인 문제에 대한 그리디 알고리즘의 아이디어와 C++에서의 구현을 소개합니다. 1. 활동 일정 문제 주어진 활동에는 각 활동마다 시작 시간과 종료 시간이 있으며, 한 사람은 한 번에 하나의 활동에만 참여할 수 있습니다.
 Java를 사용하여 그리디 알고리즘을 구현하는 방법
Sep 19, 2023 am 11:13 AM
Java를 사용하여 그리디 알고리즘을 구현하는 방법
Sep 19, 2023 am 11:13 AM
Greedy 알고리즘을 구현하기 위해 Java를 사용하는 방법 Greedy 알고리즘(GreedyAlgorithm)은 문제 해결을 위한 알고리즘 아이디어로, 각 단계에서 현재 최적 솔루션을 선택하고, 결국에는 각 로컬 최적 솔루션을 통해 전역 최적 솔루션에 도달하기를 희망하는 것이 특징입니다. 그리디 알고리즘의 간단하고 효율적인 특성으로 인해 일부 최적화 문제나 특정 특정 문제를 해결할 때 일반적으로 사용되는 알고리즘이 됩니다. 이 기사에서는 Java를 사용하여 그리디 알고리즘을 구현하는 방법을 소개하고 구체적인 코드 예제를 제공합니다. 1. 그리디 알고리즘의 기본 개념 그리디 알고리즘의 기초
 최소 코인 수를 찾는 탐욕 알고리즘용 C/C++ 프로그램
Sep 19, 2023 pm 11:01 PM
최소 코인 수를 찾는 탐욕 알고리즘용 C/C++ 프로그램
Sep 19, 2023 pm 11:01 PM
그리디 알고리즘(Greedy Algorithm)은 주어진 문제에 대한 최적의 해를 찾는 데 사용되는 알고리즘이다. 그리디 알고리즘은 각 부분에 대한 로컬 최적 솔루션(문제의 한 부분에 대한 최적 솔루션)을 찾는 방식으로 작동하므로 전역 최적 솔루션을 찾을 수 있음을 보여줍니다. 이 문제에서는 Greedy Algorithm 알고리즘을 사용하여 주어진 합계를 구성할 수 있는 최소 동전/노트 수를 찾습니다. 이를 위해 우리는 유효한 모든 동전이나 지폐, 즉 {1,2,5,10,20,50,100,200,500,2000} 단위를 고려할 것입니다. 합계를 구성하는 데 필요한 동전/노트의 수를 반환해야 합니다. 문맥을 더 잘 이해하기 위해 몇 가지 예를 들어 보겠습니다. - 예 1 - 입력: 1231 출력: 7 설명 - 500루피 지폐 2개가 필요합니다.




