인공 신경망에 시그모이드 함수 적용

인공 신경망에서 시그모이드 함수는 비선형 특성을 도입하기 위해 뉴런의 활성화 함수로 자주 사용됩니다. 이를 통해 신경망은 더욱 복잡한 결정 경계를 학습하고 이미지 인식, 자연어 처리, 음성 인식 등 다양한 애플리케이션에서 중요한 역할을 할 수 있습니다.
시그모이드 함수는 입력 값을 0과 1 사이의 값으로 매핑할 수 있는 일반적으로 사용되는 수학 함수이므로 이진 분류 및 로지스틱 회귀 문제에 널리 사용되었습니다. 이 함수는 처음에는 천천히 증가하다가 빠르게 1에 접근하고 결국에는 수평을 이루는 "S" 모양이 특징입니다.
시그모이드 함수 이해하기
시그모이드 함수는 입력 값을 0과 1 사이의 범위에 매핑하는 데 사용되는 일반적으로 사용되는 수학 함수입니다. 수학적 정의는 1/(1+e^(-x))입니다. 여기서 x는 입력 값이고 e는 상수 2.718입니다. 이 함수는 이진 분류 및 로지스틱 회귀 문제에 매우 유용합니다. 값 범위는 (0,1)이고 도메인은 (-무한대, +무한대)입니다. S자형 함수의 특징은 실제 입력을 확률 값으로 변환할 수 있다는 점이므로 기계 학습 및 통계 분야에서 모델의 출력 레이어에 자주 사용됩니다.
시그모이드 함수의 주요 속성 중 하나는 입력 값이 증가함에 따라 출력 값이 "S" 모양의 곡선을 나타낸다는 것입니다. 입력 값이 증가함에 따라 출력 값은 점차 증가하여 결국 1에 가까워집니다. 이 기능은 이진 분류 문제에서 결정 경계를 모델링하는 데 중요한 기능을 제공합니다.
시그모이드 함수의 또 다른 중요한 속성은 신경망 훈련에서 중요한 역할을 하는 도함수입니다. 시그모이드 함수의 도함수는 f(x)(1-f(x))로 정의됩니다. 여기서 f(x)는 함수의 출력을 나타냅니다. 파생 상품이 존재하면 신경망이 뉴런의 가중치와 편향을 보다 효과적으로 조정할 수 있어 네트워크의 성능이 향상됩니다. 도함수를 계산함으로써 네트워크는 손실 함수의 기울기를 기반으로 매개변수를 업데이트할 수 있으므로 네트워크가 점진적으로 최적화되고 정확도가 향상될 수 있습니다. 도함수를 사용하여 네트워크를 훈련시키는 이 방법은 딥러닝 분야에서 널리 사용되며, 이를 통해 신경망은 다양한 복잡한 작업을 학습하고 이에 적응할 수 있습니다.
시그모이드 함수 외에도 ReLU, tanh 등 시그모이드 함수의 한계를 보완할 수 있는 활성화 함수가 있습니다. 시그모이드 함수의 출력은 항상 0과 1 사이이므로 네트워크의 출력이 1보다 크거나 0보다 작아야 할 때 문제가 발생할 수 있습니다. ReLU 함수는 양수를 변경하지 않고 음수를 0으로 매핑하여 이 문제를 해결할 수 있습니다. 또한 tanh 함수는 일반적으로 사용되는 활성화 함수이기도 하며 출력 범위는 -1에서 1 사이로 시그모이드 함수보다 유연합니다. 따라서 신경망을 설계할 때 특정 요구 사항에 따라 다양한 활성화 함수를 선택하여 더 나은 결과를 얻을 수 있습니다.
그래프를 사용하여 시그모이드 함수를 시각화하면 그 속성을 더 잘 이해하는 데 도움이 됩니다. 그래프는 함수가 취한 "S" 모양과 입력 값이 변경됨에 따라 출력 값이 어떻게 변경되는지 보여줍니다.
인공 신경망의 시그모이드 함수
시그모이드 함수는 일반적으로 인공 신경망의 활성화 함수로 사용됩니다. 피드포워드 신경망에서 각 뉴런의 출력은 모델에 비선형 특성을 도입할 수 있는 시그모이드 함수에 의해 처리됩니다. 비선형 특성의 도입은 신경망이 더 복잡한 결정 경계를 학습할 수 있게 하여 특정 작업에 대한 성능을 향상시키기 때문에 중요합니다.
장점:
- 0과 1 사이의 출력 값을 생성하여 이진 분류 및 로지스틱 회귀 문제에 도움이 됩니다.
- 미분 가능이란 도함수를 계산할 수 있으며 뉴런의 가중치와 편향을 조정하여 네트워크를 쉽게 최적화할 수 있다는 의미입니다.
단점:
- 0 또는 1에 가까운 출력 값을 생성할 수 있어 최적화 알고리즘에 문제가 발생할 수 있습니다.
- 시그모이드 함수의 기울기는 출력 값 0 또는 1 근처에서 매우 작아지기 때문에 최적화 알고리즘이 뉴런의 가중치와 편향을 조정하기가 어렵습니다.
위 내용은 인공 신경망에 시그모이드 함수 적용의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7518
7518
 15
15
 1378
1378
 52
52
 81
81
 11
11
 53
53
 19
19
 21
21
 68
68
 RNN, LSTM 및 GRU의 개념, 차이점, 장점 및 단점을 살펴보세요.
Jan 22, 2024 pm 07:51 PM
RNN, LSTM 및 GRU의 개념, 차이점, 장점 및 단점을 살펴보세요.
Jan 22, 2024 pm 07:51 PM
시계열 데이터에서는 관측값 간에 종속성이 있으므로 서로 독립적이지 않습니다. 그러나 기존 신경망은 각 관측값을 독립적인 것으로 취급하므로 시계열 데이터를 모델링하는 모델의 기능이 제한됩니다. 이 문제를 해결하기 위해 네트워크의 데이터 포인트 간의 종속성을 설정하여 시계열 데이터의 동적 특성을 캡처하는 메모리 개념을 도입한 RNN(Recurrent Neural Network)이 도입되었습니다. RNN은 반복 연결을 통해 이전 정보를 현재 관찰에 전달하여 미래 값을 더 잘 예측할 수 있습니다. 이는 RNN을 시계열 데이터와 관련된 작업을 위한 강력한 도구로 만듭니다. 그러나 RNN은 어떻게 이런 종류의 메모리를 달성합니까? RNN은 신경망의 피드백 루프를 통해 메모리를 구현합니다. 이것이 RNN과 기존 신경망의 차이점입니다.
 신경망의 FLOPS(부동 소수점 피연산자) 계산
Jan 22, 2024 pm 07:21 PM
신경망의 FLOPS(부동 소수점 피연산자) 계산
Jan 22, 2024 pm 07:21 PM
FLOPS는 컴퓨터 성능 평가 표준 중 하나로 초당 부동 소수점 연산 횟수를 측정하는 데 사용됩니다. 신경망에서 FLOPS는 모델의 계산 복잡성과 컴퓨팅 리소스 활용도를 평가하는 데 자주 사용됩니다. 컴퓨터의 컴퓨팅 성능과 효율성을 측정하는 데 사용되는 중요한 지표입니다. 신경망은 데이터 분류, 회귀, 클러스터링과 같은 작업을 수행하는 데 사용되는 여러 계층의 뉴런으로 구성된 복잡한 모델입니다. 신경망의 훈련 및 추론에는 수많은 행렬 곱셈, 컨볼루션 및 기타 계산 작업이 필요하므로 계산 복잡성이 매우 높습니다. FLOPS(FloatingPointOperationsperSecond)는 신경망의 계산 복잡성을 측정하여 모델의 계산 리소스 사용 효율성을 평가하는 데 사용할 수 있습니다. 실패
 텍스트 분류를 위한 양방향 LSTM 모델 사용 사례 연구
Jan 24, 2024 am 10:36 AM
텍스트 분류를 위한 양방향 LSTM 모델 사용 사례 연구
Jan 24, 2024 am 10:36 AM
양방향 LSTM 모델은 텍스트 분류에 사용되는 신경망입니다. 다음은 텍스트 분류 작업에 양방향 LSTM을 사용하는 방법을 보여주는 간단한 예입니다. 먼저 필요한 라이브러리와 모듈을 가져와야 합니다. importosimportnumpyasnpfromkeras.preprocessing.textimportTokenizerfromkeras.preprocessing.sequenceimportpad_sequencesfromkeras.modelsimportSequentialfromkeras.layersimportDense,Em
 퍼지 신경망의 정의 및 구조 분석
Jan 22, 2024 pm 09:09 PM
퍼지 신경망의 정의 및 구조 분석
Jan 22, 2024 pm 09:09 PM
퍼지 신경망은 퍼지 논리와 신경망을 결합하여 기존 신경망으로 처리하기 어려운 퍼지 또는 불확실한 문제를 해결하는 하이브리드 모델입니다. 그 디자인은 인간 인지의 모호함과 불확실성에서 영감을 얻어 제어 시스템, 패턴 인식, 데이터 마이닝 및 기타 분야에서 널리 사용됩니다. 퍼지 신경망의 기본 아키텍처는 퍼지 하위 시스템과 신경 하위 시스템으로 구성됩니다. 퍼지 하위 시스템은 퍼지 논리를 사용하여 입력 데이터를 처리하고 이를 퍼지 세트로 변환하여 입력 데이터의 퍼지 및 불확실성을 표현합니다. 신경 하위 시스템은 신경망을 사용하여 분류, 회귀 또는 클러스터링과 같은 작업을 위한 퍼지 세트를 처리합니다. 퍼지 하위 시스템과 신경 하위 시스템 간의 상호 작용으로 인해 퍼지 신경망은 더욱 강력한 처리 능력을 갖게 되며 다음과 같은 작업을 수행할 수 있습니다.
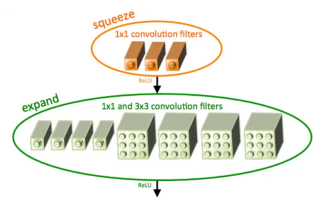 SqueezeNet 소개 및 특징
Jan 22, 2024 pm 07:15 PM
SqueezeNet 소개 및 특징
Jan 22, 2024 pm 07:15 PM
SqueezeNet은 높은 정확도와 낮은 복잡성 사이의 적절한 균형을 유지하는 작고 정밀한 알고리즘으로, 리소스가 제한된 모바일 및 임베디드 시스템에 이상적입니다. 2016년 DeepScale, University of California, Berkeley 및 Stanford University의 연구원들은 작고 효율적인 CNN(컨볼루션 신경망)인 SqueezeNet을 제안했습니다. 최근 몇 년 동안 연구원들은 SqueezeNetv1.1 및 SqueezeNetv2.0을 포함하여 SqueezeNet에 대한 몇 가지 개선 사항을 적용했습니다. 두 버전 모두의 개선으로 정확도가 향상될 뿐만 아니라 계산 비용도 절감됩니다. ImageNet 데이터 세트에서 SqueezeNetv1.1의 정확도
 컨벌루션 신경망을 사용한 이미지 노이즈 제거
Jan 23, 2024 pm 11:48 PM
컨벌루션 신경망을 사용한 이미지 노이즈 제거
Jan 23, 2024 pm 11:48 PM
컨벌루션 신경망은 이미지 노이즈 제거 작업에서 좋은 성능을 발휘합니다. 학습된 필터를 활용하여 노이즈를 필터링하고 원본 이미지를 복원합니다. 본 논문에서는 컨볼루셔널 신경망을 기반으로 한 이미지 노이즈 제거 방법을 자세히 소개합니다. 1. 합성곱 신경망 개요 합성곱 신경망은 다중 합성곱 레이어, 풀링 레이어 및 완전 연결 레이어의 조합을 사용하여 이미지 특징을 학습하고 분류하는 딥러닝 알고리즘입니다. 컨볼루션 레이어에서는 컨볼루션 연산을 통해 이미지의 국소적 특징을 추출하여 이미지의 공간적 상관관계를 포착합니다. 풀링 레이어는 특징 차원을 줄여 계산량을 줄이고 주요 특징을 유지합니다. 완전 연결 계층은 학습된 특징과 레이블을 매핑하여 이미지 분류 또는 기타 작업을 구현하는 역할을 합니다. 이 네트워크 구조의 설계는 컨볼루션 신경망을 이미지 처리 및 인식에 유용하게 만듭니다.
 Rust를 사용하여 간단한 신경망을 작성하는 단계
Jan 23, 2024 am 10:45 AM
Rust를 사용하여 간단한 신경망을 작성하는 단계
Jan 23, 2024 am 10:45 AM
Rust는 안전, 성능 및 동시성에 초점을 맞춘 시스템 수준 프로그래밍 언어입니다. 운영 체제, 네트워크 애플리케이션, 임베디드 시스템과 같은 시나리오에 적합한 안전하고 신뢰할 수 있는 프로그래밍 언어를 제공하는 것을 목표로 합니다. Rust의 보안은 주로 소유권 시스템과 차용 검사기라는 두 가지 측면에서 비롯됩니다. 소유권 시스템을 사용하면 컴파일러는 컴파일 타임에 코드에서 메모리 오류를 확인할 수 있으므로 일반적인 메모리 안전 문제를 피할 수 있습니다. 컴파일 타임에 변수 소유권 이전을 강제로 검사함으로써 Rust는 메모리 자원이 적절하게 관리되고 해제되도록 보장합니다. 빌림 검사기는 변수의 수명 주기를 분석하여 동일한 변수가 여러 스레드에서 동시에 액세스되지 않도록 하여 일반적인 동시성 보안 문제를 방지합니다. 이 두 가지 메커니즘을 결합함으로써 Rust는 다음을 제공할 수 있습니다.
 트윈 신경망: 원리 및 응용 분석
Jan 24, 2024 pm 04:18 PM
트윈 신경망: 원리 및 응용 분석
Jan 24, 2024 pm 04:18 PM
Siamese Neural Network는 독특한 인공 신경망 구조입니다. 이는 동일한 매개변수와 가중치를 공유하는 두 개의 동일한 신경망으로 구성됩니다. 동시에 두 네트워크는 동일한 입력 데이터도 공유합니다. 이 디자인은 두 개의 신경망이 구조적으로 동일하기 때문에 쌍둥이에서 영감을 받았습니다. 샴 신경망의 원리는 두 입력 데이터 간의 유사성이나 거리를 비교하여 이미지 매칭, 텍스트 매칭, 얼굴 인식 등의 특정 작업을 완료하는 것입니다. 훈련 중에 네트워크는 유사한 데이터를 인접한 지역에 매핑하고 서로 다른 데이터를 먼 지역에 매핑하려고 시도합니다. 이러한 방식으로 네트워크는 서로 다른 데이터를 분류하거나 일치시키는 방법을 학습하여 해당 데이터를 달성할 수 있습니다.




