CUDA의 보편적인 행렬 곱셈: 입문부터 숙련까지!
GEMM(일반 행렬 곱셈)은 많은 응용 프로그램과 알고리즘의 중요한 부분이며 컴퓨터 하드웨어 성능을 평가하는 중요한 지표 중 하나이기도 합니다. GEMM 구현에 대한 심층적인 연구와 최적화는 고성능 컴퓨팅과 소프트웨어와 하드웨어 시스템 간의 관계를 더 잘 이해하는 데 도움이 될 수 있습니다. 컴퓨터 과학에서 GEMM의 효과적인 최적화는 컴퓨팅 속도를 높이고 리소스를 절약할 수 있으며, 이는 컴퓨터 시스템의 전반적인 성능을 향상시키는 데 중요합니다. GEMM의 작동 원리와 최적화 방법에 대한 심층적인 이해는 현대 컴퓨팅 하드웨어의 잠재력을 더 잘 활용하고 다양하고 복잡한 컴퓨팅 작업에 대한 보다 효율적인 솔루션을 제공하는 데 도움이 될 것입니다. GEMM의 성능을 최적화하고 개선함으로써 다음을 추가할 수 있습니다.
1. GEMM의 기본 특성
1.1 GEMM 계산 프로세스 및 복잡성
GEMM은 다음과 같이 정의됩니다.
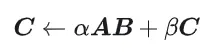

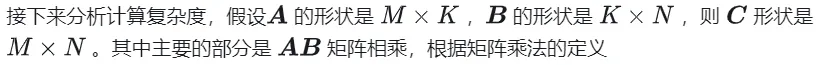
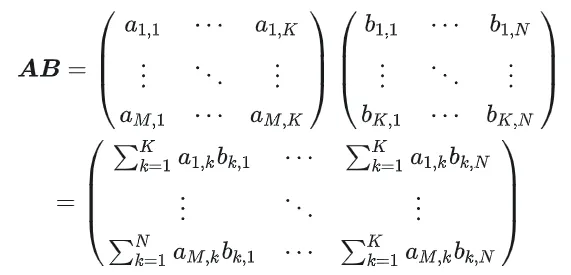


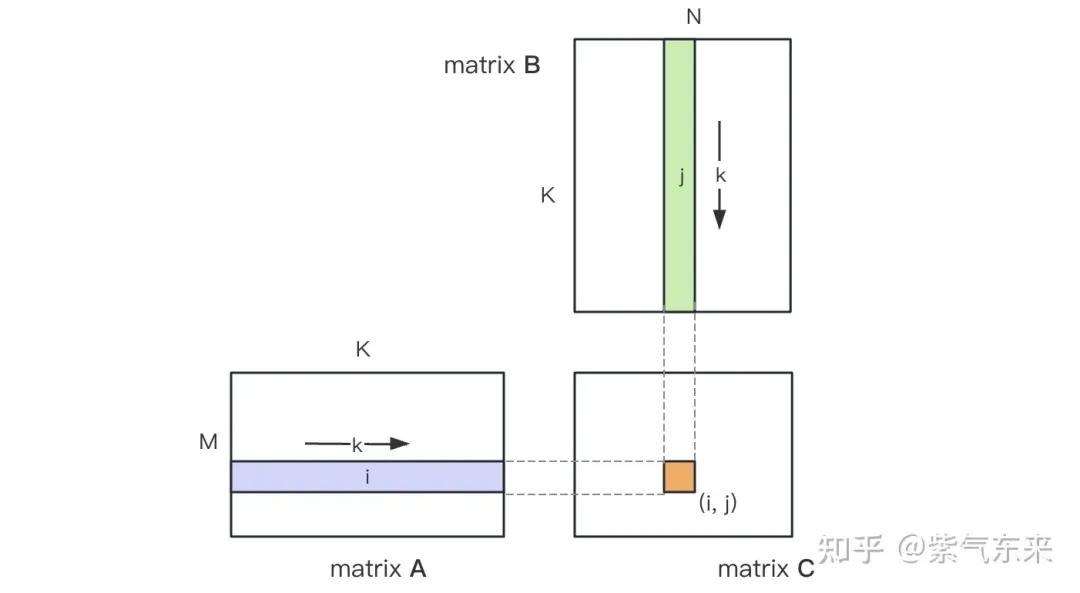
행렬 곱셈의 계산 다이어그램
1.2 간단한 구현 및 프로세스 분석
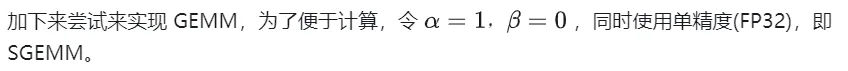
다음은 원래 정의에 따라 CPU에 구현된 코드이며 컨트롤로 사용됩니다. 정확성을 위해
#define OFFSET(row, col, ld) ((row) * (ld) + (col))void cpuSgemm(float *a, float *b, float *c, const int M, const int N, const int K) {for (int m = 0; m 다음은 CUDA를 사용하여 가장 간단한 행렬 곱셈인 Kernal을 구현합니다. 전체 행렬 곱셈을 완료하는 데 총 M * N 스레드가 사용됩니다. 각 스레드는 행렬 C의 요소 계산을 담당하며 K번의 곱셈과 누산을 완료해야 합니다. 행렬 A, B 및 C는 모두 전역 메모리에 저장됩니다(수정자 __global__ 에 의해 결정됨). 전체 코드는 sgemm_naive.cu를 참조하세요.
__global__ void naiveSgemm(float * __restrict__ a, float * __restrict__ b, float * __restrict__ c,const int M, const int N, const int K) {int n = blockIdx.x * blockDim.x + threadIdx.x;int m = blockIdx.y * blockDim.y + threadIdx.y;if (m 컴파일이 완료되었으며 Tesla V100-PCIE-32GB에서 실행한 결과는 다음과 같습니다. V100 백서에 따르면 FP32의 최대 컴퓨팅 파워는 15.7 TFLOPS이므로 이의 컴퓨팅 파워 활용도는 다음과 같습니다. 방법은 11.5%에 불과하다.
다음은 위 계산 프로세스의 워크플로를 자세히 분석하기 위한 예로 M=512, K=512, N=512를 사용합니다.
- 전역 메모리에서 행렬 A, B, C에 각각 저장 공간을 할당합니다.
- 행렬 때문에 C의 각 요소 계산은 서로 독립적이므로 병렬성 매핑에서 각 스레드는 행렬 C의 1 요소 계산에 해당합니다.
- 실행 구성의 GridSize와 blockSize는 모두 x를 갖습니다. (열 방향) , y (행 방향) 2차원, 그중


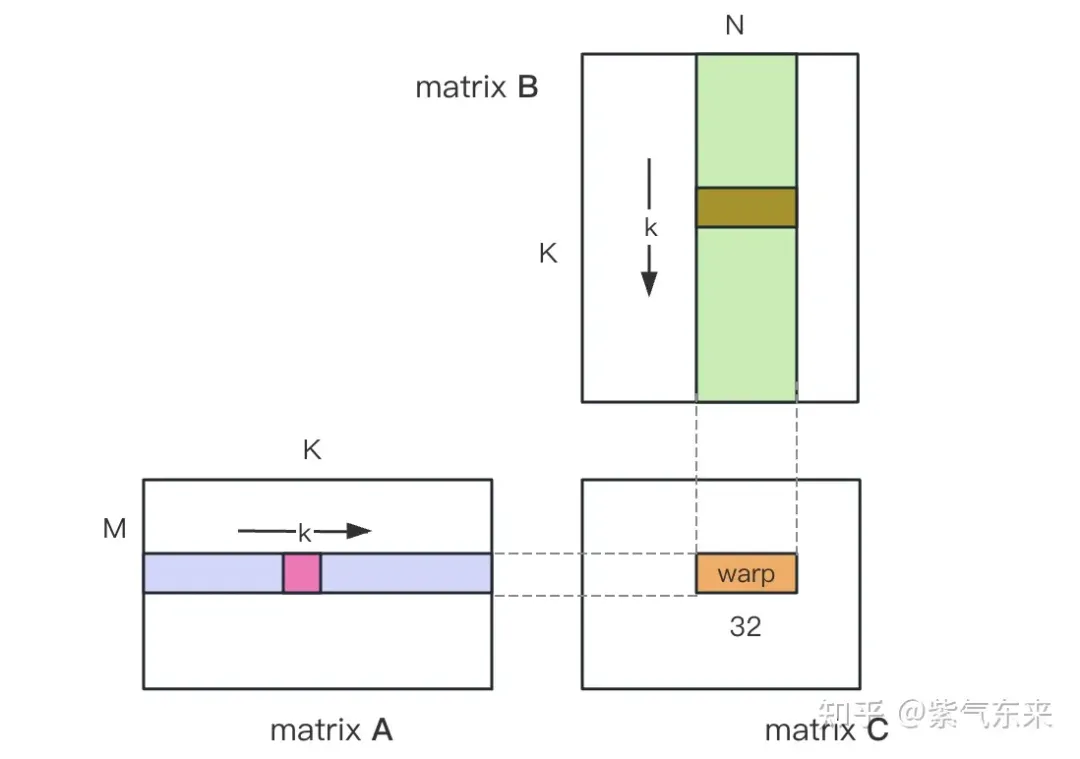


nsys는 순진한 프로파일링 버전을 기록합니다
2. GEMM 최적화 탐색
이전 기사에서는 단지 기능적인 GEMM만 구현했지만 성능은 기대와는 거리가 멀습니다. 이 섹션에서는 주로 GEMM 성능 최적화에 대해 연구합니다.
2.1 공유 메모리를 사용한 행렬 분할
위 계산에서는 곱셈 및 누산 작업을 완료하기 위해 두 개의 전역 메모리 로드가 필요합니다. 계산 메모리 액세스 비율이 매우 낮으며 효과적인 데이터 재사용이 없습니다. 따라서 공유 메모리를 사용하면 반복되는 메모리 읽기를 줄일 수 있습니다.
먼저 행렬 C를 BMxBN 크기의 동일한 블록으로 나눕니다. 각 블록은 블록으로 계산되며, 여기서 각 스레드는 행렬 C의 TMxTN 요소를 계산합니다. 그 후, 계산에 필요한 모든 데이터는 smem에서 읽혀지며, 이는 A 및 B 행렬의 반복적인 메모리 읽기의 일부를 제거합니다. 공유 메모리의 용량이 제한되어 있다는 점을 고려하면 BK 크기의 블록은 매번 K 차원으로 읽을 수 있습니다. 이러한 루프는 전체 행렬 곱셈 연산을 완료하는 데 총 K/BK 시간이 필요하며 블록의 결과를 얻을 수 있습니다. 프로세스는 아래 그림에 나와 있습니다.
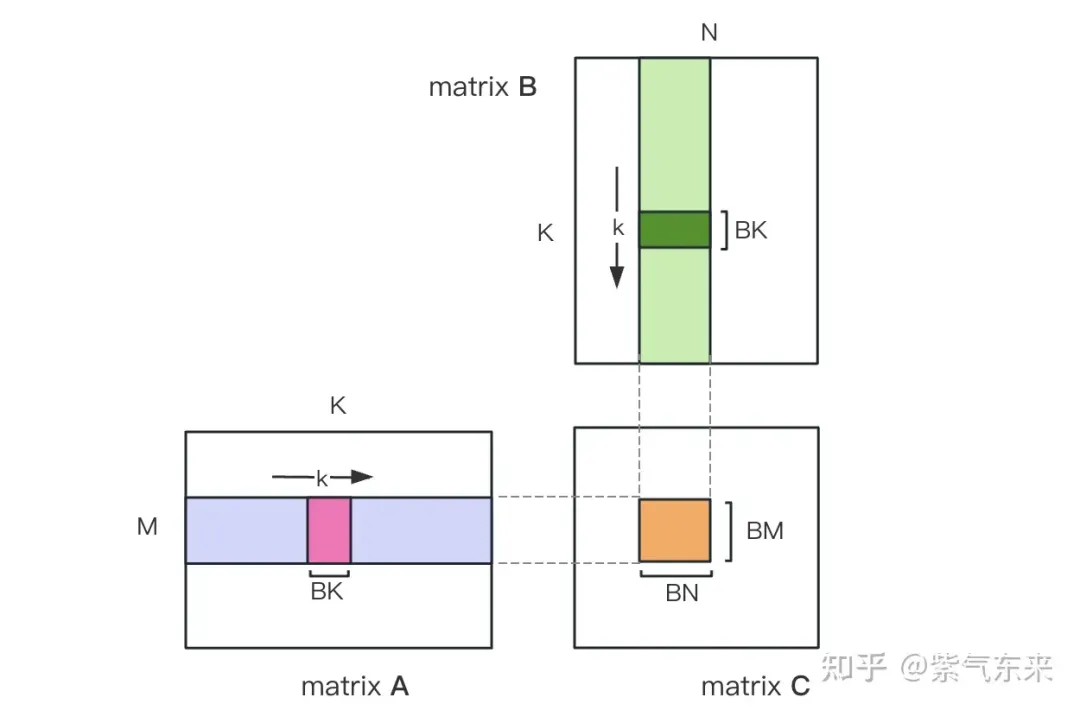
공유 메모리를 사용한 최적화 후 각 블록에 대해 다음을 얻을 수 있습니다.
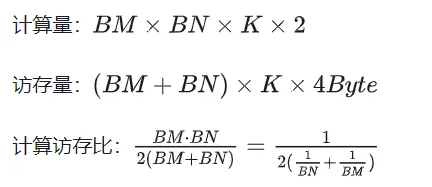
위 공식에서 BM과 BN이 클수록 계산 메모리 액세스 비율이 높을수록 성능이 향상됩니다. 그러나 공유 메모리 용량 제한(V100 1 SM은 96KB에 불과)으로 인해 블록은 BK * (BM + BN) * 4바이트를 차지해야 합니다.
TM과 TN의 값도 두 가지 측면에서 제한됩니다. 한편으로는 블록에 BM/TM *BN/TN 스레드가 있습니다. 1024를 초과하고 SM에 영향을 미치지 않도록 너무 높을 수는 없습니다. 반면에, 레지스터 수에는 제한이 있습니다. 스레드는 부분 합계를 저장하기 위해 최소한 TM * TN 레지스터가 필요합니다. 모든 레지스터 수는 256개를 초과할 수 없으며 동시에 SM의 병렬 스레드 수에 영향을 주지 않도록 너무 높을 수 없습니다.
마지막으로 BM = BN = 128, BK = 8, TM = TN = 8을 선택하면 계산된 메모리 액세스 비율은 32입니다. V100 15.7TFLOPS의 이론적 컴퓨팅 성능에 따르면 15.7TFLOPS/32 = 490GB/s를 얻을 수 있습니다. 측정된 HBM 대역폭은 763GB/s에 따르면 이 시점에서는 대역폭이 더 이상 컴퓨팅 성능을 제한하지 않는다는 것을 알 수 있습니다. 시간.
위 분석을 바탕으로 커널 함수 구현 프로세스는 다음과 같습니다. 전체 코드는 sgemm_v1.cu를 참조하세요. 주요 단계는 다음과 같습니다.
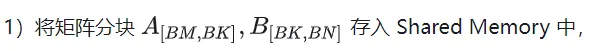

A B 행렬 분할의 스레드 인덱스 관계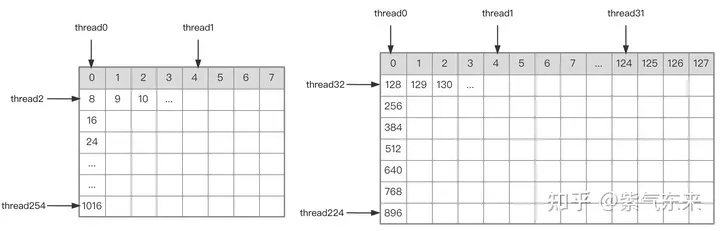
确定好单个block的执行过程,接下来需要确定多block处理的不同分块在Global Memory中的对应关系,仍然以A为例进行说明。由于分块沿着行的方向移动,那么首先需要确定行号,根据 Grid 的二维全局线性索引关系,by * BM 表示该分块的起始行号,同时我们已知load_a_smem_m 为分块内部的行号,因此全局的行号为load_a_gmem_m = by * BM + load_a_smem_m 。由于分块沿着行的方向移动,因此列是变化的,需要在循环内部计算,同样也是先计算起始列号bk * BK 加速分块内部列号load_a_smem_k 得到 load_a_gmem_k = bk * BK + load_a_smem_k ,由此我们便可以确定了分块在原始数据中的位置OFFSET(load_a_gmem_m, load_a_gmem_k, K) 。同理可分析矩阵分块 的情况,不再赘述。

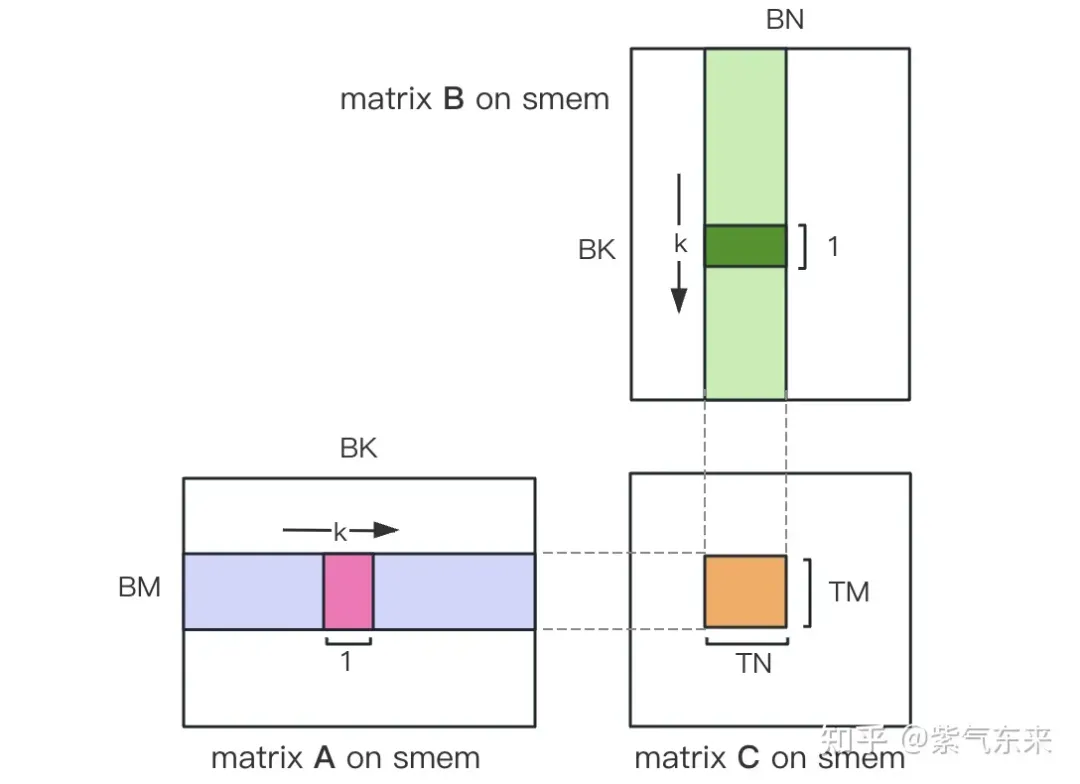
计算完后,还需要将其存入 Global Memory 中,这就需要计算其在 Global Memory 中的对应关系。由于存在更小的分块,则行和列均由3部分构成:全局行号store_c_gmem_m 等于大分块的起始行号by * BM+小分块的起始行号ty * TM+小分块内部的相对行号 i 。列同理。
__global__ void sgemm_V1(float * __restrict__ a, float * __restrict__ b, float * __restrict__ c,const int M, const int N, const int K) {const int BM = 128;const int BN = 128;const int BK = 8;const int TM = 8;const int TN = 8;const int bx = blockIdx.x;const int by = blockIdx.y;const int tx = threadIdx.x;const int ty = threadIdx.y;const int tid = ty * blockDim.x + tx;__shared__ float s_a[BM][BK];__shared__ float s_b[BK][BN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;// tid/2, row of s_aint load_a_smem_k = (tid & 1) > 5; // tid/32, row of s_bint load_b_smem_n = (tid & 31) 计算结果如下,性能达到了理论峰值性能的51.7%:
M N K =128128 1024, Time = 0.00031578 0.00031727 0.00032288 s, AVG Performance =98.4974 GflopsM N K =192192 1024, Time = 0.00031638 0.00031720 0.00031754 s, AVG Performance = 221.6661 GflopsM N K =256256 1024, Time = 0.00031488 0.00031532 0.00031606 s, AVG Performance = 396.4287 GflopsM N K =384384 1024, Time = 0.00031686 0.00031814 0.00032080 s, AVG Performance = 884.0425 GflopsM N K =512512 1024, Time = 0.00031814 0.00032007 0.00032493 s, AVG Performance =1562.1563 GflopsM N K =768768 1024, Time = 0.00032397 0.00034419 0.00034848 s, AVG Performance =3268.5245 GflopsM N K = 1024 1024 1024, Time = 0.00034570 0.00034792 0.00035331 s, AVG Performance =5748.3952 GflopsM N K = 1536 1536 1024, Time = 0.00068797 0.00068983 0.00069094 s, AVG Performance =6523.3424 GflopsM N K = 2048 2048 1024, Time = 0.00136173 0.00136552 0.00136899 s, AVG Performance =5858.5604 GflopsM N K = 3072 3072 1024, Time = 0.00271910 0.00273115 0.00274006 s, AVG Performance =6590.6331 GflopsM N K = 4096 4096 1024, Time = 0.00443805 0.00445964 0.00446883 s, AVG Performance =7175.4698 GflopsM N K = 6144 6144 1024, Time = 0.00917891 0.00950608 0.00996963 s, AVG Performance =7574.0999 GflopsM N K = 8192 8192 1024, Time = 0.01628838 0.01645271 0.01660790 s, AVG Performance =7779.8733 GflopsM N K =1228812288 1024, Time = 0.03592557 0.03597434 0.03614323 s, AVG Performance =8005.7066 GflopsM N K =1638416384 1024, Time = 0.06304122 0.06306373 0.06309302 s, AVG Performance =8118.7715 Gflops
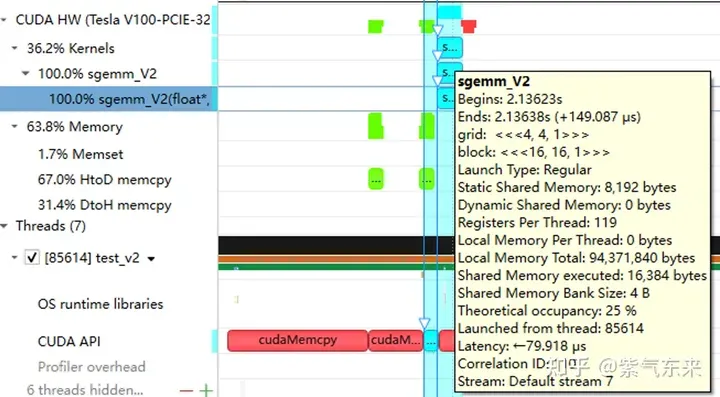
下面仍以M=512,K=512,N=512为例,分析一下结果。首先通过 profiling 可以看到 Shared Memory 占用为 8192 bytes,这与理论上(128+128)X8X4完全一致。
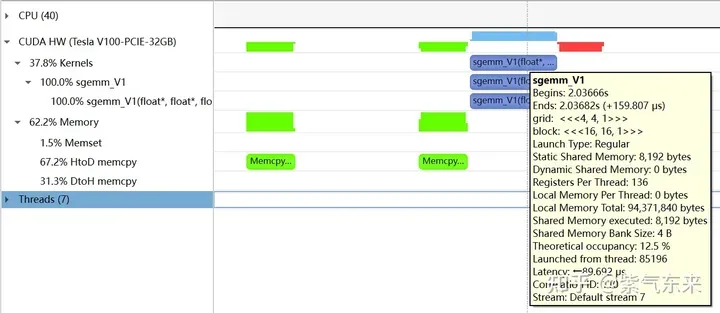 nsys 记录 的 V1 版本的 profiling
nsys 记录 的 V1 版本的 profiling
profiling 显示 Occupancy 为 12.5%,可以通过 cuda-calculator 加以印证,该例中 threads per block = 256, Registers per thread = 136, 由此可以计算得到每个SM中活跃的 warp 为8,而对于V100,每个SM中的 warp 总数为64,因此 Occupancy 为 8/64 = 12.5%。
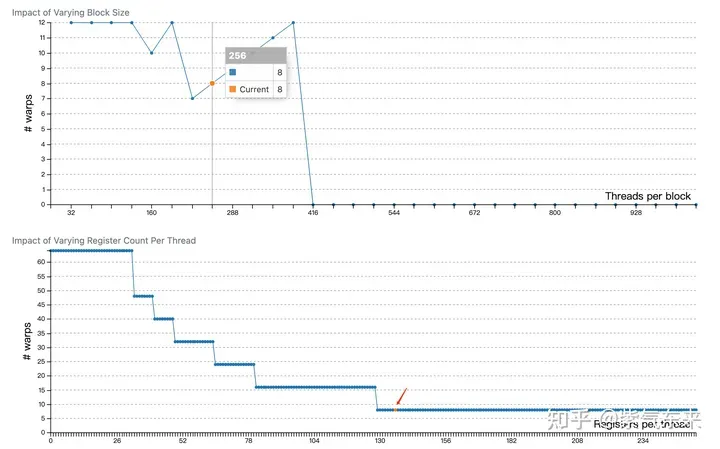
2.2 解决 Bank Conflict 问题
上节通过利用 Shared Memory 大幅提高了访存效率,进而提高了性能,本节将进一步优化 Shared Memory 的使用。
Shared Memory一共划分为32个Bank,每个Bank的宽度为4 Bytes,如果需要访问同一个Bank的多个数据,就会发生Bank Conflict。例如一个Warp的32个线程,如果访问的地址分别为0、4、8、...、124,就不会发生Bank Conflict,只占用Shared Memory一拍的时间;如果访问的地址为0、8、16、...、248,这样一来地址0和地址128对应的数据位于同一Bank、地址4和地址132对应的数据位于同一Bank,以此类推,那么就需要占用Shared Memory两拍的时间才能读出。
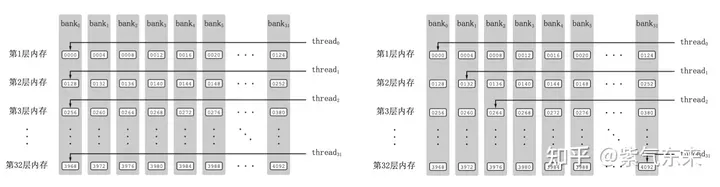
有 Bank Conflict VS 无 Bank Conflict
再看 V1 版本计算部分的三层循环,每次从Shared memory中取矩阵A的长度为TM的向量和矩阵B的长度为TN的向量,这两个向量做外积并累加到部分和中,一次外积共TM * TN次乘累加,一共需要循环BK次取数和外积。
接下来分析从Shared Memory load的过程中存在的Bank Conflict:
i) 取矩阵A需要取一个列向量,而矩阵A在Shared Memory中是按行存储的;
ii) 在TM = TN = 8的情况下,无论矩阵A还是矩阵B,从Shared Memory中取数时需要取连续的8个数,即便用LDS.128指令一条指令取四个数,也需要两条指令,由于一个线程的两条load指令的地址是连续的,那么同一个Warp不同线程的同一条load指令的访存地址就是被间隔开的,便存在着 Bank Conflict。
为了解决上述的两点Shared Memory的Bank Conflict,采用了一下两点优化:
i) 为矩阵A分配Shared Memory时形状分配为[BK][BM],即让矩阵A在Shared Memory中按列存储
ii) 将原本每个线程负责计算的TM * TN的矩阵C,划分为下图中这样的两块TM/2 * TN的矩阵C,由于TM/2=4,一条指令即可完成A的一块的load操作,两个load可同时进行。
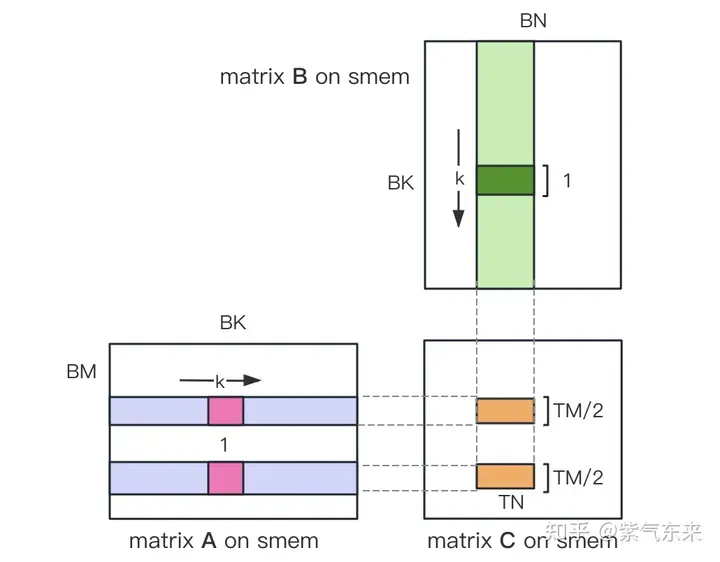
kernel 函数的核心部分实现如下,完整代码见 sgemm_v2.cu 。
__shared__ float s_a[BK][BM];__shared__ float s_b[BK][BN];float r_load_a[4];float r_load_b[4];float r_comp_a[TM];float r_comp_b[TN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;int load_a_smem_k = (tid & 1) > 5;int load_b_smem_n = (tid & 31) 结果如下,相对未解决 Bank Conflict 版(V1) 性能提高了 14.4%,达到了理论峰值的74.3%。
M N K =128128 1024, Time = 0.00029699 0.00029918 0.00030989 s, AVG Performance = 104.4530 GflopsM N K =192192 1024, Time = 0.00029776 0.00029828 0.00029882 s, AVG Performance = 235.7252 GflopsM N K =256256 1024, Time = 0.00029485 0.00029530 0.00029619 s, AVG Performance = 423.2949 GflopsM N K =384384 1024, Time = 0.00029734 0.00029848 0.00030090 s, AVG Performance = 942.2843 GflopsM N K =512512 1024, Time = 0.00029853 0.00029945 0.00030070 s, AVG Performance =1669.7479 GflopsM N K =768768 1024, Time = 0.00030458 0.00032467 0.00032790 s, AVG Performance =3465.1038 GflopsM N K = 1024 1024 1024, Time = 0.00032406 0.00032494 0.00032621 s, AVG Performance =6155.0281 GflopsM N K = 1536 1536 1024, Time = 0.00047990 0.00048224 0.00048461 s, AVG Performance =9331.3912 GflopsM N K = 2048 2048 1024, Time = 0.00094426 0.00094636 0.00094992 s, AVG Performance =8453.4569 GflopsM N K = 3072 3072 1024, Time = 0.00187866 0.00188096 0.00188538 s, AVG Performance =9569.5816 GflopsM N K = 4096 4096 1024, Time = 0.00312589 0.00319050 0.00328147 s, AVG Performance = 10029.7885 GflopsM N K = 6144 6144 1024, Time = 0.00641280 0.00658940 0.00703498 s, AVG Performance = 10926.6372 GflopsM N K = 8192 8192 1024, Time = 0.01101130 0.01116194 0.01122950 s, AVG Performance = 11467.5446 GflopsM N K =1228812288 1024, Time = 0.02464854 0.02466705 0.02469344 s, AVG Performance = 11675.4946 GflopsM N K =1638416384 1024, Time = 0.04385955 0.04387468 0.04388355 s, AVG Performance = 11669.5995 Gflops
分析一下 profiling 可以看到 Static Shared Memory 仍然是使用了8192 Bytes,奇怪的的是,Shared Memory executed 却翻倍变成了 16384 Bytes(知友如果知道原因可以告诉我一下)。
2.3 流水并行化:Double Buffering
Double Buffering,即双缓冲,即通过增加buffer的方式,使得 访存-计算 的串行模式流水线化,以减少等待时间,提高计算效率,其原理如下图所示:
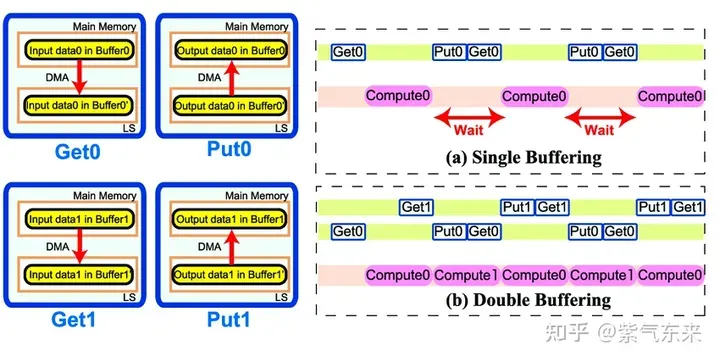
Single Buffering VS Double Buffering
具体到 GEMM 任务中来,就是需要两倍的Shared Memory,之前只需要BK * (BM + BN) * 4 Bytes的Shared Memory,采用Double Buffering之后需要2BK * (BM + BN) * 4 Bytes的Shared Memory,然后使其 pipeline 流动起来。
代码核心部分如下所示,完整代码参见 sgemm_v3.cu 。有以下几点需要注意:
1)主循环从bk = 1 开始,第一次数据加载在主循环之前,最后一次计算在主循环之后,这是pipeline 的特点决定的;
2)由于计算和下一次访存使用的Shared Memory不同,因此主循环中每次循环只需要一次__syncthreads()即可
3)由于GPU不能向CPU那样支持乱序执行,主循环中需要先将下一次循环计算需要的Gloabal Memory中的数据load 到寄存器,然后进行本次计算,之后再将load到寄存器中的数据写到Shared Memory,这样在LDG指令向Global Memory做load时,不会影响后续FFMA及其它运算指令的 launch 执行,也就达到了Double Buffering的目的。
__shared__ float s_a[2][BK][BM];__shared__ float s_b[2][BK][BN];float r_load_a[4];float r_load_b[4];float r_comp_a[TM];float r_comp_b[TN];float r_c[TM][TN] = {0.0};int load_a_smem_m = tid >> 1;int load_a_smem_k = (tid & 1) > 5;int load_b_smem_n = (tid & 31) 性能如下所示,达到了理论峰值的 80.6%。
M N K =128128 1024, Time = 0.00024000 0.00024240 0.00025792 s, AVG Performance = 128.9191 GflopsM N K =192192 1024, Time = 0.00024000 0.00024048 0.00024125 s, AVG Performance = 292.3840 GflopsM N K =256256 1024, Time = 0.00024029 0.00024114 0.00024272 s, AVG Performance = 518.3728 GflopsM N K =384384 1024, Time = 0.00024070 0.00024145 0.00024198 s, AVG Performance =1164.8394 GflopsM N K =512512 1024, Time = 0.00024173 0.00024237 0.00024477 s, AVG Performance =2062.9786 GflopsM N K =768768 1024, Time = 0.00024291 0.00024540 0.00026010 s, AVG Performance =4584.3820 GflopsM N K = 1024 1024 1024, Time = 0.00024534 0.00024631 0.00024941 s, AVG Performance =8119.7302 GflopsM N K = 1536 1536 1024, Time = 0.00045712 0.00045780 0.00045872 s, AVG Performance =9829.5167 GflopsM N K = 2048 2048 1024, Time = 0.00089632 0.00089970 0.00090656 s, AVG Performance =8891.8924 GflopsM N K = 3072 3072 1024, Time = 0.00177891 0.00178289 0.00178592 s, AVG Performance = 10095.9883 GflopsM N K = 4096 4096 1024, Time = 0.00309763 0.00310057 0.00310451 s, AVG Performance = 10320.6843 GflopsM N K = 6144 6144 1024, Time = 0.00604826 0.00619887 0.00663078 s, AVG Performance = 11615.0253 GflopsM N K = 8192 8192 1024, Time = 0.01031738 0.01045051 0.01048861 s, AVG Performance = 12248.2036 GflopsM N K =1228812288 1024, Time = 0.02283978 0.02285837 0.02298272 s, AVG Performance = 12599.3212 GflopsM N K =1638416384 1024, Time = 0.04043287 0.04044823 0.04046151 s, AVG Performance = 12658.1556 Gflops
从 profiling 可以看到双倍的 Shared Memory 的占用

三、cuBLAS 实现方式探究
本节我们将认识CUDA的标准库——cuBLAS, 即NVIDIA版本的基本线性代数子程序 (Basic Linear Algebra Subprograms, BLAS) 规范实现代码。它支持 Level 1 (向量与向量运算) ,Level 2 (向量与矩阵运算) ,Level 3 (矩阵与矩阵运算) 级别的标准矩阵运算。
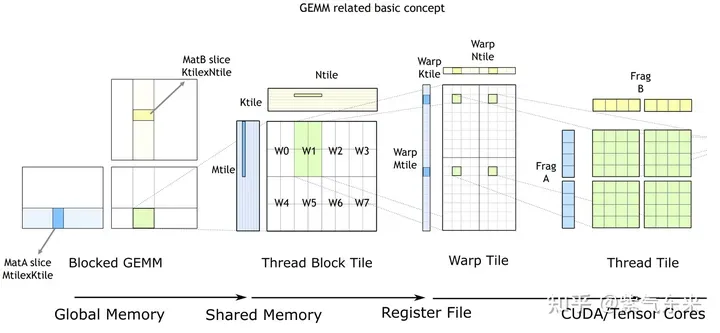
cuBLAS/CUTLASS GEMM的基本过程
如上图所示,计算过程分解成线程块片(thread block tile)、线程束片(warp tile)和线程片(thread tile)的层次结构并将AMP的策略应用于此层次结构来高效率的完成基于GPU的拆分成tile的GEMM。这个层次结构紧密地反映了NVIDIA CUDA编程模型。可以看到从global memory到shared memory的数据移动(矩阵到thread block tile);从shared memory到寄存器的数据移动(thread block tile到warp tile);从寄存器到CUDA core的计算(warp tile到thread tile)。
cuBLAS 实现了单精度矩阵乘的函数cublasSgemm,其主要参数如下:
cublasStatus_t cublasSgemm( cublasHandle_t handle, // 调用 cuBLAS 库时的句柄 cublasOperation_t transa, // A 矩阵是否需要转置 cublasOperation_t transb, // B 矩阵是否需要转置 int m, // A 的行数 int n, // B 的列数 int k, // A 的列数 const float *alpha, // 系数 α, host or device pointer const float *A, // 矩阵 A 的指针,device pointer int lda, // 矩阵 A 的主维,if A 转置, lda = max(1, k), else max(1, m) const float *B, // 矩阵 B 的指针, device pointer int ldb, // 矩阵 B 的主维,if B 转置, ldb = max(1, n), else max(1, k) const float *beta, // 系数 β, host or device pointer float *C, // 矩阵 C 的指针,device pointer int ldc // 矩阵 C 的主维,ldc >= max(1, m) );
调用方式如下:
cublasHandle_t cublas_handle;cublasCreate(&cublas_handle);float cublas_alpha = 1.0;float cublas_beta = 0;cublasSgemm(cublas_handle, CUBLAS_OP_N, CUBLAS_OP_N, N, M, K, &cublas_alpha, d_b, N, d_a, K, &cublas_beta, d_c, N);
性能如下所示,达到了理论峰值的 82.4%。
M N K =128128 1024, Time = 0.00002704 0.00003634 0.00010822 s, AVG Performance = 860.0286 GflopsM N K =192192 1024, Time = 0.00003155 0.00003773 0.00007267 s, AVG Performance =1863.6689 GflopsM N K =256256 1024, Time = 0.00003917 0.00004524 0.00007747 s, AVG Performance =2762.9438 GflopsM N K =384384 1024, Time = 0.00005318 0.00005978 0.00009120 s, AVG Performance =4705.0655 GflopsM N K =512512 1024, Time = 0.00008326 0.00010280 0.00013840 s, AVG Performance =4863.9646 GflopsM N K =768768 1024, Time = 0.00014278 0.00014867 0.00018816 s, AVG Performance =7567.1560 GflopsM N K = 1024 1024 1024, Time = 0.00023485 0.00024460 0.00028150 s, AVG Performance =8176.5614 GflopsM N K = 1536 1536 1024, Time = 0.00046474 0.00047607 0.00051181 s, AVG Performance =9452.3201 GflopsM N K = 2048 2048 1024, Time = 0.00077930 0.00087862 0.00092307 s, AVG Performance =9105.2126 GflopsM N K = 3072 3072 1024, Time = 0.00167904 0.00168434 0.00171114 s, AVG Performance = 10686.6837 GflopsM N K = 4096 4096 1024, Time = 0.00289619 0.00291068 0.00295904 s, AVG Performance = 10994.0128 GflopsM N K = 6144 6144 1024, Time = 0.00591766 0.00594586 0.00596915 s, AVG Performance = 12109.2611 GflopsM N K = 8192 8192 1024, Time = 0.01002384 0.01017465 0.01028435 s, AVG Performance = 12580.2896 GflopsM N K =1228812288 1024, Time = 0.02231159 0.02233805 0.02245619 s, AVG Performance = 12892.7969 GflopsM N K =1638416384 1024, Time = 0.03954650 0.03959291 0.03967242 s, AVG Performance = 12931.6086 Gflops
由此可以对比以上各种方法的性能情况,可见手动实现的性能已接近于官方的性能,如下:
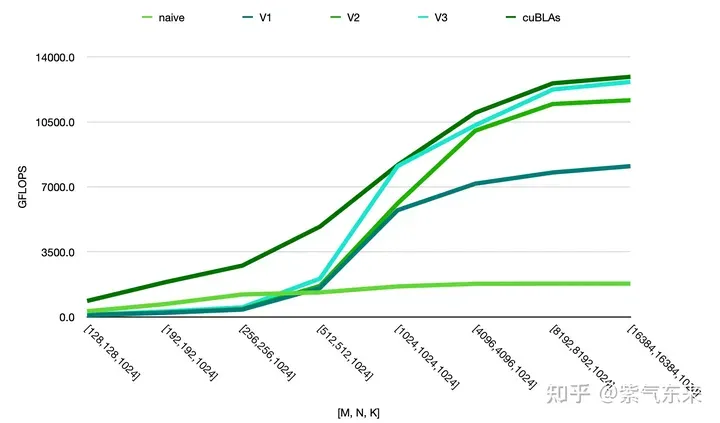
위 내용은 CUDA의 보편적인 행렬 곱셈: 입문부터 숙련까지!의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!

핫 AI 도구

Undresser.AI Undress
사실적인 누드 사진을 만들기 위한 AI 기반 앱

AI Clothes Remover
사진에서 옷을 제거하는 온라인 AI 도구입니다.

Undress AI Tool
무료로 이미지를 벗다

Clothoff.io
AI 옷 제거제

AI Hentai Generator
AI Hentai를 무료로 생성하십시오.

인기 기사

뜨거운 도구

메모장++7.3.1
사용하기 쉬운 무료 코드 편집기

SublimeText3 중국어 버전
중국어 버전, 사용하기 매우 쉽습니다.

스튜디오 13.0.1 보내기
강력한 PHP 통합 개발 환경

드림위버 CS6
시각적 웹 개발 도구

SublimeText3 Mac 버전
신 수준의 코드 편집 소프트웨어(SublimeText3)

뜨거운 주제
 7478
7478
 15
15
 1377
1377
 52
52
 77
77
 11
11
 50
50
 19
19
 19
19
 33
33
 2018-2024 USD의 Bitcoin의 최신 가격
Feb 15, 2025 pm 07:12 PM
2018-2024 USD의 Bitcoin의 최신 가격
Feb 15, 2025 pm 07:12 PM
실시간 비트 코인 USD 가격 비트 코인 가격에 영향을 미치는 요인 향후 비트 코인 가격을 예측하기위한 지표 다음은 2018-2024 년 비트 코인 가격에 대한 몇 가지 주요 정보입니다.
 GO의 어떤 라이브러리가 대기업에서 개발하거나 잘 알려진 오픈 소스 프로젝트에서 제공합니까?
Apr 02, 2025 pm 04:12 PM
GO의 어떤 라이브러리가 대기업에서 개발하거나 잘 알려진 오픈 소스 프로젝트에서 제공합니까?
Apr 02, 2025 pm 04:12 PM
GO의 어떤 라이브러리가 대기업이나 잘 알려진 오픈 소스 프로젝트에서 개발 했습니까? GO에 프로그래밍 할 때 개발자는 종종 몇 가지 일반적인 요구를 만납니다.
 C 언어로 멀티 스레딩을 구현하는 4 가지 방법
Apr 03, 2025 pm 03:00 PM
C 언어로 멀티 스레딩을 구현하는 4 가지 방법
Apr 03, 2025 pm 03:00 PM
언어의 멀티 스레딩은 프로그램 효율성을 크게 향상시킬 수 있습니다. C 언어에서 멀티 스레딩을 구현하는 4 가지 주요 방법이 있습니다. 독립 프로세스 생성 : 여러 독립적으로 실행되는 프로세스 생성, 각 프로세스에는 자체 메모리 공간이 있습니다. 의사-다일리트 레딩 : 동일한 메모리 공간을 공유하고 교대로 실행하는 프로세스에서 여러 실행 스트림을 만듭니다. 멀티 스레드 라이브러리 : PTHREADS와 같은 멀티 스레드 라이브러리를 사용하여 스레드를 만들고 관리하여 풍부한 스레드 작동 기능을 제공합니다. COROUTINE : 작업을 작은 하위 작업으로 나누고 차례로 실행하는 가벼운 다중 스레드 구현.
 C 언어로 일반적으로 사용되는 합계는 무엇입니까?
Apr 03, 2025 pm 02:39 PM
C 언어로 일반적으로 사용되는 합계는 무엇입니까?
Apr 03, 2025 pm 02:39 PM
C 언어 표준 라이브러리에는 "sum"이라는 기능이 없습니다. "합"은 일반적으로 프로그래머에 의해 정의되거나 특정 라이브러리에서 제공되며 기능은 특정 구현에 따라 다릅니다. 일반적인 시나리오는 배열에 대한 요약되며 링크 된 목록과 같은 다른 데이터 구조에서도 사용할 수 있습니다. 또한 "Sum"은 이미지 처리 및 통계 분석과 같은 필드에서도 사용됩니다. 탁월한 "합"기능은 가독성, 견고성 및 효율성이 우수해야합니다.
 CSS를 통해 크기 조정 기호를 사용자 정의하고 배경색으로 균일하게 만드는 방법은 무엇입니까?
Apr 05, 2025 pm 02:30 PM
CSS를 통해 크기 조정 기호를 사용자 정의하고 배경색으로 균일하게 만드는 방법은 무엇입니까?
Apr 05, 2025 pm 02:30 PM
CSS에서 크기 조정 기호를 사용자 정의하는 방법은 배경색으로 통합됩니다. 매일 개발에서, 우리는 종종 조정과 같은 사용자 인터페이스 세부 정보를 사용자 정의 해야하는 상황을 발생시킵니다.
 H5 페이지 제작은 프론트 엔드 개발입니까?
Apr 05, 2025 pm 11:42 PM
H5 페이지 제작은 프론트 엔드 개발입니까?
Apr 05, 2025 pm 11:42 PM
예, H5 페이지 제작은 HTML, CSS 및 JavaScript와 같은 핵심 기술을 포함하는 프론트 엔드 개발을위한 중요한 구현 방법입니다. 개발자는 & lt; canvas & gt; 그래픽을 그리거나 상호 작용 동작을 제어하기 위해 JavaScript를 사용하는 태그.
 CSS의 클립 경로 속성을 사용하여 세그먼터의 45도 곡선 효과를 달성하는 방법은 무엇입니까?
Apr 04, 2025 pm 11:45 PM
CSS의 클립 경로 속성을 사용하여 세그먼터의 45도 곡선 효과를 달성하는 방법은 무엇입니까?
Apr 04, 2025 pm 11:45 PM
세그먼터의 45도 곡선 효과를 달성하는 방법은 무엇입니까? 세분화 장치를 구현하는 과정에서 왼쪽 버튼을 클릭 할 때 오른쪽 테두리를 45도 곡선으로 바꾸는 방법과 포인트 ...
 플렉스 레이아웃 아래의 텍스트는 생략되지만 컨테이너가 열려 있습니까? 그것을 해결하는 방법?
Apr 05, 2025 pm 11:00 PM
플렉스 레이아웃 아래의 텍스트는 생략되지만 컨테이너가 열려 있습니까? 그것을 해결하는 방법?
Apr 05, 2025 pm 11:00 PM
Flex 레이아웃 및 솔루션에서 텍스트를 과도하게 누락하여 컨테이너 개구부 문제가 사용됩니다 ...




