Google 블로그에서는 무방향 그래프의 최소 절단 문제를 해결하기 위한 새로운 연구를 발표했습니다.
1996년 미국의 컴퓨터 과학자 David R Karger와 다른 연구자들은 "최소 컷 문제에 대한 새로운 접근 방식"이라는 논문에서 놀라운 무작위 알고리즘 Karger의 알고리즘을 제안했는데, 이는 이론 컴퓨터 과학에서 매우 인기가 높습니다. 매우 중요하며 특히 대규모 그래프의 대략적인 최소 절단 문제에 적합합니다. Karger의 알고리즘은 시간 O(m log^3n)에서 그래프의 최소 절단점을 찾을 수 있습니다. 이는 거의 선형 시간이라고 하며 이는 다대수 인자에 의한 선형 곱셈을 의미합니다. Google이 최근 업데이트한 블로그에서 이전에 출판된 논문 "Deterministic Near-Linear Time Minimum Cut in Weighted Graphs"를 소개했으며 해당 연구는 ACM-SIAM SODA24 최우수 논문상을 수상했습니다. 이 기사에서는 (선형에 가까운 시간이 아닌) 거의 선형적인 시간에 실행되는 새로운 알고리즘에 대해 자세히 설명합니다. 이 알고리즘은 결정적이며 올바른 최소 컷을 안정적으로 찾을 수 있으며 정확하다고 보장할 수 없거나 적용할 수만 있는 이전 알고리즘을 개선합니다. 간단한 그래프를 위한 알고리즘. 틀림없이 이것은 Karger의 유명한 무작위화 알고리즘 이후 가장 큰 발견입니다.
- 논문 주소: https://arxiv.org/pdf/2401.05627.pdf
- 논문 제목: 가중 그래프의 결정적 근사 선형 시간 최소 컷
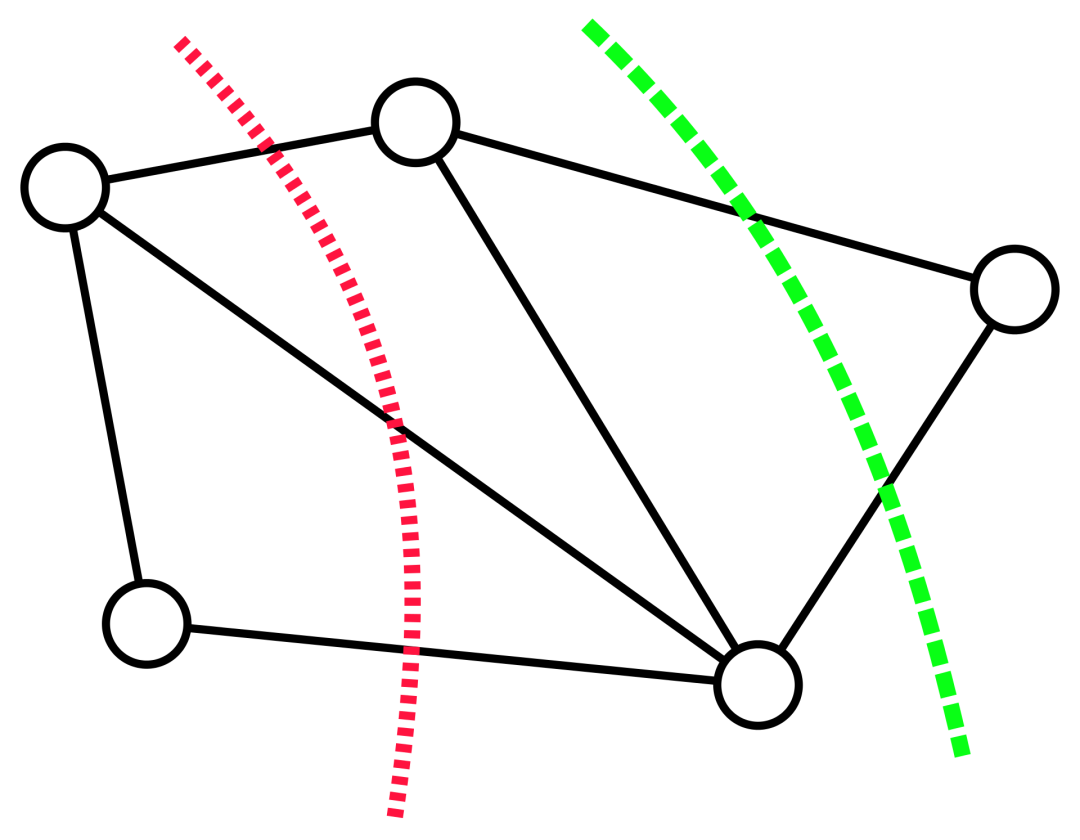
참고: 가장 작음 컷 문제(종종 최소 컷이라고도 함)는 그래프 연결에 대한 기본적인 구조적 문제로, 일반적으로 네트워크 연결을 끊는 가장 간단한 방법이 무엇인지에 중점을 둡니다. 그래프 이론에서는 모든 간선을 제거하여 네트워크 흐름 그래프를 더 이상 연결되지 않게(즉, 두 개의 하위 그래프로 나누기) 할 수 있는 간선 집합을 그래프의 컷이라고 하며, 그래프에서 가장 작은 컷을 그래프의 컷이라고 합니다. 최소 컷. ㅋㅋㅋ ~ 그래프와 두 개의 컷: 빨간색 점선은 세 개의 가장자리를 포함하는 컷을 표시하고 녹색 점선은 이 그래프의 최소 컷(두 개의 가장자리 포함)을 나타냅니다. 최소 컷 문제와 관련하여 Karger는 1996년에 거의 선형에 가까운 시간 무작위 알고리즘을 개척했는데, 이는 높은 확률로 최소 컷을 찾을 수 있으며, 이 연구는 또한 모든 컷의 크기를 크게 유지하는 더 작은 그래프가 존재한다는 주요 통찰력이 있습니다.
이 발견은 더 작은 그래프를 입력으로 사용하여 더 느린 알고리즘을 실행할 수 있고 더 느린 실행 시간(더 작은 그래프의 크기 측면에서)이 여전히 원본(더 큰)과 비슷하기 때문에 유용합니다. 그래프는 거의 선형입니다.
실제로 최소 절단 문제에 대한 많은 구조적 발견이 이 방향을 따라 수행됩니다.
Google은 n개의 노드가 있는 그래프 G에서 시작하여 "Randomized Approximation Schemes for Cuts and Flows in Capacitated Graphs"(Benzur, Karger 저작) 논문에서 제안된 절단 보존 희소성 방법을 기반으로 이 작업을 수행합니다. ) 는 더 적은 수의 간선을 가진 희소 가중치 그래프 G'를 구성할 수 있음을 증명하며, 이 그래프에서 거의 모든 컷의 크기는 원본 그래프 G의 해당 컷 크기와 대략 동일합니다.
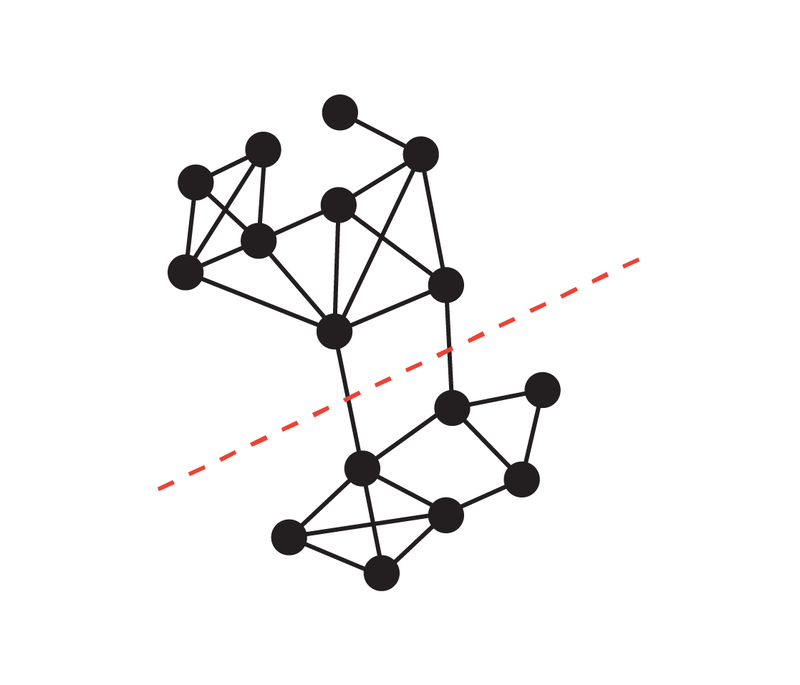
이 개념은 다음 예에서 설명할 수 있습니다. 원본 그래프는 단일 간선으로 연결된 두 개의 완전한 그래프로 구성되는 반면 희소화된 그래프는 간선 수가 적지만 간선 가중치는 더 크고 모든 컷의 크기는 다음과 같습니다. 대충 보존됨. 이 희소 그래프를 구성하기 위해 Benzur와 Karger는 독립적으로 가장자리를 샘플링하는 방법을 채택했습니다. 이 방법에서는 그래프 G의 각 간선이 그래프 G'에 포함될 확률이 일정하며, G'의 가중치는 샘플링 확률의 역수에 따라 증폭됩니다(예를 들어 간선의 원래 가중치가 다음과 같은 경우). 1 Edge는 10%의 확률로 포함되며, 가중치는 10으로 조정됩니다. 이 매우 간단한(거의 선형 시간) 방법은 높은 성공 확률로 절단 보존 그래프 희소화를 구성할 수 있다는 것이 밝혀졌습니다. Karger 알고리즘은 몬테카를로 알고리즘입니다. 즉, 작은 확률로 출력이 정확하지 않을 수 있으며, 실제 알려진 최소 컷과 비교하는 것 외에는 출력이 올바른지 알 수 있는 알려진 방법이 없습니다. . 따라서 연구자들은 선형에 가까운 시간 결정론적 알고리즘의 미해결 문제를 해결하는 방법을 모색하기 위해 열심히 노력해 왔습니다. 절단 보존 그래프 희소화의 구성은 Karger 알고리즘의 유일한 확률적 구성 요소이므로 한 가지 접근 방식은 거의 선형 시간에 희소화의 결정론적 구성을 찾는 것입니다(비무작위화라고도 함). 2015년에 Kawarabayashi와 Thorup은 간단한 그래프(즉, 각 노드 쌍 사이에 최대 하나의 간선이 있고 모든 간선 가중치가 1인 그래프)에 대한 결정론적 근선형 시간 알고리즘을 찾는 중요한 이정표를 달성했습니다. 이 연구는 최소 컷과 또 다른 중요한 그래프 구조("낮은 컨덕턴스 컷"이라고 함) 사이에 몇 가지 연결이 있다는 핵심 아이디어로 이어집니다. 이 연결은 나중에 일반 가장자리 가중치 그래프에서 Karger의 알고리즘을 무작위화하지 않는 데 중요했으며 Google이 새로운 알고리즘을 도출하는 데 도움이 되었습니다. 그래프 컷 S의 컨덕턴스는 S의 컷 크기와 S의 부피의 비율로 정의됩니다(S를 컷의 볼륨 쪽이 더 작고 비어 있지 않음), 여기서 S의 볼륨은 S의 노드 정도입니다. 컷 S의 낮은 컨덕턴스 S는 S를 그래프의 나머지 부분에 연결하는 (볼륨에 비해) 소수의 가장자리만 있기 때문에 네트워크의 병목 현상을 직관적으로 포착합니다. 그래프의 컨덕턴스는 그래프의 어떤 컷에 대한 최소 컨덕턴스로 정의되며, 컨덕턴스가 큰 그래프(확장 그래프라고도 함)는 내부에 병목 현상이 없기 때문에 잘 연결되었다고 합니다. ㅋㅋㅋ Kawayabarashi와 Thorup은 최소 노드 차수가 큰 간단한 그래프에서 중요하지 않은(즉, 양쪽에 최소 2개의 노드) 최소 컷은 전도도가 낮아야 함을 관찰했습니다. 이러한 관찰을 바탕으로 그래프를 잘 연결된 클러스터로 분할할 수 있는 경우 모든 클러스터는 모든 컷의 한 쪽에 정확히 놓여야 하므로 분할은 모든 중요하지 않은 최소 컷과 일관되어야 합니다. 그런 다음 각 클러스터는 노드로 축소되고 원본 그래프의 모든 사소한 최소 컷이 그대로 유지되는 더 작은 그래프가 처리됩니다.
그러나 가중치 그래프의 경우 위의 관찰은 더 이상 유지되지 않으며 단순 그래프 사례에 사용된 동일한 분할이 사소하지 않은 최소 절단과 정확하게 일치하지 않을 수 있습니다.
아래 그림에서 볼 수 있듯이 Jason Li는 2021년에 이 구분이 여전히 사소하지 않은 최소 삭감과 대략적으로 일치한다는 것을 관찰했습니다. 특히, 중요하지 않은 최소 컷 S의 경우 S'가 클러스터와 일치하도록 S와 유사한 컷 S'가 있습니다. Jason Li는 이러한 분할 속성을 활용하여 절단 보존 그래프 희소성의 구성을 효과적으로 비무작위화할 수 있음을 추가로 관찰했습니다.
Google이 설계한 새로운 알고리즘은 min-cut의 사용 사례를 공식화하기 위해 파티션을 구성하는 것을 목표로 합니다. Google 연구는 Jason Li가 이전 연구에서 사용한 보다 일반적인 기성 방법보다 더 정확하고 빠릅니다. 새로운 연구는 정확성을 보장하면서 실행 시간을 최적화하고 최종적으로 최소 절단 문제에 대한 선형에 가까운 시간 결정론적 알고리즘을 실현했습니다.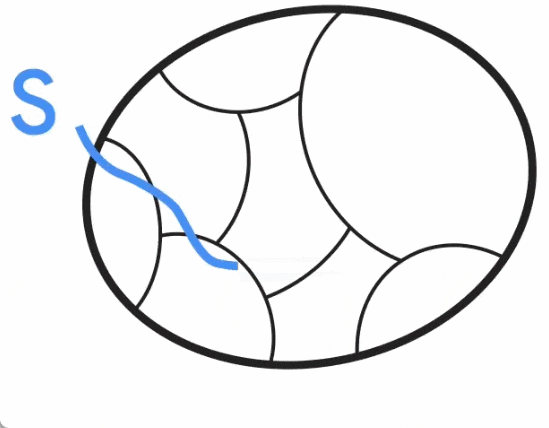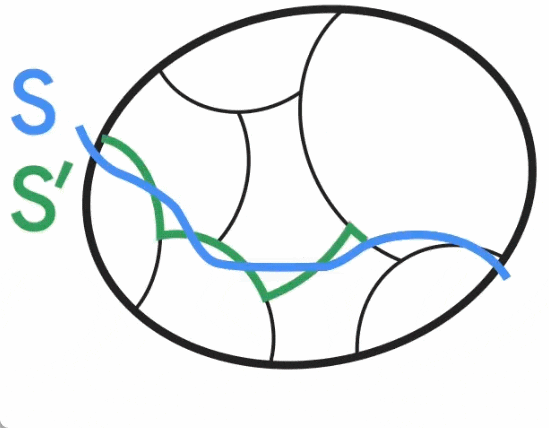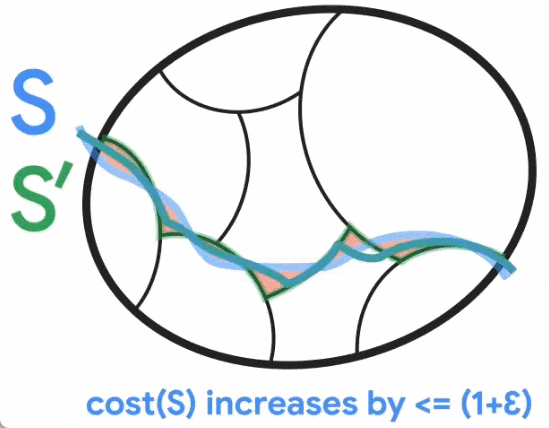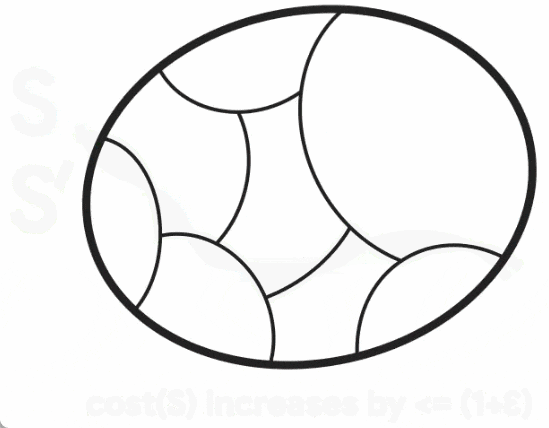 
참고 링크: https://research.google/blog/solving-the-minimum-cut-problem-for-undirected-graphs/위 내용은 무방향 그래프의 최소절단 문제에 새로운 돌파구를 마련해 구글 리서치가 SODA 2024 최우수 논문상을 수상했습니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
![[웹 프런트엔드] Node.js 빠른 시작](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
