테렌스 타오 등 많은 수학자로부터 극찬을 받아온 이 공식 수학 도구인 린 코파일럿(Lean Copilot)이 또 진화했다고요?
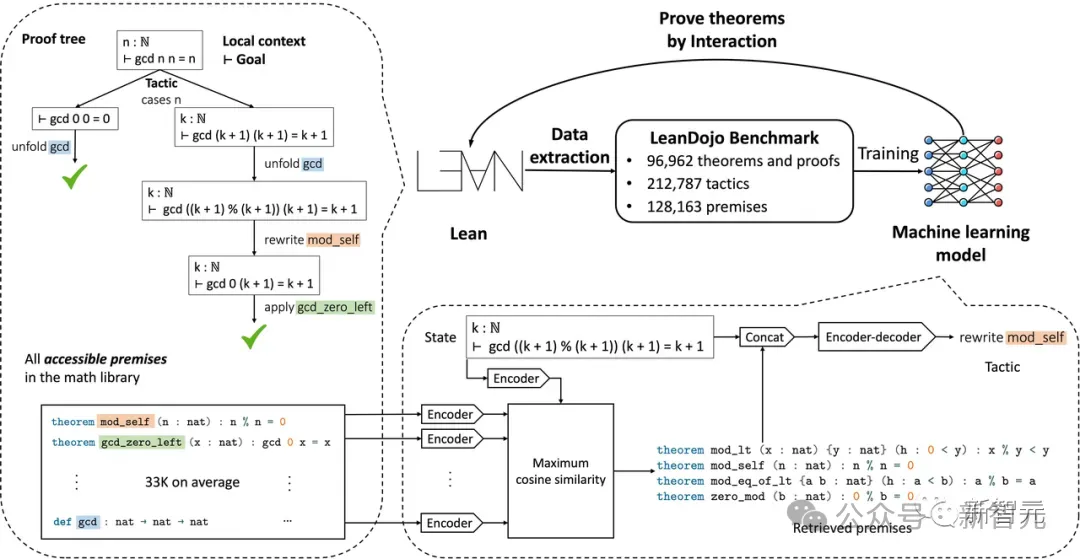
방금 Caltech 교수인 Anima Anandkumar는 팀이 Lean Copilot 논문의 확장 버전을 출시하고 코드 기반을 업데이트했다고 발표했습니다.
Pictures
문서 주소: https://arxiv.org/pdf/2404.12534.pdf
최신 실험에 따르면 이 Copilot 도구는 수학적 증명 단계의 80% 이상을 자동화할 수 있습니다! 이 기록은 이전 베이스라인 이솝보다 2.3배 향상된 기록이다.
그리고 이전과 마찬가지로 MIT 라이선스에 따른 오픈 소스입니다.
Pictures
그는 중국 소년 Song Peiyang입니다. 그는 UCSB의 명예 CS 학부생이자 California Institute of Technology의 컴퓨팅 + 수리 과학(CMS) 부서의 SURF 연구원입니다.
네티즌들은 다음과 같이 외쳤습니다. 그렇다면 Tao Zhexuan의 수학적 연구는 이제 제자리에서 5배 가속화될 수 있습니까?
Pictures
팀은 100% 정확한 공식 수학 증명을 작성하기 위해 인간과 LLM 간의 협력을 시작하기를 희망하면서 이 Lean Copilot 도구를 출시했습니다.
Lean에서 LLM 추론을 실행하는 핵심 기술 과제를 해결합니다.
이 도구를 통해 LLM은 Lean에서 증명 전략을 제안하여 인간이 원활하게 개입하고 수정할 수 있도록 할 수 있습니다.
Pictures
이 프로젝트는 자동화된 정리 증명이 오늘날에도 여전히 어려운 과제이기 때문에 개발되었습니다.
우리는 LLM이 수학과 추론 작업을 수행할 때 종종 실수와 환각을 일으키고 매우 신뢰할 수 없다는 것을 알고 있습니다.
Pictures
그래서 지금까지 수학적 증명은 대부분 수동으로 도출되었으며 신중한 검증이 필요합니다.
Lean과 같은 정리 증명 도구는 증명 과정의 모든 단계를 공식화할 수 있지만 인간이 Lean을 작성하는 것은 정말 힘든 일입니다.
이 경우 Lean Copilot의 탄생은 큰 의미를 갖습니다.
LLM은 정리를 증명하는 데 인간을 돕는 도구로 사용될 수 있습니다. 이 주장은 Tao Zhexuan에 의해 여러 번 확인되었습니다.
그는 자신의 블로그에서 26년 안에 AI가 검색 및 기호 수학 도구와 결합되어 수학 연구에서 신뢰할 수 있는 공동 저자가 될 것이라고 예측했습니다.
그 직후 그의 관점을 뒷받침하는 연구가 비가 내린 뒤 버섯처럼 솟아올랐다.
Pictures
9월, Microsoft Research Asia, Peking University, Beihang University 및 기타 기관의 연구원들이 97차례의 "소크라테스식" 엄격한 추론을 통해 GPT-4를 성공적으로 만들었다는 결론에 도달했습니다. "P≠NP"로 이 밀레니엄 문제를 해결했습니다.
Pictures
97차 대화에서 GPT-4는 철저한 방법 없이는 예시를 해결할 수 없다고 결론을 내렸고, 결론은 P≠NP
지난 10월, Tao Zhexuan임을 증명했습니다. GPT-4와 Copilot의 도움으로 그의 논문에서 숨겨진 버그를 직접 발견했습니다.
Lean4를 사용하여 6페이지의 인수를 공식화하는 과정에서 그는
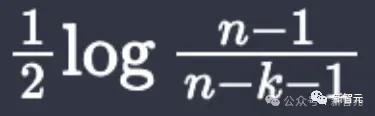picture
표현식이 n=3,k=2일 때 실제로 발산한다는 사실을 발견했습니다.
이 보기 힘든 버그는 Lean4 덕분에 제때에 잡혔습니다. 그 이유는 Lean이 그에게 0
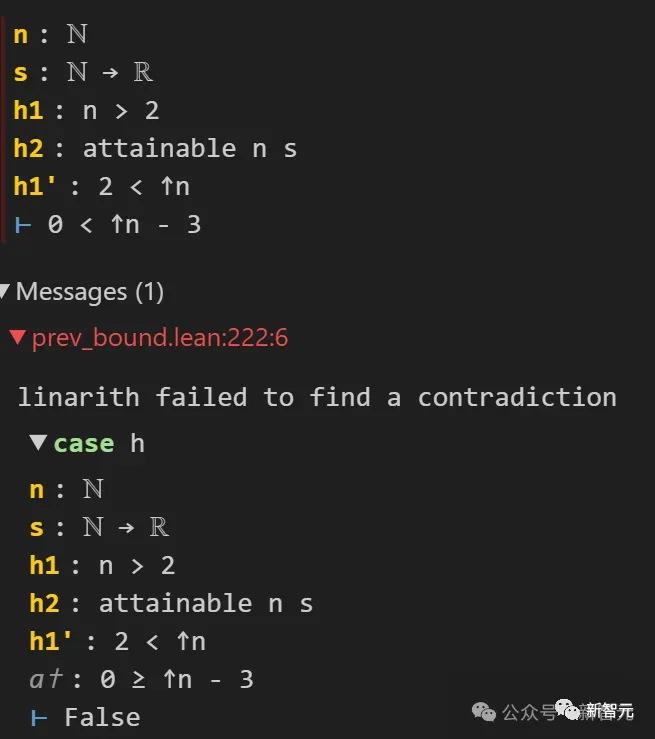Pictures
이 발견은 Tao Zhexuan의 학생들에게 직접적인 충격을주었습니다.
Pictures
작년 말, Tao Zhexuan은 AI 도구를 직접 성공적으로 사용하여 다항식 Freiman-Ruzsa 추측 증명 프로세스를 공식화하는 작업을 완료했습니다.
Picture
마지막으로 종속성 그래프는 완전히 녹색으로 덮여 있으며 Lean 컴파일러는 이 추측이 표준 공리를 완전히 따른다고 보고합니다.
Pictures
이 과정에서 모든 일선 수학 연구자들은 AI가 수학 연구의 전복적인 힘에 미치는 직접적인 영향을 처음으로 느꼈습니다.
그리고 오늘날 Lean Copilot의 이 연구는 Lean을 직접적으로 더욱 강력하게 만들었습니다.
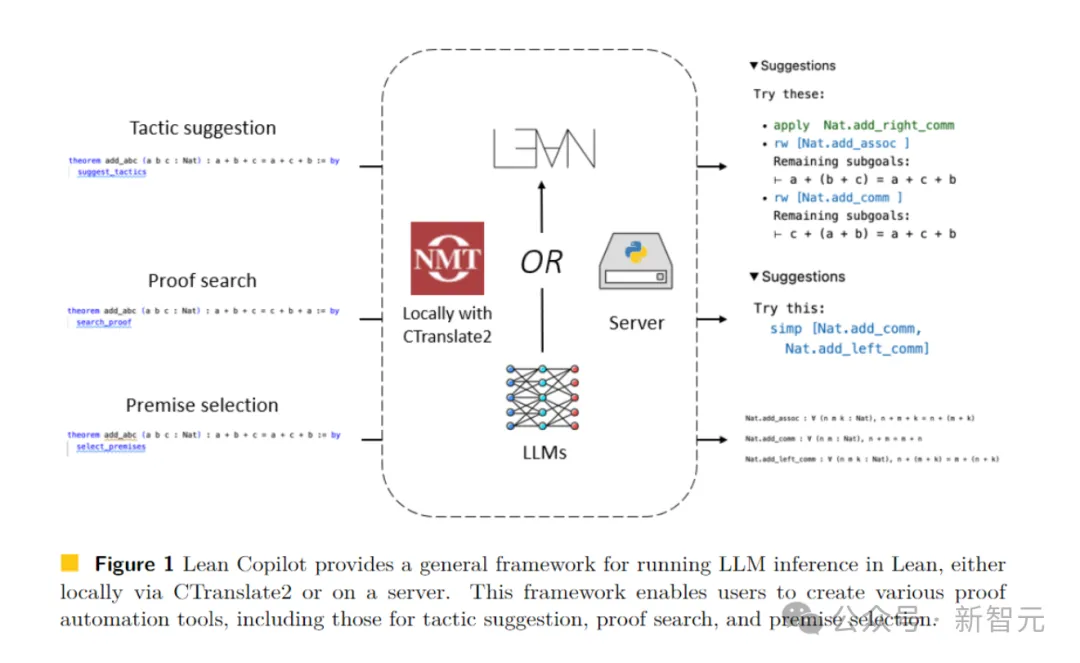
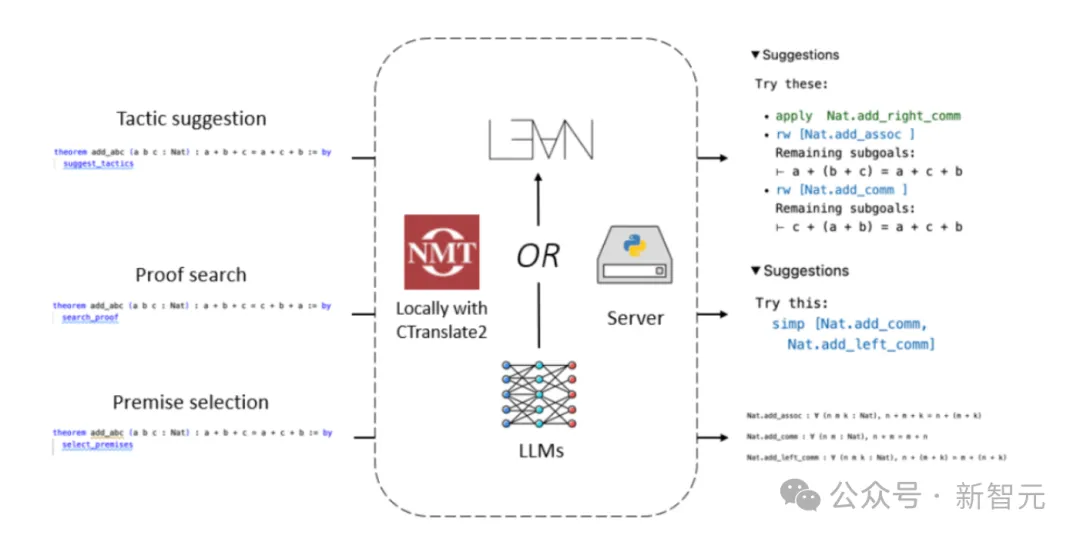
이 문서에서 팀은 증명 단계 제안(전략 제안), 중간 증명 목표 완료(증명 검색), LLM을 사용하여 관련 건물 선택(전제 선택)을 위한 Lean Copilot 기반 도구를 구축했습니다.
실험 결과는 기존 Lean의 규칙 기반 증명 자동화와 비교하여 Lean Copilot이 인간의 자동화 정리 증명을 돕는 데 효과적이라는 것을 충분히 보여줍니다.
Lean Copilot은 CTranslate 2를 통해 로컬로 또는 서버에서 LLM 추론을 실행할 수 있는 일반 프레임워크를 제공합니다.
이 프레임워크를 통해 사용자는 다양한 자동화된 교정 도구를 만들 수 있습니다.
Pictures
Lean은 수학자 사이에서 매우 인기 있는 증명 보조 도구입니다. 아래 그림에서 볼 수 있듯이 Lean의 증명은 전술이라는 일련의 증명 단계로 구성됩니다.
Pictures
전체 정리를 초기 목표로 시작하여 모든 목표가 해결될 때까지 현재 목표를 더 간단한 하위 목표로 반복적으로 변환하는 전략입니다.
사용자는 VSCode로 구동되는 IDE에서 대화형으로 전략을 작성하고 목표는 오른쪽의 정보 보기 패널에 표시됩니다.
Lean Copilot을 사용하여 팀은 LLM을 사용하여 전략 제안을 생성하는 도구인 presents_tropics를 구축했습니다.
그리고 그것 자체도 전략입니다.
을 적용하면 현재 대상을 LLM에 입력하고 생성된 정책 후보 목록을 LLM에서 가져옵니다.
각 옵션을 살펴보고 1) 오류가 발생했는지, 2) 아무 문제가 없지만 증명을 완료하지 못했는지, 3) 증명을 성공적으로 완료했는지 확인합니다.
1)인 경우 해당 전략이 삭제됩니다.
Pictures
오른쪽 보기 패널에는 오류가 없는 전략만 표시됩니다.
그 중 증명을 성공적으로 완료한 전략은 녹색(범주 3)으로 표시되고, 오류 없이 증명 목표를 변경했지만 증명을 완료하지 못한 전략은 파란색(범주 2)으로 표시됩니다.
주의! 나열된 모든 전략이 범주 2에 속하면 이 정보는 사용자에게 매우 중요할 수 있습니다.
이 경우 남은 목표에 대한 정보는 사용자가 다음 중간 증명 단계로 전략을 선택하는 데 직접적인 도움이 될 수 있습니다.
사용자는 제안을 본 후 이를 수락할지 아니면 새로운 전략을 개발하기 위한 영감의 원천으로 사용할지 선택할 수 있습니다.
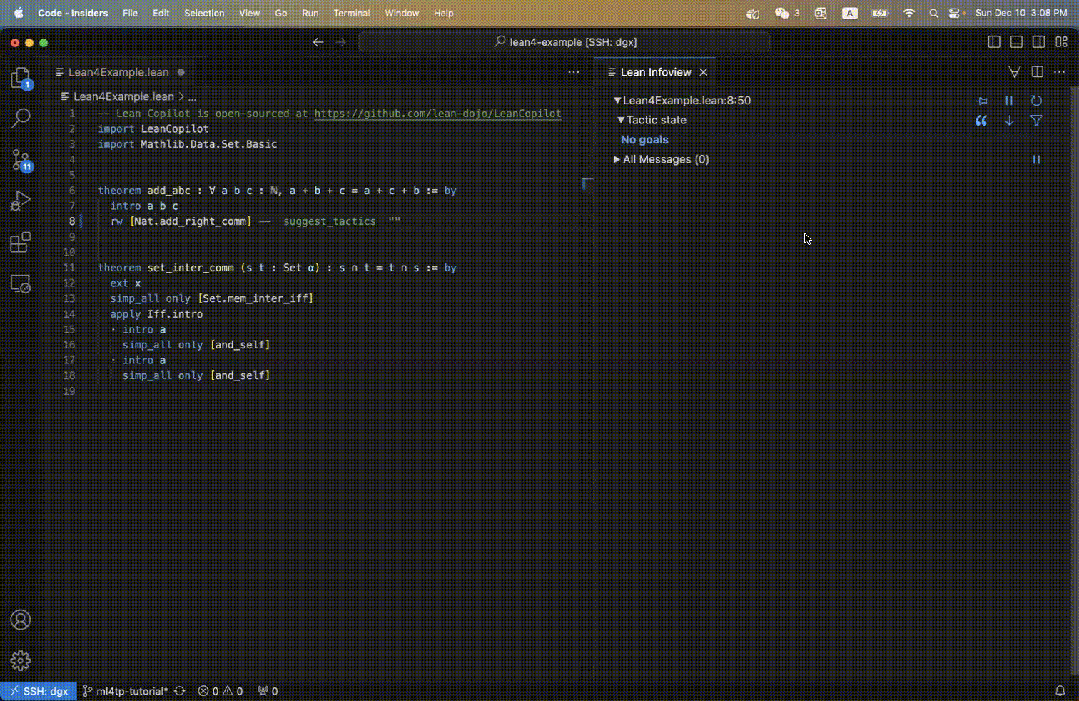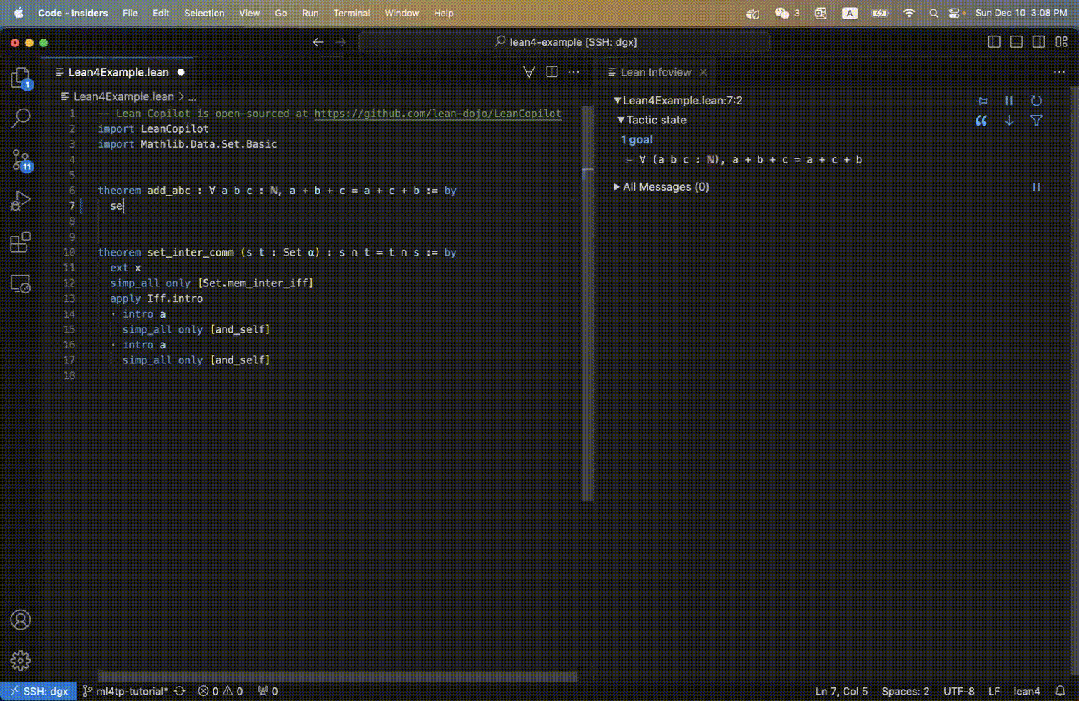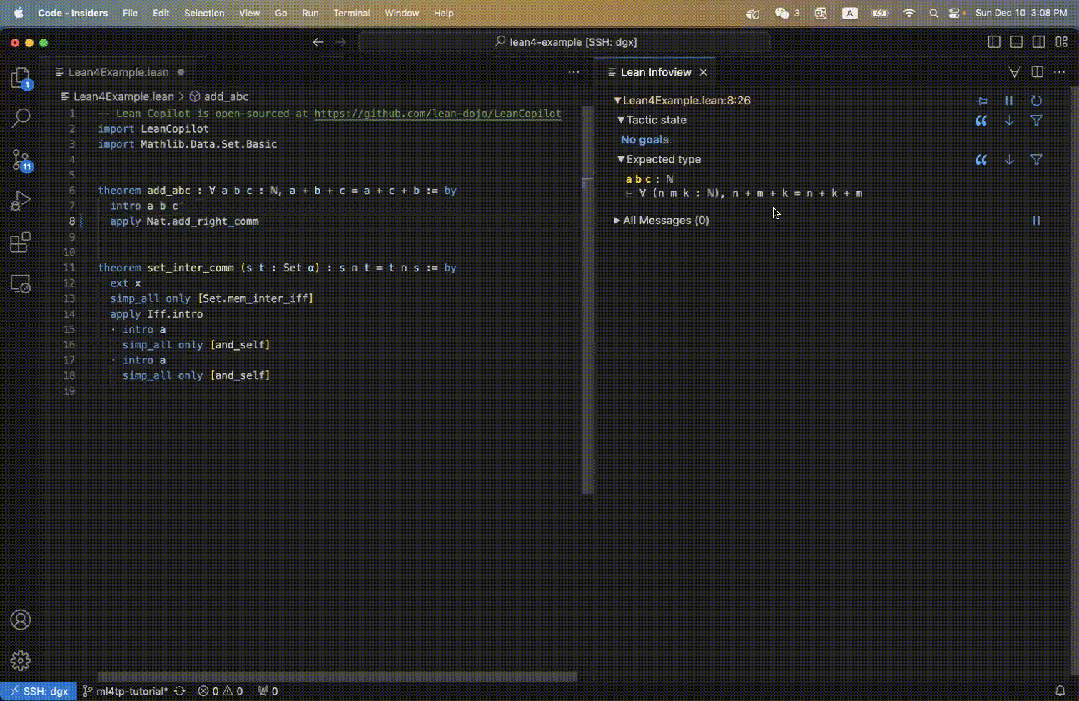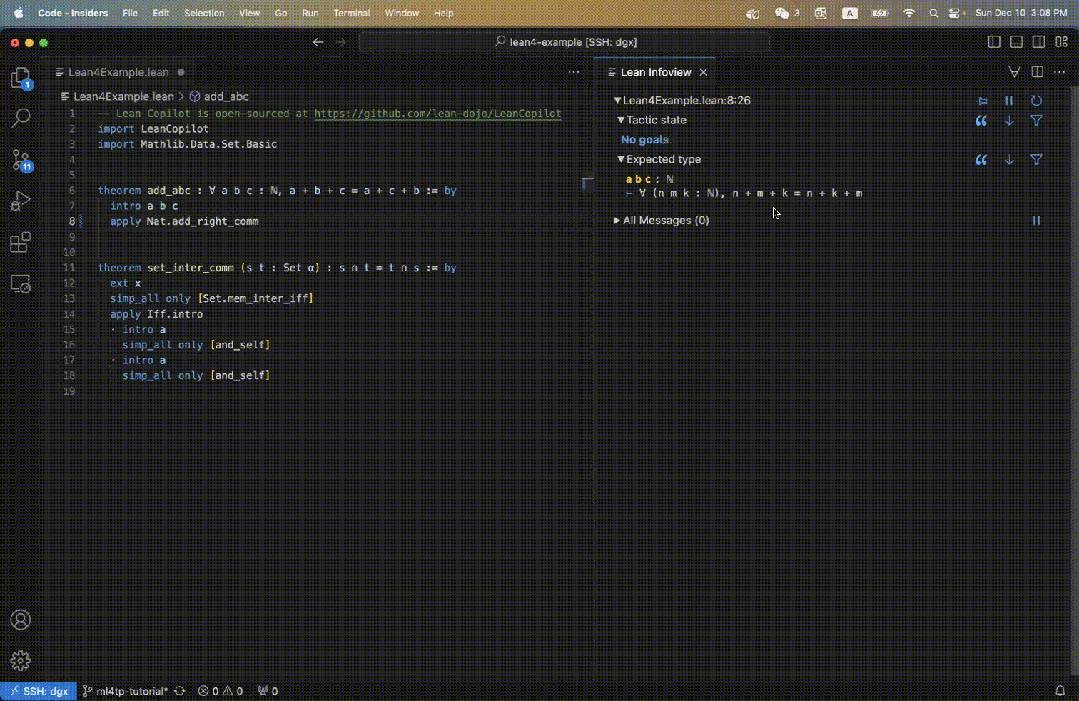
예를 들어 Lean 코드에서 add_abc 정리를 정의하고 초기 목표는 그림 3의 오른쪽에 표시됩니다.
Pictures
suggest_tropics에 들어가면 오른쪽에 전략 제안이 표시됩니다.
첫 번째 전략은 녹색으로 표시되어 증명이 성공적으로 완료되었음을 나타냅니다.
다음 세 가지 제안은 모두 파란색입니다. 이는 증명을 직접 완료할 수는 없지만 오류로 이어지지 않음을 나타냅니다.
따라서 유효한 중간 증명 단계가 될 가능성이 높습니다!
동시에 남은 하위 목표도 표시됩니다.
하나 이상의 전략 제안이 입증될 수 있으므로 전술 상태 필드에 목표 없음이 표시됩니다.
Pictures
게다가 인간이나 기계 모두 지속적으로 올바른 전략을 생성할 수 없기 때문에 프로세스는 역추적하여 다양한 대안, 즉 증거 검색을 탐색해야 합니다.
위에서 언급한 Suggest_tropics의 경우 현재 단계의 전략만 생성할 수 있으며 다중 전략 증명을 검색하는 기능은 없습니다.
이를 위해 팀에서는 이를 규칙 기반 증명 검색 도구인 aesop과 결합하여 LLM 기반 증명 검색 도구를 구축했습니다.
Aesop은 Lean 전략으로 최선의 검색을 구현하고 사용자가 검색 트리 확장 방법을 구성할 수 있도록 합니다.
Pictures
검색 트리는 노드인 대상으로 구성됩니다.
처음에는 원래 대상만 루트 노드로 갖습니다. 각 단계에서 aesop은 가장 유망한 확장되지 않은 노드를 선택하고 정책을 적용하여 확장한 후 결과 노드를 하위 노드로 추가합니다.
사진
그리고 이솝이 근본 원인부터 쉽게 해결할 수 있는 목표까지의 경로를 찾아낸다면, 이는 검색이 성공했음을 증명합니다!
따라서 이솝의 성능은 사용자가 효과적인 규칙 세트를 구성하는지 여부에 따라 결정적으로 달라집니다.
이솝은 유연성이 부족하다는 것을 보여줍니다. 따라서 Search_proof는 각 단계에서 presents_tropics에 의해 생성된 대상 관련 정책을 보다 유연하게 만들어 aesop의 규칙 세트를 강화합니다.
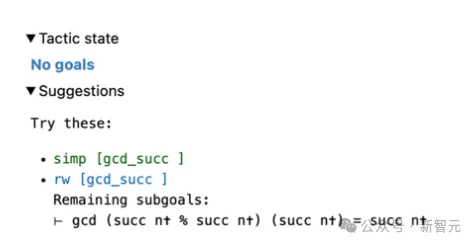
그림 3의 원래 목표의 경우 사용자는 search_prrof를 입력하고 목표를 해결할 수 있는 완전한 증거를 찾으면 정보 보기에 표시됩니다(그림 5 오른쪽).
성공의 증거가 발견되었으므로 남은 Tactic 상태는 No goal임을 알 수 있습니다.
Pictures
또한 정리 증명에서 또 다른 도전적이고 중요한 작업은 증명을 축소하거나 완성하는 관련 전제를 찾는 것입니다.
린에는 소스 코드 라이브러리와 표준 라이브러리의 수많은 전제 조건 외에도 대규모 수학 라이브러리(Mathlib)도 있습니다.
그러나 모든 도서관에서 후보 건물을 검색하는 것은 매우 어렵고 시간이 많이 걸립니다.
너무 많은 사람들이 Lean이나 다른 증명 보조원으로부터 도움을 받거나 이 프로세스를 자동화하려고 노력하고 있습니다.
Pictures
Lean에서 가장 발전된 전제 선택 방법은 Lean에서 직접 구현한 Random Forest(랜덤 포레스트) 기반의 프레임워크입니다.
그러나 전제 선택 작업은 검색 강화 LLM에 매우 적합합니다. 여기서 검색 행렬(전제 임베딩)은 증명 대상과 후보 전제 간의 상관 관계를 추정하기 위해 대규모 모델 훈련 중에 훈련됩니다.
추론 시 증명 목표가 주어지면 먼저 목표를 벡터로 인코딩한 다음 전제 임베딩과 목표 벡터 간의 행렬-벡터 곱셈을 수행합니다.
그런 다음 상위 k개 전제를 선택하려면(여기서 k는 사용자가 반환하려는 전제 수를 결정하는 하이퍼 매개변수일 수 있음) 가장 높은 점수를 가진 k개 전제를 반환하면 됩니다.
Lean에서 추론 작업을 수행하려면 Lean Copilot에서 제공하는 빠른 추론 외에도 효율적인 행렬 곱셈 라이브러리와 C++ numpy 행렬 판독기가 필요합니다.
연구원들은 CTranslate2의 행렬 곱셈 기능과 Libnpy의 C++ 고속 numpy 파일 판독기를 사용했습니다.
그들은 FFI 메커니즘을 통해 이 숫자를 Lean에 다시 연결합니다.
따라서 전제 임베딩을 미리 계산할 수 있고 위에 소개된 라이브러리를 사용하여 C++에서 모든 후속 작업을 빠르게 수행할 수 있으므로 전제 선택 전략은 매우 효율적으로 실행될 수 있습니다.
연구원은 반품 전제를 얻은 후 유용한 정보를 추가로 주석 처리했습니다.
여기서 모든 건물은 현재 환경에서 직접 사용할 수 있는 건물(범위 내 건물)과 현재 환경에서 직접 사용할 수 없는 건물(범위 밖 건물)의 두 가지 범주로 구분됩니다.
이는 필수 패키지를 가져왔는지 여부에 따라 다릅니다.
전제에 필요한 패키지를 이미 가져온 경우 전제를 쉽게 사용할 수 있습니다. 아래 그림 6은 주석이 달린 범위 전제를 보여줍니다.
그림 7은 주석이 달린 범위 밖 전제를 보여줍니다.
다음은 그림 3의 정리 add_abc의 경우 증명에 select_premise를 직접 입력할 수 있는 "전제 선택"을 사용한 예입니다(그림 8 왼쪽).
그러면 관련 전제 조건 목록이 정보 보기에 표시됩니다(그림 8, 오른쪽).
이 간단한 정리의 경우 선택한 전제가 모두 자연수 및 덧셈 규칙과 관련되어 있기 때문에 실제로 관련성이 있음을 분명히 볼 수 있습니다.
이 경우 선택한 4개 건물은 모두 현재 범위에 속하며 이는 해당 모듈을 이미 가져왔음을 의미합니다.
위는 Lean Copilot을 통해 연구원들이 구축한 세 가지 실용적인 증명 자동화 도구로, 전략 제안, 검색 증명 및 전제 선택에 사용됩니다.
Lean Copilot 프레임워크를 통해 연구자들은 ITP(Lean Interactive Theorem Proving)에서 인간-기계 협업이 유익하다는 가설을 경험적으로 제시했습니다.
Lean의 정리 증명 프로세스로 인해 주로 전략 증명에 중점을 둡니다.
따라서 저자는 특정 실험에서 "전략 제안"과 "증명 검색"을 위한 증명 자동화 도구를 주로 평가했습니다.
요약하자면, 이솝은 현재 증명 검색을 위한 가장 발전된 규칙 기반 증명 자동화 도구입니다.
연구원들은 두 가지 경우에 이솝과 비교하여 LLM 기반 검색 증명의 효율성을 확인했습니다.
(1) 자율 증명(LLM은 독립적으로 완료됨)
(2) Assistance Humans done theorem Proving (인간과 AI 협업)
또한 연구원들은 단일 전략 제안 외에도 검색 증명의 장점을 입증하기 위해 검색 증명과 전략 제안을 비교했습니다.
소프트웨어 프로그래밍에서 인간이 Copilot을 사용하는 패러다임과 유사하게 Lean Copilot이 ITP 과정에서 어떻게 인간을 효과적으로 도울 수 있는지 연구하세요.
즉, 목표에 직면하면 먼저 Copilot에 전화하여 문제를 직접 해결할 수 있는지 확인합니다.
그렇지 않다면 목표를 더욱 단순화하고 Copilot을 다시 시도합니다. 그런 다음 Copilot이 나머지 목표를 성공적으로 해결할 때까지 위 프로세스를 반복합니다.
연구원들은 이 반복적인 협업 예시를 사용하여 각 증명 자동화 도구가 얼마나 많은 인력을 자동화할 수 있는지 확인했습니다.
구체적인 결과는 아래 표 1과 같습니다.
증명 검색(search_proof)은 정리의 64%(50개 중 32개)를 자동으로 증명할 수 있으며, 이는 이솝 및 전략 제안(suggest_tropics)보다 훨씬 높은 수치입니다.
인간을 돕기 위해 사용될 때 증명 검색에는 평균 1.02개의 수동 입력 전략만 필요하며 이는 이솝(3.62) 및 전략 제안(2.72)보다 낫습니다.
그림
마지막으로 테스트된 각 정리에 대해 저자는 세 가지 도구 각각으로 자동화할 수 있는 증명 단계의 비율을 계산했습니다.
그 결과 증명 검색은 정리의 증명 단계 중 약 81.2%를 자동으로 완료할 수 있는 것으로 나타났으며 이는 전략 제안(48.6%) 및 이솝(35.2%)보다 훨씬 높습니다.
요약하자면, 증명검색의 성능은 정책 제안보다 1.67배, 규칙 기반 기준선 이솝보다 2.31배 더 좋습니다.
Lean Copilot의 전술적 제안, 증명 검색 및 전제 선택 이 세 가지 작업은 본질적으로 다르게 보일 수 있지만 사용자 경험에 대한 요구 사항은 유사합니다.
모두 린에서 실행되는 동안 충분히 빠르게 응답을 생성하고 적당한 컴퓨팅 요구 사항을 충족해야 합니다.
사용자가 이러한 요구 사항을 갖는 이유는 Lean 자체가 대부분의 경우 환경 피드백(남은 대상, 오류 메시지, 유형 정보 등)을 매우 빠르게 제공할 수 있기 때문입니다.
이 속도는 정리 증명의 본질과 일치합니다. 이를 위해서는 일관된 추론이 필요합니다.
Lean Copilot이 사용자에게 오랜 시간을 기다려야 한다면 인간과 AI 간의 협업이 작동하기 어려울 것입니다.
마찬가지로 우리도 낮은 컴퓨팅 요구 사항을 충족하고 싶습니다. Lean 자체의 정리 증명은 GPU가 필요하지 않으며 사용자의 로컬 노트북에서 실행될 수 있기 때문입니다.
따라서 Lean 사용자가 대부분의 하드웨어(GPU가 없는 노트북 포함)에서 효율적으로 실행할 수 있는 것은 매우 중요합니다.
사용자가 교정을 작성할 때 CUDA 지원 GPU에 액세스하지 못할 수도 있기 때문입니다.
빠른 추론과 낮은 계산 요구 사항이 충족되어야 하고 널리 사용되고 효율적인 모든 딥 러닝 프레임워크가 Python에 있기 때문에 팀이 생각한 자연스러운 솔루션은 모델을 Python(로컬 또는 원격)에서 호스팅하는 것이었습니다. 그런 다음 Lean에서 모델에 요청합니다.
그러나 이 접근 방식은 프로세스 간 통신의 오버헤드가 발생하고 사용자가 추가 설정 단계를 수행해야 하며 Lean의 기존 워크플로에는 적합하지 않습니다.
이러한 문제를 극복하기 위해 Lean Copilot은 FFI(외부 기능 인터페이스)를 통해 기본적으로 Lean에서 LLM을 실행합니다.
FFI는 한 언어로 작성된 프로그램이 다른 언어로 서브루틴을 호출할 수 있도록 하는 메커니즘입니다.
Lean 부분은 C++로 구현되었으며 C++와 효율적으로 상호 운용할 수 있습니다.
프로그래머는 Lean에서 함수를 선언할 수 있지만 함수 본문은 C++로 구현할 수 있습니다. 구현은 공유 라이브러리로 컴파일되고 Lean에 동적으로 연결됩니다.
기본적으로 LeanDojo 사전 훈련된 Repver 모델을 사용합니다. 이는 입력 문자열을 출력 문자열로 매핑하는 인코더-디코더 변환기 BVT5를 기반으로 합니다.
Lean Copilot은 FFI를 통해 Lean에서 호출할 수 있는 문자열에서 작동하는 C++ 함수로 모델을 래핑하여 Lean에서 실행할 수 있도록 합니다.
Pictures
최신 논문의 3인 팀은 6월 23일 오픈 소스 플랫폼 LeanDojo의 저자이기도 합니다.
Pictures
문서 주소: https://arxiv.org/pdf/2306.15626.pdf
사진
노래 Peiyang은 Richert Wang과 Phill Conrad의 멘토링을 받는 UC Santa Barbara의 CCS(College of Creative Studies)에서 컴퓨터 공학을 전공하는 우등 학부생입니다.
동시에 그는 Anima Anandkumar 교수와 Kaiyu Yang 박사가 공동 지도하는 Caltech 컴퓨터 및 수리과학과(CMS)의 SURF 연구원이기도 합니다.
Pictures
또한 그는 UC Berkeley Architecture Lab의 연구원으로 Tim Sherwood 및 Dr. Jeremy Lau(Google)와 함께 일하고 있습니다.
그의 연구 관심 분야는 자연어 처리(NLP), 컴퓨터 비전(CV) 등의 응용 분야와 시스템 및 프로그래밍 언어(PL) 등의 기본 이론을 포함하는 기계 학습(ML)입니다.
송페이양의 최근 연구는 크게 두 가지 방향으로 진행됩니다.
하나는 대형 모델과 대화형 정리 증명기(ITP)를 결합한 신경 기호 추론 및 인공 지능 수학(AI4Math)입니다.
다른 하나는 시간적 논리를 기반으로 한 에너지 효율적인 머신러닝입니다.
Picture
Kaiyu Yang은 Caltech 컴퓨터 + 수학 과학(CMS) 학과의 박사후 연구원으로 Anima Anandkumar의 멘토를 받았습니다.
그는 프린스턴 대학에서 박사학위를 받았으며 그의 지도교수는 Jia Deng이었고 Olga Russakovsky 및 Chen Danqi와도 함께 일했습니다.
그의 연구는 기계 학습이 상징적 추론을 수행할 수 있도록 하는 것을 목표로 하는 신경기호 인공 지능에 중점을 두고 있으며 이를 두 가지 방향을 통해 달성하고자 합니다.
(1) 형식 논리와 같은 상징적 추론 작업에 기계 학습을 적용합니다. 또는 자연어로 증명하는 수학적 추론 및 정리
(2) 기계 학습 모델에 기호 구성 요소를 도입하여 보다 해석 가능하고 검증 가능하며 데이터 효율성을 높입니다.
현재는 수학을 이해하고 추론할 수 있는 인공지능을 연구하고 있습니다. 수학적 추론은 인간 지능의 중요한 이정표이며 편미분 방정식 풀기 및 공식 검증과 같은 과학 및 공학의 많은 중요한 문제를 변화시킬 수 있는 잠재력을 가지고 있습니다.
Anima Anandkumar는 현재 Caltech의 계산 및 수학 과학 교수입니다.
Pictures
그녀의 연구 관심 분야는 주로 대규모 기계 학습, 비볼록 최적화 및 고차원 통계 분야에 중점을 두고 있습니다.
특히, 머신러닝을 위한 텐서 알고리즘 개발과 분석을 주도해 왔습니다.
텐서 분해 방식은 병렬성과 확장성이 매우 높아 대용량 데이터에 적용할 수 있습니다. 이는 최적의 솔루션으로의 수렴을 보장하고 많은 확률 모델(예: Markov 모델)에 대해 일관된 추정 결과를 출력할 수 있습니다.
https://www.php.cn/link/1dd5a4016c624ef51f0542d4ae60e281
위 내용은 Caltech Chinese는 AI를 사용하여 수학적 증명을 뒤집습니다! 충격적인 Tao Zhexuan의 속도 5배 향상, 수학 단계의 80%가 완전 자동화됨의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
![[웹 프런트엔드] Node.js 빠른 시작](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
