Transformer가 Kansformer가 되고 싶나요? 도전자 KAN을 안내하는 데 수십 년을 보낸 MLP

MLP(Multilayer Perceptron)가 수십년 동안 사용되어왔는데 정말 다른 선택이 없나요?

완전 연결된 피드포워드 신경망으로도 알려진 다층 퍼셉트론(MLP)은 오늘날 딥 러닝 모델의 기본 구성 요소입니다.

MLP는 기계 학습에서 비선형 함수를 근사화하는 기본 방법이므로 그 중요성은 아무리 강조해도 지나치지 않습니다.

그러나 MLP가 우리가 구축할 수 있는 최고의 비선형 회귀 분석기입니까? MLP는 널리 사용되지만 심각한 단점이 있습니다. 예를 들어 Transformer 모델에서 MLP는 거의 모든 비포함 매개변수를 사용하며 일반적으로 사후 처리 분석 도구가 없는 Attention 레이어에 비해 해석하기가 어렵습니다.

그렇다면 MLP의 대안이 있나요?

오늘은 칸이 등장했습니다.

이것은 Kolmogorov-Arnold 표현 정리에서 영감을 받은 네트워크입니다.

• 링크: https://arxiv.org/pdf/2404.19756

• Github: https://github.com/KindXiaoming/pykan

연구가 공개되자마자 파문을 일으켰습니다. 해외 소셜 플랫폼에서 많은 관심과 토론을 벌이고 있습니다.

일부 네티즌들은 콜모고로프가 루머하트, 힌턴, 윌리엄의 1986년 논문보다 훨씬 이른 1957년에 다층 신경망을 발견했지만 서방에서는 그를 무시했다고 말했습니다.

일부 네티즌들은 이 논문의 공개가 딥러닝의 종말이 왔다는 것을 의미한다고도 말했습니다.

일부 네티즌들은 이 연구가 트랜스포머 논문만큼 파괴적일지 궁금해했습니다.

그러나 일부 저자는 2018-19년에 개선된 콜모그로프-가보르 기법을 기반으로 동일한 작업을 수행했다고 말했습니다.

다음으로 이 논문의 내용을 살펴볼까요?

논문 개요

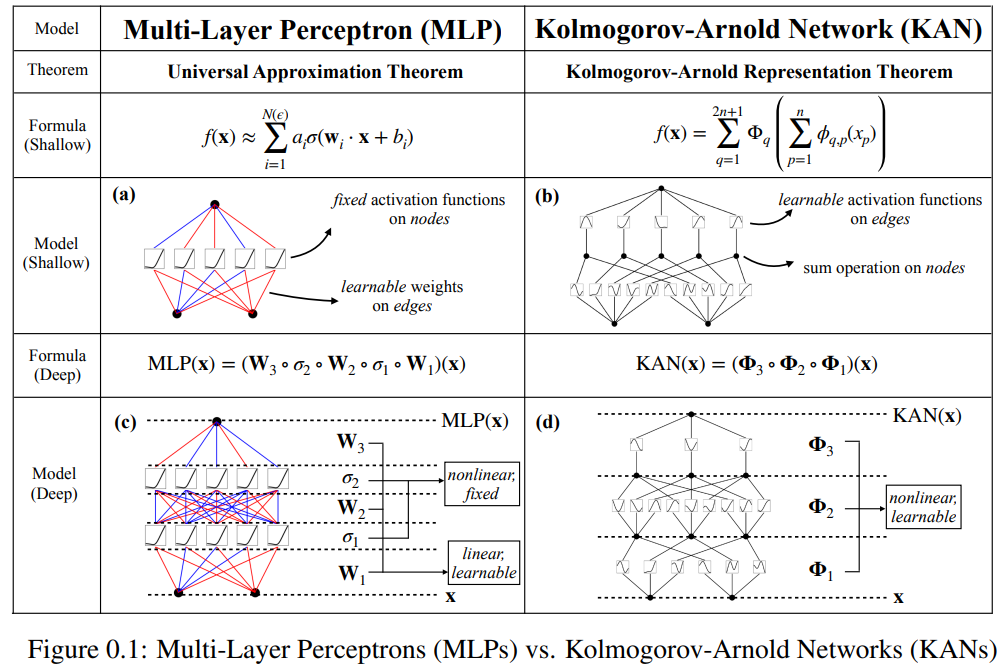
이 논문에서는 KAN(Kolmogorov-Arnold Networks)이라는 다층 퍼셉트론(MLP)에 대한 유망한 대안을 제안합니다. MLP의 디자인은 보편적 근사 정리에서 영감을 얻었으며, KAN의 디자인은 Kolmogorov-Arnold 표현 정리에서 영감을 받았습니다. MLP와 유사하게 KAN은 완전 연결 구조를 가지고 있습니다. MLP가 고정 활성화 함수를 노드(뉴런)에 배치하는 반면, KAN은 그림 0.1과 같이 에지(가중치)에 학습 가능한 활성화 함수를 배치합니다. 따라서 KAN에는 선형 가중치 행렬이 전혀 없습니다. 각 가중치 매개변수는 스플라인으로 매개변수화된 학습 가능한 1차원 함수로 대체됩니다. KAN의 노드는 비선형 변환을 적용하지 않고 들어오는 신호를 합산합니다.

어떤 사람들은 각 MLP의 가중치 매개변수가 KAN의 스플라인 함수가 되기 때문에 KAN의 비용이 너무 높다고 걱정할 수도 있습니다. 그러나 KAN은 MLP보다 훨씬 작은 계산 그래프를 허용합니다. 예를 들어 연구원들은 PED 솔루션을 시연했습니다. 폭이 10인 2층 KAN은 폭이 100인 4층 MLP보다 100배 더 정확합니다(MSE는 각각 10^-7과 10^-5입니다). 매개변수 효율성도 100배 향상되었습니다(매개변수 수는 각각 10^2 및 10^4).

Kolmogorov-Arnold 표현 정리를 사용하여 신경망을 구성할 가능성이 연구되었습니다. 그러나 대부분의 작업은 원래 깊이 2, 너비(2n + 1) 표현에 머물고 있으며 네트워크를 훈련하기 위해 더 현대적인 기술(예: 역전파)을 활용할 기회가 없습니다. 이 기사의 기여는 원래 Kolmogorov-Arnold 표현을 임의의 너비와 깊이로 일반화하여 오늘날의 딥 러닝 분야에서 활성화하는 동시에 수많은 경험적 실험을 사용하여 "AI + science"는 KAN의 정확성과 해석 가능성의 이점을 활용합니다.

KAN은 훌륭한 수학적 설명 기능을 갖추고 있지만 실제로는 스플라인과 MLP의 장점을 모두 활용하고 단점을 피한 것일 뿐입니다. 스플라인은 저차원 기능에서 매우 정확하고 로컬로 쉽게 조정할 수 있으며 다양한 해상도 간에 전환할 수 있습니다. 그러나 스플라인은 조합 구조를 활용할 수 없기 때문에 심각한 COD 문제가 발생합니다. 반면 MLP는 특징 학습 기능으로 인해 COD의 영향을 덜 받지만, 일변량 함수를 최적화할 수 없기 때문에 저차원 공간에서는 스플라인만큼 정확하지 않습니다.

함수를 정확하게 학습하려면 모델이 조합 구조(외부 자유도)를 학습할 뿐만 아니라 일변량 함수(내부 자유도)도 잘 근사화해야 합니다. KAN은 외부적으로는 MLP와 유사하고 내부적으로는 스플라인과 유사하기 때문에 이러한 모델입니다. 결과적으로 KAN은 기능을 학습할 수 있을 뿐만 아니라(MLP와의 외부 유사성 덕분에) 이러한 학습된 기능을 매우 높은 정확도로 최적화할 수 있습니다(스플라인과의 내부 유사성 덕분에).

예를 들어 고차원 함수의 경우:

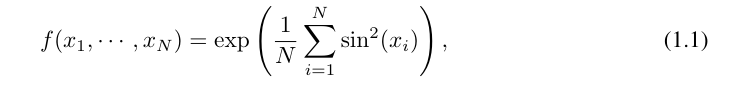
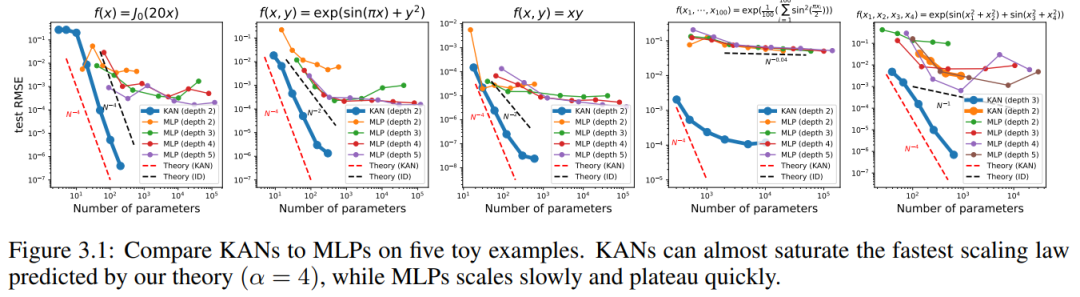
N이 크면 MLP가 일반화된 추가 구조를 학습할 수 있지만 스플라인은 COD로 인해 실패합니다. 지수 함수와 사인 함수를 근사화하는 ReLU 활성화 함수는 매우 비효율적입니다. 대조적으로, KAN은 조합 구조와 일변량 함수를 매우 잘 학습할 수 있으므로 MLP보다 큰 차이로 성능이 뛰어납니다(그림 3.1 참조).

이 논문에서 연구자들은 정확성과 해석 가능성 측면에서 KAN의 MLP의 상당한 개선을 반영하는 수많은 실험 값을 보여줍니다. 논문의 구조는 아래 그림 2.1에 나와 있습니다. 코드는 https://github.com/KindXiaoming/pykan에서 사용할 수 있으며 pip install pykan을 통해 설치할 수도 있습니다.

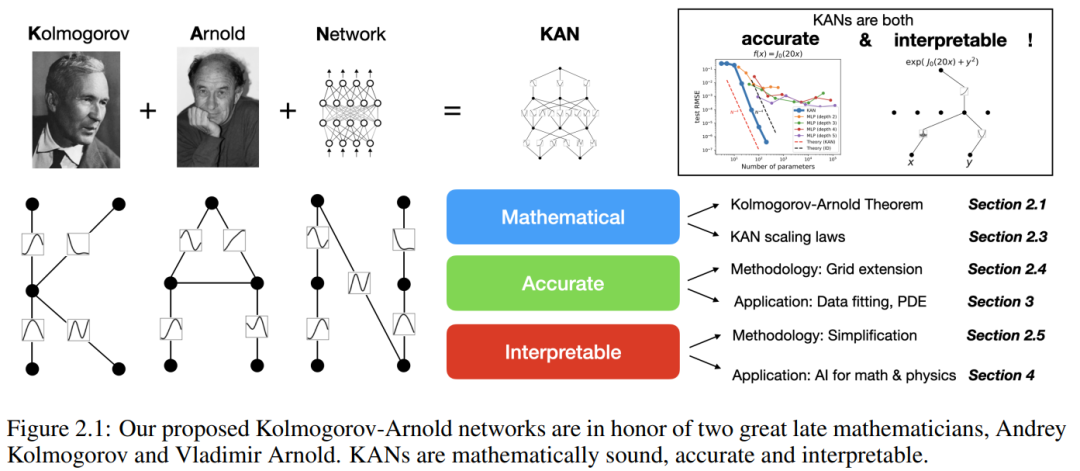
Kolmogorov-Arnold Network (KAN)

Kolmogorov-Arnold 표현 정리

Vladimir Arnold와 Andrey Kolmogorov는 f가 경계 영역에서 다변수 연속 함수인 경우 f는 다음과 같이 쓸 수 있음을 증명했습니다. 단일 변수 연속 함수와 이진 덧셈 연산의 유한한 조합입니다. 보다 구체적으로, 매끄러운 함수 f : [0, 1]^n → R의 경우 다음과 같이 표현될 수 있습니다:

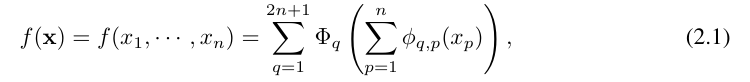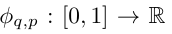where 및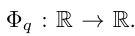

어떤 의미에서 그들은 유일한 진정한 다변량을 나타냅니다. 함수는 모두 덧셈입니다. 다른 함수는 단일 변수 함수 및 합계로 표현될 수 있습니다. 이것이 기계 학습에 좋은 소식이라고 생각할 수도 있습니다. 고차원 함수를 학습하는 것은 결국 다항식 양의 1차원 함수를 학습하는 것으로 귀결됩니다. 그러나 이러한 1차원 함수는 매끄럽지 않거나 심지어 프랙탈적일 수도 있으므로 실제로 학습되지 않을 수 있습니다. 따라서 Kolmogorov-Arnold 표현 정리는 본질적으로 기계 학습에서 사형 선고이며 이론적으로는 정확하지만 실제로는 쓸모가 없는 것으로 간주됩니다.

그러나 연구자들은 기계 학습에서 Kolmogorov-Arnold 정리의 실용성에 대해 더 낙관적입니다. 첫째, 2개의 비선형성 레이어와 은닉 레이어에 소수의 항(2n + 1)만 있는 원래 방정식을 고수할 필요가 없습니다. 연구원은 네트워크를 임의의 너비와 깊이로 일반화합니다. 둘째, 과학 및 일상 생활의 대부분의 기능은 일반적으로 매끄럽고 희박한 조합 구조를 가지고 있어 원활한 Kolmogorov-Arnold 표현을 용이하게 할 수 있습니다.

KAN 아키텍처

입력 및 출력 쌍 {x_i, y_i}로 구성된 지도 학습 작업이 있고 연구원이 모든 데이터 포인트에 대해 y_i ≒ f(x_i)가 되는 함수 f를 찾고자 한다고 가정합니다. 방정식 (2.1)은 적절한 단일 변수 함수 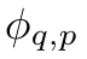및 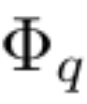를 찾을 수 있으면 작업이 완료됨을 의미합니다. 이는 연구자들이 방정식 (2.1)을 명시적으로 매개변수화하는 신경망을 설계하도록 영감을 줍니다. 학습할 모든 함수는 일변량 함수이므로 연구자는 로컬 B-스플라인 기반 함수의 학습 가능한 계수를 사용하여 각 1차원 함수를 B-스플라인 곡선으로 매개변수화합니다(그림 2.2의 오른쪽 참조). 이제 KAN의 프로토타입이 있는데, 그 계산 그래프는 방정식 (2.1)에 의해 완전히 지정되고 그림 0.1(b)(입력 차원 n = 2)에 설명되어 있으며 활성화 함수가 있는 2층 신경망처럼 보입니다. 노드 대신 가장자리(노드에서 간단한 합산이 수행됨), 중간 레이어 너비는 2n + 1입니다.

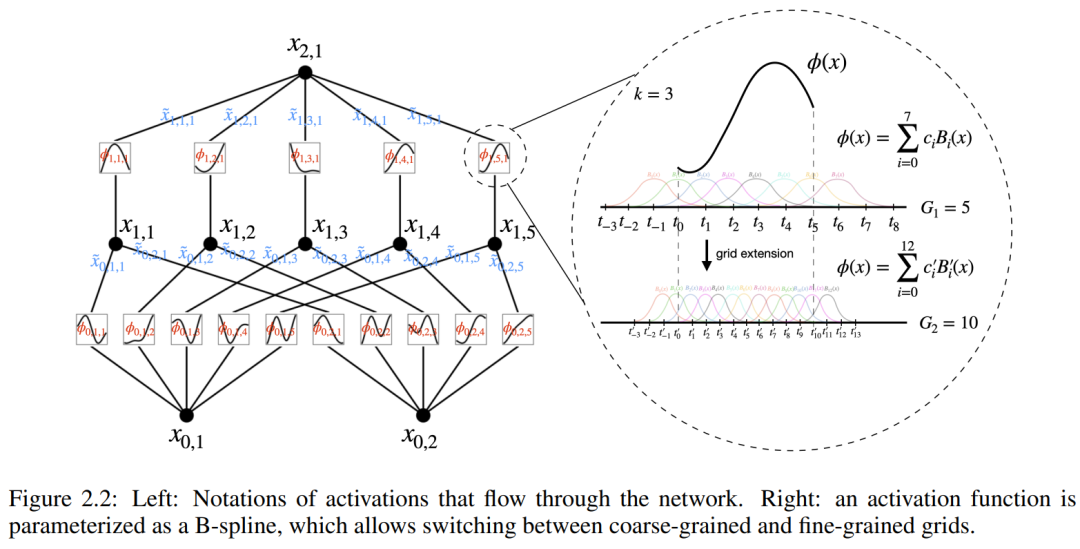
앞서 언급했듯이 실제로 이러한 네트워크는 임의의 정확도로 스무딩 스플라인을 사용하여 모든 기능을 근사화하기에는 너무 단순한 것으로 간주됩니다. 따라서 연구자들은 KAN을 더 넓고 더 깊은 네트워크로 일반화합니다. Kolmogorov-Arnold 표현은 2계층 KAN에 해당하므로 KAN을 더 깊게 만드는 방법이 명확하지 않습니다.

획기적인 점은 연구원들이 MLP와 KAN의 유사점을 발견했다는 것입니다. MLP에서는 선형 변환과 비선형성으로 구성된 계층이 정의되면 더 많은 계층을 쌓아 네트워크를 더 깊게 만들 수 있습니다. 깊은 KAN을 구축하려면 먼저 "KAN 레이어란 무엇입니까?"라고 대답해야 합니다. 연구원들은 n차원 입력과 n차원 출력을 갖는 KAN 레이어가 1차원 함수 행렬로 정의될 수 있음을 발견했습니다.

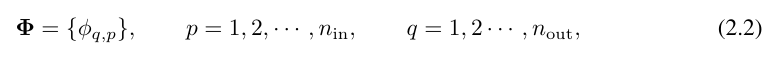
여기서 함수 에는 아래 설명과 같이 훈련 가능한 매개변수가 있습니다. Kolmogorov-Arnold 정리에서 내부 함수는 n_in = n 및 n_out = 2n+1인 KAN 계층을 형성하고, 외부 함수는 n_in = 2n + 1 및 n_out = 1인 KAN 계층을 형성합니다. 따라서 방정식 (2.1)의 Kolmogorov-Arnold 표현은 단순히 두 KAN 레이어의 조합입니다. 이제 더 깊은 Kolmogorov-Arnold 표현이 있다는 것은 더 많은 KAN 레이어를 쌓기만 하면 된다는 의미입니다!

더 깊은 이해를 위해서는 몇 가지 기호의 도입이 필요합니다. 구체적인 예와 직관적인 이해는 그림 2.2(왼쪽)를 참조하세요. KAN의 모양은 정수 배열로 표현됩니다.

여기서 n_i는 계산 그래프의 i번째 레이어에 있는 노드 수입니다. 여기서 (l, i)는 l번째 레이어의 i번째 뉴런을 나타내고, x_l,i는 (l, i) 뉴런의 활성화 값을 나타낸다. l번째 레이어와 l + 1번째 레이어 사이에는 n_l*n_l+1개의 활성화 함수가 있습니다. (l, j)와 (l + 1, i)를 연결하는 활성화 함수는

함수 ф_l로 표현됩니다. i,j의 활성화 전 값은 간단히 x_l,i로 표현됩니다. ф_l,i,j의 활성화 후 값은 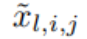ל,i,j (x_l,i)입니다. (l + 1, j)번째 뉴런의 활성화 값은 들어오는 모든 활성화 값의 합입니다.

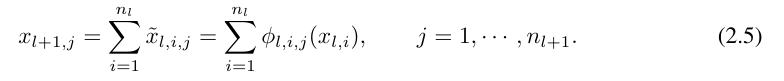
다음과 같이 행렬 형식으로 표현됩니다.

여기서, Φ_l은 에 해당하는 KAN 레이어입니다. l번째 레이어 함수 행렬. 일반적인 KAN 네트워크는 L 레이어의 조합입니다. 입력 벡터 x_0 ∈ R^n0이 주어지면 KAN의 출력은

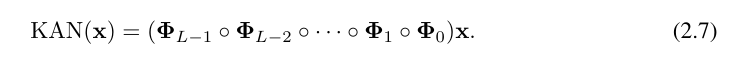
입니다. 위 방정식은 다음을 가정하여 방정식 (2.1)과 유사한 상황에서도 작성할 수 있습니다. 출력 차원 n_L = 1, f (x) DF KAN (x) 정의:

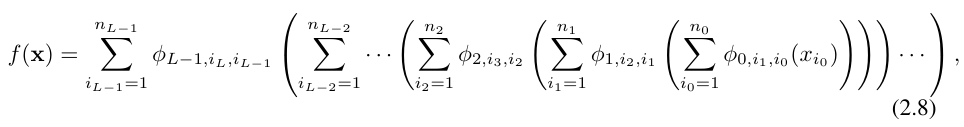
이렇게 글을 쓰다보니 꽤 지루하네요. 대조적으로, 연구원들의 KAN 레이어 추상화와 시각화는 더 간결하고 직관적입니다. 원래 Kolmogorov-Arnold 표현(2.1)은 [n, 2n + 1, 1] 모양의 2층 KAN에 해당합니다. 모든 작업은 미분 가능하므로 KAN은 역전파를 통해 훈련될 수 있습니다. 비교를 위해 MLP는 아핀 변환 W와 비선형 σ의 혼합으로 작성할 수 있습니다.

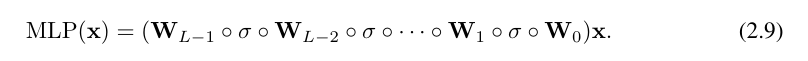
분명히 MLP는 선형 변환과 비선형성을 각각 W와 σ로 처리하는 반면 KAN은 이를 함께 Φ로 처리합니다. 그림 0.1 (c)와 (d)에서 연구원들은 3계층 MLP와 3계층 KAN을 보여줌으로써 둘 사이의 차이점을 보여줍니다.

KAN의 정확도

논문에서 저자는 다양한 작업(회귀 및 편미분 방정식 풀이)에서 함수를 표현하는 데 KAN이 MLP보다 더 효과적이라는 점도 입증했습니다. 그리고 그들은 또한 KAN이 치명적인 망각 없이 지속적인 학습에서 자연스럽게 기능할 수 있음을 보여줍니다.

toy Dataset

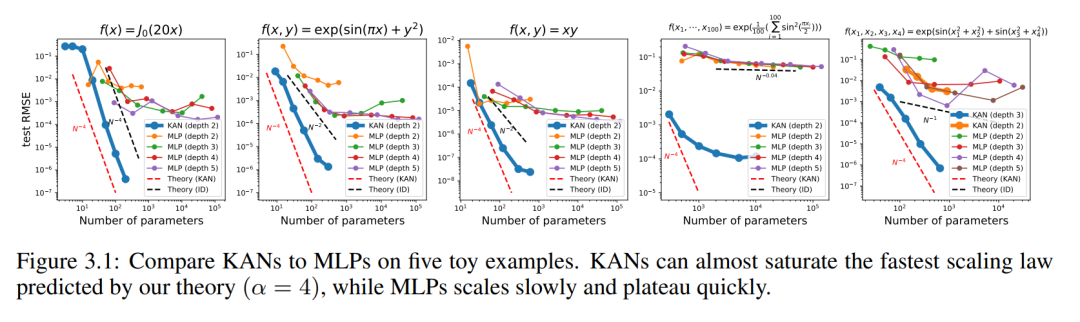
그림 3.1의 매개변수 수의 함수로 KAN 및 MLP의 테스트 RMSE를 플로팅하여 특히 고차원 예에서 KAN이 MLP보다 더 나은 스케일링 곡선을 가짐을 보여줍니다. 비교를 위해 저자는 KAN 이론에 따라 예측한 선을 빨간색 점선(α = k + 1 = 4)으로 표시하고 Sharma & Kaplan [17]에 따라 예측한 선을 검은색 점선(α)으로 표시합니다. = (k + 1)/d = 4/d). KAN은 더 가파른 빨간색 선을 거의 채울 수 있는 반면 MLP는 더 느린 검정색 선의 속도로 수렴하는 데 어려움을 겪고 빠르게 정체기에 도달합니다. 저자는 또한 마지막 예에서 2층 KAN이 3층 KAN(모양 [4, 2, 2, 1])보다 성능이 훨씬 나쁘다는 점에 주목합니다. 이는 더 깊은 KAN이 더 표현력이 뛰어나고 MLP의 경우에도 마찬가지라는 점을 강조합니다. 더 깊은 MLP가 얕은 MLP보다 더 표현력이 좋습니다.

특수 기능

이 섹션에서는 다음 두 가지 사항을 보여줍니다.

(1) Kolmogorov의 관점에서 밝혀진 특수 기능의 (대략) 컴팩트 KA 표현을 찾는 것이 가능합니다. Arnold 표현 특수 기능의 새로운 수학적 속성.

(2) KAN은 특수 기능을 표현하는데 있어서 MLP보다 더 효율적이고 정확합니다.

각 데이터 세트와 각 모델군(KAN 또는 MLP)에 대해 저자는 그림 3.2와 같이 매개변수 수와 RMSE 평면에 파레토 경계를 표시했습니다.

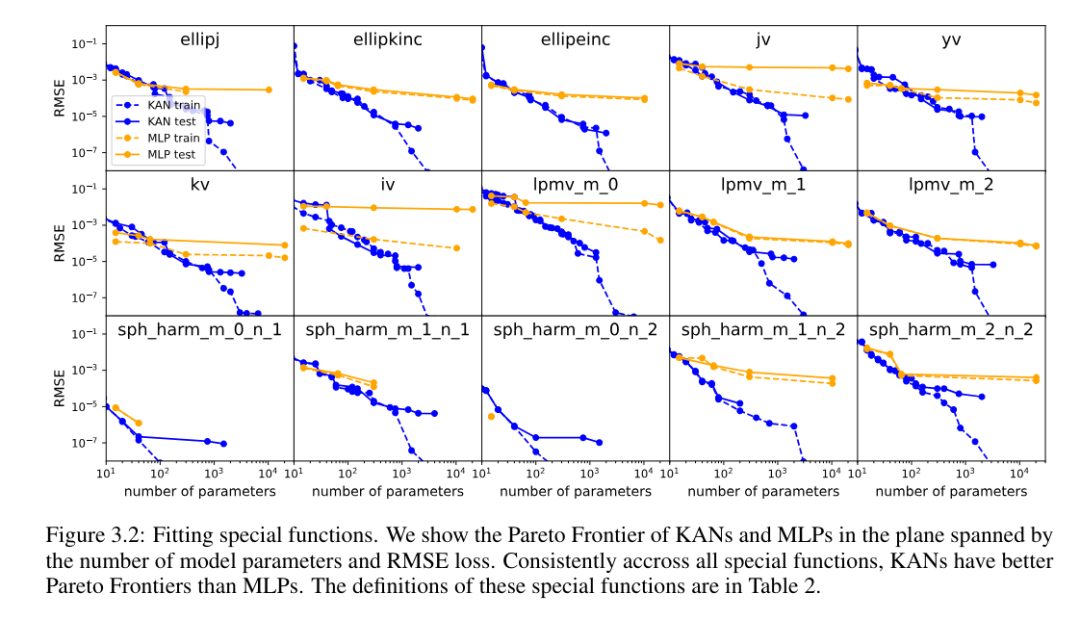
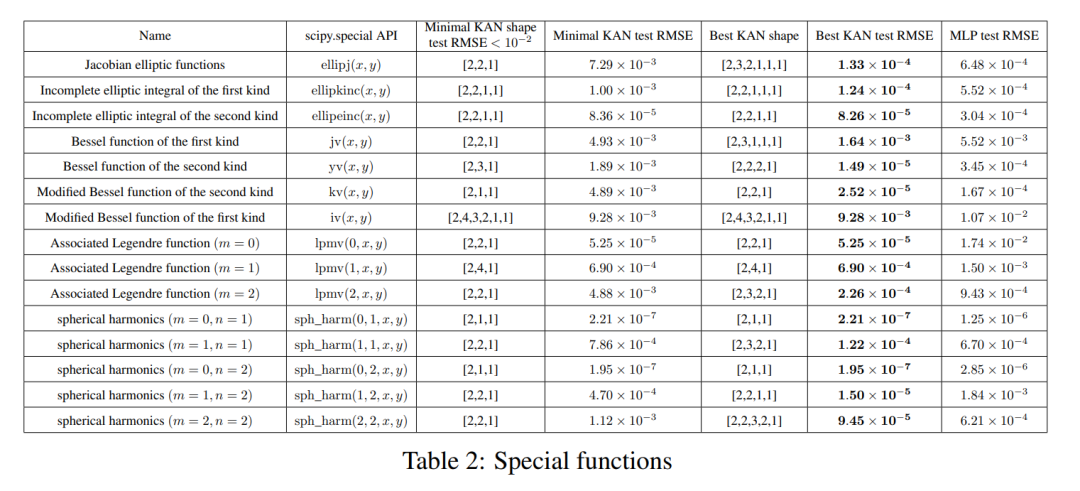
KAN은 지속적으로 MLP보다 더 나은 성능을 발휘합니다. 즉, 동일한 수의 매개변수를 사용하여 KAN은 MLP보다 더 낮은 훈련/테스트 손실을 달성할 수 있습니다. 또한 저자는 자동으로 발견한 특수 기능에 대한 KAN의 (놀랍도록 컴팩트한) 모양을 표 2에 보고합니다. 한편으로는 이러한 간결한 표현의 의미를 수학적으로 설명하는 것이 흥미롭습니다. 반면, 이러한 간결한 표현은 고차원 조회 테이블을 여러 개의 1차원 조회 테이블로 분해할 수 있음을 의미합니다. 이는 추론 시 일부 추가 작업을 수행하는 대신 많은 메모리를 절약할 수 있습니다(거의 무시할 수 있음) .

Feynman Dataset

이전 섹션의 설정은 우리가 "실제" KAN 모양을 명확하게 알고 있다는 것입니다. 이전 섹션의 설정은 우리가 "실제" KAN 모양을 분명히 모른다는 것입니다. 이 섹션에서는 중간 설정을 연구합니다. 데이터 세트의 구조를 고려할 때 KAN을 수동으로 구축할 수 있지만 이것이 최적인지는 확실하지 않습니다.

각 초매개변수 조합에 대해 저자는 3개의 무작위 시드를 시도했습니다. 각 데이터 세트(방정식) 및 각 방법에 대해 무작위 시드 및 깊이에서 최상의 모델(최소 KAN 모양 또는 가장 낮은 테스트 손실)의 결과를 표 3에 보고합니다.

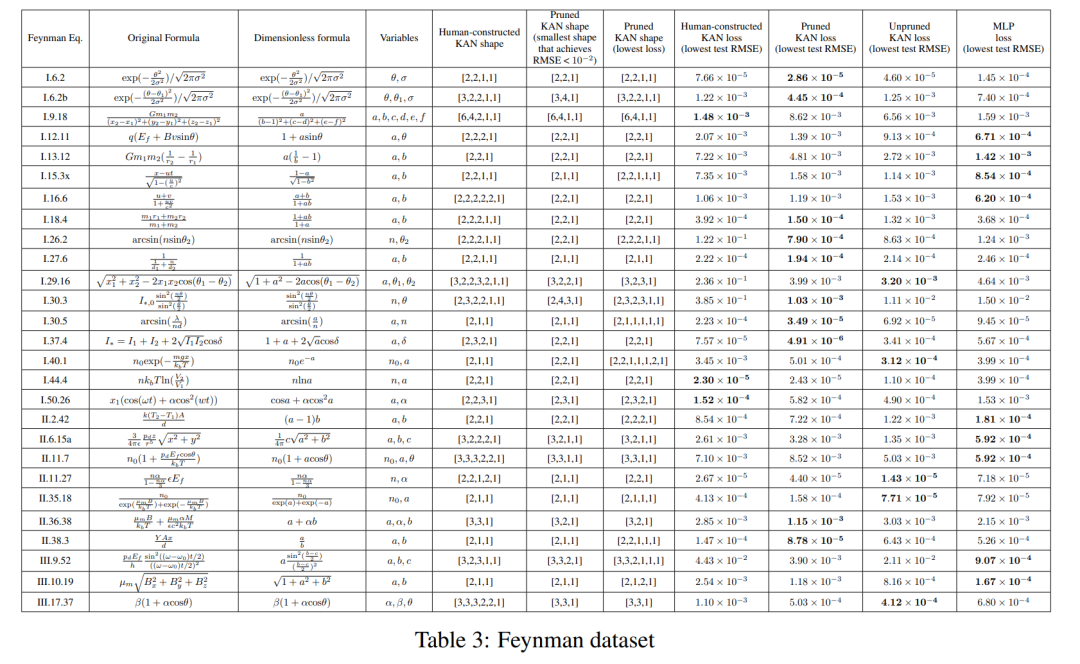
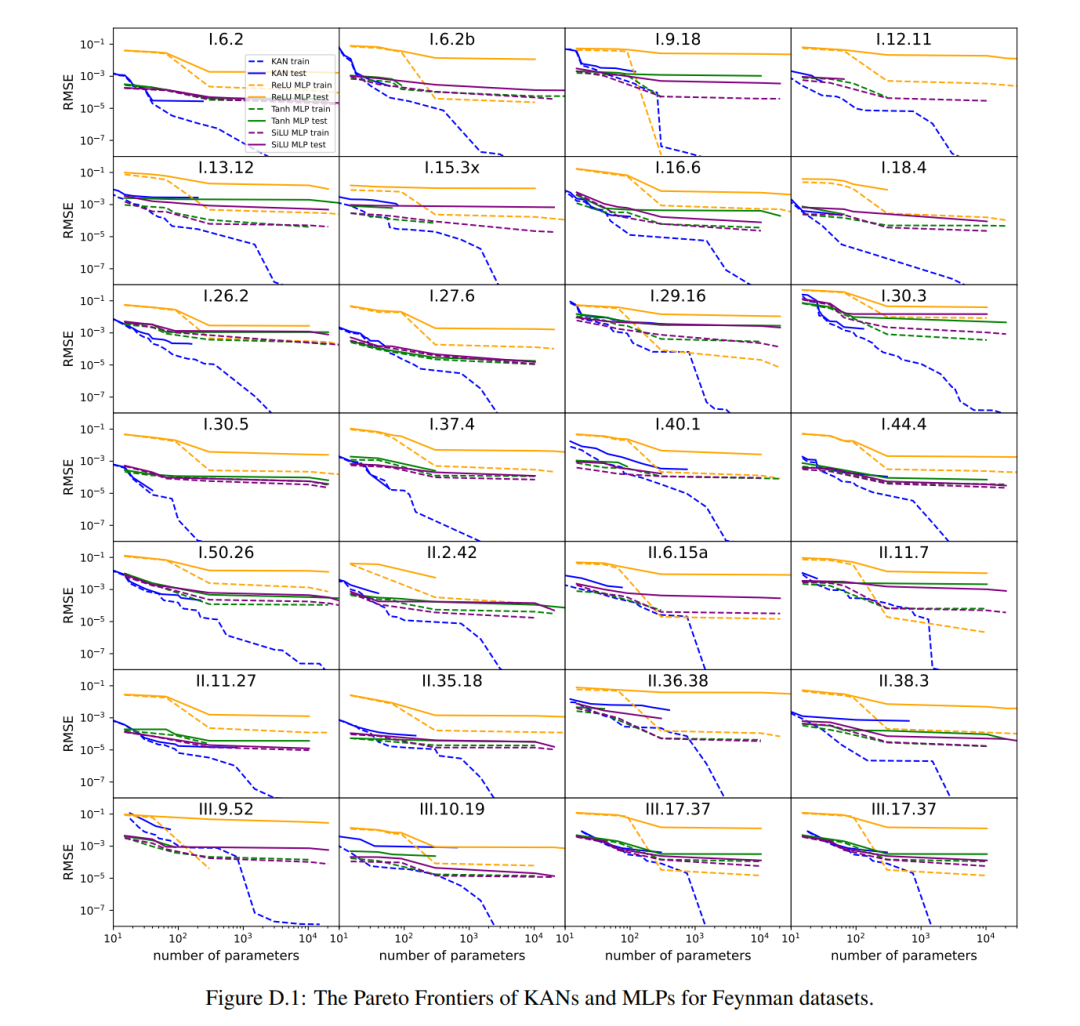
그들은 MLP와 KAN이 평균적으로 똑같이 좋은 성능을 발휘한다는 것을 발견했습니다. 각 데이터세트와 각 모델군(KAN 또는 MLP)에 대해 저자는 그림 D.1과 같이 매개변수 수와 RMSE 손실로 구성된 평면에 파레토 경계를 표시했습니다. 그들은 Feynman 데이터 세트가 KAN에 의한 추가 개선을 허용하기에는 너무 단순하다고 추측합니다. 이는 종종 진동 동작을 나타내는 특수 기능의 복잡성과 달리 변수 종속성이 종종 매끄럽거나 단조롭다는 의미입니다.

편미분 방정식 풀기

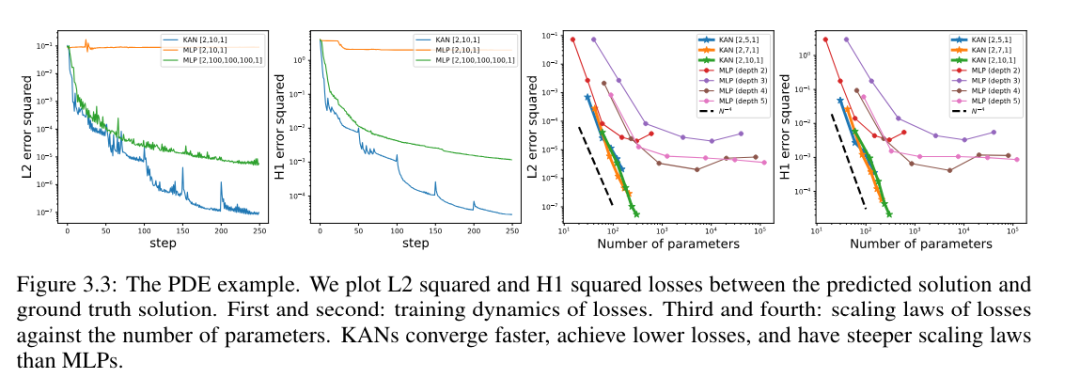
저자는 동일한 하이퍼파라미터를 사용하여 KAN과 MLP 아키텍처를 비교했습니다. 그들은 L^2 표준과 에너지(H^1) 표준에서 오류를 측정하고 KAN이 더 작은 네트워크와 더 적은 매개변수를 사용하면서 더 나은 스케일링 법칙과 더 작은 오류를 달성했음을 관찰했습니다(그림 3.3 참조). 따라서 그들은 KAN이 편미분 방정식(PDE) 모델 축소를 위한 좋은 신경망 표현 역할을 할 수 있는 잠재력을 가질 수 있다고 추측했습니다.

지속 학습

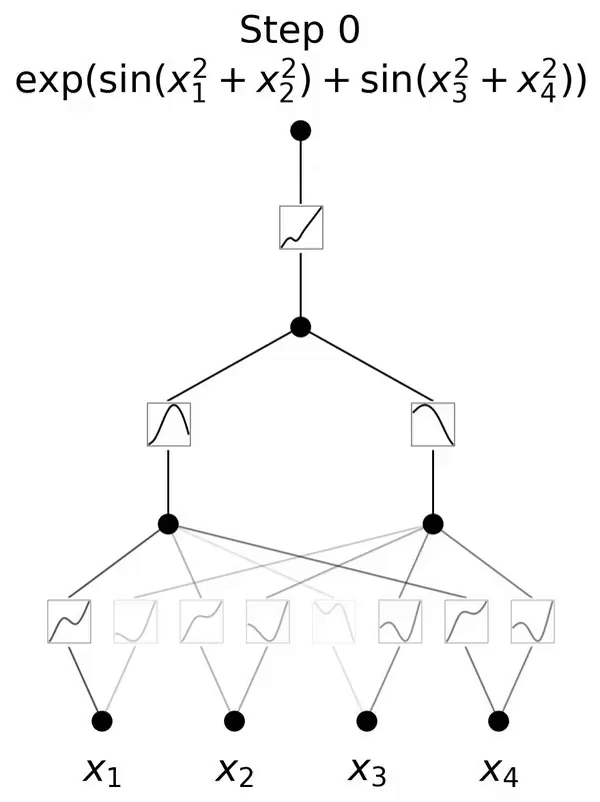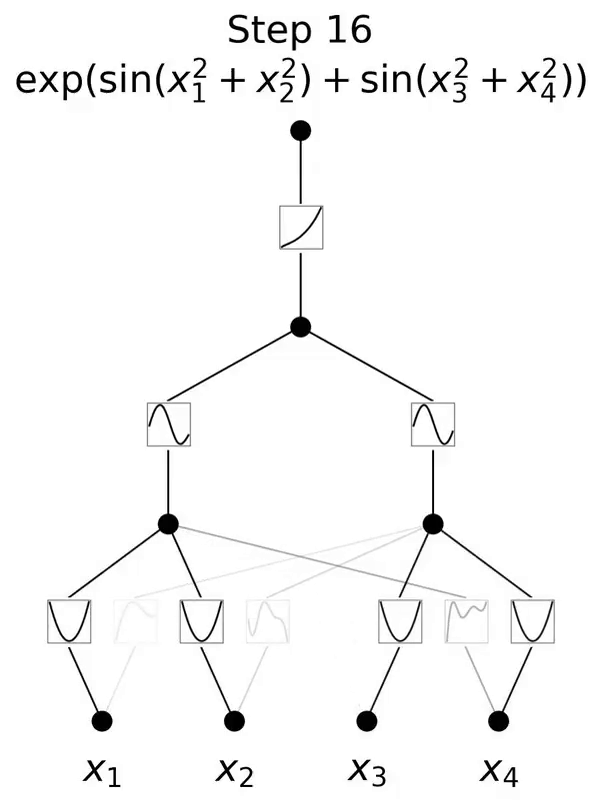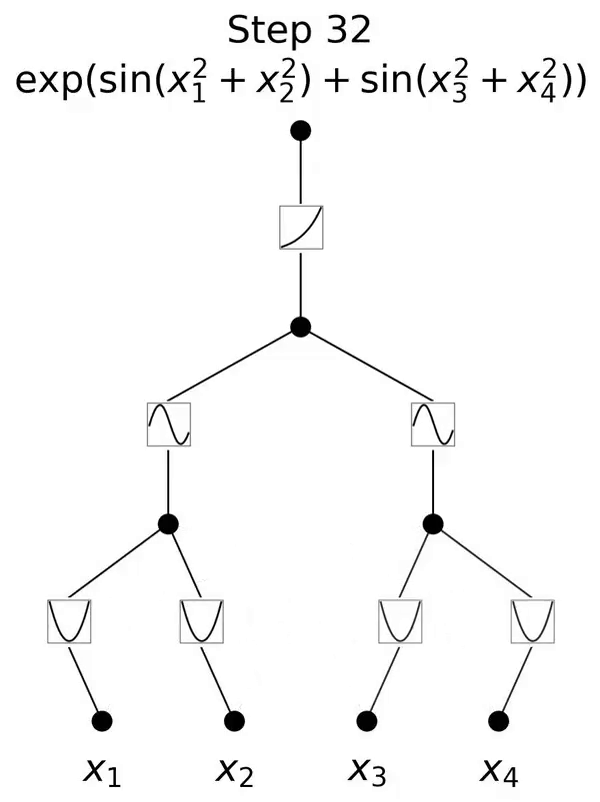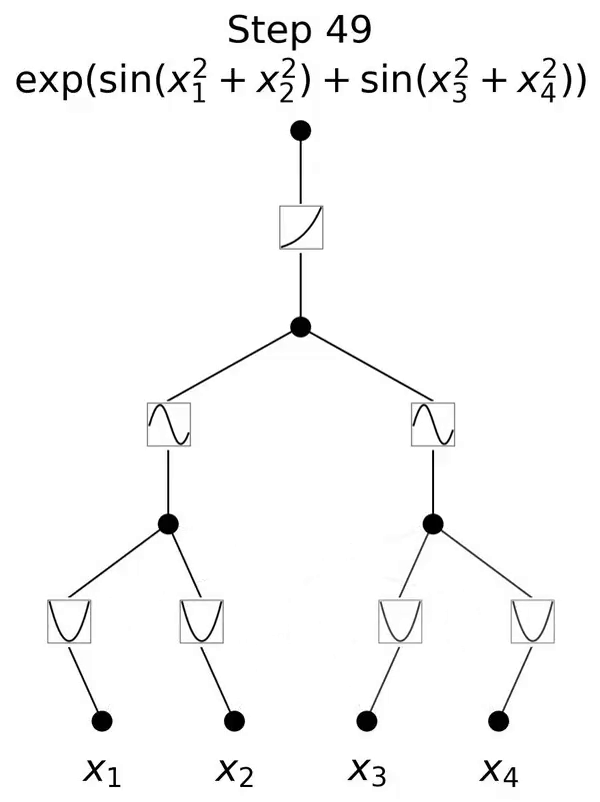
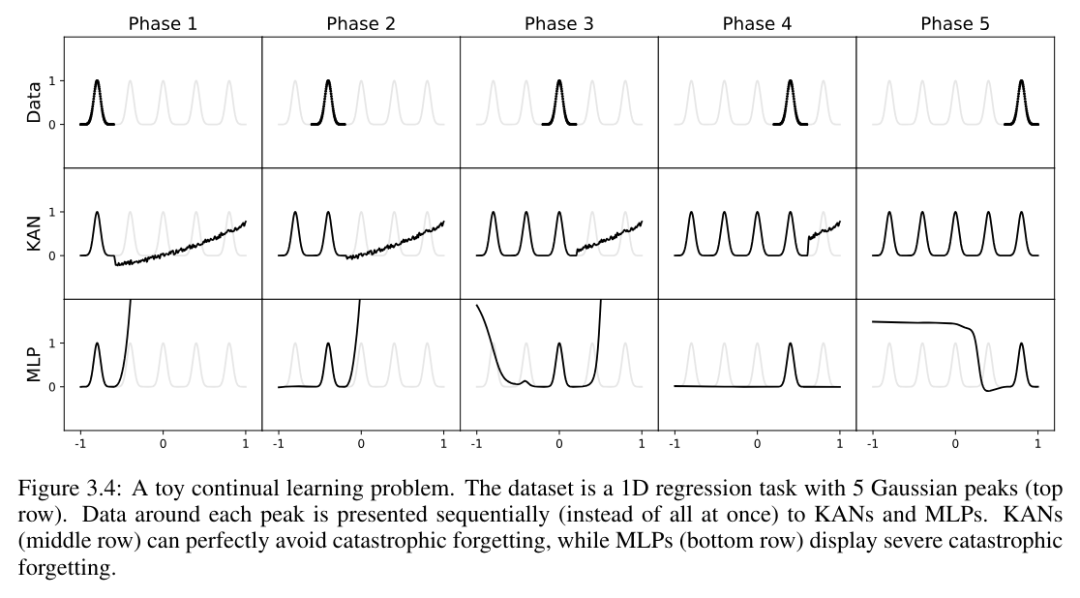
저자는 KAN이 국소 가소성을 가지며 스플라인의 국소성을 활용하여 치명적인 망각을 피할 수 있음을 보여줍니다. 아이디어는 간단합니다. 스플라인 기반이 로컬이기 때문에 샘플은 가까운 몇 개의 스플라인 계수에만 영향을 미치고 먼 계수는 변경되지 않은 채 유지됩니다. (이것은 먼 영역이 우리가 원하는 정보를 유지하려는 계수를 먼 영역에 이미 저장할 수 있기 때문에 우리가 원하는 것입니다.) . 대조적으로, MLP는 일반적으로 ReLU/Tanh/SiLU 등과 같은 전역 활성화 함수를 사용하기 때문에 로컬 변경 사항이 제어할 수 없을 정도로 먼 지역으로 전파되어 그곳에 저장된 정보가 파괴될 수 있습니다.

저자는 이러한 직관을 검증하기 위해 간단한 예를 사용합니다. 1차원 회귀 작업은 5개의 가우스 피크로 구성됩니다. 그림 3.4의 맨 윗줄에 표시된 것처럼 각 피크 주변의 데이터는 순차적으로(한 번에 모두가 아닌) 표시되며 KAN과 MLP에 별도로 표시됩니다. 각 훈련 단계 이후 KAN과 MLP의 예측 결과는 각각 중간 행과 아래쪽 행에 표시됩니다. 예상한 대로 KAN은 현재 단계에서 데이터가 존재하는 영역만 재구성하고 이전 영역은 변경되지 않습니다. 대조적으로, MLP는 새로운 데이터 샘플을 본 후 전체 영역을 재구성하므로 치명적인 망각으로 이어집니다.

KAN은 해석 가능합니다.

이 기사의 4장에서 저자는 섹션 2.5에서 개발된 기술 덕분에 KAN이 해석 가능하고 대화형임을 보여줍니다. 그들은 합성 작업(섹션 4.1 및 4.2)뿐만 아니라 실제 과학 연구에서도 KAN의 적용을 테스트하고 싶었습니다. 그들은 KAN이 접합 이론(섹션 4.3)과 응집 물질 물리학(섹션 4.4)의 상 전이 경계에서 복잡한 관계를 (재)발견할 수 있음을 보여줍니다. 정확성과 해석 가능성으로 인해 KAN은 AI + 과학의 기본 모델이 될 가능성이 있습니다.

토론

논문에서 저자는 KAN의 한계와 향후 개발 방향을 수학적 기초, 알고리즘 및 응용의 관점에서 논의합니다.

수학적 측면: 저자가 KAN(정리 2.1)에 대한 예비 수학적 분석을 수행했지만 수학적 이해는 여전히 매우 제한적입니다. Kolmogorov-Arnold 표현 정리는 수학적으로 철저하게 연구되었지만 이는 KAN의 매우 제한된 하위 클래스인 [n, 2n + 1, 1] 모양의 KAN에 해당합니다. 더 깊은 KAN에 대한 경험적 성공이 수학적으로 근본적인 것을 의미합니까? 매력적으로 일반화된 Kolmogorov-Arnold 정리는 두 레이어의 조합을 넘어 "더 깊은" Kolmogorov-Arnold 표현을 정의할 수 있으며 잠재적으로 활성화 함수의 부드러움을 깊이와 연관시킬 수 있습니다. 원래(깊이 2) Kolmogorov-Arnold 표현에서는 원활하게 표현할 수 없지만 깊이 3 이상에서는 원활하게 표현할 수 있는 함수가 있다고 가정합니다. 함수 클래스를 특성화하기 위해 "Kolmogorov-Arnold 깊이" 개념을 사용할 수 있습니까?

알고리즘 측면에서 그들은 다음 사항에 대해 논의했습니다:

정확성. 아키텍처 설계 및 교육에는 완전히 조사되지 않은 여러 옵션이 있으므로 정확성을 더욱 향상시킬 수 있는 대안이 있을 수 있습니다. 예를 들어 스플라인 활성화 함수는 방사형 기준 함수나 기타 로컬 커널 함수로 대체될 수 있습니다. 적응형 그리드 전략을 사용할 수 있습니다.

효율성. KAN이 느린 주된 이유 중 하나는 서로 다른 활성화 함수가 일괄 계산(동일한 함수를 통해 전달되는 대량의 데이터)을 활용할 수 없기 때문입니다. 실제로 활성화 함수를 그룹("다중")으로 그룹화하여 MLP(모든 활성화 함수가 동일함)와 KAN(모든 활성화 함수가 다름) 사이를 보간할 수 있습니다. 여기서 그룹의 구성원은 동일한 활성화 함수를 공유합니다.

KAN과 MLP의 혼합. MLP와 비교하여 KAN에는 두 가지 주요 차이점이 있습니다.

• (i) 활성화 함수는 노드 대신 가장자리에 있습니다.

• (ii) 활성화 함수는 고정된 대신 학습 가능합니다.

KAN의 장점을 더 잘 설명하는 변화는 무엇인가요? 저자는 부록 B에 예비 결과를 제시합니다. 여기서는 (ii)를 사용하여 모델을 연구합니다. 즉, 활성화 함수는 학습 가능하지만(KAN과 같이), (i)가 없으면 활성화 함수가 노드에 위치합니다(MLP와 유사). ). 또한 활성화 함수가 MLP와 같이 고정되어 있지만 KAN과 같이 가장자리에 위치한 또 다른 모델을 구축할 수 있습니다.

적응성. 스플라인 기반 기능의 고유한 지역성으로 인해 KAN의 설계 및 교육에 적응성을 도입하여 정확성과 효율성을 향상시킬 수 있습니다. 멀티그리드 방법이나 도메인 종속 기반 기능과 같은 다단계 교육 아이디어는 [93, 94]를 참조하세요. [95]의 다중 스케일 방법과 같습니다.

응용 프로그램: 저자는 물리 방정식 피팅 및 PDE 해결과 같은 과학 관련 작업에서 KAN이 MLP보다 더 효과적이라는 몇 가지 예비 증거를 제시했습니다. 그들은 KAN이 Navier-Stokes 방정식, 밀도 범함수 이론 또는 회귀 분석이나 PDE 솔루션으로 공식화될 수 있는 기타 작업을 해결하는 데에도 유망할 수 있다고 예상합니다. 또한 그들은 KAN을 변환기와 같은 현재 아키텍처에 통합해야 하는 기계 학습 관련 작업에 KAN을 적용하기를 희망합니다. 변환기에서 MLP를 KAN으로 대체하기 위해 "kansformer"를 제안할 수 있습니다.

AI + 과학을 위한 언어 모델인 KAN: 대규모 언어 모델은 자연어를 사용할 수 있는 누구에게나 유용하기 때문에 혁신적입니다. 과학의 언어는 함수이다. KAN은 해석 가능한 기능으로 구성되어 있으므로 인간 사용자가 KAN을 응시하면 기능적 언어를 사용하여 KAN과 통신하는 것과 같습니다. 이 단락은 특정 도구 KAN보다는 AI-과학자 협업 패러다임을 강조하기 위한 것입니다. 사람들이 의사소통을 위해 서로 다른 언어를 사용하는 것처럼 저자는 미래에 KAN이 AI + 과학의 언어 중 하나일 뿐일 것이라고 예측합니다. 의사소통하다. 그러나 KAN의 활성화 덕분에 AI-과학자 협업 패러다임이 그 어느 때보다 쉽고 편리해졌으며 AI + 과학에 어떻게 접근하고 싶은지 다시 생각하게 되었습니다. 우리는 AI 과학자를 원하는가, 아니면 과학자를 돕는 AI를 원하는가? (완전 자동화된) AI 분야의 과학자들에게 내재된 어려움은 인간 선호도를 AI 목표로 성문화하는 인간 선호도를 정량화하는 것이 어렵다는 것입니다. 실제로 어떤 기능이 단순하거나 해석 가능한지에 대해 분야마다 과학자마다 감정이 다를 수 있습니다. 따라서 과학자들은 과학의 언어(기능)를 구사할 수 있고, 특정 과학 영역에 맞게 개별 과학자의 귀납적 편견과 쉽게 상호작용할 수 있는 AI를 보유하는 것이 바람직하다.

주요 질문: KAN 또는 MLP?

현재 KAN의 가장 큰 병목 현상은 느린 훈련 속도입니다. 동일한 수의 매개변수를 사용하면 KAN의 학습 시간은 일반적으로 MLP의 10배입니다. 저자들은 솔직히 말해서 KAN의 효율성을 최적화하기 위한 노력을 하지 않았기 때문에 KAN의 느린 훈련 속도를 근본적인 한계라기보다는 앞으로 개선할 수 있는 공학적 문제로 본다고 말합니다. 누군가 모델을 빠르게 훈련시키고 싶다면 MLP를 사용해야 합니다. 그러나 다른 경우에는 KAN이 MLP만큼 좋거나 더 좋아 시도해 볼 가치가 있습니다. 그림 6.1의 의사결정 트리는 KAN을 언제 사용할지 결정하는 데 도움이 될 수 있습니다. 간단히 말하면 해석 가능성 및/또는 정확성에 관심이 있고 느린 학습이 큰 문제가 되지 않는다면 저자는 KAN을 사용해 볼 것을 권장합니다.

자세한 내용은 원문을 읽어주세요.

위 내용은 Transformer가 Kansformer가 되고 싶나요? 도전자 KAN을 안내하는 데 수십 년을 보낸 MLP의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!