소형 모델의 성능이 포화 상태이고 성능이 좋지 않은 근본 원인은 Softmax입니까?

작은 언어 모델의 등장은 큰 언어 모델의 비용이 많이 드는 훈련과 추론의 단점을 보완하기 위한 것이지만, 일정 단계까지 훈련한 후에는 성능이 저하되는(포화 현상) 점도 있기 때문에 그 이유는 다음과 같습니다. 이 현상은 무엇입니까? 작은 언어 모델의 성능을 향상시키기 위해 극복하고 활용할 수 있습니까?

언어 모델링 분야의 최신 발전은 매우 큰 규모의 웹 텍스트 말뭉치에서 고도로 매개변수화된 신경망을 사전 훈련시키는 데 있습니다. 실제로 이러한 모델을 훈련 및 추론에 사용하는 것은 비용이 많이 들 수 있으므로 더 작은 대체 모델을 사용해야 합니다. 그러나 더 작은 모델은 포화 및 일부 고급 훈련 단계에서 능력 감소 및 정체 현상을 겪는 현상이 발생할 수 있다는 것이 관찰되었습니다.

최근 논문에서는 이러한 포화 합 현상이 더 작은 모델의 잠재 차원과 대상 컨텍스트 확률 분포의 높은 순위 간의 불일치로 설명될 수 있음을 발견했습니다. 이러한 불일치는 소프트맥스 병목 현상을 사용하여 이러한 모델에 사용되는 선형 예측 헤드의 성능에 영향을 미칩니다.

문서 링크: https://arxiv.org/pdf/2404.07647.pdf

이 문서는 다양한 설정에서 소프트맥스 병목 현상의 영향을 측정하고 1000개 미만의 숨겨진 차원을 기반으로 하는 모델이 사전에 발생하는 경향이 있음을 발견했습니다. - 훈련된 Degenerate 잠재 표현은 이후 단계에서 채택되어 평가 성능이 저하됩니다.

소개

표현 저하 문제는 텍스트 데이터의 자기 지도 학습 방법과 같은 다양한 모드에 영향을 미치는 일반적인 현상입니다. 언어 모델의 중간 표현을 관찰하면 낮은 각도의 가변성(또는 이방성) 또는 훈련 중에 발생하는 비정상적인 차원이 드러납니다. 그러나 이러한 관찰은 대부분 BERT 또는 GPT-2와 같은 계열 모델과 비교할 수 있는 차원을 가진 상대적으로 작은 규모의 모델에서 이루어집니다.

이 모델은 일반적으로 일련의 토큰

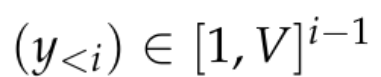
을 받아들이고 R^d에서 상대적으로 낮은 차원의 컨텍스트 표현을 생성하는 신경망 f_θ로 구성됩니다. 여기서 d는 모델의 숨겨진 차원입니다. 그런 다음 컨텍스트 토큰 확률의 로그를 생성하는 언어 모델링 헤드에 의존합니다. 언어 모델링 헤드에 대한 일반적인 선택은 매개변수 W ∈ R^(V×d)가 있는 선형 레이어입니다. 여기서 V는 가능한 토큰 수입니다. 따라서 다음 토큰에 대한 결과 확률 분포는 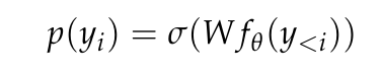여기서 σ는 소프트맥스 함수입니다.

언어 모델링 분야에서는 GPT-2에서 도입한 생성적 사전 학습 방법을 확장하는 것이 현재 추세입니다. 이는 거대한 웹 텍스트 모음에서 수십억 개의 매개변수로 구성된 신경 모델을 학습하는 것을 의미합니다. 그러나 이러한 고도로 매개변수화된 모델을 교육하고 적용하면 에너지 및 하드웨어 관련 문제가 발생하므로 더 작은 모델로 유사한 성능 수준을 달성할 수 있는 방법을 찾아야 합니다.

그러나 Pythia 모델 제품군의 평가에 따르면 매우 큰 말뭉치에서 작은 모델을 훈련하면 사전 훈련 후반에 성능 저하로 나타나는 포화 상태가 발생할 수 있습니다. 이 논문은 표현 저하의 렌즈를 통해 이러한 포화 현상을 탐구하고 두 현상 사이에 강한 상관 관계가 있음을 발견하는 동시에 표현 저하가 작은 모델의 언어 모델링 헤드에서 발생하며 이론적으로나 경험적으로 입증되었습니다. 선형 언어 모델링 헤더가 작은 숨겨진 차원을 기반으로 하는 아키텍처의 성능 병목 현상이 될 수 있는 방법을 보여줍니다.

언어 모델 포화 현상

이 문서는 먼저 Pythia 체크포인트의 성능 포화가 실제로 관찰되고 정량화될 수 있음을 검증합니다. 왜냐하면 Pythia 체크포인트는 다양한 모델 크기에 대해 유일하게 게시된 중간 체크포인트이기 때문입니다. 이 논문은 사전 훈련 데이터 세트(즉, The Pile)에서 무작위로 샘플링된 50,000개의 토큰에 대한 Pythia 체크포인트의 교차 엔트로피를 측정합니다.

그림 1a에서 4억 1천만 개의 매개변수 모델조차도 고급 훈련 단계에서 도메인 손실이 증가하여 포화 상태에 직면한다는 것을 분명히 볼 수 있습니다.

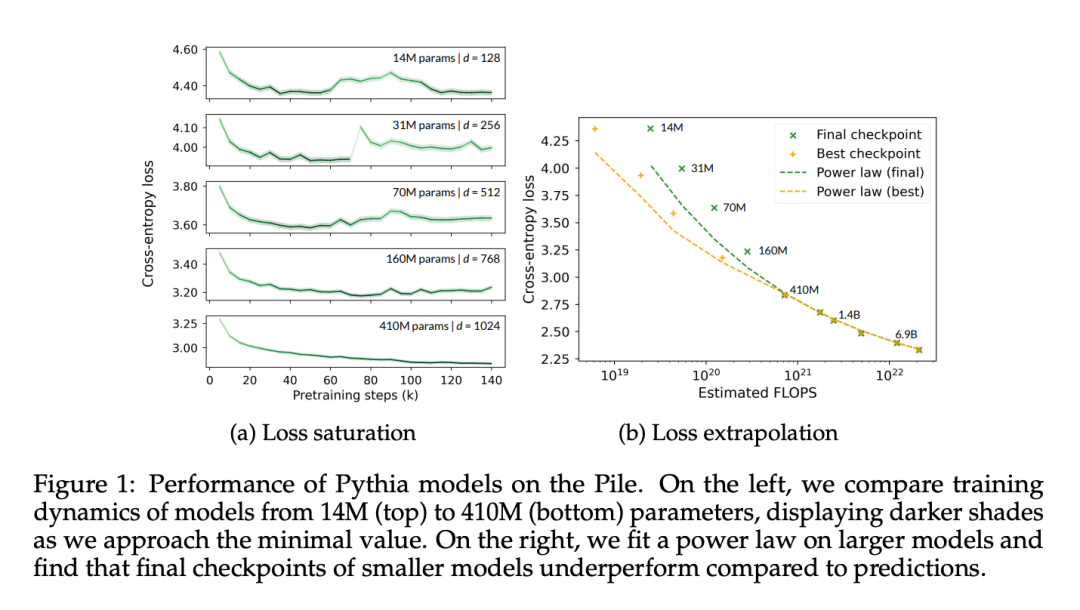
그림 1b에서 이 기사는 Hoffmann et al.(2022)의 방법에 따라 4억 1천만 개의 매개변수부터 시작하여 모델의 데이터 포인트를 맞추고 모델과 관련된 상수(A 및 α)만 최적화합니다. , 다른 모든 값을 재사용하는 동안 (B = 410.7, β = 0.28, E = 1.69). 여기서는 Hoffmann et al(2022)이 제시한 매개변수 개수 N과 토큰 개수 T 사이의 관계를 검토합니다.

이 논문에서는 최적의 매개변수가 A = 119.09, α = 0.246인 것으로 나타났습니다. 저자는 최적 및 최종 체크포인트에 해당하는 토큰 수의 적합 곡선을 보여줍니다. 최종 체크포인트의 성능은 추정값보다 평균 약 8% 정도 낮은 것을 확인할 수 있습니다. 손실 최소화(최적) 체크포인트는 학습률 냉각이 불완전하여 외삽법보다 낮을 것으로 예상되었으나, 외삽법에 비해 성능이 약 4% 정도 낮을 뿐이었다.

언어 모델 평가 도구(LM Evaluation Harness)의 평가에 사용된 데이터 세트에서도 유사한 성능 포화 현상이 관찰되었으며, 표 1과 같습니다.

성능 포화는 순위 포화입니다.

규모 이방성

이방성은 다양한 소규모 언어 모델에서 관찰되는 표현 저하의 일반적인 형태입니다. 이는 특정 언어 모델에서 표현 분포의 각도 가변성의 감소를 포함합니다. 층. 이전 연구(Ethayarajh, 2019; Godey et al., 2024)는 작은 변형된 언어 모델의 거의 모든 레이어가 이방성이라는 점을 지적했습니다. 벡터 표현 세트 H에서 이방성을 측정하는 일반적인 방법은 평균 코사인 유사성입니다.

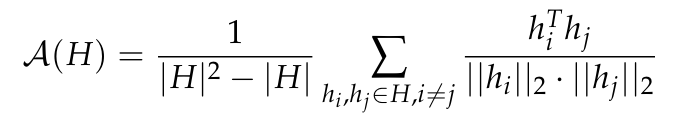
그러나 이방성이 10억 개가 넘는 매개변수가 있는 모델에 영향을 미치는지는 확실하지 않습니다. 이 문제를 해결하기 위해 이 논문에서는 일련의 모델 중간 표현, 즉 GPT-2, OPT, Pythia 및 Gemma에 대한 레이어 간의 평균 코사인 유사성을 계산합니다. 이 문서에서는 이 데이터 세트의 도메인이 이러한 제품군에 사용된 사전 훈련된 데이터 세트의 도메인을 포함하거나 일치한다고 가정하기 때문에 The Pile의 하위 샘플을 사용합니다.

그림 2에서는 대부분의 Transformer 모델의 대부분 레이어가 규모에 관계없이 어느 정도 이방성임을 확인할 수 있습니다. 그러나 마지막 레이어에는 모델이 거의 등방성이거나 고도로 이방성인 이분법이 있는 것으로 보입니다. 이 논문에서는 이 이분법이 1억 6천만 개 이하의 매개변수를 가진 모델만 마지막 레이어의 이방성에 영향을 받는 Pythia 제품군의 포화 현상 중 하나와 일치한다고 지적합니다.

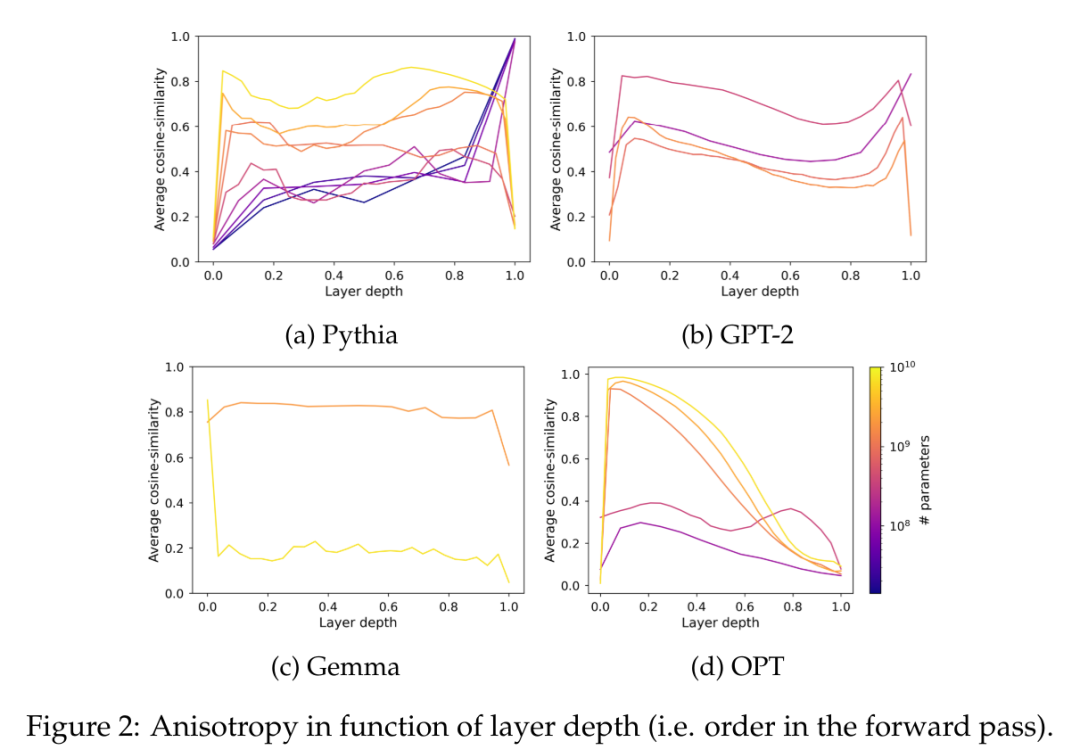
이 기사에서는 Pythia 제품군의 이방성 훈련 역학을 연구하고 이를 그림 3의 포화 현상과 비교합니다.

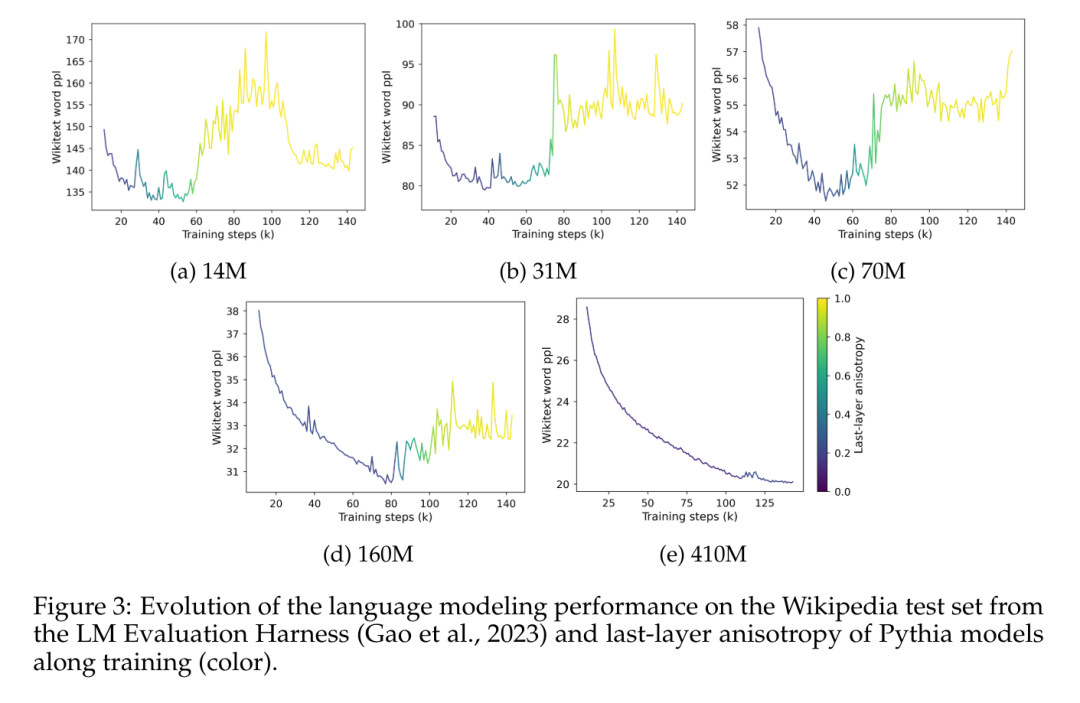
그림 3은 모델의 마지막 레이어 표현에서 성능 포화의 출현과 이방성의 출현 사이의 명확한 상관관계를 명확하게 보여줍니다. 또한 훈련 중 포화점 근처에서 이방성이 갑자기 증가하는 것을 보여줍니다. 여기서 관찰되는 것은 특정 도메인 내 코퍼스 내에서 모델이 포화 시 성능을 빠르게 잃고 이러한 폭발로부터 완전히 회복되지 않는 것 같습니다.

특이값 포화

평균 코사인 유사성은 분포 균일성에 대한 중요한 척도이지만, 다른 측정항목을 포함하면 특정 다양체의 복잡성을 더 잘 포착하는 데 도움이 될 수 있습니다. 또한 가중치가 아닌 언어 모델의 출력 임베딩에만 중점을 둡니다. 이 섹션에서는 경험적 관찰을 본 논문의 이론적 결과와 연결하기 위해 언어 모델링 헤드의 특이값 분포를 연구하여 본 논문의 분석을 확장합니다.

그림 4는 훈련 중 최종 예측 레이어 가중치 W에 따른 특이값 분포를 보여줍니다.

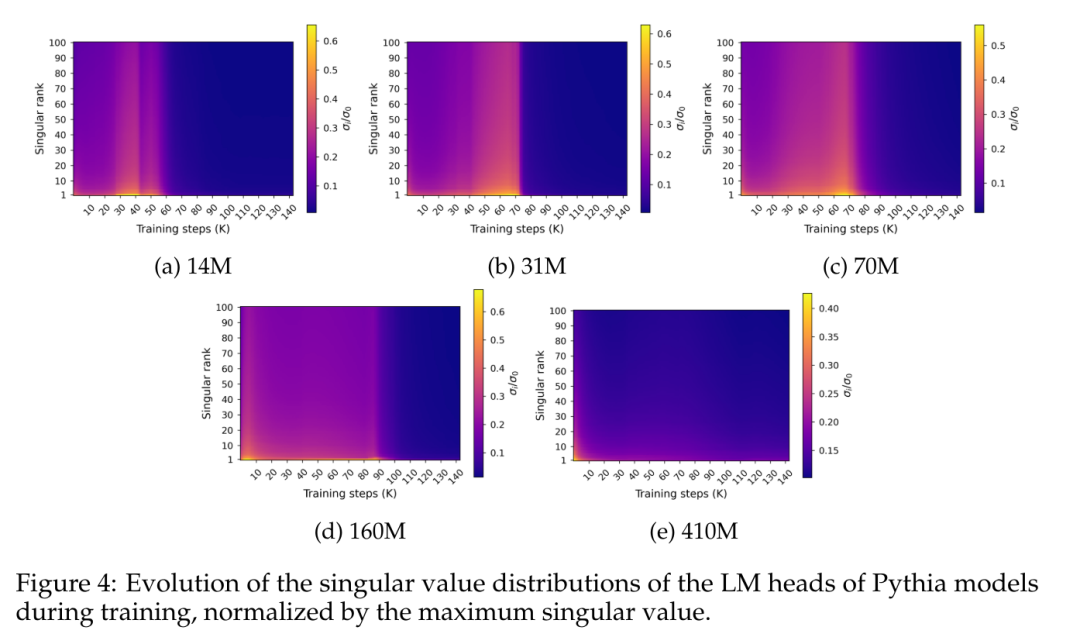
그림 4는 성능 포화와 거의 동시에 발생하는 스펙트럼 포화의 특정 패턴을 보여줍니다. 그림을 보면 특이값 분포가 훈련 과정에서 점차 평탄화되어 거의 균일성에 도달한 다음 갑자기 다른 분포에 비해 상대적으로 가장 큰 특이값이 높은 뾰족한 분포로 진화하는 것을 보여줍니다.

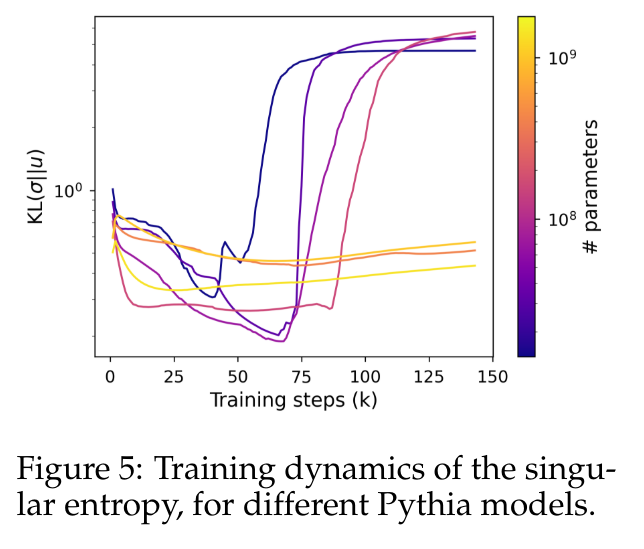
이 동작을 더 정확하게 수량화하기 위해 이 문서에서는 정규화된 특이값 분포와 균일 분포 간의 Kullback-Leibler 발산으로 계산된 특이 엔트로피 측정법을 사용합니다.

그림 5는 더 큰 매개변수를 사용하는 모델과 비교하여 4억 1천만 개 미만의 매개변수를 사용하는 모델의 특이 분포가 어떻게 다르게 전개되는지 보여줍니다. 작은 모델의 헤드는 갑자기 성능이 저하될 때까지 특이값 분포가 점점 더 균일해지는 것을 확인하며 이는 언어 모델 성능 저하와 다시 연관됩니다. 더 큰 모델의 특이값 분포는 더 안정적인 경향이 있으며 훈련 전반에 걸쳐 명백한 단조로운 패턴을 나타내지 않습니다.

소프트맥스 병목 현상과 언어 차원

자연어의 본질적인 차원

직관적으로 말하면 위에서 관찰된 특이값 분포 포화 현상은 더 작은 모델에만 적용되며 이는 LM 헤드에 매우 중요합니다. 최적화에 관련된 질문을 받았습니다. 본 절에서는 LM 헤드 순위의 임계값을 실증적으로 측정하고 이 헤드의 출력이 일치해야 하는 상황별 확률 분포의 차원을 추정하는 방법을 제안합니다.

선형 헤드 순위의 영향을 경험적으로 측정하기 위해 이 논문에서는 고도로 매개변수화된 언어 모델에서 파생된 사전 훈련된 상황 표현에 대해 순위 제한 헤드를 훈련할 것을 제안합니다. 최대 순위 r을 제어하려면 W = AB ∈ R^(V×d) 형식의 헤드를 고려하십시오. 여기서 A ∈ R^(V×r) 및 B ∈ R^(r×d)의 계수는 다음에서 시작합니다. N(0 ,1)이 추출되었습니다(d는 모델의 숨겨진 차원임). 이 W 행렬의 순위는 매개변수 r ∈ [1, d]에 의해 제한된 값 범위에 걸쳐 스캔됩니다.

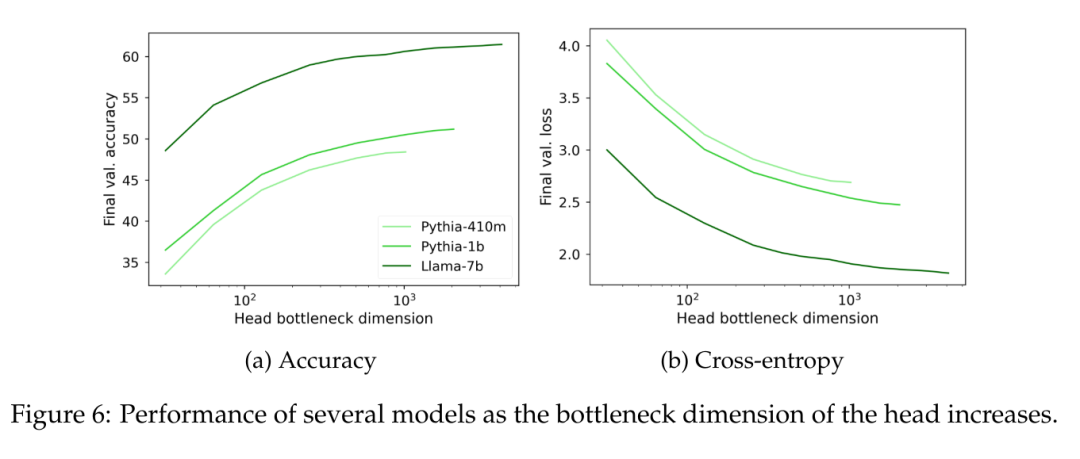
언어 모델을 동결하고 순위가 제한된 헤드를 약 1억 5천만 개의 토큰으로 훈련하는 동시에 학습 가능한 매개변수 수에 맞게 학습 속도를 조정합니다.

그림 6에서 볼 수 있듯이 모델 크기에 관계없이 언어 모델링 헤드 W의 순위가 1000 미만으로 떨어지면 Perplexity가 크게 감소하기 시작합니다. 이는 숨겨진 치수가 더 큰 모델의 경우 헤드가 주요 성능 병목 현상이 아니지만 숨겨진 치수가 더 작은 모델의 경우 출력 표현의 품질과 관계없이 성능이 저하될 수 있음을 의미합니다.

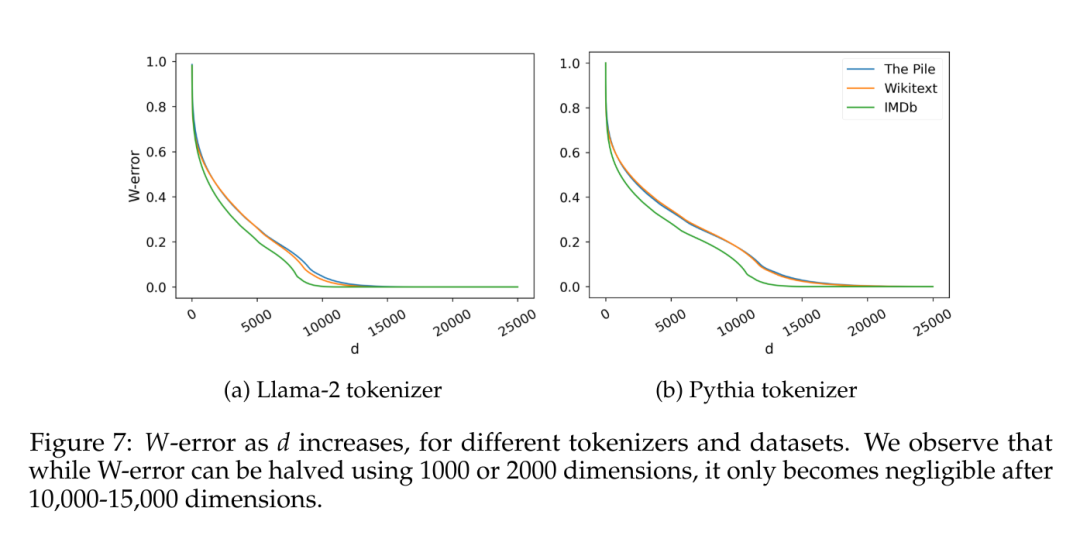
또 다른 흥미로운 요소는 추정 데이터 자체에 내재된 차원성입니다. 특정 귀납적 편향과 관련된 가능한 효과를 피하기 위해 이 문서에서는 두 가지 다른 어휘 크기(30,000개 토큰)를 사용하여 적용 범위가 다른 여러 데이터 세트(IMDb, Wikitext 및 The Pile)에 대해 순진한 5그램 언어 모델을 훈련했습니다. Llama-2, Pythia용 50,000개 토큰). C에서 관찰된 5그램이 주어지면 이 논문에서는 행렬 W ∈ R^(C×V)를 고려합니다. 여기서 각 행은 4개의 토큰이 주어진 가능한 토큰의 확률 분포이고 Terashima(2003)와 같은 특이값 분포를 계산합니다.

그림 7은 Eckart-Young-Mirsky 정리(Lemma 5.2 참조)에 의해 예측되고 W의 Frobenius 표준으로 정규화된 d 순위 행렬 W에 대한 최소 근사 오류인 W-오류를 보고합니다.

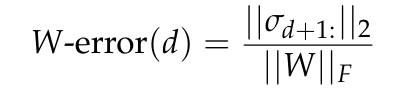
이론적 병목 현상

동시에 W의 추정 순위는 숨겨진 차원의 기존 크기 순서와 비교하여 무시할 수 없습니다. 여기서는 이상적인 선형 언어 모델링 헤드의 크기와 성능 간의 연관성을 이론적 관점에서 분석해 보겠습니다.

이 섹션의 목표는 컨텍스트 분포의 고유한 차원과 언어 모델 출력 표현의 낮은 차원으로 인해 발생할 수 있는 성능 병목 현상 사이의 공식적인 링크를 식별하는 것입니다. 이를 위해 이상적인 컨텍스트 표현에 최적화된 언어 모델링 헤드를 구상하고, 동일한 표현에 대해 하위 헤드를 훈련할 때 발생하는 스펙트럼 특성과 성능 격차 간의 관계를 탐색합니다.

자세한 연구 내용은 원본 논문을 확인하세요.

위 내용은 소형 모델의 성능이 포화 상태이고 성능이 좋지 않은 근본 원인은 Softmax입니까?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!